SHOLKOR типті параллельді платформалық манипуляторды жобалау: 8-параметрлік кинематикалық модельдеу және Даламбер теңдеулері негізіндегі динамикалық есептеулер


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:
КІРІСПЕ
Экономиканы қарқындату, оның өнімділігін арттыру ғылым мен техниканың жетілуіне негізделген қарқынды технологияларды қолданумен анықталады. Ғылыми-техникалық прогресті дамытудың негізгі бағыттарының бірі болып автоматталған машиналарды, робототехникалық кешендерді және есептеуіш техниканы қолдану негізінде технологиялық процесті автоматтандыру болып табылады.
Қазіргі кезде көптеген өндірістік операцияларды роботтар көмегімен орындайды. Олар өндірістің өнімділігін өнімдердің сапасын жоғарылату үшін арналған жабдықтар. Роботтардың қолдану аймақтары күннен күнге көбейіп жатыр. Былай айтқанда, өндірісте роботты қолдануы оның дамуын көрсетеді.
Робототехника өзі үлкен пән болып механиканы, автоматиканы компьютерлік техниканың басын қосып, күрделі есептерге әкеледі. Роботтар өткен ғасырдың 60-жылдары пайда болып қазіргі кезде оған мыңдаған зерттеу мақалалары шықты. Соның ішінде роботтардың динамикасыда қарқынды даму үстінде. Қозғалыс динамикасы теңдіктері негізінде манипуляторға әсер ететін күштер мен моменттерді математикалық түрде көрсету манипулятор динамикасының негізі болып табылады. Мұндай теңдеулер ЭЕМ көмегімен манипулятор қозғалысын модельдеу үшін, басқару заңын таңдау үшін және манипулятор құрылымы мен кинематикалық сұлбаның сапасын бағалау үшін қажет. Бұл жұмыста манипулятор динамикасының қозғалыс теңдеуін Даламбердің жалпыландырылған теңдеуі арқылы сипаттау қарастырылады.
Бірінші тарауда электрогидравликалық платформалық манипуляторды жобалау кезіндегі қолданылатын әдістердің қолданылуы қарастырылады.
Екінші тарауда жалпы робототехникалық жүйелер, оның кинематикасы мен динамикасы сипатталынады. Сонымен қатар бұл тарауда үзбелер мен буындардың, олардың координат жүйелерінің негізгі түсініктемелері келтіріледі.
Үшінші тарау динамиканың қозғалыс теңдеуін Даламбердің жалпыландырылған теңдеуі арқылы қарастырылады. Осының негізінде екі үзбелі манипулятордың қозғалыс динамикасын сипаттайтын жалпыландырылған теңдіктер жүйесі алынады.
Экономика бөлімінде роботтарды енгізу арқылы алынатын жылдық экономикалық тиімділік, өтелу мерзімі және жылдық экономия есептелінеді.
Еңбек қорғау бөлімінде роботтандырудың қауіпті және зиянды факторларына анализ жасалады. Және де пісіру роботтарын қолдану кезіндегі қорғану шараларын ұйымдастыру жағдайлары сипатталады.
Адамның тіршілік әрекетінің барлық сферасында мехатронды обьектілер, яғни қандай да бір мөлшерде электронды, электротехникалық және компьютерлік құраушылармен жабдықталған техника - қазіргі заманғы техникалық прогрестің ерекшелік белгісі болып табылады. Өндірісте осындай техникалардың мысалдары ретінде компьютерлік және сандық программалы басқарылатын қазіргі заманғы станоктар, өнеркәсіптік роботтар және басқа да технологиялық жабдық болып табылады.
- ТЕХНОЛОГИЯЛЫҚ БӨЛІМ
Сурет 1. 1-де SHOLKOR типті параллельді платформалық манипулятордың кинематикалық сұлбасы берілген. SHOLKOR типті параллельді манипупулятор 1 астыңғы платформадан және 2 жоғарғы платформадан тұрады, олардың нүктелері А1, В1, С1, А2, В2 кинематикалық цеппен 3 - 8 болып жалғанады. Жалғанатын кинематикалық цепте соңғы нүктелердің арасындағы арақашықтықты өзгертетін жетегі болады.
Ал шарлық аяқтаулар сфералық платформамен қосылу үшін қажет А1 А2 түйіндік нүктесіндегі бір ғана қосылатын кинематикалық цеппен (сәйкесінше 4 және 7 кинематикалық сфералық платформаны құрайды. Түйіндік нүктеде В1 сфералық платформамен қосылу 1 екі кинематикалық цепті құрайды 3 - 8 В2 нүктесінде 2 платформамен сфералық кинематикалық цеп 5 - 8 қосылады. А1 С1 түйіндік нүктесіндегі 1 платформамен сфералық кинематикалық парлар 4, 5, 6 кинематикалық цепті құрайды, ал С2 кинематикалық 3, 6, 7 цептер болады. Манипулятордың жұмыс істеу принципі мынаған негізделген: дененің кеңістегі жағдайын денеге тура жататын дене көмегімен және мына тураға жатпайтын дене нүктесімен болады. Тура қозғалысты В2 С2 мына жетектердің кинематикалық цепімен 3, 6, 7 және 5, 8 көмегімен іске асыруға болады. Ал келесіде берілген С2 нүктесі айналады, үш координатасын өзгерту кеңістегі кинематикалық цепті берілген координат арқылы анықтаймыз gi (i=1, 2, …, n) яғни кинематикалық жұпқа сәйкес айналу мінездемесіне байланысты болады. Яғни жұмыс органының жағдайын анықтау ушін кеңістікте мына координаталарды енгіземіз rj (i=1, 2, . . . , m) бұл жерде m = < 6. Жалпы жағдайда міндетті турде 6 скалярлы ұзындықтарды енгізу қажет, мысалы ұстағыш нүктесінің үш координатасын.
Сонымен бізге қажетті манипулятордың кинематикалық есебін қарастырамыз. Манипуляторды есептеу жолы арқылы кинематикалық цептің
ұзындығы 5, 6, 7 болады. Берілген координаттың 2 тура нүктесінде кинематикалық цептің ұзындығы 5, 8 болады және С1 В2, В1 В2 және С2 В1 сфералық қиылысу радиусы сияқты анықталады. Тура жағдайдың бағдарламасы А1 А2 ара қашықтығында анықталады. Параллельді манипуляторды шығару кезінде тура және кері есепті шығару барысында 8 параметрлі әдіс қолданылады мысалы SHOLKOR манипуляторы.
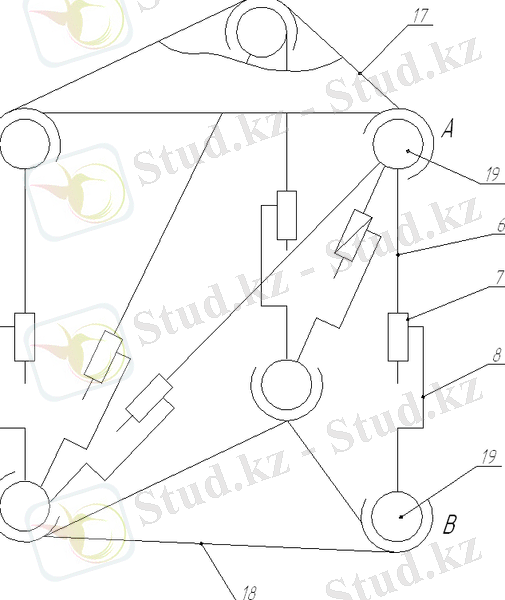
Сурет 1. 1 - Параллельді SHOLKOR типті платформалық манипулятордың кинематикплық сұлбасы
Бізге мәлім, робот механизмінің орындаушысында да шығу түйіні бірнеше кинематикалық цеппен байланысты, яғни олардың әрбіреуінде жетек болады, немесе шығу түйінінде бірнеше байланыс сандары болады. Бұл механизмнің параллельді структурасы немесе параллельді манипулятор деп аталады. Параллельді манипулятор мысалы SHOLKOR платформасы қаттылық жағынан көптеген артықшылығы бар, басқа манипулятормен салыстырғанда жуккөтергіштігімен өзгеше, бірақта бұл манипуляторлар тура және кері кинематикалық есептеу кезінде аналитикалық есептелуінің болуын ұстап қалады.
Бұл жерде параллельді манипуляторды кинематикалық модельдеуде, мысалы SHOLKOR платформасында матрицалық әдіс, 8 параметрлі қолданған дұрыс. ВСС құрылымдық топтарында декомпазицияны жіберетін және сондықтанда платформанын орналасу есебі анық түрде шешілетін жаңа құрылымды SHOLKOR платформасы беріледі. SHOLKOR платформасының нольдік ретті платформасы деп аталған орналасу туралы есептің шешімі үшін аса қажетті тұйықталудын алгебралық сызықты емес теңдеулердің санына байланысты. Нольдік ретті топтар әдісіне негізінде SHOLKOR платформаларынын барлық түрлерін кинематикалық зерттеуге жаңа жақындаулар ұсынылады. Әдіс бастапқы механизмнің реструктуризациясына (қайта құрылымдануында) бекітілген; бастапқы механизм қосымша тіреулер енгізу арқылы нольдік ретті платформаға дейін құралады. Қосымша тіреулердің ұзындықтары орналасу есебінін белгісу параметрлері болып табылады, ал нольдік ретті платформаға кірмейтін тіреудін ұзындықтары тұйықталу теңдеуінін оң жақ бөлігі болып табылады.
Есептелген орналасудын бастапқыдан үлкен алшақтығы кезінде SHOLKOR платформаларынын орналасу есебін шешуге тиімді әдіс жасау тапсырмасы қойылып, сәтті шешіледі. SHOLKOR- дын 5 - 3 және 6 - 6 платформалары үшін тұйықталу теңдеулері жазылған. 6 - 3 және басқа платформады құру кезінде қосымшалар қатарына кіретін тіреулердің біреуінін ұзындығынын өзгеруі кезіндегі нольдік ретті платформанын мүмкін болатын бір сәттік орын ауыстыруынын геометриясы зерттелген. Мүмкін болатын бір сәттік орын ауыстырудын негізінде жоғары жылдамдықты сәйкестілікпен Ньютон әдісі арқылы сызықты емес тұйықталу теңдеулерін шешуге қажетті туындынын мәні алынған.
SHOLKOR - дың 6 - 3 платформасынын орналасу есебін шешудің тиімді процедурасы құрылған. Есептелетін орналасудың бастапқыдан үлкен алшақтығы жағдайында процедуранын сәйкестілігі тексерілген:платформанын тік осьті 30°-пен айналуы; платформанын үштен бір және толық ұзындығы ретіндегі қашықтыққа орын ауыстырылады. Барлық шешілген есептерде 100 ретті тіреу ұзындығы, тіреу ұзындығының ретінің орын ауыстыруы және 1. 0Е-04 дәлдігі кезінде 3-тен 5 - ке дейін итерация қажет болады.
SHOLKOR - дың 6 - 6 платформасы үшін рекурсивті тәуелділіктің мүмкіндігі көрсетілген. Платформанын x және y бойымен (∆x=∆y=100) тіреу ұзындығынын ретінін шамасымен орын ауыстыру есебінін шешімі көрсетілген. 1. 0Е-04 дәлдік кезінде 11-12 (шығыс критерийіне байланысты) итерация қажет болады. Сәйкестілік жылдамдығынын жоғары, бірақ Ньютонның әдісіне қарағанда біраз төмендігі (рекурсивті тәуелділікті қолданғандықтан) анықталады. SHOLKOR - дың барлық 6 -N ретті (N=3, 4, 5) платформаларының орналасу есебінін шешімі анализденеді. Нольдік ретті топ әдісі негізінде көрсетілген реттілік белгісі бойынша классификация тұрғызылады. ( сурет - 2 )
Ұқсас жақындау SHOLKOR - дың басқада платформаларына және параллельді жетектері бар барлық механизмдерге де мүмкін болады.
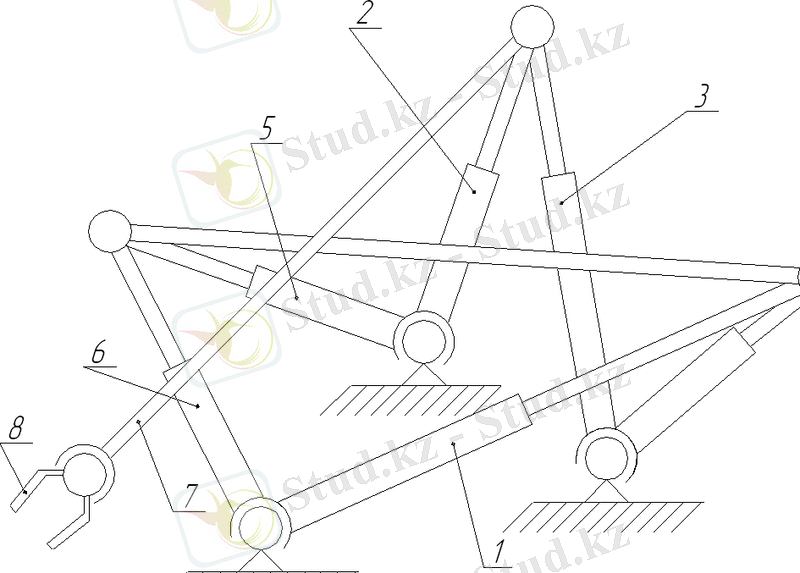
Сурет 1. 2 - Данилевский манипуляторы
1. 2 SHOLKOR платформалық манипуляторын есептеу және жобалау.
Орындаушы робот механизмінде кинематикалық модельдеу үшін 8 параметрлік әдісін қолдану.
Бұл жұмыста 8 параметрлік әдістің негізіне сүйене отырып, параллельді манипулятордың кері және тура есепті шығару үшін қолданамыз. Мысалы: SHOLKOR платформасын аламыз.
Бізге мәлім, орындаушы робот механизмінде шығу буыны (платформа) бірнеше кинематикалық цептің негізімен байланысты. Яғни олардың әрқайсысы жетектерден тұрады. Осындай механизмдерден тұратындарды параллельді структура немесе параллельді манипулятор деп атаймыз. Параллельді манипулятор мысалы SHOLKOR платформасының қаттылығы өте жоғары, әдеттегі манипуляторға қарағанда жүк көтергіштігі осы манипулятордың тура және кері кинематикалық есептелудің аналитикалық шығарылуын ұстап қалады.
Біз SHOLKOR типті платформаға параллельді манипуляторға кинематикалық модельдеуді қолданамыз. Яғни бір типті матрицалық әдіс арқылы 8 параметрлік негізіне сүйене отырып есепті шығарамыз.
Мысалы SHOLKOR платформасы 0 негізінен тұрады, 1 және 2 буыннан 6 кинематикалық цептен тұрады.
Яғни бұл жерде астыңғы цеп 1, 2 буыннан құралған, 1 буын екі қозғалысты сфералық қосылған платформа негізін құрайды, ал екінші жағынан жүргізілген ілгерлемелі жұп бір-бірімен 2 буынмен жалғанған. 2 үстіңгі платформа өз кезегінде үшқозғалысты сфералық жұпты құрайды. Координаттар жүйесін таңдау дененің қозғалысына байланысты болады.
Координаттар жүйесі негізгі және жанама болып екіге бөлінеді. Негізгі координата жүйелері OX0 Y0 Z0 және O X3 Y3 Z3 координаталарымен сәйкесінше 0 негізінен 3 үстіңгі платформамен байланысқан. Сфералық жұптың центрінің басында жанама координата жүйесі ретінде AX1Y1 Z1, BX2 Y2 Z2 таңдалған, яғни олар жоғарғы платформа негізінде сәйкесінше байланысқан. 8 параметрлік әдіспен шығару үшін AX1 Y1 Z1 координата жүйелерін таңдаймыз.
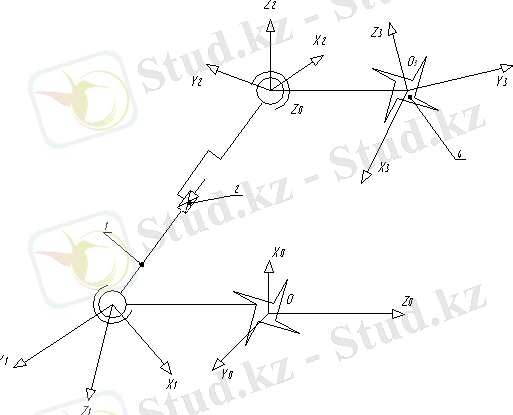
Сурет 1. 3 - Координата жүйесін таңдау сұлбасы
Суретте екі қозғалысты сфералық жұп астыңғы подцепь негізінде көрсетілген. Мұнда, 1 шарлы саусақпен, 2 сфераның үстімен айналады, 3 болатын қиылысу, 4 мұндай қосылу конструкциясы А В осьінің айналасында подцептің айналуын болдырмау үшін таңдалған. A Z1 осьі жанама жүйесі AX1 Y1 Z1 координаталарына қиылысу жалпақтығы арқылы перпендикуляр түрінде бағытталады. AY1 осьі орталық бұрышына биссектриса түрінде басқа қиылысуға қарай бағытталған.
1. 3 Екі қозғалысты сфералық жұп
Кез келген механикалық жүйенің аналитикалық жазылуы, бір типті 8 параметрді қолданып шығарылады. Осы әдістің өзгешілігі, яғни орындалу саны параметрі мен геометриялық параметрлерді толық енгізуіне көмектеседі, олар буын өлшемдерімен байланысты болады. Сонымен қатар кинематикалық жұптардың параметрі түрлендіру параметріне қосылады. Платформа жағдайы үшін математикалық жағдайын қарастырамыз, яғни бір типті матрица көмегімен AX1 Y1 Z1 және BX2 Y2 Z2 жанама координаталар жүйелерінің бірігуіне дейін болады. Сол себепті әрбір қозғалысы бір типті матрицаның элементарлы өлшемдері ( 4 х 4 ) болып жазылады. Ары қарай осы матрицалардың жазылуына келесі шарттар қолданылады.
Мысалы t (z, d) арқылы біртипті матрицаның түрлендірілуі болады, қозғалыс жүйесі O X Y Z осьі бойынша d ұзындықпен жазылады.
Бұл матрицалар былай жазылды:
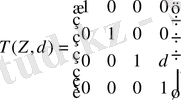
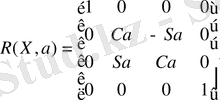 , (1. 1)
, (1. 1)
Әр қозғалысы элементарлы келесі осьтің біріктірілуі толық координата жүйесінің біріктірілуіне бағытталған, яғни олар келесі түрде жазылады:
1. Z1 осьінде жүйенің қозғалуы, d арақашықтығында AX1 Y1 Z1 координата жүйелерінің басын біріктіріп, A нүктесімен қосылып Z1 осьінде A B тура T(z, d) матрицасымен жазылады. Біздің жағдайда d = 0 арнайы таңдалған осьтердің координатасымен болады.
2. Z1 осьінің айналасында Ө бұрышымен бұрылады. Саусақ тәрізді осьімен өтетін осьті біріктіреді. Бұл ауысу R (z1 ө) матрицасымен жазылады.
3. Алынған Y осьінің айналасындағы координата жүйесінің бұрылысы, осьімен бағытталған АВ турасымен сәйкес болғанша алынады. Бұл ауысу R (Y, y) матрицасымен жазылады.
4. X1 осьінің қозғалысының бағыты А координатасы В нүктесімен АВ тура Z осьімен қиылысады, яғни бұрыңғы біріктірілуі болғанға дейін T(x, a) матрицасымен жазылады. Бұл жерде а ауысуы жетектердің жұптары арқылы болады. Сол себептен: А В = L t a, бұл жерде L тұрақты ұзындығы АВ болғанда а = 0 тең болады.
5. X1 осьінің айналасындағы бұрылу d бұрышы Z1 осьіне жалпақ болып орналасады, яғни ол АВ және Z2 осьімен тік өтеді. Бұл орналасу бірінші матрицаның R (x, e) бұрылуымен жазылады.
6. X1 осьімен қатысты бұрылу Ф бұрышына Z осьінің жағдайына байланысты Z1 және Z2 осьтеріне бағытталған. Бұл берілген әрекетке
R (Y, ф) матрицасы жатады.
7. Z2 осьінде B арақашықтығына дейін аралық жүйемен және В2 X2 Y2 Z2 координата жүйесімен ауысады. Бұл ауысулар Т (z, b) матрицасының қозғалуымен жазылады. Міндетті түрде таңдалған арнайы осьтер b = 0 болады.
8. Z2 осьтерінің аймағындағы бұрылыс Z2, ß бұрышына X1 осьімен бағытталып сәйкестендірілуі, ең соңғы жағдайда және X2 осьінде X2 R(x, ß) матрицасымен сәйкестендірілуі соңғы көрсетілген А1 координатасының жүйесі толығымен X1 Y1 Z1 және В2 X2 Y2 Z2 сәйкес болады.
Аналитикалық жазылудың композизиясы келтірілген түрлендіру А12 матрицасын көрсетеді. Біртипті координата жүйесі 0 және 2 денелерімен байланысты. Бұл матрица алынған біртипті матрицаның элементарлы түрлендірудің көбейтіндісінен құрылады:
,
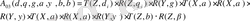 , (1. 2)
, (1. 2)
Егер бұл теңдеуде (1. 2) біртипті матрицаның элементарлы түрлендіргішін қойсақ, онда келесі композицияны аламыз.
 , (1. 3)
, (1. 3)
Бұл жерде бірдей матрицалар қосылмаған T (z, di) және T (z, b) мұнда
i = 1, . . . 6 подцептің ретін анықтайды. Көрсетілген 3 параметр d тәуелсіз ауысу болып келеді. Басқа бұрыштық параметрлер (Ө, γ, d, ф, ß) - сфералық қосылғандағы бұрыштық бұрылуын анықтайды. Бұл жерден тура позиционды кинематикалық есепті, жүйені, қарастырамыз. Яғни ол OX0 Y0 Z және O0 X0 Y0 Z0 координата жүйелерінен ажыратылады. Матрица түрлендіргішінің OX0 Y0 Z0 жүйесіне ауысу кезінде AX1 Y1 Z1 жанама координат жүйесін Т' (0 0) - ны белгілейміз, ал матрицаны түрлендіргішке ауыстыру Т' (0 0) және Т' (3 3) бізге мәлім бұрыштық тұрақты және сызықты ұзындық болады, яғни манипулятордың конструкциялық өлшемдерінен тұрады.
Сол себепті платформаның қозғалу жағдайы сәйкесінше базалық координата жүйесінде Т3 матрицасы арқылы анықталады.
Сондықтан Т3 матрицасы мынадай структурада болады:
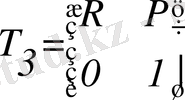 , (1. 4)
, (1. 4)
бұл жерде R - матрицасы ( 3 х 3 ) O3 X3 Y3 Z3 осьінде беріледі,
р - векторы ( 3 х 1 ), OX0 Y0 Z0 координата жүйесінде, О3 координата нүктелерінен құралған, яғни OX0 Y0 Z0 координата жүйесінде құралады.
Алынған теңдеуден, қозғалу платформасының жағдайы базалық жүйенің координата жүйесімен анықталады, нәтиже бойынша келесі матрицалық теңдеу жазылады:
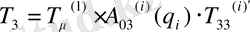 , (1. 5)
, (1. 5)
Мұнда, q1 = q1 жалпыланған манипулятордың координатасы
6 матрицалық теңдеудің түрі тәуелді және теңдеу жүйесі арқылы шығарылады. Тура позиционды кинематикалық есепті шығару кезінде, жалпыланған координата беріледі. Бірінші этапта, Т3 ескермегенде,
(өi, yi, di, fi, ßi) анықтауымыз керек.
Сосын (1. 5) теңдеуін қолдана отырып диагональды элементтерін түзете отырып 6 алгебралық теңдеуді аламыз, яғни олардан белгісіз ұзындықтарды анықтаймыз. Базалық координата жүйесінде платформаны сипаттаймыз. Аналитикалық тәуелділіктің көмегімен (1. 5) позиционды тура және кері есепті шешуге болады.
Енді кері позиционды кинематикалық есепті қарастырамыз. Кері матрицаға қөбейтуді қолданамыз. (1. 5) тең түрге келті
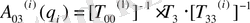 , (1. 6)
, (1. 6)
А' 03 (q i) матрицасының орнына қоямыз, одан шыққан теңдеуді
кері матрицаға көбейтуді қолдана отырып, мынаны аламыз:
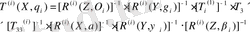 , (1. 7)
, (1. 7)
(1. 7) теңдеуі 6 матрицалық теңдеуден тұратын жүйені құрайды, яғни
онда 36 ұзындық болады. Бұл 30 бұрыш (өi y idi fi ßi) және 6 жалпыланған.
Орналасқан жағдайы және платформа орентациясы болады, яғни Т3
матрица элементтерін түзетеді, мысалы, диагональді элементтің
теңдеуінен 71, 36 теңдеуді аламыз, олардан іздеген ұзындықтарды
анықтаймыз.
Математикалық жазылудың механикалық жүйеде есеп шығуы 2
этапқа бөлінеді. Бірінші этапта біз қажет матрицалық түрлендіргішті
анықтаймыз, және аналитикалық жазылу жүйесін сипаттаймыз. Екінші
этапта алгебралық теңдеуде жүйенің шығуы қарастырылады, және
қарастырылып отырған ұзындықтар анықталады. Есепті шығару
эффектісі екінші этапта алгоритм мүмкіншілігі және есептеуіш техника түрінде анықталады. Бұл жерден есепті программалау деңгейі және компьютерлік техникада дәл қазіргі кезде кез келген қиындықтардағы математикалық модельді шығаруға болатындығын ескере кету қажет. Осы есептер дәлдікпен байланысқан және жылдамдық есептеулеріне байланысты, мамандардың қатысуларымен әр кезде шығарылып келеді.
Сол себептен бірінші пландағы проблема адекватты математикалық модельдеуді шешу болып табылады, мысалы математикалық модельдеудің жалғасы ретінде параллельді манипулятор типті SHOLKOR платформасын алуға болады. 8 параметрлі түрлендіргіш әдісімен жалпыланған ауыспалы манипулятор координатасын бөліп аламыз. Бұл бізге кинематикалық модельдеуді құруға көмектеседі жәнеде кері және тура позиционды кинематикалық есепті шығаруға болады.
Алынған матрицалық теңдеу паралелльді манипулятор типті SHOLKOR платформасы үшін тура және кері кинематика есебін шығару кезіндегі алгоритмі көрсетілген.
1. 4 Буындардың координата жүйесіндегі
кинематикалық параметрі
Кинематикалық параметрдің локальді координатасына қатынасы, координатасына қатынасы, координата жүйесінде буындардың байланысын есептеу, i - буынымен негізделіп есептеледі, сол себепті матрицаның бір бөлігі кинематикалық жұпта қолданылады, түрлендіру буындарының жүйесінің бір-біріне деген қатынасын жазамыз:
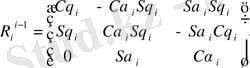 , (1. 8)
, (1. 8)
Бұл жерде матрица Ri ортонормаланған болып келеді, сол себепті өз кезегінде былай жазылады:
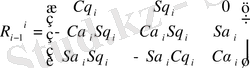 , (1. 9)
, (1. 9)
R' i-1 матрицасы i - 1 координат жүйесінен i жүйесіне дейін өлшемді векторды түрлендіреді.
(1. 7) берілген кинематикалық параметрлерінде i - 1 координат жүйесінде жазылады. R'i -1 матрица көмегімен кинематикалық жұп локальді i - координата жүйесінде жазылуы мүмкін. Бұл жағдайда (1. 7) формулалары ілгерлемелі кинематикалық жұбында келесідей болып түрленеді:
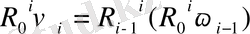
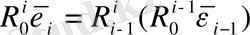
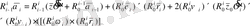 , (1. 10)
, (1. 10)
Егер бір - бірімен тығыз байланысқан буын айналмалы кинематикалық жұпты құраса, онда жылдамдатылған локальді координат жүйесі жылдамдық үшін мынадай түрде болады:
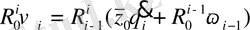
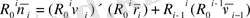
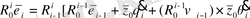
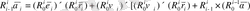 , (1. 11)
, (1. 11)
Нәтиже бойынша, алынған векторлық теңдік, локальді координат жүйесінде әртүрлі кинематикалық параметрді анықтайды, буындармен келесі жағдайда байланысты болады, яғни бір бірімен байланысқан буындар қозғалысына байланысты айналмалы және ілгерлемелі қозғалыс жасайды.
1. 5 Параллельді манипулятордың күш анализі
Параллельді манипулятордың күш анализін есептеу үшін рекурентті тәуелділігін енгіземіз, динамикалық анализ үшін Ньютон - Эйлер әдісін қолданып отырамыз.
Есептелген (сурет 1. 3) сұлбасында көрсетілгендей, О і-1, Оі,, нүктесінің орналасуы, яғни координат жүйесінің басы болады, і - 1, і, буындарымен сәйкесінше байланысады, қозғалмайтын координат жүйесінле р¯і-1, р¯і
радиус - векторымен анықталады. Psi радиус - векторы
Si - массаның центрі і буынының базалық жүйе есеп беруінде анықталады. Ri Oi Si Oi Si векторы сәйкесінше і координа жүйесінің қатынасы і - 1-ге орналасуын суреттейді, сол себепті Si масса центрінің орналасуы і-1 және і координата жүйесіне қатысты болады. О і-1 күш реакциясы Fi қозғалуы і-1 буыннан і-буынға дейін болады. Мі басты векторы арқылы өтетін і буын моментімен і-1 буынының күш реакциясынан тұрады. К нүктесінде күш болады, рі жетегімен іске асырылады. Бұл жерде келесі жағдай қарастырылады, жұмыстарда [ ] беріледі, бұл күштер і- буынына қатысты болады, бұл жетектерден үдеу бөлектенген. Бұл көбінесе манипулятор жетегінің құрылуына байланысты болады. Осы жағдайда, жұптасу қозғалысы айналу жетегінің құрылуына байланысты болады.
Яғни бұл момент жетекпен бегіленеді. Шарнирді Мі реакциясында момент күшінің құрылуы қарастырылады. І буыны дене жүйесі болып қарастырылады, Si центр массасының жүйесіне ауырлық Gi күшінің суммарлы қойылу керек ( бүкіл жетекті ) қосқанда. і + 1 буынына і буыны жағынан суммарлы күш іске қосылады. Сол кезде Ньютонның
3-ші заңы бойынша, і буыны жағынан і + 1 буынына күш әсер етеді, яғни ол ( Fi + 1 ) және момент ( -Mi + 1 ) -ге тең болады.
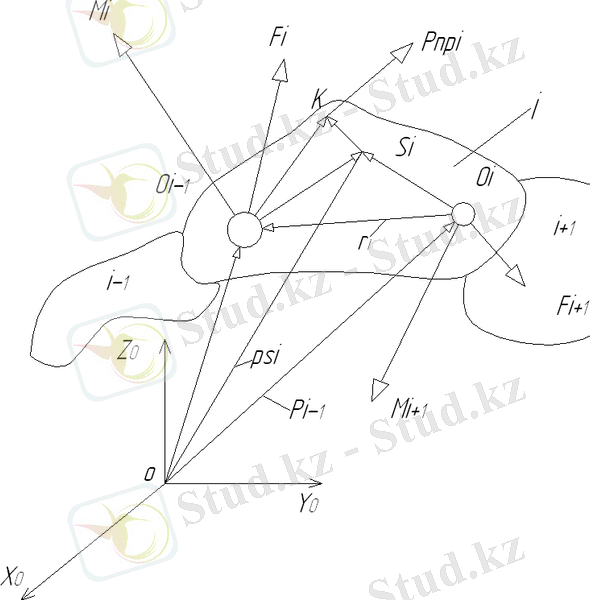
Сурет 1. 4 - Күш анализін есептелу сұлбасы
Қозғалыс центрінің массасы і- буынына байланысты теоремасына сәйкес:
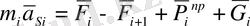 , (1. 12)
, (1. 12)
Бұл жерде mi asi - сәйкесінше масса және і массасының буыны жағдайымен болады.
Кинетикалық моменттің қатысының теорема бойынша өзгеруі О қозғалыс бойынша, і буыны үшін жазылады, сонда вектор теңсіздігі келесідей болады:
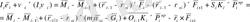 , (1. 13)
, (1. 13)
(1. 13) тензор итерация нүктесінің і денесінде болады. Нүкте орналасуының жетекпен рі қатысты центр массасы арқылы Оі-1 Кі теңсіздік векторын анықтаймыз:
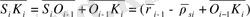 , (1. 14)
, (1. 14)
Бұл жерден жетек үдеуінің кинематиклық жұптары ( Si Ki = Ө ),
Pi,, Oi-1, Z i-1 осьі бойынша реакция күшіне қосылады.
( 1. 14 ) рекурентті форма түрінде болуы мүмкін:
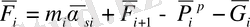
 , (1. 15)
, (1. 15)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz