Графтардағы Гамильтон циклдері мен жолдары және классикалық жүйелердің фазалық сипаттамалары


МАЗМҰНЫ
Кіріспе
Дискретті математика негіздері Егер үлкен есептеу жүйелері құрылса, онда олардың қандай да бір пайда болған үлкен есептерді шешу үшін қажеттілігі болғаны. Кез-келген салада әр түрлі мәселелер, яғни соған байланысты жүздеген, мыңдаған сұрақтар пайда болуда. Ал олардың жауабын іздеудің жалпы қағидалары өте ертеректе құрастырылған. Бірінші, осы объектінің немесе процестің математикалық моделін құрудан бастайды. Математикалық модельдеу объектінің белгілі бір болмысын немесе болып жатқан процестерді теңдеулер тілінде және басқадай математикалық құралдар арқылы көрсету. Яғни, математикалық модель зерттеу облысына қатысты қандай да бір дифференциалдық, интегралдық алгебралық немесе басқа да бір өрнектер жиыны. Осы алынған математикалық модельді, яғни теңдеудінемесе әртүрлі теңдеулер жүйесін шеше отырып, біз қойылған сұрақтардың жауабын ала аламыз. Әрине, компьютерлер қаншалықты қуатты болғанымен олар өз беттерінше берілген есептерді шеше алмайды. Олар тек қана өте қарапайым амалдарды ғана орындай алады. Ал олардың бүкіл интеллектуалдық күші адам құрастырған бағдарламалармен анықталады. Бағдарламалар қандай да бір мақсатқа құрылған қарапайым амалдар тізбегін іске асырады. Шешімді іздеу, қарапайым амалдар тізбегін орындау процесіне келіп тіреледі. Бұл алгоритмді құрастыру деп аталады. Дискретті математика және математикалық логика пәні математика білімінің бөлінбес бір бөлігі болып саналады.
Дискреттік Математика- математиканың дискретті құрылымдардың қасиеттерін зерттейтін саласы. Мұндай құрылымдарға шектеулі топтар, шектеулі графтар, сондай-ақ, ақпаратты түрлендіргіш кейбір математикалық модельдер, шектеулі автоматтар, Тьюринг машинасы, және т. б. жатады. Компьютерлерді жасау және пайдалану программалау тілдері, ақпаратты өңдеу және тарату жабдықтары, автоматтандырылған басқару және жобалау жүйелері мамандарының зерттеу жұмыстары үшін дискретті математика әдістері негізгі құрал, ал дискретті математика тілі осы мәселелер бойынша пайдаланатын ғылыми және техникалық тіл болып табылады. - программалау процесінде жасанды интеллект есептерін шығаруда, программалардың дұрыстығын дәлелдеуде модельдеуді пайдалануға дағдыландыру. Компьютерлік ғылымның теориялық фундаменті болып саналатын дискретті математика арқылы сипаттағы құрылымдар қасиеттерін зерттейтін математиканың бір саласы болып саналады.
1 Графтардағы Гамильтон циклы мен жолы
Гамильтон циклі (жолы) дегеніміз графтың барлық қабырғаларын қамтитын қарапайым циклді(жолды) айтамыз. Гамильтон циклінің сыртқы анықтамасы Эйлер циклінікіне ұқсас. Алайда, ең басты айырмашылық сәйкес тапсырмалардың сипатталуы мен құрылуы кезінде шешу қиындығында. Біз Эйлер циклінде жетерліктей қарапайым болу өлшемі жәнеде оны шешудің тиімді құрылымдық алгоритімі бар екенін көрдік. Гамильтон циклі үшін бір де бір жай ғана тексерілетін қажетті және жеткілікті болу шарттар белгісіз, ал белгілі алгоритімдер қайсы бір графтарға үлкен сандық варианттарды қоюды талап етеді.
Гамильтон циклі комбинаторикалық көзқарас бойынша граф төбелерінің орын ауыстыру болып табылады. Сондай-ақ циклдің бастапқы төбесі ретінде кез келген төбені алуға болады, сондықтан орынауыстыруды белгіленген алғашқы элементтен бастай беруге болады. Гамильтон циклін табу жоспарының ең қулықсыз жолы, ол барлық орынауыстыруларды ретті түрде қарастырып шығу және оның әрқайсысына тексеру жүргізу болып табылады, және де ол берілген графта циклді көрсете ала ма.
Осындай әдіс төбелер санының аз мәнінде, орынауыстыру санының тез өсу салдырынан тіпті орындалмайтындай болады, белгілеп алынған бірінші элементпен бірге элементтен орынауыстыру.
1. 1 Графтардағы ені бойынша іздеу процедурасы
Кез келген алгоритмдердің қарастырылуы немесе есептелуі үшін графтардың қабырғаларының кезектесіп орналасуна байлынысты қарастырылады. Жалпы, графтарды қарастыру үшін қандай іс атқарылатындығы қарастырылу (обход) үшін тапсырманың нақтылығына қатысты болады. Барлық жағдайда төбелердің қарастырылуы есептің басынан аяғына дейін қатысып, қатысушы ретінде сақталып отырады. Қатыстырылмаған төбені немесе қабырғаны жаңа төбе деп атаймыз. Ал төбелер қатысып, қарастырылуымен ұзындыңтар ашық түрде болады, соған байланысқан барлық төбелер қарастырылып болмайынша ол жабық түрде бола алмайды. Тек содан кейін ғана ол жабық түрге айналады.
Ені бойынша іздеу идеясы - бірнеше алдын ала таңдалған қабырғалардың немесе бастапқы көрсетуші қабырғасының өшірілу ретімен қатыстырудан тұрады. Басқаша айтқанда, алдымен қабырғасы өзі қатысып, сосын осы қабырғасымен қатысты 1 аралықта табылған, содан кейін одан 2 аралықта табылған төбелердің қатысуы болып табылады.
Бастапқы берілген төбесінің ені бойынша іздеуді қарастырайық. Басынды барлық қабырғалар жаңа түрінде орналастырылады. Бірінші төбесі қатыстырылып, тек осы ұзындық қана ашық қабырға бола бастайды. Ары қарай әр кезекті қадам бірнеше ашық төбені таңдаумен қарастырылу басталады. Осы қабырға белсенді бола бастайды. Содан кейін қабырға, белсенді инцидиентті төбе зерттеле бастайды. Егер осындай төбе сияқты жаңа ұзындығын біріктірсе онда қабырғасы ашық түрге айналады. Барлық қабырға белсенді инцидиетті ұзындықта болған кезде ашық түрден жабық түрге айналуы зерттеледі. Осыдан кейін жаңа белсенді ұзындық таңдалады және іс-әрекет қайталанады. Ашық ұзындықтар жиыны бос жиынға тең болғанда процесс аяқталады.
Графтарды қарастырудың басқа әдістерінен ені бойынша іздеудің басты ерекшелігі белсенді төбенің қасиеті: бұрын байланысқан ашық жиыннан таңдалуымен ерекшелінеді. Ені бойынша іздеудің ерекшелігі қаншалықты жақын орналасса соншалықты оқиға ерте орындалады. Осы қағиданың жүзеге асуы үшін жаңа жиыннан шыққан төбелер ашық жиындарға келіп кезекке қою қойылады, жаңа жиын ашық жиынға айналған кезде соңғы кезекке қосылады, ал белсенді кезектін басынан таңдалады.
1. 2 Графтардағы маршруттар, жолдар, циклдар
Графтағы маршрут - және, тобелері үшін, қабырғалармен байланысқан төбелерінің тізбегі. Мұндағы қабырғалар маршрут қабырғалары деп аталады. Маршрутты солардан өтетін деп айтамыз да, сол саны маршрут ұзындығы болады. Және де маршрут және төбелерін қосадыдейміз де, олар сәйкесінше маршруттың басы және аяғы болады, ал олардың арасындағы төбелері аралық төбелер болады. Егер де болса, маршрут тұйық болады.
Жол - барлық қабырғалары әр түрлі маршрут. Егер де жолдың барлық төбелері де әр түрлі болса, ол жол қарапайым деп аталады.
Цикл - бұл тұйықталған жол. Егер де төбелері қос-қостап әр түрлі болса, циклы қарапайым болады.
1 теорема. Әр түрлі төбелерді қосатын кез-келген маршруттың құрамында сол төбелерді қосатын қарапайым жол болады. Кей қабырғадан өтетін кез-келген циклде сол қабырғадан өтетін қарапайым цикл болады.
Дәлелдеу. маршруты бар болсын. Егер де оның барлық төбелері әр түрлі болса - бұл қарапайым жол. Егер олай болмаса, , болсын. Ондайда осы маршруттан мен, аралығын жою арқылы алынған тізбегі де маршрут болып табылады. Жаңа маршрут сол төбелерді қосады, және қысқалау болады. Ары қарай да осылай істеу арқылы, белгілі бір «түзеулер» санынан соң және төбелерін қосатын қарапайым жолды аламыз. Теореманың 2-ші сөйлемі де осылай дәлелденеді.
Және де 1 теоремадағы «цикл» сөзін «тұйық маршрут» сөзімен ауыстыруға болмайтынын айта кету керек.
2 теорема. Егер де графтың әрбір төбесінің дәрежесі 2 ден кем болмаса, онда цикл бар.
Дәлелдеу. Графта ең ұзын қарапайым жолды табайық. Ол болсын. төбесі -мен көршілес, және де оның дәрежесі 2-ден кем емес болғандықтан ол кемінде тағы да бір төбемен көршілес, ол төбе мысал үшін болсын. Егер де жолдың басқа төбелерінен бөлек болса, ондатізбегі ұзындау қарапайым жол болар еді. Сондықтан - жолдың төбелерінің бірі, мұнда . Бірақ ондайда цикл болып табылады.
Графтің әр бір төбесі бір рет кіретін циклді гамильтон циклі деп аталады, ал осындай циклі бар графті гамильтон графы деп аталады.
Гамильтон графтар түсінігі ирландиядан В. Гамильтон ирландияның математигімен байланысты, ол 1859 жылы, додекаэдр графында гамильтон циклі табылатындай, «кругосветное путешествие» ойынын шығарды.
3 теорема.
Егер
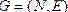 байланыс графтің ең ұзын
байланыс графтің ең ұзын
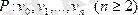 жай тізбесі және
жай тізбесі және
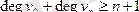 болса
,
онда
болса
,
онда
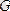 графі гамильтон болып табылады.
графі гамильтон болып табылады.
Гамильтон циклдары туралы есептің интерпритациясы ретінде ең көп тараған коммивояжер туралы есепті қарастыруға болады. Коммивояжер аралайтын бірнеше қалалардың арақашықтықтары белгілі. Барлық қалаларда бір реттен ғана болып алғашқы шыққан қаласына қайтып келетін маршрутты табу керек. Егер мұндай маршруттар бірнешеу болса, олардың ең қысқасын табу керек. Мұндай есептер іс жүзінде жиі кездеседі, мысал үшін өндіріс өнімдерін сауда орталықтарына ең қысқа жолмен жеткізу есебі. Мұндай есептерді шешудің жалпы ортақ теоремалары мен көлемі жөнінен шағын, әрі тиімді алгоритмдердің жоқтығы есепті шешуде қиындықтар туғызады.
Анықтама. Айталық G(V, E) байланысты бағытталмаған граф. G графының барлық төбелері арқылы өтетін, басталуы мен аяқталуы әр түрлі төбелерде болатын қарапайым цикл Гамильтон циклы деп аталады. Графтарда Гамильтон циклдары мен шынжырлары бар болудың 87 жеткілікті шартын келтірейік. Айталық дәр. v - vÎV төбесінің дәрежесі болсын. Теорема. Егер G (V, E), мұндағы V =n графында кез келген төбелер vi vj жұбы үшін дәр. vi + дәр. vj ≥n-1, орындалса, графта гамильтон шынжыры бар, ал егер дәр. vi + дәр. vj ≥n немесе дәр. vi ≥n /2 графта Гамильтон циклы бар.
2 Классикалық жүйенің фазалық сипаттамалары
Макроскопиялық жүйенің динамикалық сипаттамалары. Макроскопиялық жүйелерді зерттеу үшін модель керек. Яғни оның кіші элементтері көрсетіліп, олардың өзара әсерлесуі қандай болатындығын көрсету керек. Қозғалысын классикалық немесе кванттық әдіспен сипаттай ма? Микробөлшектердің қозғалысын сипатттау үшін кванттық әдісті қолданады, бірақ ілгерілмелі қозғалысты классикалық әдіспен сипаттауға болады. Әрбір бөлшектің орны-
 (х, y, z. ), импульстары
(х, y, z. ), импульстары
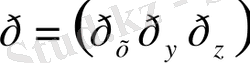 шамалармен сипатталады. N бөлшектің қозғалысын сипаттау үшін 6N өлшем саны керек: оның 3N-і координаттар және 3N-і импульс құраушылары. Егер бұл шамалар бір-бірінен тәуелсіз болса, бұл шамалар саны (6N) еркіндік дәрежелерінің санына тең. Осы шамалар берілсе, жүйенің микроскопиялық күйі берілді деп есептеледі. Уақыт өткен сайын бұл шамалар өзгереді, яғни жүйенің микрокүйі өзгереді. Бұл қозғалыс
Гамильтон теңдеулерімен
сиптталады.
шамалармен сипатталады. N бөлшектің қозғалысын сипаттау үшін 6N өлшем саны керек: оның 3N-і координаттар және 3N-і импульс құраушылары. Егер бұл шамалар бір-бірінен тәуелсіз болса, бұл шамалар саны (6N) еркіндік дәрежелерінің санына тең. Осы шамалар берілсе, жүйенің микроскопиялық күйі берілді деп есептеледі. Уақыт өткен сайын бұл шамалар өзгереді, яғни жүйенің микрокүйі өзгереді. Бұл қозғалыс
Гамильтон теңдеулерімен
сиптталады.
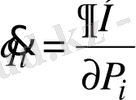
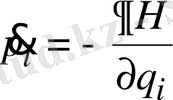 і
=1, 2, . . . 3N (1. 1)
і
=1, 2, . . . 3N (1. 1)
Осы теңдеулерді шешіп, жүйенің микроскопиялық күйін табуға болады. Микрокүйлердің энергиялары бойынша ортақ тобы- бір макроскопиялық күйге сәйкес келеді. Гамильтон функциясы еркін бөлшек үшін энергия болып табылады.
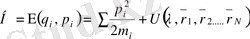 (1. 2)
(1. 2)
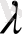 -жүйеге сыртқы әсер параметрлері. Бөлшектердің өзара әсері әлсіз болса, жуықтап нөлге тең деп қабылдауға болады. Онда тек сыртқы әсер қалады. Бұндай жүйе- идеал газ деп аталады.
-жүйеге сыртқы әсер параметрлері. Бөлшектердің өзара әсері әлсіз болса, жуықтап нөлге тең деп қабылдауға болады. Онда тек сыртқы әсер қалады. Бұндай жүйе- идеал газ деп аталады.
Сонымен, N - бөлшектен құрылған жүйені сипаттау үшін 6N шама қажет болады. Осы шамалардың кейбіреулері бір-біріне тәуелді болса, онда еркіндік дәрежелерінің саны 6N -нен кем болады. Классикалық механиканы өткен кезде, механикалық қозғалыстарды зерттеуді жеңілдету мақсатында шартты кеңістік түрлері енгізілді. Тек координаттардан құралған кеңістік- геометриялық кеңістік деп аталады. Барлық координаттар мен уақыттан құралған шартты кеңістік- конфигурациялық кеңістік деп аталады. Ал координаттардан және импульс құраушыларынан құралған шартты кеңістік- фазалық кеңістік деп аталады. Жүйенің өзгерістерін сипаттау үшін 6N өлшемді шартты кеңістік енгізіп, сондағы шартты нүктенің қозғалысы түрінде бұл өзгерістерді қарастыруға болады. Фазалық кеңістік деп осындай кеңістікті атайды. Бұл кеңістіктің әрбір нүктесінің 6N координаты бар. Әрбір нүкте жүйенің белгілі- бір микроскопиялық күйін анықтайды. Бұл нүкте жүйенің бейнелеуіш нүктесі деп аталады. Ал жүйені сипаттайтын шамалардың кейбіреулерінің бір-бірімен байланысын сипаттайтын теңдеулер фазалық кеңістікте сызықты анықтайды. Бейнелеуіш нүктенің фазалық кеңістікте уақыт өткен сайын орын ауыстыратын жолы фазалық траектория деп аталады. Оның теңдеулері:
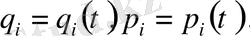 i
=1, 2, 3, . . . 3N (1. 3)
i
=1, 2, 3, . . . 3N (1. 3)
Бұл теңдеулер Гамильтон теңдеуінің шешімдері болып табылады. Фазалық кеңістіктің көлем элементі
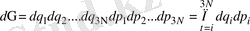 (1. 4)
(1. 4)
қысқаша белгісі:
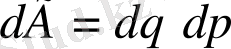 . Декарттық координат жүйесінде
. Декарттық координат жүйесінде
dГ=
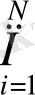 (dxdydzdp
х
dp
у
dp
z
)
і,
немесе dГ=d
r
d
p
(1. 5)
(dxdydzdp
х
dp
у
dp
z
)
і,
немесе dГ=d
r
d
p
(1. 5)
Сонымен фазалық кеңістік элементі екі кеңістіктің элементтерінің көбейтіндісі болып табылады: dp- импульстар кеңістігі элементі, dq- конфигурациялар кеңістігі элементі. Яғни жалпы айтқанда:
Фазалық кеңістік= импульстар кеңістігі + конфигурациялар кеңістігі.
Фазалық кеңістікті әрбір бөлшектің кеңістікшесі 6 өлшемді болатындай етіп бөлсе, онда фазалық кеңістік N кеңістікшеден құрылады, әрқайсысы 6 өлшемді. Ғылыми әдебиетте бір бөлшектің 6-өлшемді кеңістігін μ-кеңістік деп атайды, ал N бөлшектің 6N-өлшемді кеңістігін Γ-кеңістік деп атайды. Изоляцияланған жүйенің микрокүйлері (бейнелеуіш нүктелері) фазалық кеңістіктің шектелген аумағында орналасқан.
Мысал 1 : Бір бөлшектің фазалық μ- кеңістік көлемін табу керек.
Бір бөлшектің үлесіне тиетін фазалық μ- кеңістік көлемі:
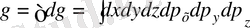 . (1. 6)
. (1. 6)
Осы интегралды табайық. х, у, z координатасының өзгеру шегі - ыдыстың көлемімен шектелген. Бөлшектің кеңістіктегі орны оның импульсына тәуелді емес. Сондықтан
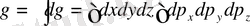 (1. 7)
(1. 7)
интегралдаулар бір бірінен тәуелсіз орындалады.
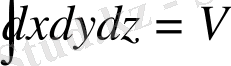 - ыдыс көлемі. Энергия мен импульстың классикалық физикадағы өзара байланысы:
- ыдыс көлемі. Энергия мен импульстың классикалық физикадағы өзара байланысы:
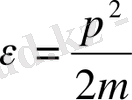 Бірақ бөлшек энергиялары шектеулі болғандықтан (
Бірақ бөлшек энергиялары шектеулі болғандықтан (
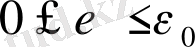 ), импульстары да шектеулі болуы тиіс:
), импульстары да шектеулі болуы тиіс:
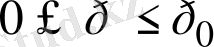 . Мұнда бөлшек импульсының ең үлкен мәні:
. Мұнда бөлшек импульсының ең үлкен мәні:
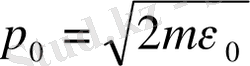 . Импульс векторлы шама болғандықтан, қозғалыс бағыттары алуан түрлі болуы мүмкін
. Импульс векторлы шама болғандықтан, қозғалыс бағыттары алуан түрлі болуы мүмкін
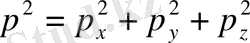 , әрбір жеке декарттық құраушысы үшін табатынымыз:
, әрбір жеке декарттық құраушысы үшін табатынымыз:
р z
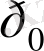
O р y
р x
1-сурет. Импульстардың шартты кеңістігі.
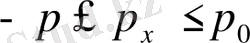 ;
;
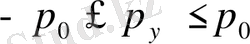 ;
;
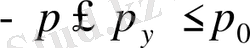 ;
;
сондықтан бөлшектің мүмкін микрокүйлері импульстар кеңістігінде радиусы
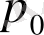 сферасының ішкі аумағын толтыратындығы көрінеді. Радиусы p
0
- шардың көлемі
сферасының ішкі аумағын толтыратындығы көрінеді. Радиусы p
0
- шардың көлемі
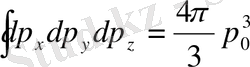 (1. 8)
(1. 8)
Сондықтан микрокүйлерге сәйкес импульс кеңістігінде алатын көлемі
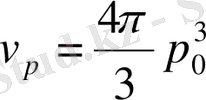 . Сонымен, қорытындылай келгенде бір бөлшектің фазалық кеңістіктегі қозғалатын аумағының көлемі:
. Сонымен, қорытындылай келгенде бір бөлшектің фазалық кеңістіктегі қозғалатын аумағының көлемі:
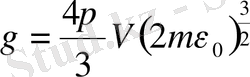 . Ал энергиясы
. Ал энергиясы
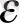 -нан
-нан
 -ге дейін бөлшек микрокүйлерінің барлығына қандай элементар фазалық көлем сәйкес келеді? -деген сұраққа:
-ге дейін бөлшек микрокүйлерінің барлығына қандай элементар фазалық көлем сәйкес келеді? -деген сұраққа:
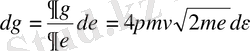 - (1. 9)
- (1. 9)
деп көрсетуге болады.
Мысал 2 : Көлемі V ыдыстың ішінде бірдей N бөлшек болсын. Осы физикалық жүйенің фазалық көлемін табайық. Энергияларының қосындысы 0÷Е аралығында болсын. Молекулалардың өзара әсерлесуі олардың энергияларын өзгертеді, бірақ бір бөлшектің энергиясы 0÷Е шегінен шықпайды.
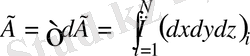
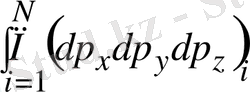 (1. 10)
(1. 10)
барлық бөлшектер координаталары V көлемнің ішінде, сондықтан
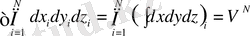 (1. 11)
(1. 11)
Фазалық көлем:
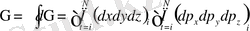
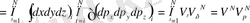 (1. 12)
(1. 12)
Жүйенің толық энергиясы жүйе бөлшектерінің энергияларының қосындысына тең.
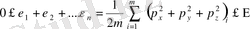 Ал импульстар кеңістігінде импульс проекцияларының өзгерістері өзара тәуелсіз емес, өзгеру шектері
Ал импульстар кеңістігінде импульс проекцияларының өзгерістері өзара тәуелсіз емес, өзгеру шектері
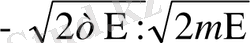 аралығында, яғни
аралығында, яғни
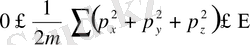 . Олардың әрқайсысы
. Олардың әрқайсысы
 -ге дейінгі мәндердің кез келгеніне ие болуы мүмкін. Импульстар кеңістігінде бұл теңсіздік радиусы-
-ге дейінгі мәндердің кез келгеніне ие болуы мүмкін. Импульстар кеңістігінде бұл теңсіздік радиусы-
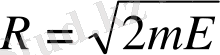 гиперсфераны бөліп шығарады. Оның центрі координаттық жүйесінің төбесінде орналасады. Импульс кеңістігіндегі интегралдың мәні осы гиперсфераның көлеміне тең. Импульстық кеңістіктегі өлшемдер саны 3N, екі өлшемді жазық бетте дөңгелектің ауданы R
2
-қа пропорционал болады десек, үш өлшемді кеңістікте сфера көлемі R
3
-ке пропорционал болар еді:
гиперсфераны бөліп шығарады. Оның центрі координаттық жүйесінің төбесінде орналасады. Импульс кеңістігіндегі интегралдың мәні осы гиперсфераның көлеміне тең. Импульстық кеңістіктегі өлшемдер саны 3N, екі өлшемді жазық бетте дөңгелектің ауданы R
2
-қа пропорционал болады десек, үш өлшемді кеңістікте сфера көлемі R
3
-ке пропорционал болар еді:
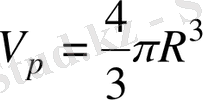 Ал 3N өлшемді кеңістікте гиперсфера көлемі
Ал 3N өлшемді кеңістікте гиперсфера көлемі
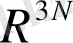 -ге пропорционал деп айтуға болады. Сонымен,
-ге пропорционал деп айтуға болады. Сонымен,
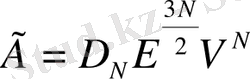 (1. 13)
(1. 13)
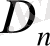 тұрақты көбейткіш. Осыдан dE энергия интервалына сәйкес келетін фазалық көлем элементі:
тұрақты көбейткіш. Осыдан dE энергия интервалына сәйкес келетін фазалық көлем элементі:
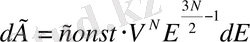 (1. 14)
(1. 14)
Сонымен классикалық макрожүйені сипаттау үшін 2f өлшемді фазалық кеңістік қажет: f- жалпылама координат саны және f-жалпылама импульс кеңістігінің өлшемі. Бұл кеңістікте бейнелеуіш нүкте жүйенің микроскопиялық күйіне сәйкес келеді. Консервативті жүйелер үшін
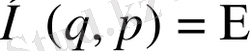 (тұрақты) Сондықтан фазалық траектория тұрақты энергияға сәйкес келетін белгілі бір гипербетте жатады.
(тұрақты) Сондықтан фазалық траектория тұрақты энергияға сәйкес келетін белгілі бір гипербетте жатады.
2. 1 Экстремальдық әсер принципі (Остроградский - Гамильтон принципі)
Енді Лагранж тендеулері механиканың кейбір вариациялық есептері үшін Эйлер теңдеуі болатындығын көрсетейік. Ол үшін механикалық жүйенің конфиурациялық кеңістігі деген ұғым енгізейік.
Механикалық жүйенің конфигурациялық кеңістігі деп, q1, q2, …, qs, жалпыланған координаттарға және t уақытқа тәуелді (s+1) өлшемді кеңістікті айтады.
Егер абсцисса өсінің бойына t уақытты ал ордината өсінің бойына qα жалпыланған координаттар жиынын салсақ, онда осы жазықтықта жатқан (qα, t) координаттары мен анықталатын нүкте t уақыт мезгіліндегі жүйенің белгілі бір конфигурациясына сәйкес келеді.
Механикалық жүйе (t2-t1) уақыт ішінде А конфигурациясынан В конфигурациясына орын ауыстырды дейік (1-суретті қара) және жүйеге түсірілген байланыстар оның ықтималдық орын ауыстыруын шектемейтін болсын, басқаша айтқанда, жүйе А конфигурациясынан В конфигурациясына ықтималдық орын ауыстыруды бірнеше траекториялармен өте алатын болсын, ал солардын ішінде біреуі ғана (АСВ) жүйенің шын орын ауыстыруына сәйкес келсін.
Осы шын орын ауыстыру траекториясын, мүмкін болатын бірнеше ықтималдық орын ауыстырулардың ішінен қалай бөліп алуға болады, деген сұраққа экстремалдық әсер принцпі (Остроградский- Гамильтон принципі) жауап береді. Идеалдық байланыста және потенциалдық (немесе жалпыланған потенциалдық) белсенді күштер өрісінде тұрған голономдық механикалық жүйелер үшін бұл принципті былай тұжырымдауға болады;
Механикалық жүйенің А конфигурациясынан В конфигурациясына, мүмкін болатын бірнеше ықтималдық орын ауыстыруларының ішінен, шын орын ауыстыру әсер функциясының экстремалдық (көп жағдайда ең аз) мәніне сәйкес келеді.
Басқаша айтқанда механикалық жүйенің шын орын ауыстыру траекториясында (1) -әсер функциясының бірінші вариациясы нольге тең болуы керек, яғни
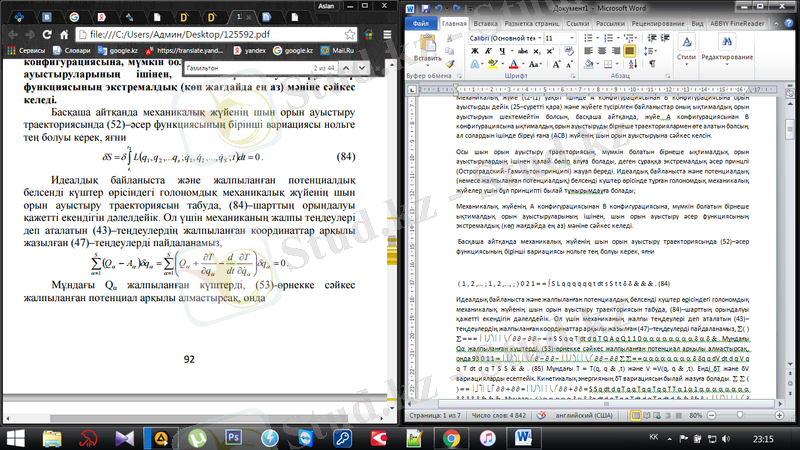 (2. 1)
(2. 1)
Идеалдық байланыста және жалпыланған потенциалдық белсенді күштер өрісіндегі голономдық механикалық жүйенің шын орын ауыстыру траекториясын табуда, шарттың орындалуы қажетті екендігін дәлелдейік. Ол үшін механиканың жалпы теңдеулері деп аталатын (2) -теңдеулердің жалпыланған координаттар арқылы жазылған (2) -теңдеулерді пайдаланамыз,
 (2. 2)
(2. 2)
Мұндағы Q α жалпыланған күштерді, (2) -өрнекке сәйкес жалпыланған потенциал арқылы алмастырсақ.
Лагранж теңдеулерін экстремальдық әсер принципі бойынша қорытып шығару үшін (2. 2) -шарттың орындалуының жеткілікті екенін дәлелдесек болғаны. Ол үшін жоғарыдағы 2. 3-суретте көрсетілген АСВ шын орын ауыстыруынан басқа, осыған жақын жатқан АС'В ықтималдық орын ауыстыруды қарастырайық. Сонда δS әсер функциясының өсімшесін былай табуға болады;


Бұл Лагранж теңдеулері. Экстремальдық әсер принципінен мынандай маңызды салдар шығады: Механикалық жүйенің Лагранж функциясы жалпыланған координаттарға және уақытқа тәуелді болатын кез келген функциядан уақыт бойынша алынған туындыдай дәлдікпен анықталады. Шынында да, бір механикалық жүйенің L (q, q, t) және L (q, q, t) екі Лагранж функциясын қарастырайық, олар бір-бірімен мынандай байланыста болсын,
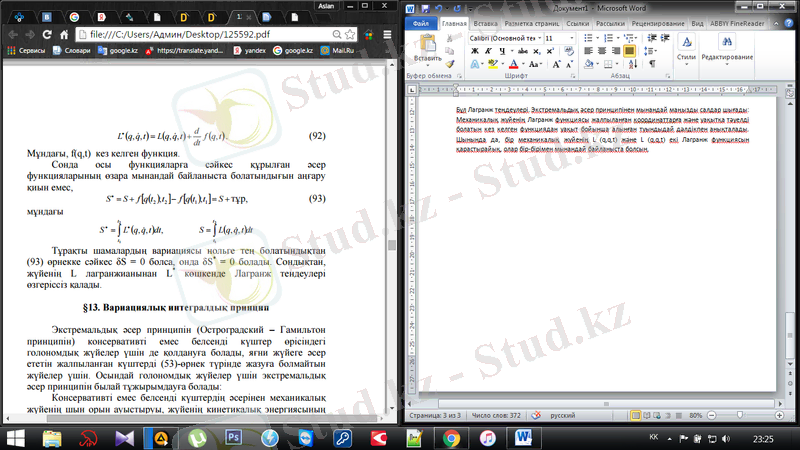
Мұндағы, f(q, t) кез келген функция. Сонда осы функцияларға сәйкес құрылған әсер функцияларының өзара мынандай байланыста болатындығын аңғару қиын емес,

мұндағы

Тұрақты шамалардың вариациясы нольге тең болатындықтан (93) өрнекке сәйкес δS = 0 болса, онда δS * = 0 болады. Сондықтан, жүйенің L лагранжианынан L * көшкенде Лагранж тендеулері өзгеріссіз қалады.
2. 2 Вариациялық интегралдық принцип
Экстремальдық әсер принципін (Остроградский - Гамильтон принципін) консервативті емес белсенді күштер өрісіндегі голономдық жүйелер үшін де қолдануға болады, яғни жүйеге әсер ететін жалпыланған күштерді (53) -өрнек түрінде жазуға болмайтын жүйелер үшін. Осындай голономдық жүйелер үшін экстремальдық әсер принципін былай тұжырымдауға болады: Консервативті емес белсенді күштердің әсерінен механикалық жүйенің шын орын ауыстыруы, жүйенің кинетикалық энергиясының вариациясымен барлық белсенді күштердің виртуалды жұмыстарының қосындысынан алынған интеграл нольге тең болуына сәйкес келеді, яғни
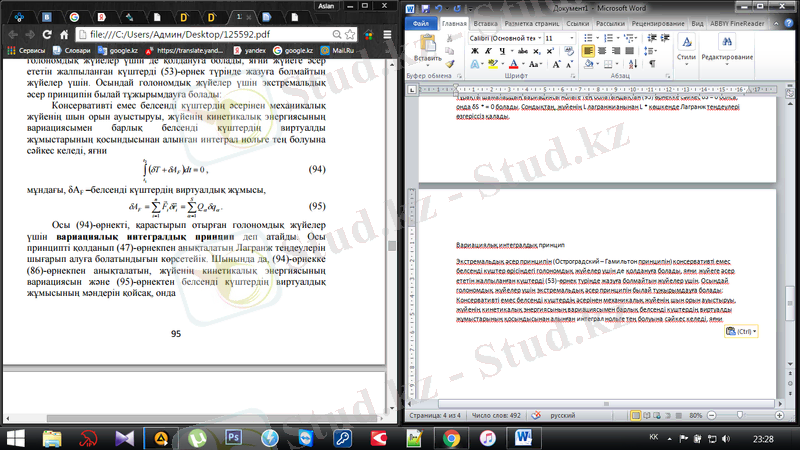 (2. 3)
(2. 3)
мұндағы, δА -белсенді күштердің виртуалдық жұмысы,
 (2. 4)
(2. 4)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz