Леонард Эйлер циклы

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе

: 1

Кіріспе: Леонард Эйлер

3: 4

: 1. 1

Кіріспе: Байланысқан және байланыссыз графтар

3: 5

: 2

Кіріспе: Эйлер циклы

3: 11

Кіріспе: Қорытынды

3: 18

Кіріспе: Қолданылған әдебиеттер тізімі

3: 19

КІРІСПЕ

Дискреттік Математика - математиканың дискретті құрылымдардың қасиеттерін зерттейтін саласы. Мұндай құрылымдарға шектеулі топтар, шектеулі графтар, сондай-ақ, ақпаратты түрлендіргіш кейбір математикалық модельдер, шектеулі автоматтар, Тьюринг машинасы, және т. б. жатады. Компьютерлерді жасау және пайдалану программалау тілдері, ақпаратты өңдеу және тарату жабдықтары, автоматтандырылған басқару және жобалау жүйелері мамандарының зерттеу жұмыстары үүшін дискретті математика әдістері негізгі құрал, ал дискретті математика тілі осы мәселелер бойынша пайдаланатын ғылыми және техникалық тіл болып табылады. - программалау процесінде жасанды интеллект есептерін шығаруда, программалардың дұрыстығын дәлелдеуде модельдеуді пайдалануға дағдыландыру. Компьютерлік ғылымның теориялық фундаменті болып саналатын дискретті математика арқылы сипаттағы құрылымдар қасиеттерін зерттейтін математиканың бір саласы болып саналады.

Дискретті математика негіздері егер үлкен есептеу жүйелері құрылса, онда олардың қандай да бір пайда болған үлкен есептерді шешу үүшін қажеттілігі болғаны. Кез-келген салада әр түрлі мәселелер, яғни соған байланысты жүздеген, мыңдаған сұрақтар пайда болуда. Ал олардың жауабын іздеудің жалпы қағидалары өте ертеректе құрастырылған. Бірінші, осы объектінің немесе процестің математикалық моделін құрудан бастайды. Математикалық модельдеу объектінің белгілі бір болмысын немесе болып жатқан процестерді теңдеулер тілінде және басқадай математикалық құралдар арқылы көрсету. Яғни, математикалық модель зерттеу облысына қатысты қандай да бір дифференциалдық, интегралдық алгебралық немесе басқа да бір өрнектер жиыны. Осы алынған математикалық модельді, яғни теңдеудінемесе әртүрлі теңдеулер жүйесін шеше отырып, біз қойылған сұрақтардың жауабын ала аламыз. Әрине, компьютерлер қаншалықты қуатты болғанымен олар өз беттерінше берілген есептерді шеше алмайды. Олар тек қана өте қарапайым амалдарды ғана орындай алады. Ал олардың бүкіл интеллектуалдық күші адам құрастырған бағдарламалармен анықталады. Бағдарламалар қандай да бір мақсатқа құрылған қарапайым амалдар тізбегін іске асырады. Шешімді іздеу, қарапайым амалдар тізбегін орындау процесіне келіп тіреледі. Бұл алгоритмді құрастыру деп аталады. Дискретті математика және математикалық логика пәні математика білімінің бөлінбес бір бөлігі болып саналады.

1 Леонард Эйлер

Леонард Эйлер швейцариялық математик, механик және физик. Базель университетін бітірген. 1727 жылдан Санкт-Петербург академиясында қызмет істеді. Ол Санкт-Петербург және Бердин академияларынан басқа Париж академиясының, Лондон корольдік қоғамының, Санкт-Петербург академиясының т. б көптеген ірі ғылым қоғамдардың мүшесі болды.

Эйлердің негізгі еңбектері сол кездегі математика мен механиканың барлық саласына, серпімділік теориясына, математикалық физикаға, оптикаға, музыка теориясына, машиналар теориясына, баллистикаға, теңіз ғылымына, т. б. арналған. Оның ғылыми еңбектерінің жинағы ауқымды 60-80 том көлемінде деп болжанады. Эйлер “Аналитикалық түрде баяндалған механика не қозғалыс туралы ғылым” (2 томдық, 1736), “Анализге кіріспе” (2 томдық, 1748), “Дифференциалдық есептеу” (1755), “Универсал арифметика” (2 томдық, 1768 - 1769) және 6 тілде 30 шақты рет басылып шыққан “Интегралдық есептеу” (3 томдық, 1768 - 1770; 4 томдық, 1794), т. б. осы сияқты бірқатар классик. монографияларында өзінің және басқа ғалымдардың зерттеулерінің нәтижелерін жүйеге келтірді.

Ол “Механика” атты монографиясында жаңа математикалық анализдің көмегі арқылы нүкте динамикасын тұңғыш рет кең көлемде баяндады, ал “Қатты денелер қозғалысы теориясында” қатты дененің кинематикасы мендинамикасының теориясын жетілдірді және қатты дененің қозғалмайтын нүкте маңынан айналу теңдеуін (гироскоптар теориясының бастамасы болған) тапты. Аспан механикасы бойынша да үлкен жаңалықтар ашты.

1771-1757 жылдары жарық көрген мемуарлары тұтас орта механикасы жөнінен жүргізілген зерттеулерге қосылған елеулі үлесі болды. Эйлер вариациялық есептеу мен дифференциалдық теңдеулер теориясының негізін жасады, дифференциалдық және интегралдық есептеулерді жалпылап, одан әрі дамытты. Ол - 886 мақала мен мемуардың

авторы.

Математик, механик Л. Эйлер байланысқан бағытталмаған мультиграфта оның барлық қабырғаларынан тұратын цикл болатынын тұжырымдап берді. Мультиграфтың барлық қабырғаларынан тұратын цикл Эйлерлік д. а.

Теорема. Байланысқан бағытталмаған мультиграф Эйлерлік болады сол жағдайда, егер оның әр төбесінің дәрежесі - жұп сан болса.

Эйлерлік мультиграфта эйлер циклін табудың алгоритмі:

кез келгенатөбені аламыз.
атөбесіне инцидентті кез келгенuқабырғаны алып, оған1номер береміз (бұл қабырғаны жүрілген д. а. )
әрбір жүрілген қабырғаны сызып, 1ден артық номер беріп отырамыз.
хтөбесінде тұрыпатөбесімен қосатын қабырғаны таңдамаймыз, егер басқа мүмкіндік болатын болса.
хтөбесінде тұрып, сызылған қабырғаны таңдамау керек.
графтың барлық қабырғасы номерленгеннен кейін эйлер циклі пайда болады. Реттелген номер графтың айналу ретін көрсетеді.

1. 1 Байланысқан және байланыссыз графтар

Графтағы ешбір қабырға арқылы 1 -ден артық рет өтпейтін сызық шынжыр деп аталады. Егер қозғалысты А нүктесінен бастап, барлық төбелерден әр қабырға бойымен тек бір ғана рет жүре отырып, сол А төбесіне қайта оралу мүмкін болса, мұндай жолды цикл деп атайды. Егер циклдың барлық төбелері әртүрлі болса, мұндай цикл қарапайым цикл, ал қарсы жағдайда - қарапайым емес цикл деп аталады. Кей жағдайда цикл графтың барлық қабырғаларын дәл бір реттен қамтиды. Мұндай циклдарды Эйлер сызықтары деп атайды.

Егер графтың кез келген екі төбелері қандай да бір шынжырмен байланысып тұрса, ондай графты байланысты граф дейді, яғни байланысты граф дегеніміз бірде бір оқшауланған нүктесі болмайтын граф.

Егер графтың ең болмағанда екі төбесін қосатын жол болмаса, оны байланыссыз граф деп атайды, яғни оның қандай да бір төбесінен шығып, басқа төбелеріне қабырғаларының ешқайсысынан бір рет қана өте отырып бару мүмкін болмайды.

Байланысты графтың қасиеттері:

1. кез келген байланысты графтың дәрежелері тең болатын ең болмағанда екі төбесі бар болады.

2. барлық төбелерінің дәрежелері жұп болатын байланысты граф Эйлер сызығы болып табылады.

3. байланысты графта оның барлық қабырғаларын дәл бір реттен қамтитын l(A, B) шынжыры бар болуы үүшін А мен В төбелерінен басқа тақ дәрежелі төбелердің болмауы қажетті және жеткілікті.

Барлық қабырғаларының бағыты көрсетілген граф бағдарланған граф деп аталады. Қабырғаларының бағыты көрсетілмеген графты бағдарланбаған граф дейді. Кей қабырғаларының бағыты бар, ал кей қабырғаларының бағыты көрсетілмеген графты аралас граф дейді.

Ұштарындағы нүктелері беттесетін қабырғаны тұзақ деп атайды. Графты кескіндеу барысында тұзақ сол төбеге қайтып келетін және басқа төбелерден өтпейтін тұйық доға түрінде болады.

Эйлера функциясы 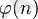$\varphi(n)$ , мұндағы - натурал сан, санынан үлкен емес әрі онымен өөзара жай натурал сандар санына тең. Эйлера бұл функцияны сандар теориясы еңбектерінде алғашқы болып пайдаланғандықтан соның құрметіне осылай талып кетті.

Анықтама

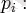$p_i:\,$ жай сандарға келесідей жіктелген $n\,$ натурал саны берілсін:

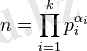
$n = \prod_{i=1}^k p_i^{\alpha_i}$

Онда

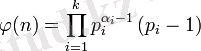
$\varphi(n) = \prod_{i=1}^k p_i^{\alpha_i - 1} \left( p_i - 1 \right)$

функциясы Эйлер функциясы деп аталады. Мұндағы 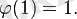$\varphi(1) = 1.$ болады деп саналады. Эйлера функциясын Эйлер көбейтіндісі ретінде де өрнектеуге болады:

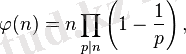
$\varphi(n)=n\prod_{p\mid n}\left(1-\frac{1}{p}\right),$

мұндағы 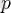- санының жай сандарға жіктелуінде қатысатын барлық жай сандарды қабылдайды.

Функцияның кейбір мәндері

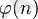
$\varphi(n)$

: 0+

+0:

+1: 1

+2: 1

+3: 2

+4: 2

+5: 4

+6: 2

+7: 6

+8: 4

+9: 6

: 10+

+0: 4

+1: 10

+2: 4

+3: 12

+4: 6

+5: 8

+6: 8

+7: 16

+8: 6

+9: 18

: 20+

+0: 8

+1: 12

+2: 10

+3: 22

+4: 8

+5: 20

+6: 12

+7: 18

+8: 12

+9: 28

: 30+

+0: 8

+1: 30

+2: 16

+3: 20

+4: 16

+5: 24

+6: 12

+7: 36

+8: 18

+9: 24

: 40+

+0: 16

+1: 40

+2: 12

+3: 42

+4: 20

+5: 24

+6: 22

+7: 46

+8: 16

+9: 42

: 50+

+0: 20

+1: 32

+2: 24

+3: 52

+4: 18

+5: 40

+6: 24

+7: 36

+8: 28

+9: 58

: 60+

+0: 16

+1: 60

+2: 30

+3: 36

+4: 32

+5: 48

+6: 20

+7: 66

+8: 32

+9: 44

: 70+

+0: 24

+1: 70

+2: 24

+3: 72

+4: 36

+5: 40

+6: 36

+7: 60

+8: 24

+9: 78

: 80+

+0: 32

+1: 54

+2: 40

+3: 82

+4: 24

+5: 64

+6: 42

+7: 56

+8: 40

+9: 88

: 90+

+0: 24

+1: 72

+2: 44

+3: 60

+4: 46

+5: 72

+6: 32

+7: 96

+8: 42

+9: 60

Қасиеттері

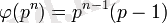$\varphi(p^n)=p^{n-1}(p-1)$ , егер 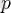- жай сан болса. Жекеше түрі: n=1 болғанда

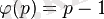$\varphi(p)=p-1$ ;

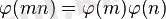$\varphi(mn)=\varphi(m)\varphi(n)$ , егер m мен өөзара жай болса. Яғни Эйлер функциясы мультипликативті;

$a^{\varphi(m)}\equiv 1\pmod m$ , егер m мен өөзара жай болса. Бұл Эйлер теоремасы

болып табылады;

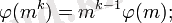
$\varphi(m^k)=m^{k-1}\varphi(m);$

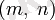$mn=(m,\;n)[m,\;n], \varphi(m)\varphi(n)=\varphi((m,\;n))\varphi([m,\;n]), \varphi(mn)\varphi((m,\;n))=\varphi(m)\varphi(n)(m,\;n)$ егер $[m,\;n]$ - Ең Кіші Ортақ Еселік, aл $(m,\;n)$ - Ең Үлкен Ортақ Бөлгіш.

Асимптоталық байланыстар

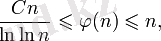$\frac{Cn}{\ln\ln n}\leqslant\varphi(n)\leqslant n,$ мұндағы - белгілі бір тұрақты;

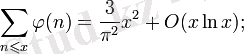
$\sum_{n\leqslant x}\varphi(n)=\frac{3}{\pi^2}x^2+O(x\ln x);$

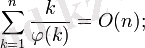
$\sum_{k=1}^n\frac{k}{\varphi(k)}=O(n);$

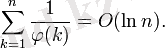
$\sum_{k=1}^n\frac{1}{\varphi(k)}=O(\ln n).$

Аналитикалық байланыстар

Эйлер функциясы Мёбиус функциясымен де байланысы бар:

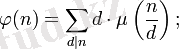
$\varphi(n)=\sum_{d\mid n} d\cdot\mu\left(\frac{n}{d}\right);$

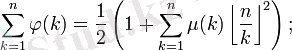
$\sum_{k=1}^n\varphi(k)=\frac{1}{2}\left(1+\sum_{k=1}^n \mu(k)\left\lfloor\frac{n}{k}\right\rfloor^2\right);$

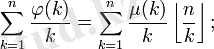
$\sum_{k=1}^n\frac{\varphi(k)}{k}=\sum_{k=1}^n\frac{\mu(k)}{k}\left\lfloor\frac{n}{k}\right\rfloor;$

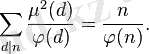
$\sum_{d\mid n}\frac{\mu^2(d)}{\varphi(d)}=\frac{n}{\varphi(n)}.$

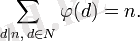
$\sum_{d\mid n,\; d\in N}\varphi(d)=n.$

Дирихле қатарын 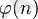$\varphi(n)$ коэффициенттерімен Риман дзета-функциясы арқылы өрнектеуге болады:

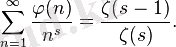
$\sum_{n=1}^\infty\frac{\varphi(n)}{n^s}=\frac{\zeta(s-1)}{\zeta(s)}.$

Ламберт қатары қосындысын 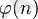$\varphi(n)$ коэффициенттерімен:

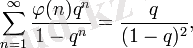
$\sum_{n=1}^\infty\frac{\varphi(n)q^n}{1-q^n}=\frac{q}{(1-q)^2},$

мұндағы |q|<1 .

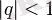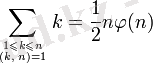$\sum_{1\leqslant k\leqslant n\atop(k,\;n)=1}k=\frac{1}{2}n\varphi(n)$ мұндағы n>1 .

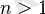Компьютерлік іске асырылуы

Си тілінде

Төмендегі функция 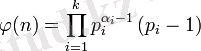$\varphi(n) = \prod_{i=1}^k p_i^{\alpha_i - 1} \left( p_i - 1 \right)$ көбейтіндісін есептейді. Бұл санын жай сандарға көбейткіштерге 2-ден бастап барлық сандарға бөлу арқылы іске асырылады; егер санға бөлінсе, бұл сан санын өшіріледі, ал нәтиже-көбейтінді сәйкесінше сол санға көбейтіліп өседі.

int phi(int n)

{

int ret = 1, p;

for(p = 2; p * p <= n; p++)

{

if (n % p == 0)

{

n /= p;

while(n % p == 0)

{

n /= p;

ret *= p;

}

ret *= p - 1;

}

return n > 1 ? ret * (n - 1) : ret;

}

VB. Net

Private Function phi(ByVal n As Integer) As Integer

Dim ret As Integer = 1, p As Integer = 2

For p = 2 To n / p

If n Mod p = 0 Then

n /= p

While n Mod p = 0

n /= p

ret *= p

End While

ret *= p - 1

End If

Return If(n > 1, ret * (n - 1), ret)

End Function

Айталық m = p11p22 … ptt, m>1натурал саныны Канонды жіктелуі болсын. (m) = p11-1(p1-1) p22-1(p2-1) …ptt -1(pt-1) жне (1) = 1 болсын. Сонымен натурал аргументті функциясын анықтаймыз.

Анықтама 1 Жоғарыда көрсетілген әдіспен аныталған функциясы Эйлер функциясы деп аталады.

Анықтама 2 Эйлер функциясы n-нан кіші жне n-мен өөзара жай бүтін сандарды санына функцияны атайды. Функция (n) деп белгіленеді.

Мысала (10) = 4. Эйлер функциясыны келесі тамаша қасиеті бар: егер n = pq, мұндаы p және q - жай сандар, онда (n) = (p-1) (q-1) -ге те болады.

Теорема 1 (Эйлер) Кез-келген n модулі мен n-мен өөзара жай а саны үүшін келесі салыстыру a(n) -1 1(mod n) .

Анықтама 3 Келесі ш шартты қанағаттандыратын функциясын мультипликативті деп атаймыз:

1) кез келген натурал сан үүшін анықталған;

2) (1) = 1;

3) егер (a, b) = 1 болса, онда (ab) = (a) (b) .

Теорема 2 Эйлер функциясы - мултипликативті функция.

Дәлелдеуі. Айталық p11… ptt жне q11 … qss сәйкесінше өөзара жай натурал m1>1 жне m2>1 өөзара жай сандарыны канонды жіктеулері болсын.

Онда p1, …, pt сандарыны әрқайсысы q1, …, qs сандарыны әрқайсысына өзгеше. Бұдан m1m2 канонды жіктеуі p11… ptt q11…qss. (m1m2) = (m1) (m2) тедеуі, Эйлер функциясыны анықтамасынан тікелей шығады. m1 = 1 немесе m2 = 1 үүшін берілген теңдеу дайын. Теорема дәлелденді.

Теорема 3 (m) саны 1, 2, …, m санды тізбегіндегі m-мен өзара жай болатын сандарды санына те.

Дәлелдеуі. Дәлелдеме m>1 саныны канонды жіктеуіндегі жай көбейткіш сандарды саны n бойынша математикалы индукция әдісі бойынша жүргізіледі. Теорема n = 0 (m = 1) жне n = 1 (m = p) үшін орындалады, мұндағы p - жай сан. Айта кетерлік жайт, i натурал саны mp-мен өзара жай болу үшін ол бір мезгілде m мен p сандарымен өзара жай болуы қажет және жеткілікті. 1, 2, …, mp тізбегін талдау үшін ұзындыы m-ге те p тізбекшелеріне mk+1, mk+2, …, mk+m-бөлеміз, мнда k = 0, 1, …, p-1. Теорема 3-тен (mk + i, m) = (i, m) шығады. Осы теңдік пен осы индуктивті қайарымнан mk+1, mk+2, …, mk+m тізбекшесінде m-мен өзара жай (m) сан бар. Осыдан 1, 2, …, mp тізбегінде m-мен өзара жай (m) p сан бар. M p-а бөлінетін жағдайда, бұл сандар p-мен өзара жай, сонымен қатар mp санымен де өзара жай. Соны ескерту мен дайын тедік (mp) = (m) p қарастырылан жадайда теореманы айарымын дәлелдейді.

m-ні p-а бөлінбейтін жадайын арастыру алды. m-мен өзара жай (m) p сандарыны санынан осыларды p-а бөлінетіндеріні санын алып тастаса, іздеген (mp) санын табамыз. Ол сандар тек p, 2p, 3p, …, mp сандарыны арасында ғана болуы мүмкін. Сондытан, m-мен өзара жай сандарды арасындаы p-а бөлінетіндері саны p, 2p, 3p, …, mp сандарыны арасындаы m-мен өзара жай сандарды санына тең болады. Егер im жне (m, p) = 1 болғанда (ip, m) = (i, m) болатынын ескерсек, онда p, 2p, 3p, …, mp сандарыны арасындағы m-мен өзара жай сандар саны. 1, 2, …, m сандарыны арасындағы m-мен өзара жай сандар санына те, яғни индукция бойынша (m) . қорыта келе, ізделінді (mp) = (m) p - (m) = (m) (p-1) . Теорема дәлелденді.

Эйлер функциясыны осы қасиетіні берілген дәлелдемесін Р. А. Сүйіндіков сынды.

Мысалдар: Берілген n натурал саны жай сан деп саналады, егер де ол тек өзіне ғана және 1-ге бөлінетін жағдайда a, n 2 натурал сандар өзара жай сандар деп саналады, егер оларды орта бөлгіштері болмаса.

1. n = 7

1 2 3 4 5 6 j(7) = 6.

2. n = p*q, p, q -жай сандар, j(n) = (p-1) *(q-1)

n = 33 = 11*3, j(33) = (11-1) (3-1) = 20.

3. n = kr

j(n) = (k-1) *kr-1, n = 8 = 23

j(8) = (2-1) *23-1 = 1*4 = 4.

2 Эйлер циклы

Графтар теориясына негіз болған есептердің бірі Кенигсберг көпірлері туралы есеп. 1-Суретте Леонард Эйлердің тұсындағы (17 ғасыр) XVII ғасырдағы Кенигсберг қаласының картасы салынған. Қала Прегель өзенінің екі жақ жағалауында және 2 аралда. орналасқан Аралдар өөзара және жағалаулармен 7 көпірмен жалғасқан. Кенигсберг тұрғындарының арасында сол кезде Кенигсберг көпірлері деп аталатын есеп кең тараған:

Есеп . Үйден шығып әр көпірмен бір рет қана жүріп үйге қайтып келуге болама ма деген сұрақ туады?

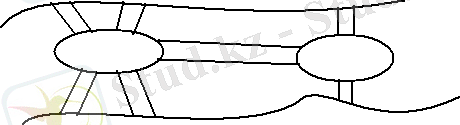
Сурет 1

Бұл есеп үүшін көпірлерден өтудің маңызы бар. Сондықтан көпірлердің орналасуын 2-суреттегі бағытталмаған мультиграфпен алмастыруға болады. Бұл графта Б, В төбелері өзеннің жағаларына, ал А, Г төбелері аралдар, ал мультиграфтың қабырғалары көпірлерге сәйкес келеді. Егер G графында оның барлық қабырғалары арқылы өтетін цикл табылса Кенигсберг туралы есеп шешілді деп есептеледі (Цикл деп бірде бір қабырға қайталанбайтын циклды маршрутты айтатынын еске саламыз) . Демек графтар тілінде есептін қойылуы төмендегідей: Мультиграфта оның барлық қабырғалары болатындай цикл бар ма? Атақты ғалым-математик Л. Эйлер байланысты, бағытталмаған мультиграфта оның барлық қабырғалары болатындай цикл болудың шартын анықтап дәлелдеп берді.

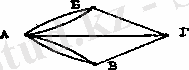
Сурет 2

Теорема Байланысты бағытталмаған мультиграфтың әр төбесінің дәрежесі жұп сан болса ғана Эйлер циклы болады.

Анықтама. Мультиграфтың барлық қабырғалары болатын цикл Эйлер циклы деп, ал Эйлер циклы бар граф Эйлер графы деп аталады. Жоғардағы суреттегі мультиграфта Эйлер циклы жоқ, себебі онда дәрежесі тақ төбе бар. Айталық ондай цикл бар деп жориық. Олай болғанда бұл циклдың бойымен жүре отыра графтың кез келген төбесіне одан шығу қанша болса сонша рет кіреміз. Демек, G графының әр төбесінің дәрежесі жұп болуы керек. G графында керісінше барлық төбелер тақ дәрежелі.

Бұл тұжырым кез келген бағытталған G графына да жарамды. Сонымен бағытталмаған G графында оның барлық қабырғалары арқылы өтетін цикл бар болу үүшін G графының төбелерінің дәрежесі жұп болуы қажетті.

Анықтама. Бағытталмаған (бағытталған) G графындағы цикл оның барлық қабырғалары арқылы өтсе, ол- Эйлер циклы деп аталады. Бағытталмаған графта Эйлер циклы бар болу үүшін бұл графтың байланысты болуы қажетті.

Анықтама. Кез келген х, у∈V(G) төбелерін қосатын жол бар болса бағытталмаған G графы байланысты граф деп аталады.

Анықтама . Егер С циклы Бағытталмаған G графының барлық қабырғалары арқылы өтетін болса, кез-келген х, у V(G) төбелері үүшін C циклының х төбесінен у төбесіне апаратын C(x, y) кесінәдісі х-тен у-ке апаратын жол болып табылады. Олай болса G байланысты. Эйлер циклының бар болуы үүшін графтың дәрежелерінің жұп болуы және оған қоса графтың байланысты болуы жеткілікті екен.

Эйлер теоремасы. Бағытталмаған графта Эйлер циклы болу үүшін оның байланысты болуы және оның барлық дәрежелерінің жұп болуы қажетті және жеткілікті.

Эйлер теоремасын шамалы өзгеріспен бағытталған графтарға да қолдануға болады. Ол үүшін бағытталған графтардың да байланысты болу ұғымын енгізу керек.

Доғаларының бағыттарын алып тастағаннан кейінгі алынған бағытталмаған G графы байланысты болса, бағытталған °G графы байланысты деп аталады.

Теорема . Бағытталған G графында Эйлер циклы болу үүшін оның әр төбесіне кіретін дәрежемен шығатын дәрежелердің бірдей болуы қажетті және жеткілікті. дәр. +(х) = дәр. - (х) барлық x∈V(G) .

Байланысты және тиелген бағытталмаған графтағы белгіленген V ₀ және Vn төбелерін қосатын ең қысқа жолды іздеуді жүзеге асыратын Форд алгоритмі.

V ₀ төбесіне λ ₀ таңбасы беріледі де, қалған төбелердің таңбалары λ=∞V ₀ болады.

(Vi, Vj) қабырғаларының ішінен λ _j - λ _i >L((V _i , V _j ) ) орындалатындай қабырғалар ізделеді және олардың λ _j индекстері λ _j '=λ _i +L((V _i , V _j ) ) алмастырылады. Индекстрді өзгерту процесі одан әрі λj таңбасын азайту мүмкіндігі болмайтын бірде бір қабырға қалмағанша жүргізіледі. Нәтижесінде әр төбенің таңбасы осы төбенің V ₀ төбесіне дейінгі ең қысқа қашықтықты көрсетеді. Ең қысқа жолдың өзін табу үүшін Vn төбесінен екі жағындағы төбелердің таңбаларының айырымы қабырғаның ұзындығына тең қабырғалардың бойымен қозғалу қажет.

ХХ ғасырдың бас кезінде жиын теориясында қайшылықтар табылды. Бұл қайшылықтар математиктерді қатты толғандырып, олардың алдарына үлкен мәселе қойды. Осы мәселені шешу жолында математиктердің алдында мынандай сұрақтар туды: «теорема» деген не, «дәлелдеу» деген не? Немістің атақты математигі Д. Гильберт программа жариялады. Осы программа бойынша барлық математиканы былай құру керек:

Математиканың тілін дәл анықтау керек.
Аксиомаларды беру керек.
Дәлелдеудің дәл анықтамасы берілуі керек.

Осындай системаларды формальдық система дейді. Оларды зерттейтін ғылымды математикалық логика деп атайды. Гильберттің ойынша бұндай формальдық системада қайшылық деген ұғымды дәл анықтауға, содан кейін бұл системаның қайшылықсыз екендігін дәлелдеуге болады. Математикада жоғарыда аталған система құрылып, бұл системалардың қайшылықсыздығын дәлелдеу қиынға соқты. Осы айтылған ең негізгі, түйінді қиыншылық болып шықты. Оны 1931 жылы Гедельдің екі атақты теоремасы шешті. Егер формальдық система қайшылықсыз болса, онда бұл қайшылықсыздықты осы формальдық системаның ішінде дәлелдеуге болмайды. Бұл, Д. Гильберт ойлағандай болмай, оның программасы тұйыққа тірелді. Бірақ бұл программа математикада үлкен орын алады. Формальдық системалар математиканың негізін зерттеуде, аксиоматикалық әдістің маңызын зерттеуде елеулі табыстарға жетті.

Дискретті математика математика аймағының қасиеттерін зерттейді.

Дискретті математика компьютерлік техниканың қарқынды дамуымен байланысты, яғни ақпаратты тасымалдау мен өңдеу тәсілдерінің қажеттігінен, әртүрлі модельдерді компьютерде беруінен көрінеді. Бұл жоғарыда айтқан математиканың соңғы сипатындағы сұлбалары.

Дискретті математика :

формальды елестетудің әмбебап тілі;
ақпаратты тиімді ауыстыру тәсілі;
бір тілден екінші тілге көшкенде модельдің мазмұнды сақтап қалу шарты мен мүмкіндігін береді.