Логикалық функцияларды минимизациялау және комбинациялық схемаларды синтездеу: Квайна-МакКласки және Вейч-Карно әдістері


МАЗМҰНЫ
Логикалық функцияны сипаттайтын логикалық өрнекке лайық, осы логикалық функцияның қызметін атқаратын элементар (қарапайым) схемаларды анықтау. Ол үшін логикалық өрнекті тиімді жүктеп, оның әрбір мүшесі қарапайым схемаға лайықты және алынған схемалар саны ең аз (минимальды) болатындай түрге түрлендіру. Логикалық алгебра тәсілдері схемаларды талдау және құрастыру есептерінен басқа информацияны өңдеу процестеріне де қолданылады.
Бір немесе бірнеше қарапайым айтылымдардан күрделі айтылымдар құрастыруға болады. Қарапайым айтылымдардан күрделі айтылым құрастыруға логикалық байланыс таңбалары қолданылады.
Айтылымдар арасындағы логикалық байланыстар екілік айнымалыларға қолданылатын амалдар операциялар түрінде беріледі.
Электронды есептеу машиналарының цифрлы өлшеуіш аспаптарының өндірістік автоматты қондырғылардың негізінде логикалық элементтер деп аталатын қарапайым тізбектер жатады. Бұл тізбектерде ескерілетін шама - олардың кірмесі мен шықпасындағы кернеулердің бары не жоғы немесе олардың потенциалдық деңгейлері. Кернеудің бары немесе жоғары деңгейі «1» деп, ал оның төменгі деңгейі «0» деп алынады осы себепті де жоғарыда аталған құрылғыларда екілік санау жүйесі қолданылады. Екілік санау жүйесін қолдану «Емес», «және», «немесе» деп аталатын қарапайым үш түрлі тізбекті барлық логикалық және цифрлық құрылғылардың негізіне алуға мүмкіндік береді.
«Емес» логикалық элементі пайымдалған тұжырымды теріске шығару операциясын орындайды. Мұны логикалық алгебрада A=
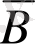 деп жазады да, «А деген В емес» деп оқиды. Ендеше нөлді бірлік теріске шығарады (
деп жазады да, «А деген В емес» деп оқиды. Ендеше нөлді бірлік теріске шығарады (
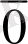 =1) да, ал бірлікті нөл теріске шығарады (
=1) да, ал бірлікті нөл теріске шығарады (
 =0) . 1-суретте «Емес» логикалық элементін транзистордың көмегімен орындау схемасы келтірілген.
=0) . 1-суретте «Емес» логикалық элементін транзистордың көмегімен орындау схемасы келтірілген.
+Ек А
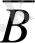 күй кесте
күй кесте
0 1 A
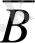
- 0
Rk б) в) шартты
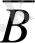 +E +E белгі
+E +E белгі
А К R υш
νа R νв R υш
В г)
а)
1
1 сурет. «Емес» логикалық элементінің схемасы (а) мен күй кесте (б) және шартты белгісі.
Егер, кірмеге кернеу берілсе (А=1), онда транзистор ашылады да қорек көзінің кернеуі түгел дерлік R, резисторына түседі. Сондықтан шықпада кернеу нөлге тең деп алуға болады. В=0 кірмелік сигнал жоқ кезде (А=0) транзистордың кедергісі R 1 резисторының кедергісінен әлдеқайда көп болатындықтан шықпаның кернеуі шамамен қорек көзінің кернеуіне те болады, яғни В=1. былайша айтқанда «А бар болса В жоқ, А жоқ болса В бар».
«Және» элементі (2, а-сурет)
+Е
Rk υc
C
R1
A νT1
R2
B νT2 A
B C
υВ υА
а)
в) шарт белгі
б) күй кесте
2 сурет. «Және» элементінің электрлік схемасы (а) мен күй кестесі (б) және шартты белгісі (в) .
С=А×В логикалық көбейту амалын орындайды. Бұл «С айтылымы дұрыс, егер А және В айтылымдары дұрыс болса» деген ұғымды білдіреді. Басқаша айтқанда «С бар егер А да және В да бар болса». Шықпалық кернеу νТ1 және νТ2 транзисторлары ашық болғанда ғана пайда болады. Ал транзисторлардың екеуі де ашық болуы үшін А және В кірмелерінің екеуіне де сигнал беру керек. Күй кестесінен көрініп тұрғандай С=1, егер А=1 және В=1 болса. Басқа жағдайлардың барлығында да С=0.
«Немесе» элементі С=А+В логикалық қосу амалын орындайды. Бұл С айтылымы дұрыс, егер А айтылымы дұрыс болса немесе В айтылымы дұрыс болса» деген ұғымды білдіреді. Басқаша айтқанда С, егер А бар болса немесе В бар болса», «немесе» элементін диодтардың көмегімен құрған тізбекте С10, Н0 а-сурет) шықпалық кернеу кірмелердің біреуіне немесе екеуіне де кернеу берген жағдайда пайда болады.
Тізбектің күй кестесінен көрініс тұрғандай С=1, егер А=1 де В=1 немесе А=1 де В=0 немесе А=0 де В=1, ал С =0, егер А =0 және В=0 болса.
Қарастырылған логикалық элементтерден басқа екі немесе одан да көп амал дарды орындайтын «немесе -емес» «және емес» деп аталатын элементтер де кеңінен қолданылады. «Немесе-емес» элементінің электрлік схемасы, күй кестесі және шартты белгісі 10-41 суретте келтірілген.
Кірмелерінде сигнал жоқ кезде транзистор жабық болатындықтан оның шықпасындағы кернеу шамамен керек көзінің кернеуіне жуық болады, яғни А=0 және В=0 болса ғана С=1.
Егер кірменің біреуіне немесе екеуіне де кернеу берілсе, онда трназистор ашылады да, шықпасында кернеу шамамен нөлге тең болады, яғни С=0, егер А=1, В=1 немесе А=0, В=0 немесе А=0, В-0 немесе А=0 В=1 болса.
1 Математикалық логиканың негізгі функциялары
ЦЕМ қарапайым амалдарды орындайтын бөлек элементтерден құралады. Элемент - ол әдетте электрондық схема. ЦЕМ-нің барлық элементтерін атқаратын қызметтеріне байланысты топтарға бөлуге болады: логикалық, есте сақтаушы, күшейтетін және арнайы элементтер. Логикалық элементтерден, арифметикалық және басқа амалдарды қамтамасыз ететін амалдар схемасын құрайды. «Логикалық элемент» деп аталу себебі, жеке дара элементтің анықталған байланысты жүзеге асыруына мүмкіншілік беруінде немесе жеке логикалық функцияларды орындауында. Кейбір аса маңызды функцияларды және оларды іске асыратын логикалық элементтерді қарастырайық.
Логикалық функция «ЖӘНЕ». Коньюнкция (бірігу) - «ЖӘНЕ» логикалдық функциясы. Екі (немесе одан да көп) пікірлер бір күрделі пікір болып бірігуі мүмкін. Ақиқат болатын, екі пікірдің коньюнкциясын күрделі пікір дейміз, егер құрамдас екі пікірде ақиқат болса, және жалған егер құрамдас пікірдің ең болмаса біреуі жалған болса. Күрделі пікір: «Ол оған келді, және олар болашақ туралы әңгімелесті» тек сонда ғана ақиқат, егер құрамдас пікірлердің екеуі де ақиқат болса: 1- ол оған келді және 2- олар болашақ туралы әңгімелесті. Пікірлердің ең болмағанда біреуі жалған болған жағдайда, күрделі пікірде жалған болады. Коньюнкцияны «ЖӘНЕ» логикалық функциясы деп атайды. Жоғарыда көрсетілген мысал «ЖӘНЕ» шылауының атқаратын міндетін көрсетеді. Ақиқат пікірді (1) бірмен, ал жалған пікірді нольмен (0) белгілейік. Екі пікірдің конюнкциясын «&» немесе «^» таңбаларымен белгілейік. Екі пікірдің коньюнкциясын логикалық көбейту ережесімен жазуға (табуға) болады:
0*0=0 (екі пікірде жалған және күрделі пікірде жалған) ;
0*0=0 (бірінші пікір жалған, екінші - жалған, күрделі пікір жалған) ;
1*0=0 (бірінші пікір ақиқат, екінші-жалған, күрделі пікір жалған) ;
1*1=1 (екі пікірде ақиқат және күрделі пікірде ақиқат) .
Техника жүзінде, коньюнкция коньюнктор деп аталатын құрылғысымен іске асырылуы мүмкін. Коньюнктордың қарапайым моделі болып, бірнеше электрлік кілттердің (k1, k2) . Бұл жағдайда қарапайым ақиқат пікірге кілттің тұйықталуы, ал ақиқат күрделі пікірге - Л жанып тұрған электр шамы сәйкес келеді.
Логикалық элемент - коньюнкторды - жартылай өткізгішті диоттарда жүзеге асыруға болады. Ақиқат пікірге үлкен потенциал сәйкес келеді, ал жалған пікірге - кіші потенциал сәйкес келеді. Е нүктесіне потенциал қосылған; егер барлық диодтарға осындай потенциал қосылса (А, В және С нүктелері), онда тізбекте ток болмайды және Д нүктесінің потенциалы Е нүктесіндегідей, яғни үлкен болады. Бұл күрделі пікірдің ақиқат болуына сәйкес келеді. Егер, ең болмағанда бір диотқа аз потенциал қосылса (жалған пікір), онда диод арқылы ток өтеді, ол R резисторы арқылы өтеді. Сөйтіп, Д нүктесінің потенциалы азайып қалады. Бұл күрделі пікірдің жалған болуына сәйкес келеді.
Логикалық функция «НЕМЕСЕ». Дизьюнкция (бөлу) - «НЕМЕСЕ» логикалық функциясы. Егер ең болмағанда оны құрайтын пікірлердің біреуі ақиқат болған жағдайда ақиқат болатын және егер күрделі пікірді құрайтын пікірлердің екеуі де жалған болған жағдайда жалған болатын күрделі пікірді дизьюнкция деп атаймыз. Дизьюнкция «+» таңбаларымен белгіленеді, ол немесе деп оқылады. Екі пікірдің дизьюнкциясы логикалық қосу ережесі болып жазылады:
0+0=0 (екі пікірде жалған, және күрделі пікірде жалған) ;
0+1=1 (бір пікір жалған, екіншісі-ақиқат, күрделі пікір ақиқат) ;
1+0=1 (бір пікір ақиқат, екіншісі-жалған, күрделі пікір ақиқат) ;
1+1=1 (бір пікір ақиқат және күрделі пікірде ақиқат)
Техника жүзінде, дизьюнкция дизьюнктор деп аталатын құрылғымен іске асырылуы мүмкін. Бұл жағдайда ақиқат қарапайым пікірге кілттің тұйықталған күйі, ал күрделі ақиқат пікірге - Л жанып тұрған электр шамы сәйкес келеді. Көрініп тұрғандай, бір тұйық кілт болғанның өзінде де, шам жанып тұрады. Логикалық элемент - дизьюнкторды жартылай өткізгіштік диодтарда іске асыруға болады. А, В және С нүктелердің ең болмағанда біреуіне үлкен потенциал берілсе, онда сәйкестелетін диод арқылы ток өтеді, резисторға кернеу түседі де, Д нүктесінің потенциалы Е нүктесіне қарағанда үлкейеді (нольге қарағанда) . Бұл күрделі пікірдің ақиқат болуына сәйкес келеді. Егер барлық қарапайым пікірлер жалған болса, онда диодта Д нүктесіндегідей аз потенциал болады.
Логикалық элемент, ЕМЕС логикалық функциясын іске асыратын құрылғы инвертор деп аталады.
Қазіргі ЦЕМ-дың логикалық элементтері интегралдық схемаларда жасалады немесе үлкен интегалдық схемаларда. Интегралдық технологияның дамуы жоғарыда көрсетілген схемаларға қарағанда, едәуір күрделі логикалық схемаларды құрастыруға мүмкіндік береді. Логикалық функциялардың кестесінің мәндері.
Логикалық өрнектің нәтижесі ақиқат (True) немесе жалған (False) болады. Логикалық өрнек логикалық тұрақты, логикалық айнымалы, логикалық функциялардан, қатынас және логикалық амалдардан, жақшалардан құралады. Қатынас амалдары (=, < >, <, >, <=, >=) екі арифметикалық өрнектің нәтижелерін салыстырып, ақиқат немесе жалған екендігін анықтайды. Мысалы: 14<11+3- ақиқат, себебі алдымен арифметикалық өрнектер есептелініп, сонан соң нәтиже салыстырылады. Салыстырылатын шамалар файлдық типтен басқа кез келген типте болады.
Логикалық амалдарға қатысты шамалардың типі логикалық болуы қажет. Берілген кестеде Паскальда қолданылатын логикалық амалдар көрсетілген. Амалдардың орындалу басымдылығы: not, and, or. Паскальда логикалық логикалық амалдар қатынас амалдарынан бұрын орындалады. Мысалы, А<10 and B<100 өрнегінде алдымен «10 and B» амалы орындалуы керек, логикалық амал логикалық типті шамалармен орындалатын болғандықтан, бұл жерде қателік туады, сондықтан амалдардың орындалу ретін жақшамен көрсеткен жөн, яғни былай жазған дұрыс: ( A<10) and (B<100) . Математикада жиі кездесетін қос теңсіздікпен берілген өрнекті жақша мен логикалық and амалы көмегімен логикалық өрнек түрінде: мысалы, 1<=x<=50 былайша (1<=x) and (x<=50) түрінде жазылады.
Программалау тілдерінде логикалық өрнектер шартты операторлардың жұмысын ұйымдастыруда пайдаланылады.
Электрондық есептеу машиналары берілген программа бойынша есептеу амалдарын орындауға арналған құрылғы. Қазіргі уақыттағы электрондық есептеуіш машиналар - өзінің жаңа технологиялық жетілгендігімен және әртүрлі физикалық жұмыс жасау принциптерімен таң қалдыратын, құрылғылардың күрделі кешені.
Есептеуіш машиналар ақпараттың берілу тәсілдеріне байланысты екі үлкен топқа бөлінеді: үздіксіз орындайтын есептеуіш машиналар, немесе аналогтық есептеуіш машиналар (АЕМ), және дискретті орындайтын есептеуіш машиналар, немесе цифрлық есептеуіш машиналар (ЦЕМ) . АЕМ-де кіру, шығу және аралық шамалар токтар немесе кернеулер түрінде беріледі, олардың мәндері белгілі бір масштабтағы сандарға сәйкес келеді. АЕМ-де сандармен орындалатын математикалық амалдар, электр токтарының немесе кернеулердің әртүрлі түрленуімен алмастырылады.
1. 1 Логика алгебрасы функцияларын минимизациялау және оны қарастырғандағы шектеулер
Мүлтіксіз дизъюнктивті қалыпты форма (МДҚФ) жазудың тиімді формасы болмайтынын мысалда көрсетейік:
f(Х
1
, Х
2
) = Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
=Х
1
Х
1
Х
2
=Х
1
 Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Сонымен құрылғыны синтездеу есебі ондағы жабдықтарды азайту есебімен толықтырылуы керек. Математикалық көзқарастан бұл есеп минималды ЛАФ-ын құру есебі.
Минималды ЛАФ-ы дегеніміз бастапқы формадағыдан аз әріптер санына тұратын форма.
Егер қандай да бір терімде f а
1
мінін қабылдаса, ал
 а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
 функциясының а
2
мәнін жабады деп айтады.
функциясының а
2
мәнін жабады деп айтады.
ЛАФ-ын минимизацилаған кезде бастапқыға қарағанда аз әрпі бар форманы алуға тырысады.
Дизъюнктивті қалыпты формаға қатысты бұл форманы қысқартылған дизъюнктивті қалыпты форма (Қысқ. ДҚФ) деп атайды. ҚДҚФ құрудың мәні оның құрамына бастапқы функцияның бір емес бірнеше бірлігін жабатын бірліктері бар элементар көбейтулер кіреді.
ҚДҚФ - ға кіретін әрбір элементар көбейтінді функцияның тек бір бірлігін жабады.
ҚДҚФ-ны алу тәртібі төмендегідейболуы мүмкін.
1. Бастапқы МДҚФ-ның бірліктерінің конституенттеріне барлық толық емес жабыстыру операцияларын орындау. (n-1) -рангті көбейтінділер шығады. Қалған жапсырылмаған бірліктің конституенттері келешектегі жабыстыруларға қатыса алмайды.
2. Алынған барлық бірлік конституенттерімен көбейтінділерінің жабуын жүргізу. Кейбір бірлік конституенттерінің бөлігі шектеледі.
3. 1) және 2) операцияларын мүмкін болғанша жүргізу.
Мысал 1
f(Х
1
, Х
2
) = Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
Егер толық жабыстыру операциясын қолдансақ онда:
f(Х
1
, Х
2
) = Х
1
 Х
1
Х
2
Х
1
Х
2
немесе
f(Х
1
, Х
2
) = Х
1
Х
2
 Х
2
Х
2
яғни, операцияны ары қарай жүргізуге мүмкіндік жоқ.
Енді толық емес жапсыру операциясын қолданайық:
f(Х
1
, Х
2
) = Х
1
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
2
= Х
1
Х
2
= Х
1
 Х
2
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
Х 1 , Х 2 - қарапайым импликанттар
Х 1 Х 2 , Х 1 Х 2 , Х 1 Х 2 - бірліктің коституенттері
Енді жою операциясын жүргізе аламыз:
Х 1 Х 1 -ді жояды, Х 1 Х 2 , Х 1 Х 2
Х 2 Х 2 - ні жояды, Х 1 Х 2 , Х 1 Х 2
Яғни Қысқ. ДҚФ
f(Х
1
, Х
2
) = Х
1
 Х
2
біздің жағдайымызда бұл минималды форма
Х
2
біздің жағдайымызда бұл минималды форма
2 АЛФ-ны Квайна-Мак-Класки әдісімен минимизациялау
Жалпы жағдайда құрылғы n кірістен және m шығыстан тұруы мүмкін. m=1 жағдайында біршығысты схема орын алады, қарсы жағдайда көп шығысты схема қалыптасады.
Құрылғы кірісіне {Х}кіріс алфавитінен тұратын кіріс сөздері келіп түседі, ал шығыста {У}шығыс алфавитінен тұратын шығыс сөздері болады. n кіріс және m шығыс кезінде, кіріс сөзі n шамасын құраса, шығыс сөзі m шамасын құрайды.
Егер құрылғы жұмысы t i моментте толығымен t i уақыт мезетінде келіп түскен кіріс сөзбен анықталатын болса, онда мұндай құрылғыны комбинациялық схема немесе жады құрылғысы жоқ ақырғы автомат деп атайды. Жадысы жоқ ақырғы автомат қарапайым логикалық құрылғы болып табылады, және олардың жұмысы бульдік өрнектермен баяндалады.
Комбинациялық схемаларды жобалау кезінде оларды синтездеу және анализдеу есептерін қарастыруға тура келеді. Комбинациялық схемаларды синтездеу этаптары:
- физикалық баяндамасы бойынша математикалық баяндамасы жасалынады (бульдік теңдеулер жүйесі) ;
- математикалық баяндалуы бойынша алдын ала минимизация есептерін шеше отырып, логикалық схеманы құрайды;
- логикалық схема бойынша функционалдық схема құрайды.
Комбинациялық схемаларды анализдеу барысында синтездеу процесіне қарама қарсы есептер орындалады, яғни қолда бар комбинациялық схема бойынша оның математикалық моделін жасау керек. Сонымен комбинациялық схемаларды синтездеу мәселесін шеше отырып, бульдік функцияларды шешу мәселесі де шешіледі. Бульдік функцияларды іске асырудың негізі болып логикалық элементтер саналады. Екі тұрақты күйі бар элементтер логикалық элементтер ( немесе ауыспалы элементтер ) деп аталады, «0» - ауыспалы элементтің (триггердің, реленің, магниттік жүрекшенің) бір күйі, «1» - екінші күйі. Бульдік айнымалылар және функциялар логикалық элементтердің кіріс және шығыс сигналдарының мәнін бейнелейді.
Бульдік өрнектерге сәйкес біріккен олар логикалық ауыспалы схемаларды құрайды. Минимальді бульдік өрнектер кезінде минимальді комбинациялық схемалар алынады. Минимальді комбинациялық схема жоғары сенімділікпен, минимальді бағамен, жоғары жылдамдықпен сипатталады. Сондықтан комбинациялық схемаларды синтездеу мәселесін шешу барысында алгебра логика функцияларын минимизациялау мәселесін назар аудару керек. АЛФ минимизациялаудың бірнеше әдістері бар: Квайна Мак-Класки, Вейча - Карно және т. б. бірақ бұл аталған әдістер негізінде элементарлы және көршілес конъюнкцияларды жабыстыру және жұту әдістерін қолданып, бастапқы ДЖҚФ функциясы бойынша оның минимальді ДМҚФ алу болып табылады.
х 1 α1 х 2 α2 . . . х n αn конъюнкциясы элементарлы болып саналады, егер ондағы әрбір айнымалы бір реттен артық кездеспейді, мұнда
 i
, егер α
i
=0
i
, егер α
i
=0
x i αi =
x i , егер α i =1
Конъюнкцияны қалыптастыратын әріптер саны (r) ранг деп аталады. Бірдей рангілі екі элементарлы конъюнкция көршілес деп аталады, егер олар бір аргументтің функциялары болып саналса және аргументтердің біреуі тек терістеу (инверсия) таңбасымен ғана өзгешеленсе.
r рангілі көршілес конъюнкциялардың дизъюнкциясын бастапқы конъюнкцияның ортақ бөлігі болып табылатын элементарлы r-1 рангті конъюнкциямен алмастыруға болады (жабыстыру ережесі) . Мысалы, У=х 1 х 2
∨х 1 х 2 x 3 =х 1 x 2 .
2. 1 АЛФ-ны Вейча-Карно диаграммасын қолдана отырып минимизациялау
Вейча-Карно диаграммасын қолданатын минимизациялау әдісі көрнекі және қарапайым минимизациялау түрі болып табылады. Және бұл жағдайда АЛФ бейнелеудің графикалық әдісі қолданылады.
Вейча-Карно диаграммасы 2 n квадратты тікбұрышты бейнелейді, мұндағы n - графикалық түрде бейнелеуге қажетті бульдік функцияның айнымалылар саны. n - жұп кезінде, тікбұрыштың әрбір жағы ұяшықтан тұрады, ал n - тақ кезінде тікбұрыштың бір жағы
ұяшықтан, ал басқа жағы
ұяшықтан тұратды. n аргументке тәуелді АЛФ-ң кез келген екі диаграммасы n+1- аргументке тәуелді АЛФ диаграммасын қолданады. Диаграммадағы әрбір ұяшыққа сәйкес элементарлы конъюнкция (аргументтер жиынтығы) қойылады, және де бұл жағдайда көршілес конъюнкциялар сәйкес келеді. Екі шеткі қарама қарсы қатарлар мен бағаналардағы ұяшықтар да көршілес конъюнкциялар болып саналады (диаграмма тода орналасқан деп елестетуге болады) .
Диаграмманың әрбір ұяшығындасәйкес жиындағы АЛФ мәніне байланысты «0» немесе «1» мәндері қойылады. Жабыстыру және жұту графикалық түрде (визуальді) орындалады.
Мысал 1. 2. У= х 1 х 2
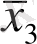
V х 1
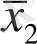
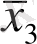
V х 1 х 2 х 3 х 4 V
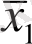
х 3 х 4 + х 1
х 3 х 4 V
1 x 2 x 3 x 4 функциясын минимизациялау.
Шешімі. n=4 болғандықтан берілген функцияны минимизациялау үшін оналтылық квадраттық диаграмма саламыз. Бастапқы формула мүшелеріне сәйкес квадраттарды бірмен белгілейміз.
Жауабы:
У
min
=x
3
x
4
Vx
1
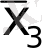
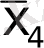 .
.
2. 3 Карно картасы және Вейч диаграммасы
Егер логикалық айнымалылардың саны 5-6 айнымалыдан аспайтын болса, логикалық теңдеулердің түрлендірулерін Карно картасы немесе Вейч диаграммасы арқылы жасауға болады. Түрлендірудің мақсаты - ықшамдалған логикалық теңдеу алу (минимизация) . Минимизді-Карно картасында жиындарды біріктіру үшін шығарады. Біріктірілген жиындар функцияның бірдей мәндерін қабылдауы керек (барлығы 0 немесе барлығы 1) .
Көз жеткізу үшін мысал қарастырайық: келесі ақиқат кестесінде көрсетілген 3 айнымалы X, Y, Z, fm можоритарлы функцияға арналған логикалық теңдеуді табу керек болсын:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz