Математикалық логиканың элементтері

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

Кіріспе

Мектептегі математика өз тарихында талай өзгеріске түсіп, толықтырылып, қайта өзгеріске ұшырап отырды. Математикалық білімнің дәйекті мәселелері іріктеліп, енгізгі бағдар ретінде жинақталып, жүйеленіп, басқа ілімдердің табыстарымен қабыстырыла, мектеп оқулықтарына енгізіледі. Ол үшін дидактикалық өңдеуден өткізіліп, тәжірибелер жасалып, түзетіліп, қайта баяндалады.

Материалды іріктеуде қоғам талаптары, оның дамуы ескеріледі. Дәстүрлі білім жүйесі мен қазіргі білім жүйесін қарастырайық. Математикалық білімнің жаңа көзқарастарын мұғалім өзі түсініп, оны оқушыға жеткізуі оңай іс емес. Оған қыруар күш, мемлекеттік қомқорлық.

1908 жылы Римде ІV халықаралық конгресте математикалық білімді жаңалау үшін халықаралық сарапшылар тобы құрылды. Олар дәстүрлі математиканы оқыту мәселесіне арналған 250 кітап жазды. Әрбір елге арнап, жаңа бағдарлама құрастырды. Сол бағдарламаға сай оқулықтарды, оқыту әдістемесін құрастырды.

Алайда, жиырмасыншы ғасырдың екінші жартысында математика ел қуатын, экономикасын анықтаушыға айналды. Осыдан да 1950 жылы математикалық білімді жаңалаушы интернационалдық алқа, ал 1958 жылы ғылымдар бірлестігінің Ғылыми тобы құрылды. 1959 жылы ол топтан мектепте математиканы оқытудың жаңа көзқарасын зерттеу бөлімі бөлініп шықты. Олар алдына екі мақсат қойды:

Математика ғылымы мен математика пәнінің арасын жақындастыру;
Міндетті түрде барлық оқушының шығармашылық бастамасын ояту және ерікті түрде математиканың бір бағдарын таңдауға мүмкіндік беру.

Математикалық білімнің халықаралық алқасы өз жұмыстарының нәтижелерін 1958 жылы Эдинбургте, Стокгольмде, Мәскеуде өткен математикалық халықаралық конгрестерінде қарап, 1965 жылы Парижде шыққан “Орталау деңгейде математиканы оқытудың жаңа көзқарастары” деген басылымда және мемлекеттік басылымдарда жарияланды.

Оларды талдап, сынға салудың қорытындысында:

жиындар теориясының түзгіштерін;
математикалық логикаға кіріспені;
қазіргі алгебра ұғымдарын;
ықтималдықтар теориясы мен статистикаға кіріспені мектеп бағдарламасына енгізуіне ұсынады.

Осыны бағдарға алып, бұрынғы Кеңес елінде 60-жылдардың ортасында эксперименттер жүргізіліп, математика бағдарламалары құрастырылып, оқулықтар жазылды. Бүкіл алгебра, геометрия математикадан қосымша әдебиеттер осы негізде жасалды. Мектеп мұғалімдері қайта даярлықтан өткізіліп, математиканы оқыту әдістемелері жаңадан жазылды. Сондай- ақ, жоғары мектеп бағдарламалары өзгертіліп, алуан түрлі оқу жүйесі пайда болды.

Бұл шаралар ойдағыдай нәтиже бермеді. Жиындар теориясы мен математикалық логика түзгіштері негізінде жаңаланған білім оқушыға да, мұғалімге де ауыр болып, көздеген мақсаттан шықпады.

Векторлар мен координаталар жүйесі мектеп оқу құралдарынан орын алды. Оларды оқытудың әдістемелік жүйесі әлі де жетілдіріліп, оқыту мазмұны нақтылана түсетіні айқын.

Бұрынғы Кеңес өкіметі тарап, еліміз егемендік алған кезде, нарыққа көшу саясатында математикалық білімнің мазмұнына жаңа талаптар қойылғаны хақ. 1991 жылы Қазақстан Республикасы Білім министрлігі жанынан құрылған алқа өз жұмысын бастады.

Алдағы уақытта бұл оқулықтр өмірдің ағымына сай толықтырылып, сарапталып барша оқушы қауымға жеткізілетіндігіне күмән жоқ.

“Математика” деген атауыштық есім ежелгі гректер тіліндегі “mathema” (білу, білік, ілім) және “tehnica” (өнер, ісмерлік, шеберлік) деген мағынадағы әртүрлі екі сөздің қиюласуынан жасалған күрделі құрылымға жатады. Бұл құрамды сөз, әу баста, “білу өнері” яки “біліми өнер” деген мағынада қолданыс тапқан. Оқыту мен ғылым дүниесінде “математика” сөзін осы айтылмыш мағынасында алғаш тұтынған адам - ол ежелгі грек жұртының әлемге аян данагері әрі өнерпазы Пифагор (б. з. б. 580-500 жж. ) болған.

Пифагор және оның ізбасарлары мен шәкірттері - “пифагорейшілдер” өздерінің дүние танымдық ұраны етіп, “Бәрі - сан” деген қалыптамалық қағиданы ұстанғаны тарихқа танымал шындық. Бұл қалаптаманы тарқата талдасақ, одан фифагордың: “дүниедегі бәр нәрсе саннан жасалған және тек саннан тұрады” - деп пайымдағанын көруге болады. Сондықтан да, Пифагорды - сандар математикасының атасы деп атаған.

Пифагор заманында сан деп, негізінен, 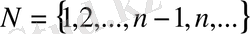натурал сандар жиыны ұғылған. Пифагордың өз анықтауы бойынша: “Сан дегеніміз тақтар мен жұптардың жиналымы”. Пифагор “бірлікті” сан ғана емес “санды жасаушы” деп атаған. Оның тұжырымы бойынша әрбір сан бірліктер жиынтығынан (қосындысынан) тұрады.

Мысалы: 3=1+1+1; 8=1+1+1+1+1+1+1+1.

Қазіргі замандық яғни 20 - ғасырдағы білімтану жүйесінде математика былайша анықталады:

1 - анықтама. Қазіргі заманғы аксиоматикалық қалыптама тұрғысынан алып қарағанда математика деп абстракциялық форма - математикалық структуралар жиналмасын ұғады. (Н. Бурбаки)

Мұндағы “структура” (қазаша: құрылым) деген ұғыми сөздің мағынасы “операция” (амал) және “қатынас” деген ұғымдар арқылы анықталып көрсетіледі.

2 - анықтама. Егер қандай да бір А жиынында Т деген амал және Р қатынас енгізілсе, онда А жиынын структура (құрылым) деп атайды.

Егер А жиынында Т математикалық амал және Р математикалық қатынас берілсе, онда А жиынында Р - математикалық структура анықталған дейміз. Ал А жиынында Т логикалық амал мен Р логикалық қатынас енгізілген болса, онда А жиынында логикалық құрылым жасалған деп айтуға болады. Осы үлгімен “грамматикалық структура”, “биологиялық структура” т. с. с. деген ұғыми тіркестер жасалған.

А жиынында Т амал мен Р қатынас арқылы анықталған S - математикалық құрылымды (структураны) қысқаша былай белгілеп жазады:

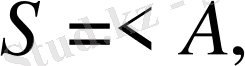
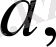
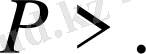
Мұнда: 1) А - базалық (тұғырлық) жиын; 2) а - жекеленген элемент; 3) Т - операция; 4) Р - қатынас.

Бүгінгі белгілемелік, қалыптамалық тілде Пифагордың сандық математикасы мынадай сандық құрылым деп қарауға болады:

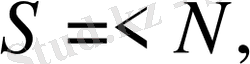
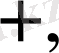
Мұнда: 1) - құрылымның тұғырлық жиыны; 2) 1 - бірлік сан, құрылымның жекеленген элементі; 3) - математикалық амалдар; 4) - математикалық қатынастар.

Сөйтіп, байырғы сөйлеу тілімізде Пифагордың сандық математикасын былайша анықтауға болатынын көреміз:

Пифагордың сандық математикасы деп - оң таңбалы бүтін сндар жиынындағы бірлік элемент жекеленген және сол жиынның элементтері үшін “қосу”, “алу”, “көбейту”, “бөлу” амалдарымен қатар “тең”, “кіші”, “үлкен” қатынастары анықталған 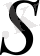- математикалық құрылымды айтады.

Қазіргі біліми тілде “операция” (амал) сөзі әр алуан түрлендіргіш әрекетті яки қызметті белгілейді. Математикалық амал “бейнелеу” деп аталатын танымдық ұғым арқылы анықталады.

Мысалы. 3+4=7 теңдігін алайық. Бұл өрнекті қазіргі заман математиктері: “Қосу амалы (3, 4) қосын 7 санына бейнелейді” - деп қарастырады. Бұл сөйлемді белгілемелер тілінде мынадай қалыптама арқылы жазып көрсетуге болады:

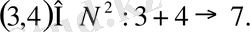
Жалпы танымдық тілде: (3, 4) қосты бейнелеудің түпнұсқасы, ал 7 санын оның бейнесі немесе бейнелік көшірмесі деп атайды.

Математикалық білім атаулының түбегейлік мақсаты ақиқаттығы бұрыннан тағайындалған белгілі бір ойқорытындыларына сүйене отырып, қандай да бір жаңа ойқортымның ақиқаттығын (растығын, дұрыстығын) дәлелдеу боп табылады. Сондықтан да, ғылым танымгерлері дәлелдеу амалын математиканың жүрегі немесе жаны деп атайды. Математикалық ойқорытуларда дәлелдеу амалының қажеттігі мен мүмкіндігін алғаш атап көрсетуші адам - ол ежелгі гректерден шыққан әйгілі жеті данагердің көш басшысы Фалес (б. з. б. 625-548) болған. Фалестің дәлелдеу туралы ойын сандар математикасында тұңғыш рет Пифагор қолданған.

Математикалық дәлелдеу жайында Фалес пен Пифагор алғаш бастап салған жолды тиімді жалғастырып, оны, шын мәнінде, ғылыми шыңына алғаш жеткізуші ежелгі грек математигі Евклид (б. з. б. 356-300) болғанын тарихтан білеміз. Ғылым тарихында Евклид, заңды түрде, ғылыми математиканың атасы деп аталады.

Қазіргі замандық математиканы “құрылымдар математикасы” деп анықтаушы Никола Бурбаки болғанын жоғарыда айттық (Н. Бурбаки 20 - ғасырдағы Францияның бір топ талантты математиктерінен құрылған жасырын ұжымның бүркеншек аты) .

Бурбакишілдер: “Ежелгі гректер заманынан бері қарай “математика” деп айту “дәлелдеу” деген сөзбен пара-пар айтылады” -деп көрсетеді.

Алдыңғы айтылып өткен: “бейнелеу”, “амал”, “әрекет”, “дәлелдеу” - деген танымдық сөздердің баршасы білім әлеміне логика пәні арқылы келіп енген атауыш сөздер қатарына жатады. Сонымен қатар олардың мазмұны мен танымдық мағыналары тек логика пәні ауқымында ғана толық әрі айқын ашып көрсетіледі. Сондықтан, ендігі сөз логика туралы болмақ.

“Логика” сөзі, әу баста, ежелгі гректер тіліндегі “logos” (сөз, ой, сана) деген сөзінен шығып қалыптасқан. Білім тарихын зерттеушілер “логика” сөзін ғылымға алғаш енгізген адам - ол ежелгі грек білімпазы Демокрит (б. з. б. 460-370) болған деп көрсетеді. Демокрит “Ойлау ережелері” деген ғылыми еңбек жазған. Осы тарихи шығарманың айдарлық тақырыбына “логика” пәнінің аты келіп шыққан.

Логика басында дүниетану мәселелерін зерттейтін жалпы философиялық білімнің бір саласы ретінде дүниеге келеді. Ол дара пән боп б. з. б. ІV ғасырда қалыптасқан. Өздік зерттегіш әдісі және зерттеу нәрсесі бар логика атты дара пәннің негізін алғаш рет әлемнің бірінші ұстазы атанған әйгілі білімпаз, ежелгі грек данагері Аристотель (б. з. б. 384-322) қалаған. Ғылыми білімнің тарихшылары мен танымгерлері Аристотель логикасын ақиқатты ашу және негіздеу қаруы (органон) немесе “дәлелдеу туралы ғылым” деп атайды.

Орта ғасырлық Қазақстандағы байырғы шаһарлардың бірі Отырар (арабша аты Фараб) қаласының төл тумасы, әлемнің екінші ұстазы (Аристотельден кейінгі ұстаз) атанған Абу - Насыр әл - Фараби (870-950) Аристотель логикасын терең талдау, кемелдендіре кеңейту және жалпақ жаһанға жарлап тарату жұмыстарымен ұзақ жылдар бойы айналысады. Ол өзінің философияны оқып үйренуге қажетті білімдер тізімін анықтайтын еңбегінде тілтану оқуын бірінші, ал логиканы екінші орынға қойып қарастырады.

Екінші ұстаз тағы бір шығармасында логиканы сөздер грамматикасымен салыстыра қарайды. “Грамматика - деп пайымдайды ол, - адамдардың сөйлеу тілін қалай туралайтынын қарастыратын болса, логика ғылыми қателер жіберу қатері туған тұста адам ойының дұрыс болуын солай туралап отырады”.

Алдыңғы айтылғандардан, логиканы ақиқатқа жету үшін қалай дұрыс ойлай білу керек екендігін зерттейтін ғылым деп қарауға болатынын көреміз. Логика пәнінің нақты мақсаты мен мазмұнын айқын ашып түсіндіру үшін, әуелі, “ойлау”, “ақиқат ой”, “дұрыс ой” деген ұғымдардың мазмұнын айқындап алған абзал.

Ойлау адам арқылы мен санасының әрекеттік қызметіне жатады. Адамның ойлау органы - ми. Оның ойлау қызметі туралы ұғым “бейнелеу” және “тану” деп аталарын түптектік ұғымдар арқылы анықталады.

3 - анықтама. Айналадағы нәрселер мен құбылыстардың адам санасындағы бейнеленуін тану деп атайды. Танудың нәтижесін таным немесе білім дейді. Тану әрекеті іске асырылу сипатына қарай екі түрлі деңгейге жіктеліп қарастырылады: 1) сезім деңгейіндегі тану; 2) ақыл-ой , ой- сана деңгейіндегі немесе рационалдық деңгейдегі тану.

Сезім арқылы тану қызметі түйсіну, қабылдау және елестету - деп аталатын амалдар жүйесі арқылы іске асырылады. Бұларды тікелей тану немесе алшақтамай тану жолдары деп те атайды. Тікелей (аулақтамай) танудың өздік логикасы бар, оны сезу логикасы деп атайды. Бұл логиканың ауқымында: “қуаныш”, “реніш”, “үміттеніс”, “түңіліс” т. с. с. ұғымдар қарастырылады.

Ақыл-ой яғни саналы (рационалды) түсінім деңгейіндегі тану қызметі ойлау, пайымдау, ұғыну әрекеттері арқылы атқарылады. Бұларды, көбінесе, тікелей емес тану немесе аулақтатып тану деп те атайды.

4 - анықтама. Ойлау деп шынайы өмірдегі нәрселер мен құбылыстардың сөз арқылы адам санасындағы түрлендірілуін айтады.

Сөйтіп, ойлау дегеніміз ақыл - ойдың тануы яғни бейнелеу немесе түрлендіру әрекеттері арқылы іске асырылатын ми қызметі екенін көреміз. Айналамыздағы танылатын нәрселер мен құбылыстарды бір сөзбен айтқанда, затиялық нәрселер немесе заттық нәрселер деп қарауға болады. Ал затиялық нәрселердің адам санасындағы көшірмесін (кескінін, суретін, бейнесін) санауялық нәрселер (идеялар, ойлар) деп атайтын боламыз.

Ақыл-ойға ұялаған санауялық бейненің затиялық формасы (қалыбы) сөз болып табылады. Сөз - ойдың сыртқы қабы немесе қалыбы (формасы) болып есептеледі.

Сөйтіп, ойлау амалының қалыбы мен қаруы сөйлеу тілінің сөздері боп саналатынын көреміз. Сөз адам санасындағы нышандық белгілемесі (символикасы), қалыптамасы (формасы) және ойды туғызушы, жасаушы боп қызмет атқарады. “Сөз сөзден туады сөйлемесе қайдан туады” деген халық даналығы сөздің осындай ой тудыратын, ой сақтайтын және ойды жеткізетін құдыретті қасиетімен байланысты айтылған деуімізге болады.

Алдыңғы айтылғандарды тілге тиек, ойға арқау ете отырып, логика пәнін осылайша анықтауға болады.

5 - анықтама. Логика - ақиқат және дұрыс ойлаудың формасы (қалыбы), заңдары мен ережелері туралы ілім.

Ойлаудың формасы (қалыбы) деп шынайы өмірдегі нәрселердің қасиеттері мен қатынастарын бейнелеу әдістерін атайды. Логика пәнінде, негізінен, үш түрлі ойлау қалыбы қарастырылады. Олар: 1) “ұғым”; 2) “пайым” және 3) “ойқорыту” деп аталады. Ойлау формаларының әрқайсысына белгілі бір тұлғалық құрылым тән болып келеді. Бұл құрылымдарды өрнектеп көрсету үшін арнаулы белгілемелер (символикалар) жүйесі қолданылады. Осындай белгілемелер тілінде өрнектелген ойды формальданған (қалыптанған) ой деп атайды. Ой біткеннің нақтылы мазмұны және айқын құрылымы болады. Ой мазмұнын сол ой бейнелейтін нәрселердің қасиеттері мен қатынастары жасайды. Ойдың қалыбы (формасы) немесе құрылымы (структурасы) боп ой бөлшектерін құрмаластыру жолдары саналады. Ой мазмұнына қарай ақиқат және жалған болып екіге бөлінеді.

6 - анықтама. Шынайы өмір нәрсесі мен құбылысының адам санасында дәлме-дәл және бекім бейнеленуін ақиқат ой деп атайды. Ақиқат ойға қарама - қарсы мазмұндағы бейнелеуді жалған ой деген сөз арқылы атап көрсетеді.

Сөйтіп, “ақиқат-ой” немесе қысқаша “ақиқат” деп мазмұны шынайы шындықты дәлме - дәл бейнелейтін ой ғана айтылатын көреміз. Егер ой мазмұны жағынан шынайы шындыққа сәйкеспейтін болса, яғни шындықты бұрмалайтын болса, ондай ойды “жалған ой” қатарына жатқызуға болады.

Формасы (қалыбы) немесе структурасы (құрылымы) жағынан алғанда ой дұрыс (тура) ой және дұрыс емес (қате) ой боп екі жікке бөлінеді.

Ойдың ақиқаттығы мен дұрыстығы әрқашан бір-бірімен етене байланыста боп келеді.

Тану барысында анық ақиқатқа жету үшін мынадай екі шарттың мүлтіксіз орындалуы ләзім: 1) ойлауға арқау болатын түптұғырлық, бастамалық ойлар ақиқат болуы шарт; 2) ой құрылымы жағынан дұрыс болуы тиіс.

Ойдың ақиқат әрі дұрыс болуын ұйымдастыратын және қадағалайтын біліми пән логика деп аталады.

Математикалық логиканы, екінші сөзбен, символикалық (белгілемелік) логика деп атайды. Кейде бұл атаулармен қатар “теориялық логика” деген атауыш сөздер тіркесі де қолданылады. Ойлау қызметінің формаларын, заңдарын және әдістерін зерттейтін ғылымды білімтану жүйесінде формальдық логика (Аристотель логикасы, дәстүрлік логика немесе жалпы логика) деп атайтынын білеміз. Логика пәнінің даму трихында ойлау заңдары мен ережелерін баяндау үшін символикалық тілді алғаш бастап қолданушы адам Аристотель болғаны жоғарыда айтылды. Сондықтан дәстүрлік логиканы белгілемелік яғни математикалық логиканың бұлақтық бастауы немесе түптегі деп қарауға әбден болады. Алайда, Аристотель логикасының басты баяндау тілі адамның байырғы сөйлеу тіліндегі сөздер жүйесі боп келеді. Табиғи тілдің сөздері қашанда көп мағыналы белгілемелік құрал болғандықтан, олар сөйлеу нәрселерін адам санасында дәлме-дәл бейнелей алмайды. Сондықтан дәстүрлік логиканың баяндау тілін математикаланған белгілемелік тілмен немесе формальданған жасанды тілмен жабдықтау қажеттігі кеп туған. Ғылым атаулыны әмбебап (универсал) белгілемелік тіл арқылы баяндау идеясын алғаш ұсынған адам ол немістің ұлы математигі әрі философы Г. В. Леибниц (1646-1716) болған. Соның бағдарламалық пайымдамасы бойынша бір ғылымды әркімге ұғынықты ортақ әмбебап тілмен баяндау үшін, алдымен, “адамзат ойының әліпбиі” жасалуы тиіс. Ондай әмбебап әліпби екілік санау жүйесі негізделген математикалық тілден тұруы керек. Г. В. Леибництің осы бағдарламалық ойына қарап, оны қазіргі замандық математикалық логика пәні мен кибернетикалық техниканың теориясын ашуға алғаш жол нұсқаған данышпан деп санайды.

Логикалық ой - құрылымын математикалық есептемелер арқылы өрнектеу және оны түрлендіру жолын іс жүзінде алғаш жасаған адам, ол ағылшынның кемеңгер математигі әрі логигі Джордж Буль (1815-1864) болған. Ол өзінің “Логиканың математикалық талдамасы” (1847 ж. ) және “Ойлау заңдарын зерттеу” (1854 ж. ) деп аталатын ғылыми еңбектерінде логикалық қалыптамалар мен құрылымдарды баяндауға өз заманындағы алгебралық әдістерді кеңінен пайдаланады. Соның нәтижесінде қазіргі кезде “Буль алгебрасы” деп аталып жүрген жаңа пәннің негізі қаланады. Математикалық логиканың баяндау тілі ретінде жасалған “Буль алгебрасы” қазіргі замандық электронды есептегіш машиналардың (ЭЕМ-дың) логикалық және есептегіш тетіктерін жасауда және олардың қызметін модельдеуде кеңінен қолданылады.

Сөйтіп, Аристотельдің дәстүрлік логикасы Буль алгебрасының арқасында математикалаған символикалық логика қалпына келтіріледі. Осы ахуал формальдық логика теориясының құрылымы мен қызметін тереңдеп зерттеуге математикалық әдістерді кеңінен қолдануға төте және даңғыл жол ашты. Соның нәтижесінде дәстүрлік логика табиғи тілмен қатар жалпы формальдық тіл атаулыны зерттейтін металогика деп аталатын жаңа білім саласының өмірге келуіне себеп болды. Мұндағы “meta” - грек сөзі, қазақша: “кейінгі”, “келесі” деген мағыналы сөздерге сәйкес келеді. Сондықтан “металогика” сөзі “логикадан кейінгі пән” яғни “логиканы зерттейтін келесі пән” деген мағынаны білдіреді.

Осылайша мазмұндық ауқымы барынша кеңейтіліп, әдістемелік қаруы кемелденген логика білімі 19 - ғасырдың аяқ шенінде математиканың негіздемелік мәселелерін тереңдеп зерттеуге батыл да байыпты жұмсала бастайды. Айтылмыш бағыттағы ғылыми зерттеулер саласында айтарлықтай табысты еңбек етіп, логикалы - математикалық білімге үлкен үлес қосқан кемеңгер математиктер мен логиктердің кейбіреуін атап білген абзал. Математиканы логикаландыру бағытында алғаш бастап өнімді де өрелі еңбек етуші ғалымдардың бірі - немістің математигі әрі логигі Г. Фреге (1848-1925) болған. Ол математика атаулыны логика тілі арқылы негіздеуге батыл талпыныс жасайды. Ғылым танымгерлері Г. Фрегенің 1870 жылы жарық көрген “Ұғымдар есептемесі” атты еңбегін математиканы логикаландырудың немесе математиканы формальдандырудың бастамасы болады деп санайды. Бұл игі бастаманы іле жалғастырып дамытушылар: Италияның әйгілі математигі Дж. Пеано (1858-1932), ағылшын математигі әрі философы Б. Рассель (1872-1970) және немістің кемеңгер математигі Д. Гильберт (1862-1943) болды. Осы аталып өткен танымал математиктер мен талантты логиктердің табанды да табысты еңбектерінің арқасында Метаматематика (математикадан кейінгі пән немесе математиканы зерттейтін келесі пән) деп аталатын ғылымтанымдық жаңа пән жасалды.

Метаматематика ілімі математиканың негіздемелік және дәлелдемелік мәселелерін формальданған логиканың әдістерімен зерттейтін математикалық логика пәнінің жаңа бір саласы болып табылады.

Алдыңғы айтылғандардың бәрін салыстыра сараптай айтар болсақ, “математикалық логика дегеніміз не?” деген сауалға сай келетінін жасуапты бір сөзбен мынадай қалыптама түрінде беруге болатын секілді:

Математикалық логика = математикаланған логика + логикаланған математика.

Бұл дипломдық жұмыстың мақсаты: мектеп қабырғасында және де жоғары білім беру ордаларында оқытылатын математикалық логика элементтері пәнінің кейбір тұстарын нақтылап, мысалдар келтіру арқылы айқындап көрсету.

І. Математикалық логиканың элементтері

1. 1. Сөйлемдер мен пікірлер

Қоршаған ортаны танып білу барысында адамдар объектілердің арасындағы, объектілер мен олардың қасиеттерінің арасындағы өзара байланысты анықтайды. Осы байланыс түрлі ұғымдардан құралған сөйлемдер арқылы беріледі. Мысалы, “Тең қабырғалы үшбұрыштың барлық бұрыштары тең”, “28 саны 7 - ге бөлінеді”, “16 жұп сан”.

Әрбір математикалық сөйлем өзінің мағынасымен және логикалық құрылымымен сипатталады. Сондықтан біз сөйлемнің құрылымына ерекше көңіл бөлеміз. Математикада сөйлемдер жәй (элементар) және құрама (күрделі) болып бөлінеді. “28 саны 7 - ге бөлінеді” деген сөйлем жәй. “28 саны жұп және 7 - ге бөлінеді ”, “ 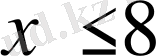”, “Егер үшбұрыш теңбүйірлі болса, онда оның табанындағы бұрыштары тең” сөйлемдері құрама сөйлемдер.

Құрама сөйлемдер жәй сөйлемдер “және”, “немесе”, “егер”, “онда”, “емес” деген сөздермен байланыстыру арқылы жасалады. Бұл сөздер математикада логикалық жалғаулар деп аталады.

Құрама сөйлемнің логикалық құрылымын анықтау үшін

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.