Кванттық механикадағы операторлар теориясы: сызықтық операторлар, меншікті мәндер, өлшеу шарттары және уақыт бойынша эволюция


Кіріспе
І-бөлім. Операторлар жайлы теория
1. Операторлар теориясынан мағұлматтар
2. Динамикалық айнымалыларды /физикалық шамаларды/ сызықтық операторлар түрінде өрнектеу.
2. 1. Координаттар операторы
- Импульс операторы
- Гамильтон операторы
- Толық энергия операторы
- Импульс моменті операторы
3. Бір мезгілде әртүрлі динамикалық айнымалыларды өлшеу шарттары
4. Динамикалық айнымалылардың орташа мәндерінің уақыт бойынша өзгерісі және сақталу заңдары
ІІ-бөлім. Есеп шығару үлгілері
Қорытынды
Пайдаланған әдебиеттер тізімі
Кіріспе
Кванттық механиканың математикалық аппаратында операторлардың алатын орны зор. Классикалық механикада әрбір физикалық шамалар кеңістіктің әрбір нүктесінде кез-келген уақыт мезетінде өзінің сандық мәнімен сипатталады. Мысалы, материалдық нүктенің жылдамдығы кез-келген уақыт мезетінде жылдамдық векторының координат осьтеріне түсірілген проекциялары υ х, υ у, υ ғ шамаларымен анықталады. Басқаша айтқанда классикалық механикада физикалық шамалар уақыт пен координаттың функциясымен анықталады.
Осы курстық жұмыста біз көптеген операторлардың түрімен және уақыттан тәуелділігімен танысатын боламыз. Операторлардың есеп шығаруда алатын орны ерекше болғандықтан, оны ықтималдық тұрғысынан көбірек қолданады.
Біз осы жұмыста операторлардың көмегімен көптеген амалдарды орындап, есеп шығаруда қолданатын боламыз.
Кванттық механикада физикалық шамалар жалпы айтқанда белгілі бір сандық мәндерімен сипатталмайды. Мысалы, бөлшектің орнын анықтайтын шаманы қарастырайық. Классикалық механикада материалдық нүктенің орны әрбір уақыт мезетінде үш санмен нүктенің координаттарымен анықталады. Классикалық механиканың негізгі мақсаты нүктенің осы координаттарының уақытқа тәуелділігінің функциясын табу.
Мақсаты: Операторлар көмегімен есептерді шығарып дәлелдеу.
Жұмыстың өзектілігі: операторларды әртүрлі механика саласында формула арқылы өрнектеу.
І-бөлім. Операторлар жайлы теория
1. Операторлар теориясынан мағұлматтар
Жалпы алғанда, функция дегеніміз бір санға немесе сандар жиынына сәйкес алынатын санды немесе сандар жиынын анықтайтын ереже. Классикалық механикада әртүрлі шамалардың арасындағы функционалдық байланыстарды анықтаумен шектеледі.
Кванттық механикада бұл басқаша. Кванттық механикада нүкте координаттарының сан мәндерінің болу ықтималдықтарын анықтауға және олардың орташа мәндерін есептеуге ғана мүмкіндік болады. Мысалы, егер біз өте көп бірдей, бір-біріне тәуелсіз физикалық жүйелерді алып, олардың барлығы бірдей толқындық функциямен сипатталады десек, онда кез-келген бір физикалық шаманың сандық мәнін өлшеген сайын әртүрлі мәндер аламыз. Кванттық механикада осы физикалық шаманың белгілі бір мәнін алудың ықтималдығы ғана қарастырылады.
Осыған байланысты кванттық механикада физикалық шамалар сан мәндерімен сипатталмай, осы шамалардың операторларымен сипатталады. Қарастырылып отырған мысалда физикалық шамалардың сан мәндері белгісіз болса да, сол физикалық шамалардың операторлары белгілі болу керек.
Функция бір санды басқа бір санмен байланыстыратын болса, оператор бір функцияны басқа бір функциямен байланыстырады. Оператор деп көптеген функциялардың әрқайсысына, осы функциялардан немесе басқа функциялардан сәйкес функция табу ережесін айтады. Операторларды символды түрде әріптердің үстіне мынадай «^» белгі қойып жазады. Мысалы, L ^ , M ^ т. с. с. Егер L ^ операторы u функциясына сәйкес υ функциясын анықтайтын ереже болсаоны символды түрде былай жазады
υ=L ^ u
мысалы, егер L ^ операторы фифференциалдау ережесі болса, яғни L ^ =d/dx онда υ функциясы u функциясынан алынған туындыға тең болады. υ=u'.
Берілген функцияға сәйкес функциялар табу ережелері әртүрлі болатындықтан, операторлардың қасиеттері де әртүрлі болады. Кванттық механикада сызықтық операторлар қолданылады. L ^ операторын сызықтық оператор деп атайды, егер қарастырылып отырған көптеген функциялардың ішінен кез-келген u 1 және u 2 функциялары үшін және кез-келген С 1 және С 2 тұрақты сандар үшін мынадай теңдік орындалатын болса
L ^ (С 1 u 1 + С 2 u 2 ) = С 1 L ^ u 1 + С 2 L ^ u 2 (1)
Егер кез-келген u функциясы үшін мынадай теңдіктер орындалатын болса
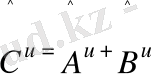 , С
^
1
u=A
^
1
u-B
^
1
u, С
^
2
u= A
^
2
(B
^
2
u) (2)
, С
^
1
u=A
^
1
u-B
^
1
u, С
^
2
u= A
^
2
(B
^
2
u) (2)
Онда С ^ , С ^ 1 , С ^ 2 операторларын сәйкес, А ^ және В ^ операторларының қосындысының, А ^ 1 және В ^ 1 операторларының айырмасының, А ^ 2 және В ^ 2 операторларының көбейтіндісінің операторлары деп атайды да, оларды былай жазады:
C ^ = A ^ +B ^ , С ^ 1 = A ^ 1 -B ^ 1 , С ^ 2 = A ^ 2 B ^ 2 (3)
Операторлардың қосындысы мен айырмасының алгебралық қасиеттері сандардың қосындысы мен айырмасының алгебралық қасиеттеріне ұқсас, олардың мүшелерінің орнын ауыстыруға және жинақтауға т. с. с. болады. Ал операторлардың көбейтіндісінің алгебралық қасиеттері сандар көбейтіндісінің алгебралық қасиеттерінен басқаша; операторлардың көбейтінділерінің мәндері олардың көбейткіштерінің орын ауыстыруына байланысты:
A ^ B ^ B ^ A ^ (4)
Яғни, жалпы алғанда операторлардың көбейтіндісі коммутативті емес. Мысалы, А ^ операторын х координатаға көбейту, ал В ^ операторы х координатасы бойынша туынды алу ережелері болсын, яғни
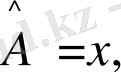
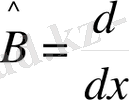
Сонда
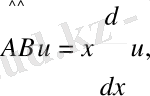
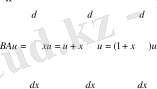
Осыдан
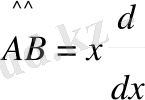
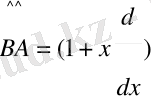 болады,
болады,
Сондықтан
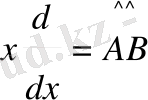
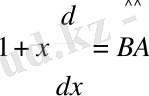
Операторлар А ^ және В ^ коммутативті деп аталады, егер олардың көбейтіндісі көбейткіштердің орналасу ретіне байланысты болмаса, яғни А ^ В ^ =В ^ А ^ .
Егер А ^ жәнеВ ^ операторлары мынадай теңдікті қанағаттандырса А ^ В ^ =-В ^ А ^ онда бұл операторларды антикоммутативті операторлар деп атайды.
Операторлар
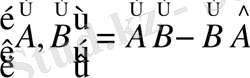 (5)
(5)
 және
және
 операторларының коммутаторы деп аталады. Ал егер олардың көбейтіндісі орындарын ауыстырғанда да шамалары өзгермесе, онда ондай операторларды коммутаторлы деп атайды.
операторларының коммутаторы деп аталады. Ал егер олардың көбейтіндісі орындарын ауыстырғанда да шамалары өзгермесе, онда ондай операторларды коммутаторлы деп атайды.
А ^ В ^ +В ^ А ^ операторын А ^ және В ^ операторының антикоммутаторы деп атайды да оны былай белгілейді:
А ^ В ^ +В ^ А ^ =[А ^ ; В ^ ] (6)
 операторы бірлік деп аталады, егер ол кез-келген функция үшін келесі теңдік орындалса:
операторы бірлік деп аталады, егер ол кез-келген функция үшін келесі теңдік орындалса:
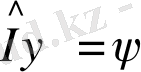
f(x) және g(x) функцияларының скаляр көбейтіндісі деп аталады,
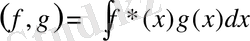
Векторлары үшін скаляр көбейтінді деп ψ п кеңістіктің Е п қатынасын анықтайық;
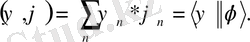 (7)
(7)
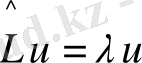 (8)
(8)
Онда, λ - L ^ операторының меншікті мәні, ал u - L ^ операторының λ меншікті мәніне сәйкес меншікті функциясы деп аталады. Бұдан былай операторды және оның меншікті мәнін бір әріппен белгілейтін боламыз:
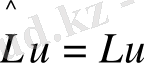 (8')
(8')
Оператордың меншікті мәндерінің жиынтығын оның спектрі деп атайды. Егер L ^ операторы сызықтық дифференциалды оператор болса, оның спектрлерінің үздіксіз де және үздік-үздік болатындығы да математикада дәлелденген.
Егер ψ және φ кез-келген функциялары үшін келесі қатынас орындалса:
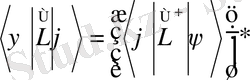 (9)
(9)
онда
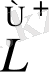 операторы
операторы
 операторына түйіндес деп аталады.
операторына түйіндес деп аталады.
Келесі операторлардың түйіндестік қасиеттерін қарастырайық:
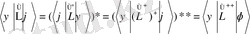
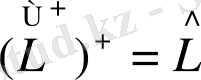
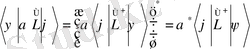
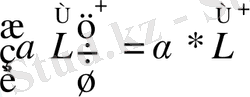
Немесе

Егер
 операторы өзінің
операторы өзінің
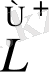 түйіндес операторымен бірге болса, онда ол эрмитті деп аталады.
түйіндес операторымен бірге болса, онда ол эрмитті деп аталады.
Сондықтан эрмитті деп
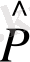 және
және
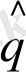 операторлары айтылады.
операторлары айтылады.
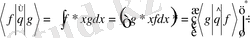
Кез-келген
 операторын келесі түрде жазуға болады:
операторын келесі түрде жазуға болады:
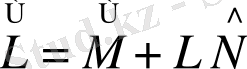 (10)
(10)
Мұндағы:
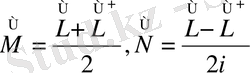
Эрмитті. Бұл шамаларды, яғни
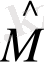 және
және
 анықтамаларын
анықтамаларын
 операторының эрмитті және антиэрмитті бөлшектері деп атайды.
операторының эрмитті және антиэрмитті бөлшектері деп атайды.
Эрмитті операторлардың көбейтіндісі эрмитті оператор деп аталады, егер операторлары коммутаторлы болса:
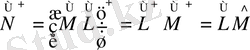 (11)
(11)
Операторларды қосу және көбейту
Егер
 және
және
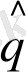 - операторлары, олар екі физикалық шамаларға ƒ және q жауап берсе, онда ƒ+ q суммаларына
- операторлары, олар екі физикалық шамаларға ƒ және q жауап берсе, онда ƒ+ q суммаларына
 +
+
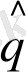 операторлары жауап береді.
операторлары жауап береді.
Кванттық механикада әр түрлі шамаларды қосу, олардың өлшемінің шамаларының біртекті немесе біртекті еместігінен тәуелді.
Егер ƒ және q шамалары біртекті өлшенетін болса, онда
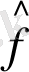 және
және
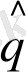 операторлары да
операторлары да
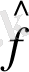 +
+
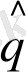 операторларының қосындысына тең.
операторларының қосындысына тең.
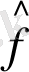 +
+
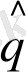 операторларының функциясы мен мағынасына келер болсақ, онда олар ƒ және q шамаларына еш қатыстары жоқ.
операторларының функциясы мен мағынасына келер болсақ, онда олар ƒ және q шамаларына еш қатыстары жоқ.
Анығырақ айтсақ, егер
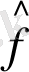 және
және
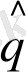 операторлары - эрмитті болса, онда
операторлары - эрмитті болса, онда
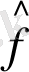 +
+
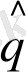 операторлары да эрмитті болады.
операторлары да эрмитті болады.
Келесі теореманы қарастырайық:
Ал енді қайтадан ƒ және q - біртекті өлшенетін шама болсын. Олардың суммаларының анықтамаларына қарап, олардың жеке анықтамасын енгізуге болады ƒ және q. Оңай көруге болады, бұндай шамаға оператор сәйкес келеді. Осындай оператор математикалық түрде
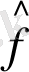 және
және
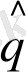 . Шынында да, егер Ψ
n
- жалпы оператордың функциясы болса
. Шынында да, егер Ψ
n
- жалпы оператордың функциясы болса
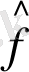 және
және
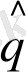 , онда:
, онда:
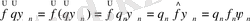
болады.
Операторлардың көбейтіндісін
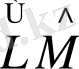 операторы анықтайды, ψ функциясына әрекеті тізбектей әрекет етеді
операторы анықтайды, ψ функциясына әрекеті тізбектей әрекет етеді
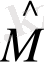 операторының ψ-ға, одан кейін
операторының ψ-ға, одан кейін
 операторының
операторының
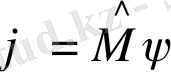 . Ақыр соңында олардың көбейтіндісі орындарының ауыстыруларына байланысты:
. Ақыр соңында олардың көбейтіндісі орындарының ауыстыруларына байланысты:
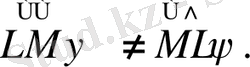 (12)
(12)
2. Динамикалық айнымалыларды /физикалық шамаларды/ сызықтық операторлар түрінде өрнектеу.
2. 1. Координаттар операторы
Толқындық функцияның физикалық мағынасына түсініктеме бергенде айтқанымыздай
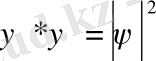 шамасы бөлшектің белгілі бір уақыт мезетінде кеңістіктің берілген бір ауданында болуының ықтималдығын көрсетеді. Сондықтан х координатының орташа мәнін былай есептеуге болады:
шамасы бөлшектің белгілі бір уақыт мезетінде кеңістіктің берілген бір ауданында болуының ықтималдығын көрсетеді. Сондықтан х координатының орташа мәнін былай есептеуге болады:
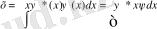 (13)
(13)
Осы өрнекті ықтималдық теориясы бойынша өрнектелетін динамикалық айнымалының орташа мәнін анықтайтын (12) өрнекпен салыстыра отырып х координатасының операторы ретінде осы координатаға көбейту операторын алу керек, яғни х операторын кейбір функцияға қолдану, осы функцияны х координатасына көбейту болып табылады. Осыған ұқсас у және z координаттарының операторында осы координаттарға көбейту болып табылады.
Сонымен
 (14)
(14)
2. 2. Импульс операторы
Импульс операторын анықтау үшін де-Бройль жорамалы бойынша импульсі Р
х
еркін бөлшекті толқындық саны
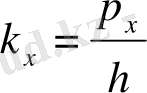 жиілігі
жиілігі
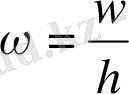 болатын жазық толқын ретінде қарастырып мынадай толқындық функциямен
болатын жазық толқын ретінде қарастырып мынадай толқындық функциямен
 (15)
(15)
сипаттауға болатындығын ескерейік. Сонда осы толқындық функция импульс операторының меншікті мәнін анықтайтын мына теңдеуді қанағаттандыруы қажет
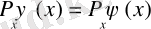 (16)
(16)
Осы өрнекті қанағаттандыру үшін импульс операторы мынадай болу керек
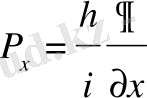 (17)
(17)
Өйткені, осындай болса ғана (15) функция (16) теңдеуді қанағаттандырады. Оны былай дәлелдеуге болады.
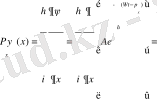 (18)
(18)

Сонымен (16) теңдеудің орындалатындығы дәлелденді. Осы сияқты р у , р z операторлары былай анықталады:
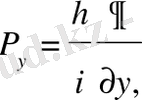
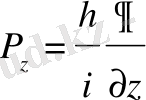 (19)
(19)
Импульс операторын вектор түрінде былай жазамыз:
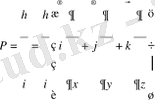 (20)
(20)
мұндағы
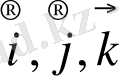 - бірлік векторлар.
- бірлік векторлар.
2. 3. Гамильтон операторы
Классикалық механикада Гамильтон функциясы деп жалпыланған импульспен жалпыланған координаттар арқылы өрнектелген толық энергияны айтады. Бір бөлшектің толық энергиясы оның кинетикалық энергиясымен потенциалдық энергиясының қосындысына тең
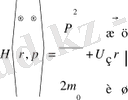 (21)
(21)
мұндағы
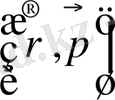 - Гамильтон функциясы.
- Гамильтон функциясы.
Кванттық механикада Гамильтон функциясына Гамильтон операторы сәйкес келу керек. Оны (21) өрнектегі Р импульстің орнына (20) өрнектен иимпульс операторын қою арқылы табамыз.
Сонда
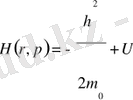 (22)
(22)
Толқындық функция Ψ толығымен кванттық механикадағы функциялық жүйенің күйін анықтайды. Бұл дегеніміз, бұл функцияның қызметі белгілі бір уақытта жүйенің бүкіл күйін сипаттап қоймай, оның келер уақыттағы моментін анықтайды.
Толық түрдегі жазылуы:
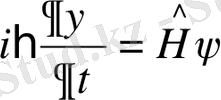 (23)
(23)
Мұндағы
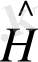 - сызықтық оператор,
- сызықтық оператор,
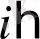 көбейткіші белгілі бір мақсатпен енгізілген тұрақты.
көбейткіші белгілі бір мақсатпен енгізілген тұрақты.
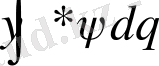 интегралы тұрақты болғандықтан, уақыттан тәуелді емес, онда:
интегралы тұрақты болғандықтан, уақыттан тәуелді емес, онда:
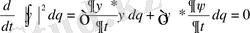 (24)
(24)
Осында (1) тендікті қойсақ және бірінші интегралда қолдансақ:
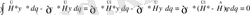
Бұл теңдік тек анықталған Ψ функциясы үшін орындалатын болса, онда осы жерден,
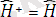
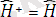 яғни оператор
яғни оператор
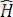
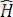 эрмитті.
эрмитті.
Оның қандай физикалық шамаға келетінін анықтайық. Ол үшін толқындық функцияны қолданайық.
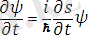
Бұл теңдікті (1) теңдігімен салыстырып, біздің осыдан көретініміз, ол шектік жағдайда
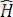
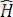 операторы жай көбейтінді
операторы жай көбейтінді
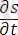
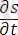 сәйкес келетінін көреміз. Бұл дегеніміз, соңғысы бұл сол баяғы функцияның шамасы, әйтеуір
сәйкес келетінін көреміз. Бұл дегеніміз, соңғысы бұл сол баяғы функцияның шамасы, әйтеуір
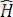
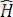 операторы.
операторы.
2. 4. Толық энергия операторы
Бөлшектің толық энергиясы W операторын, оның меншікті мәні бөлшектің толық энергиясы W-ға тең болатындай етіп таңдап алу керек. Ол үшін W операторының меншікті мәнін анықтайтын мына теңдеуді
 (25)
(25)
(16) -өрнекпен берілген толқындық функция қанағаттандыруы керек. Ол үшін W операторы мынадай болу қажет
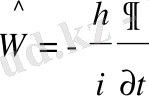 (26)
(26)
Осыны импульс операторын дәлелдегендей көрсетуге болады.
2. 5. Импульс моменті операторы
Классикалық механикада бөлшектің импульс моменті деп, бөлшектің радиус-векторымен импульс векторының векторлық көбейтіндісіне тең векторлық шаманы айтады, яғни
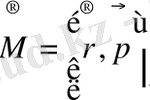 (27)
(27)
немесе, координаттар осьтеріне проекциясы
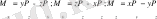 (28)
(28)
Кванттық механикада импульс моменті проекцияларына сәйкес олардың операторларын (18) және (20) өрнектерді пайдаланып былай жазамыз
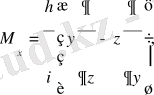
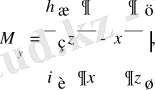
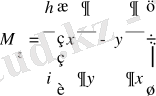 (29)
(29)
3. Бір мезгілде әртүрлі динамикалық айнымалыларды өлшеу шарттары
Кванттық механиканың үшінші постулатына сәйкес, динамикалық айнымалыларды өлшегенде оның нақты сан мәнін аламыз, сол уақытта, егер осы динамикалық айнымалыны өрнектейтін оператордың меншікті функциясы бөлшектердің күйін сипаттайтын толқындық функция болса. әртүрлі динамикалық айнымалылардың операторларының меншікті функциялары әртүрлі болғандықтан оларға сәйкес келетін меншікті мәндері де әртүрлі болады, сондықтан динамикалық айнымалыларды бір мезгілде өлшегенде бірдей сан мәндерінің шығуы мүмкін емес, яғни оларды бір мезгілде өлшеуге болмайды. Дегенмен де белгілі бір шарттар орындалса әртүрлі динамикалық айнымалыларды бір мезетте өлшеуге болады. Оның қажетті және жеткілікті шарты, осы динамикалық айнымалылардың операторларының коммутативтілігі. Осы шарттың орындалуының қажеттілігін былай дәлелдеуге болады.
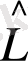 және
және
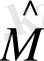 операторларының меншікті функциялары бірдей және осы операторлармен өрнектелетін динамикалық айнымалыларды бір мезетте өлшеуге болады деп есептейік. Сонда, операторлардың меншікті мәндері үшін теңдеу бойынша:
операторларының меншікті функциялары бірдей және осы операторлармен өрнектелетін динамикалық айнымалыларды бір мезетте өлшеуге болады деп есептейік. Сонда, операторлардың меншікті мәндері үшін теңдеу бойынша:
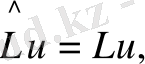
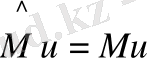 (30)
(30)
Сонда
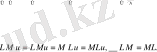
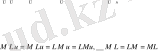
Осыдан
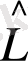 және
және
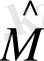 операторларымен өрнектелетін динамикалық айнымалыларды бір мезетте өлшеу үшін олардың операторларының коммутативті болу қажеттілігі дәлелденді, яғни
операторларымен өрнектелетін динамикалық айнымалыларды бір мезетте өлшеу үшін олардың операторларының коммутативті болу қажеттілігі дәлелденді, яғни
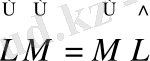 (31)
(31)
Енді осы шарттың жеткілікті екендігін дәлелдейік. Ол үшін
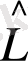 және
және
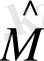 операторлары коммутативті деп есептейік, сонда егер осы операторлардың біреуінің, мысалы
операторлары коммутативті деп есептейік, сонда егер осы операторлардың біреуінің, мысалы
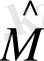 операторының меншікті функциясын u деп белгілейік, яғни
операторының меншікті функциясын u деп белгілейік, яғни
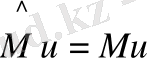 (32)
(32)
болса онда (31) өрнекке сәйкес былай жазуға болады:
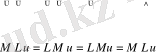 (33)
(33)
Осыдан
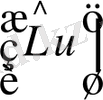 функциясы
функциясы
 операторының М меншікті мәніне сәйкес келетін меншікті функция болатындығын көреміз. Ал (32) өрнек бойынша М меншікті мәніне сәйкес келетін меншікті функция u. Сондықтан u және
операторының М меншікті мәніне сәйкес келетін меншікті функция болатындығын көреміз. Ал (32) өрнек бойынша М меншікті мәніне сәйкес келетін меншікті функция u. Сондықтан u және
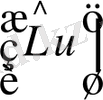 функциялары
функциялары
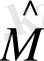 операторының М меншікті мәніне сәйкес келетін меншікті функциялары болады, оларды бір L санымен белгілесек, онда (33) өрнек бойынша
операторының М меншікті мәніне сәйкес келетін меншікті функциялары болады, оларды бір L санымен белгілесек, онда (33) өрнек бойынша
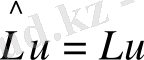 (34)
(34)
Бұл теңдік u функциясы
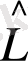 операторының да меншікті функциясы болатындығын көрсетеді. Сонымен
операторының да меншікті функциясы болатындығын көрсетеді. Сонымен
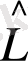 және
және
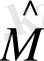 операторларының ортақ меншікті функцияларының болатындығын және осы операторларға сәйкес динамикалық айнымалыларды бір мезетте өлшеуге болатындығын көреміз. Осымен мынандай теорема дәлелденді:
операторларының ортақ меншікті функцияларының болатындығын және осы операторларға сәйкес динамикалық айнымалыларды бір мезетте өлшеуге болатындығын көреміз. Осымен мынандай теорема дәлелденді:
Егер динамикалық айнымалыларды өрнектейтін операторлар коммутативті болса, онда осы айнымалыларды бір мезетте өлшеуге болады.
4. Динамикалық айнымалылардың орташа мәндерінің уақыт бойынша өзгерісі және сақталу заңдары
Жалпы алғанда динамикалық айнымалылардың орташа мәндері уақыт бойынша өзгереді. Белгілі бір
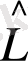 операторымен өрнектелетін L динамикалық айнымалының орташа мәнін былай анықтауға болады:
операторымен өрнектелетін L динамикалық айнымалының орташа мәнін былай анықтауға болады:

Осы теңдіктің екі жағынан уақыт бойынша туынды алайық
 (35)
(35)
егер толық теңдеу
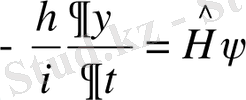 және
және
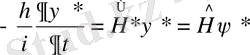 (36)
(36)
екендігін ескерсек, онда (35) теңдеуді мынадай түрде жазуға болады:
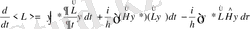 (37)
(37)
Гамильтон операторы
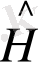 өзара түйіндес оператор болғандықтан теңдіктің оң жағындағы екінші мүшені былай түрлендіруге болады
өзара түйіндес оператор болғандықтан теңдіктің оң жағындағы екінші мүшені былай түрлендіруге болады
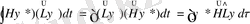 (38)
(38)
Осы (38) - өрнекті (37) теңдеуге қойсақ онда
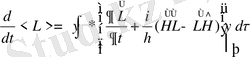 (39)
(39)
Сонымен динамикалық айнымалылардың орташа мәндерінен уақыт бойынша алған туындыны (39) - теңдеудің оң жағындағы интегралдың астындағы жақшаның ішінде тұрған оператордың орташа мәні деп қарастыруға болады. Сондықтан осы операторды қарастырып отырған
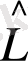 оператордың уақыт бойынша туындысының анықтамасы ретінде қарастыруға болады да, оны
оператордың уақыт бойынша туындысының анықтамасы ретінде қарастыруға болады да, оны
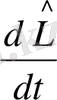 деп белгілесек, онда
деп белгілесек, онда
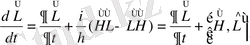 (40)
(40)
Мұндағы
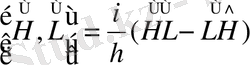 (41)
(41)
Классикалық механикадағы Пуассон жақшасына ұқсас осы (41) өрнекті Пуассонның кванттық жақшасы деп атайды. Осы ұқсастықты мынадан көруге болады. Классикалық механикада кез келген динамикалық айнымалы L координат, импульс және уақыттың функциясы болады, яғни L=L(x i , p i , t) . Сондықтан
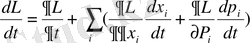 (42)
(42)
Гамильтон теңдеуі бойынша:
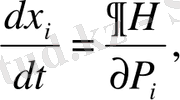
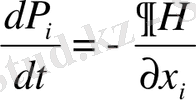 (43)
(43)
Екенін ескерсек онда (42) өрнек мына түрге келеді
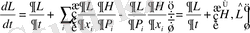 (44)
(44)
Мұндағы
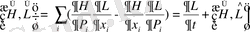 (45)
(45)
Пуассон жақшасы, ал Н-Гамильтон функциясы.
Егер
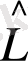 операторы және L уақытқа тікелей тәуелді болмаса, онда (40) және (44) теңдеулерден
операторы және L уақытқа тікелей тәуелді болмаса, онда (40) және (44) теңдеулерден
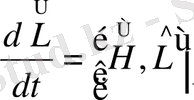 (46)
(46)
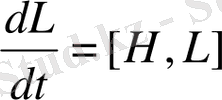 (47)
(47)
болады. Классикалық және кванттық өрнектердің арасындағы ұқсастықты тереңірек қарастыруға болады. (47) өрнекпен берілген классикалық теңдеу динамикалық айнымалылардың уақыт бойынша өзгерісін көрсетеді де осы динамикалық айнымалы үшін қозғалыс теңдеуі болады. Шынында да, егер (47) өрнектегі L айнымалыны х еоординатасымен, содан кейін Р импульспен алмастырсақ:

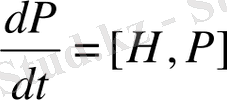 (48)
(48)
(45) Пуассон жақшасы бойынша:
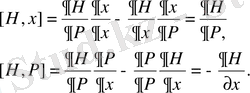
осы өрнектерді (48) теңдеуге қойсақ, онда
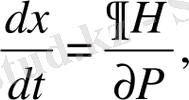
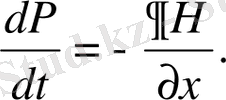 (49)
(49)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz