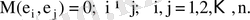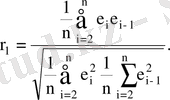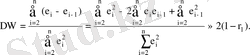Ең кіші квадраттар регрессиясында мультиколлинеарлық пен автокорреляция: себептері, анықтау және жою әдістері


Жоспар:
- Мультиколлинеарлық
- Мультиколлинеарлықты анықтау және жою
- Автокорреляцияның пайда болуы
- Автокорреляцияны айқындау және жою
1 Мультиколлинеарлық
Ең кіші квадраттар әдісін пайдаланып жиындық регрессия моделін құруда басты мәселелердің бірі мультиколлинеарлық болып табылады. Регрессия теңдеуінде екі немесе бірнеше түсіндіруші айнымалылардың корреляциялық байланысын мультиколлинеарлық деп атайды. Мысалы: түсіндіруші айнымалылар құрамына қолда бар кіріс және тұтыну кіретін болса, онда олардың екеуіде корреляциялық байланыста болады. Егер түсіндіруші айнымалылар арасында қатал функционалдық тәуелділік болса, онда мультиколлинеарлық толық (жетілген) деп аталады. Ең кіші квадраттар әдісімен көптік сызықтық регрессия моделін құрған кезде ең күрделі мәселе мультиколлинеарлық- бір немесе бірнеше түсіндірмелі айнымалының сызықтық өзарабайланысы. Егер түсіндірмелі айнымалылар қатаң функционалдық тәуелділікпен байланысса, онда жетілген мультиколлинеарлық туралы айтуға болады.
Мультиколлинеарлықтың бар екенін бірнеше белгісі бойынша орнатуға болады.
1. Детерминация коэффициенті
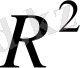 жеткілікті жоғары мән алады, бірақ регрессияның кейбір коэффициенттері статистикалық мәнсіз, яғни олардың t-статистиксы өте төмен.
жеткілікті жоғары мән алады, бірақ регрессияның кейбір коэффициенттері статистикалық мәнсіз, яғни олардың t-статистиксы өте төмен.
2. Мәнсіз түсіндірмелі айнымалылар арасындағы жұп корреляция едәуір жоғары. Бірақ бұл белгі тек екі түсіндірмелі айнымалы арасында ғана сенімді болады. Оның саны үлкен болған сайын жеке корреляция коэффициенттерін қолданған маңызды.
3. Жеке корреляция коэффициенттері жоғары.
Жеке корреляция коэффициенттері екі айнымалы арасындағы сызықтық тәуелділік күшін басқа айнымалылардың әсерінсіз анықтайды. Бірақ көпөлшемді байланыстарды зерттеген кезде жұп корреляция коэффициенттері екі айнымалы арасындағы байланыс сапасы туралы қате сипаттама беруі мүмкін. Мысалы екі айнымалы Х және Уарасындағы байланыстың корреляция коэффициенті жоғары болуы ықтимал, ол бір айнымалының өзгеруіне сәйкес екінші айнымалы өзгереді деген сөз емес, бірақ ол моделде есептелген немесе есептелмеген айнымалылар әсерінен болуы мүмкін. Сондықтан қарастырылып отырған екі айнымалыны басқа факторлар әсерінен арылтып, нақты екі фактордың сызықтық байланыс күшін есептеу қажет. Басқа факторлар әсерінен тазартылған екі айнымалы арасындағы корреляция коэффициенті жеке корреляция коэффициенті деп аталады.
Мультиколлинеарлық тек қана жиындық регрессия моделінің мәселесі болуы мүмкін. Регрессия моделі мына түрде берілсін
(1)
Түсіндіруші айнымалылар арасында қатал сызықтық байланыс болсын
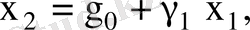
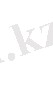
(2)
онда (1) теңдеуін мына түрде жазуға болады
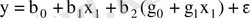
немесе
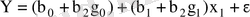
 деп белгілеп, қос сызықтық регрессия теңдеуін аламыз
деп белгілеп, қос сызықтық регрессия теңдеуін аламыз
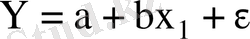
(3)
Ең кіші квадраттар әдісін пайдаланып
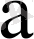 және
және
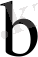 коэффициенттерін табу қиын емес.
коэффициенттерін табу қиын емес.
(4)
(4) жүйе
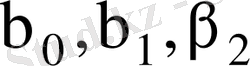 белгісіздерден тұрады. Мұндай жүйенің көп жағдайда шексіз көп шешімі болады. Ендеше толық мультиколлинеарлық регрессия теңдеуінің коэффициенттерін бірмәнді анықтауға және
белгісіздерден тұрады. Мұндай жүйенің көп жағдайда шексіз көп шешімі болады. Ендеше толық мультиколлинеарлық регрессия теңдеуінің коэффициенттерін бірмәнді анықтауға және
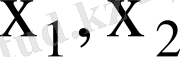 түсіндіруші айнымалылардың
түсіндіруші айнымалылардың
 тәуелді айнымалыға әсер ету мөлшерін анықтауға мүмкіндік бермейді.
тәуелді айнымалыға әсер ету мөлшерін анықтауға мүмкіндік бермейді.
Бұл жағдайда аталған коэффициенттер туралы негізделген статистикалық тұжырым жасауға болмайды. Сондықтан мультиколлинеарлық болған жағдайда регрессияның коэффициенттері және регрессия теңдеуі туралы тұжырым сенімді емес. Толық мультиколлинеарлық көбіне теориялық мысал ретінде кездеседі. Нақты жағдайларда түсіндіруші айнымалылар арасындағы корреляциялық тәуелділік тығыз, ал функционалдық тәуелділік қатал емес болады. Мұндай тәуелділік толық емес (жетілмеген) мультиколлинеарлық деп аталады.
2 Мультиколлинеарлықты анықтау
Мультиколлинеарлықты анықтаудың бірнеше белгілері бар:
- детерминация коэффициенті өте жоғары, бірақ регрессияның кейбір коффициенттері статистикалық маңызды емес.
- маңызды емес түсіндіруші айнымалылар арасындағы қос корреляция жоғары.
- дербес корреляция коэффициенттері жоғары. Дербес корреляция коэффициенті деп басқа айнымалылар әсер етпейтін екі айнымалының арасындағы корреляция коэффициентін атайды.
- қосымша тығыз регрессия. Кез келген түсіндіруші айнымалы басқа түсіндіруші айнымалылардың сызықтық комбинациясы болуы салдарынан мультиколлинеарлық пайда болады.
3 Мультиколлинеарлықты жою
Егер моделдің негізгі міндеті моделдегі тәуелді айнымалының мәндерін болжау болса, онда детерминация коэффициенті жоғары болған жағдайда мультиколлинеарлық бар болуы моделдің болжамдық сапасына әсер етпейді. Кез келген жағдайда мультиколлинеарлықты жоюдың нақты бір әдісі жоқ. Мультиколлинеарлықты жоюдың әдістері:
1) моделдегі бір немесе бірнеше айнымалыны жою;
2) қосымша мәліметтер алу немесе жаңа таңдама алу;
3) моделдің спецификациясын өзгерту;
4) кейбір параметрлер туралы алдын - ала белгілі ақпараттарды пайдалану;
5) айнымалыларды түрлендіру.
3 Автокорреляцияның пайда болуы
Автокорреляция (дәйекті корреляция) уақыт бойынша (уақыт қатары) реттелген немесе кеңістіктегі (қиылысқан мәліметтер) бақыланған көрсеткіштер арасындағы корреляция ретінде анықталады. Қалдықтар автокорреляциясы (ауытқу) регрессиялық талдауда уақыт қатарындағы мәліметтерді қолданғанда пайда болады. Қиылысқан мәліметтерді қолданған кезде автокорреляция (кеңістіктік корреляция) сирек кездеседі.
Автокорреляция туындайтын негізгі себептерге, спецификация қателігін, экономикалық көрсеткіштердің инерттілігін, өрмек эффектісін, мәліметтерді тегістеуді жатқызуға болады.
Спецификация қателігі. Моделде маңызды түсіндірмелі айнымалыны есепке алмау немесе тәуелділік түрін дұрыс таңдамау бақылау нүктелерінің регрессия сызығынан жүйелі ауытқуға алып келеді де, автокорреляцияның туындауына себеп болады.
Инерция. Көптеген экономикалық көрсеткіштер (мысалы, инфляция, жұмыссыздық, ҰІӨ және т. б. ) іскерлік белсенділігі толқынтәріздес болатын, анықталған циклды процесс. Шындығында экономикалық жоғарылау жұмыс санының өсуіне, инфляцияның қысқаруына, ҰІӨ артуына жетелейді және т. б. Бұл өсу нарық конъюнктурасының өзгеруіне дейін немесе кейбір экономикалық сипаттамалар өсуді баяулатқанға дейін жалғасады, содан соң тоқтайды және қайтадан қарастырылған көрсеткіштер қозғалысқа енеді. Қандай жағдайда да бұл трансформация тез жүрмейді, белгілі шамадағы инерттілікте болады.
Өрмек э ффектісі. Көптеген өндірістік және басқа сфераларда экономикалық көрсеткіштер экономикалық жағдайдың өзгеруін кешігіп сезеді (уақыт лагы) . Мысалы, ауылшаруашылық өнімдеріне ұсыныс бағаның өзгеруіне кешігіп назар салады (өнім пісіп жетілген мерзімге тең) . Ауылшаруашылық өнімдерінің өткен жылғы үлкен бағасы ағымдағы жылда көп өндіруге алып келеді, нәтижесінде оның бағасы төмендейді т. б.
Мәліметтерді тегістеу. Кейбір ұзақ уақыт мерзімінде мәліметтердің орта мәні алынады, ол оны құраушы интервалдарға сәйкес келеді. Бұл қарастырылып отырған мерзімде белгілі тербелістерді тегістеуге алып келеді де автокорреляцияның туындауына себеп болады.
Регрессия коэффициенттерінің маңыздылығын және регрессия теңдеуінің сапасын тексеруден басқа регрессия параметрлерінің бағасын жылжымаған және тиімді болуын қамтамасыз ететін Гаусс-Марков шарттарының орындалуын тексеру қажет. Гаусс-Марковтың үшінші шартын (әртүрлі бақылаулардағы кездейсоқ мүшелердің тәуелсіздігі) оның бірінші шарты
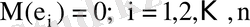 орындалғанда былай жазуға болады.
орындалғанда былай жазуға болады.
Осы шарт орындалмау нәтижесінде, яғни кездейсоқ мүшелердің арасында байланыс болса, автокорреляция пайда болады. Автокорреляция оң болған жағдайда бірқатар тізбектелген бақылауларда кездейсоқ мүше тәуелді айнымалы мәнін бір бағытта жылжытады; сосын бірнеше тізбектелген бақылауларда қарама-қарсы бағытқа жылжытады; сосын қайтадан бастапқы бағытпен жылжытады.

Сурет 9 − Оң автокорреляция.
Экономикада оң автокорреляция іскерлік белсенділік циклымен, әсері регрессия теңдеуінің кездейсоқ мүшесімен айқындалатын мерзімдік өзгерістермен байланысты болуы мүмкін. Теріс автокорреляцияда
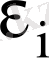 кездейсоқ шамасы қолдануы қарама-қарсы таңбалы
кездейсоқ шамасы қолдануы қарама-қарсы таңбалы
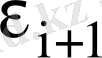 кездейсоқ мүшенің қолданысымен ауыстырылады.
кездейсоқ мүшенің қолданысымен ауыстырылады.
Сурет 10 − Теріс автокорреляция.
Әдетте экономикада оң автокорреляция пайда болуы мүмкін, әсіресе уақытша қатарлар үшін. Бақылаулар жиі болу әсерінен автокорреляция пайда болуы ықтимал.
4 Автокорреляцияны айқындау
Регрессия коэффициенттерінің нақты мәндері белгісіз болғандықтан әрбір бақылауда кездейсоқ мүше
 -ның мәндері де белгісіз. Сондықтан тек қана
-ның мәндері де белгісіз. Сондықтан тек қана
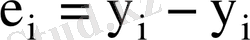 ауытқулардың өзара корреляциялық байланысын тексеруге мүмкіндік бар. Бірінші ретті автокорреляция коэффициенті
ауытқулардың өзара корреляциялық байланысын тексеруге мүмкіндік бар. Бірінші ретті автокорреляция коэффициенті
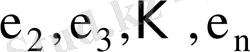 және оларға сәйкес
және оларға сәйкес
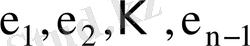 ауытқулар таңдама корреляция коэффициенті
ауытқулар таңдама корреляция коэффициенті
(бұл жерде
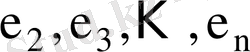 және
және
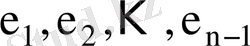 үшін таңдаманың ортасы салыстырмалы аз шама, сондықтан ескерілмеген)
үшін таңдаманың ортасы салыстырмалы аз шама, сондықтан ескерілмеген)
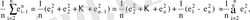
онда автокорреляция коэффициенті
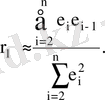
Автокорреляцияны айқындау үшін Дарбин-Уотсон статистикасы қолданылады.
Автокорреляция оң болғанда
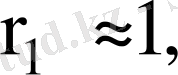 сондықтан
сондықтан
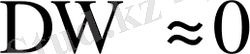 болады. Автокорреляция теріс болғанда
болады. Автокорреляция теріс болғанда
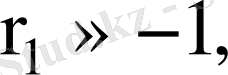 сондықтан
сондықтан
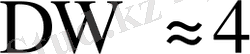 болады. Автокорреляция жоқ болғанда
болады. Автокорреляция жоқ болғанда
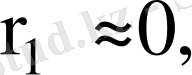 онда
онда
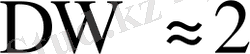 болады. Дарбин -Уотсон статистикасының кризистік мәндері түсіндіруші айнымалылармен қатар таңдамада қабылдайтын мәндеріне тәуелді. Сондықтан Дарбин -Уотсон статистикасының
болады. Дарбин -Уотсон статистикасының кризистік мәндері түсіндіруші айнымалылармен қатар таңдамада қабылдайтын мәндеріне тәуелді. Сондықтан Дарбин -Уотсон статистикасының
 және
және
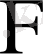 статистикалардан өзгешелігі оның
статистикалардан өзгешелігі оның
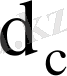 кризистік мәндерінің кестесін құруға болмайды.
кризистік мәндерінің кестесін құруға болмайды.
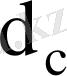 табу үшін оның
табу үшін оның
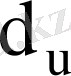 жоғарғы және
жоғарғы және
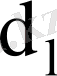 төменгі шекараларын көрсету керек.
төменгі шекараларын көрсету керек.
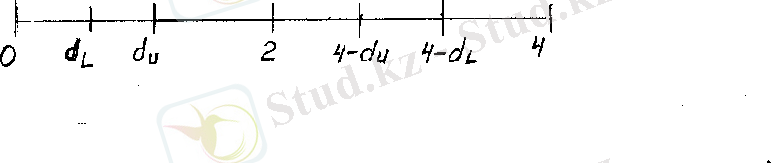 Сурет 11 − DW мәндерінің кризистік нүктелерінің шекарасы.
Сурет 11 − DW мәндерінің кризистік нүктелерінің шекарасы.
Автокорреляцияда келесі нөлдік және альтернативті болжамдар қойылады:
 оң автокорреляция жоқ;
оң автокорреляция жоқ;
 : оң автокорреляция бар.
: оң автокорреляция бар.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz