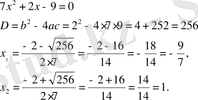Бүтін сандар жиынында анықталмаған теңдеулерді шешу әдістері

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... ... 3
1 АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ... ... ... ... ... ... . ... 7
1.1Дәрежелік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... ... ... .. .. ... ...7
1.2 Көрсеткіштік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... ... ... ... 11
1.3 Логарифмдік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... .. .. ... ... 25

2 АНЫҚТАЛМАҒАН ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 28
2.1Теңдеу және оның бүтін шешімі туралы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 35
2.2 Бірнеше белгісізі бар теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...37
2.3 Анықталмаған теңдеудің түбірлерінің және оның бүтін шешімі болмайтындығын ың белгілері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...47
2.4 Анықталмаған теңдеудің түбірлерінің жалпы формуласы және дербес түрі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ...49
2.5 Екінші дәрежелі теңдеулерді анықтауыштар әдісімен шешу ... ... ... ... ... 63
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..75
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 76

Қазақстан Республикасының Президенті Н.Ә.Назарбаев «Қазақстан-2030» стратегиялық бағдарламасында «Еліміздің білім беру жүйесінің дамуы – жаңа ақпараттық технологиялар мен компьютерлердің қолданылу деңгейіне, шығармашыл білімнің қалыптастырылатындығына, оның әлеуеттік мүмкіндігінің күшеюіне байланысты» деп атап көрсетті [1]. Сондай-ақ дәстүрлі халыққа Жолдауында: «Білім беру жүйесінде заманауи әдістемелерді қолдану қажет» делінген болатын [2]. Осыған орай Қазақстан Республикасының білім және ғылым министрлігі тарапынан математика пәнін тереңдетіп оқытуда, оның ішінде элективті курстарда оқушыларға сапалы білім беру мәселелері қамтылған [3]. Жалпы орта мектептің математика пәні бойынша мемлекеттік жалпыға міндетті стандартында бұл пәннің саласында онымен іргелес өзге де ғылым салаларындағыдай жаңа білім көлемі жедел қарқынмен дамып, отырғаны айтылып, осы нормативтік құжаттың мақсат-міндеттерін анықтауда ескерілген қоғамдық өзгерістің бірінде былай делінген: «...Қоғамның жоғары деңгейде математиканы қолдануы - математиканы оқыту барысында оқушылардың логикалық ойлау қабілеттерін арттыруды талап етеді» [4].
Қазақстан Республикасында қазіргі уақыттағы экономика және әлеуметтік жағдайлардағы оң өзгерістер мен жетістіктер еліміздің білім беру жүйесін жетілдіруді талап етуде. Халықаралық стандарттар деңгейінде білім беруге қол жеткізу үшін математика пәнін оқытуда қолданылатын дәстүрлі әдістермен қатар, таңдау курстарында математика пәнін тереңдетіп оқытудың маңызы ерекше[5-6]. Әрине ол үшін, мемлекеттік стандартта көрсетілген есептермен қатар, күрделі есептерді оқушыларға үйрету қажет. Атап айтқанда, орта мектеп математикасында көп көңіл бөлінбейтін Диофанттық теңдеулерді үйретудің ролі айрықша болып табылады. Өйткені оқытуды ұйымдастыруда математика пәні мұғалімі оқушылардың логикалық ойлау қабілетін дамытуы, қажетті біліммен қамтамасыз етуі, олардың есеп шығаруы іскерліктері мен дағдыларын қалыптастыруы айтпаса да түсінікті. Оқыту сапасын арттыру, өмірмен практиканы байланыстыру да күн тәртібінен түскен емес. Оны шешудің бірден-бір жолы, Диофанттық теңдеулерді шешудің әдістемелік және дидактикалық негіздемесін жасауға келіп тіреледі.
Өйткені, анықталмаған теңдеулерді шешуге оқушыларды дағдыландыра отырып, материалды игеруге ғылымилық және логикалық ойлауын, есепті шешудің қандай да бір түріне шығармашылықпен қарау деңгейін дамытып, жетілдіре түседі.
Кезінде есептерді дәстүрлі және дәстүрлі емес тәсілдермен шешумен айналысқан А.Н.Леоньтевтің [7] еңбегінде оқушылардың логикалық ойлау қызметін дамытуы тиіс делінген. Ю.К.Бабанский[8-9], Г.В.Дорофеев[10-12], И.Ф.Шарыгин [13-14], Л.С.Выготский [15-17], В.А.Далингер [18], А.Г.Барышкин [19-20], А.М.Пышкало [21], А.П.Власова[22], Е.Д.Кулагин[23] ,М.К.Потапов[24], М.И.Сканави[25],

1 Қазақстан Республикасы жалпы орта білім берудің мемлекеттік жалпыға міндетті білім беру стандарттары. Жалпы орта білім. –Алматы: РОНД, 2002.-368 б.
2 Назарбаев Н.Ә. Қазақстан-2030. –Алматы,: Білім, 1997. -176 б.
3 Жалпы орта мектептің 5-11-сыныптың математика бағдарламалары. Астана, 2009. – 55 б.
4 Шарыгин И. Ф., Голубев В. И. Факультативный курс по мате-матике. Решение задач: Учебное пособие для 11 класса, М.: Просвещение, 2001.
5Кулагин Е. Д.3000 конкурсных задач по ма¬тематике. М., 2002.
Натяганов В. Л., Лужина Л. М. Методы решения задач с параметрами. Часть 1., М., 2004.
6Потапов М.К. и др. Математика. Методы решения задач. Для поступающих в вузы. М., 2005.
7Сканави М.И. Сборник задач по математике для поступающих в вузы: В 2 кн. Кн. 1. М., 2002.
8Корешкова ТА., Глазков Ю.А., Мирошин В.В. и др. Математика: Типовые тестовые задания. М., 2005.
9 Шарыгин И. Ф. Математика. Для поступающих в ВУЗы: Учебное пособие.- 4-е изд. – М.: Дрофа, 2002.
10 Шарыгин И. Ф., Голубев В. И. Решение задач: Учебное пособие для 11 класса общеобразовательных учреждений. – 2-е изд. – М.: Просвещение, .
11Авербух Б. Г., Рубинштейн А. И. Об определении степени ирешении уравнений и неравенств, содержащих показательно степенную функцию. // Математика в школе. – 1996.
12Шахно К.И. Сборник задач по элементарной математике повышенной трудности: Высшая школа, 1967.
13Норин А. В. Сборник задач по математике для поступающих в ВУЗы: Учебное пособие. – Спбю: Питер,2003.
14Колесникова С.И. Математика. Решение сложных задач Единого государственного экзамена. М. «АЙРИС – пресс», 2005.
15Родионов Е.М., Синякова С.Л. Математика. Пособие для поступающих в вузы. Учебный центр «Ориентир» МГТУ им. Н.Э. Баумана, М., 2009.
16 Қарабаев А. Қ. Жоғары сынып оқушыларының шығармашылық қабілетін дамытуға ықпал жасайтын стандарт емес есептер. Шымкент, 2003.
17 Варлаховский Ф.Л., Солодовников А.С. Задачник-практикум по алгебре.-М.. 1982.- Ч.1.
18 Туманов С.И. Элементарная алгебра.-М., 1960.
19 Окунев Л.Я. Высшая алгебра.- М., 1966.
20Оразбаев Б.М. Анықтауыштар теориясы.- Алматы, 1967.
21Окунов А.К. Квадратные функции, уравнения и неравенства.- М., 1966.

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

БҮТІН САНДАР ЖИЫНЫНДА АНЫҚТАЛМАҒАН ТЕҢДЕУЛЕРДІ
ШЕШУ ӘДІСТЕРІ

МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. . ... ... 3
1 АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ... ... ... ... ... ... . ... 7
1.1Дәрежелік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... ... ... . .. .. ... ...7
1.2 Көрсеткіштік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... .. . ... ... 11
1.3 Логарифмдік теңдеулер және оларды шешу әдістері ... ... ... ... ... ... .. .. ... ... 25

2 АНЫҚТАЛМАҒАН ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... ... .. 28
2.1 Теңдеу және оның бүтін шешімі туралы ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ...35
2.2 Бірнеше белгісізі бар теңдеулер ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ..37
2.3 Анықталмаған теңдеудің түбірлерінің және оның бүтін шешімі болмайтындығын ың белгілері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ..47
2.4 Анықталмаған теңдеудің түбірлерінің жалпы формуласы және дербес түрі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...49
2.5 Екінші дәрежелі теңдеулерді анықтауыштар әдісімен шешу ... ... ... ... ... 63
ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..75
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 76

КІРІСПЕ
Қазақстан Республикасының Президенті Н.Ә.Назарбаев Қазақстан-2030 стратегиялық бағдарламасында Еліміздің білім беру жүйесінің дамуы - жаңа ақпараттық технологиялар мен компьютерлердің қолданылу деңгейіне, шығармашыл білімнің қалыптастырылатындығына, оның әлеуеттік мүмкіндігінің күшеюіне байланысты деп атап көрсетті [1]. Сондай-ақ дәстүрлі халыққа Жолдауында: Білім беру жүйесінде заманауи әдістемелерді қолдану қажет делінген болатын [2]. Осыған орай Қазақстан Республикасының білім және ғылым министрлігі тарапынан математика пәнін тереңдетіп оқытуда, оның ішінде элективті курстарда оқушыларға сапалы білім беру мәселелері қамтылған [3]. Жалпы орта мектептің математика пәні бойынша мемлекеттік жалпыға міндетті стандартында бұл пәннің саласында онымен іргелес өзге де ғылым салаларындағыдай жаңа білім көлемі жедел қарқынмен дамып, отырғаны айтылып, осы нормативтік құжаттың мақсат-міндеттерін анықтауда ескерілген қоғамдық өзгерістің бірінде былай делінген: ...Қоғамның жоғары деңгейде математиканы қолдануы - математиканы оқыту барысында оқушылардың логикалық ойлау қабілеттерін арттыруды талап етеді [4].
Қазақстан Республикасында қазіргі уақыттағы экономика және әлеуметтік жағдайлардағы оң өзгерістер мен жетістіктер еліміздің білім беру жүйесін жетілдіруді талап етуде. Халықаралық стандарттар деңгейінде білім беруге қол жеткізу үшін математика пәнін оқытуда қолданылатын дәстүрлі әдістермен қатар, таңдау курстарында математика пәнін тереңдетіп оқытудың маңызы ерекше [5-6]. Әрине ол үшін, мемлекеттік стандартта көрсетілген есептермен қатар, күрделі есептерді оқушыларға үйрету қажет. Атап айтқанда, орта мектеп математикасында көп көңіл бөлінбейтін Диофанттық теңдеулерді үйретудің ролі айрықша болып табылады. Өйткені оқытуды ұйымдастыруда математика пәні мұғалімі оқушылардың логикалық ойлау қабілетін дамытуы, қажетті біліммен қамтамасыз етуі, олардың есеп шығаруы іскерліктері мен дағдыларын қалыптастыруы айтпаса да түсінікті. Оқыту сапасын арттыру, өмірмен практиканы байланыстыру да күн тәртібінен түскен емес. Оны шешудің бірден-бір жолы, Диофанттық теңдеулерді шешудің әдістемелік және дидактикалық негіздемесін жасауға келіп тіреледі.
Өйткені, анықталмаған теңдеулерді шешуге оқушыларды дағдыландыра отырып, материалды игеруге ғылымилық және логикалық ойлауын, есепті шешудің қандай да бір түріне шығармашылықпен қарау деңгейін дамытып, жетілдіре түседі.
Кезінде есептерді дәстүрлі және дәстүрлі емес тәсілдермен шешумен айналысқан А.Н.Леоньтевтің [7] еңбегінде оқушылардың логикалық ойлау қызметін дамытуы тиіс делінген. Ю.К.Бабанский[8-9], Г.В.Дорофеев[10-12], И.Ф.Шарыгин [13-14], Л.С.Выготский [15-17], В.А.Далингер [18], А.Г.Барышкин [19-20], А.М.Пышкало [21], А.П.Власова[22], Е.Д.Кулагин[23] ,М.К.Потапов[24], М.И.Сканави[25], Т.А.Корешкова[26], Д.Т.Письменный [27] және т.б. зерттеулерінде Диофанттық теңдеулерді шешу әдістерін оқушылардың меңгеретін біліміндегі логикалық ойлаудың маңызын атап көрсеткен.
Анықталмаған теңдеулерді шешу әдістерінің мәселесiне Ю.М.Колягин [28], Л.Н.Нуритдинов [31], В.Г.Болтянский [32], В.В.Афанасьев [33-34], Ю.К.Балашов [35] және т.б. ғалымдардың жұмыстарында баяндалады.
Ал А.Г.Цыпкин [36], А.Д.Кутасов [37], И.Ф.Шарыгин [38-39], М.К.Потапов [40-41], В.С.Крамор [42], Б.Г.Авербух [43], К.И.Шахно[44], А.В.Норин[45], П.И.Алтынов[46], Ю.К.Василенко [47], М.И.Нараленков[48] зерттеулерiнде Диофанттық теңдеулерді шешу әдістері қарастырылып, оны практикада қолданудың жолдары анықталған.
Орта мектептегi "Алгебра және анализ бастамалары" курсының ұғымдарын оқыту мәселесi Э.Н.Балаян [49], С.И.Колесникова [50], Е.М.Радионов [51], В.А.Далингер [52-53], Т.А.Алдамуратова [54], А.Қарабаев [55], Е.В.Якушева [56], Д.У.Кенжебеков [57] еңбектерiнде келтiрiлген.
Зерттеудің көкейкестілігі: Анықталмаған теңдеулерді оқыту бағдарламаларын құрастыру әлi күнге толықтай бiр жүйеге келтiрiлмегендiктен, оның ғылыми тұрғыдағы әдiстемелiк нұсқаулары мен тақырыпты оқытуға бағытталған бағдарламалық жабдықтың жеткiлiксiздiгi белгілі мәселе болып табылады.
Осыған байланысты жалпы орта мектептің математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерін зерттеу қажеттігі туындайды. Бұл осы зерттеу жұмысының көкейкестілігін айқындайды.
Жұмыс бар зерттеулерге сүйене отырып, әдістемелік-дидактикалық тұрғыдан негiзделген оқыту және оқушының оқу iс-әрекеттерiн ұйымдастыру жұмыстарын ақыл-ойды сатылап қалыптастыру теориясына сай есеп шығару әдістемесі негiзiнде ұсынылып отыр.
Математиканы оқыту үдерісіндегі оқу материалының күрделілігі, ақпарат көлемінің ауқымдылығы мен уақыттың шектеулілігі оқушылардың оқу материалын толыққанды ұғынуы үшін оқушының мүмкіндіктерінің толық айқындалмауы арасындағы қарама-қайшылықтар осы зерттеу жұмысының өзектілігін көрсетеді.
Сондықтан жұмыстың көкейкестілігі жалпы орта мектептің алгебра және анализ бастамалары (математика) пәнінен анықталмаған теңдеулерді шешу тақырыптарын оқытуда оның әдістемесін және ғылыми негізделген теориясын жасау, пәнді оқыту барысында, оқушылардың пәнге деген қызығушылығын және олардың білім сапасы деңгейін арттыруды анықтауда болып табылады.
Осы аталған зерттеу жұмысының көкейкестілігі, ғылыми - тәжірибелік мәнділігі, жалпы орта мектеп математика пәнін оқыту ерекшеліктері диссертациялық жұмыстың ұсынылып отырған тақырыбын таңдап алуға негіз болды.
Зерттеудің мақсаты: - Жалпы орта мектептің математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерін теориялық негіздеу және олардың шешу жолдарын қарастырып, есептер топтамасын жинақтау.
Зерттеу нысаны: Жалпы орта мектеп математика пәнін оқыту үдерісі.
Зерттеу пәні: Жалпы орта мектептің математика пәнінің тақырыптарын оқытудың мазмұнын, әдістері мен формаларын анықтау.
Жалпы орта мектептің математика пәнінің анықталмаған теңдеулерді оқытуда, есепті шығарудың тиімді әдістерін іздеу диссертациялық жұмыстың зерттеу проблемасы болып табылады.
Зерттеудің ғылыми болжамы: Жалпы орта мектептің математика пәнін оқыту үдерісінде, таңдау курстарда анықталмаған теңдеулерді шешу әдістерін оқушылар толыққанды меңгеріп отырса, онда математика пәнін оқытудың негізгі мақсаттарына қол жеткізіледі, өйткені математиканы оқытуда білім сапасын арттыру үдерісіне сәйкес келеді.
Зерттеудің болжамына қол жеткізу үшін төмендегідей міндеттерді шешу қажет болды:
- Математиканы оқытуда анықталмаған теңдеулерді шешудің теориялық негіздемесін жасау;
- анықталмаған теңдеулерді шешу әдістерін және оның компоненттік құрылымын айқындау;
- Математика пәнін оқытуда анықталмаған теңдеулерді шешуде қолданылатын әдістердің түрлерін негіздеу;
- Оқушыларға анықталмаған теңдеулерді шешу әдістерін үйретуде психологиялық-педагогикалық аспектілерін анықтау және әдістемесін жасау.
Осы міндеттерді шешуде қолданылған жалпы зерттеу әдістері: анықталмаған теңдеулердің тарихи үдерісте қалыптасуын талдау; ғылыми танымдық; оны мектеп практикасына енгізу жолдарын қарастыру; жалпы орта мектеп математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерін, әдістемелік, дидактикалық, педагогикалық және арнайы әдістемелік құралдарды, оқулықтарды, бағдарламаларды теориялық жағынан талдау; математиканы оқытуда анықталмаған теңдеулерді шешу әдістеріне арналған отандық және шетелдік тәжірибелерді зерттеу мен жалпылау, арнайы оқу бағдарламаларын талдау, мектеп мұғалімдері мен оқушылары, әдіскерлермен әңгімелесу; оқыту үдерісін бақылау.
Зерттеудің жетекші идеясы: Жалпы орта мектептің математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерін, пәндік білім, білік және дағдыларын жетік меңгеруге әсерін тигізумен оқыту сапасын арттырады.
Қорғауға ұсынылатын қағидалар:
- Ғылыми-теориялық зерттеулерге талдау жүргізе отырып жалпы орта мектеп математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерінің теориялық негізі жасалды;
- математика пәнін оқытуда анықталмаған теңдеулерді шешу әдіс-тәсілдері айқындалды;
- математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістемесі жасалды.
Зерттеудің ғылыми жаңалығы:
oo Жалпы орта мектептің математика пәнін оқытуда анықталмаған теңдеулерді шешуді қолдануға талдау жасалғанда, қолданудың тиімділігін көрсетеді;
oo математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістемесі анықталады;
oo математика пәнін оқытуда анықталмаған теңдеулерді шешу әдістерін қолданғанда оқушылардың біліктілік деңгейі артады.
Зерттеу жұмысының құрылымы: Зерттеу жұмысы кіріспеден, екі бөлімнен, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.

1 АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫҢ ТҮРЛЕРІ

1.1 Дәрежелік теңдеулер және оларды шешу әдістері

а,в,с, (а= 0) нақты сандар болғанда
а х2 +вх+с =0 (1)
түріндегі теңдеу квадраттық теңдеу деп аталады. Егер а=1 болса, онда квадраттық теңдеу келтірілген , ал егер а!=1 болса, онда келтірілмеген деп аталады. а,в,с сандарының атаулары мынадай: а- бірінші коэффициент, в-екінші коэффициент, с- бос мүше.
а х2 +вх+с =0 теңдеуінің түбірлері
х=
Формуласы боиынша табылады. D=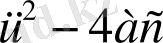өрнегі (1) квадраттық теңдеулердің дискриминанты деп аталады. Егер D0 болса, онда (1) квадраттық теңдеулердің нақты түбірлері жоқ; егер D=0 болса, онда-бір нақты түбірі бар, егер D0 болса, онда-екі нақты түбірі бар болады. D=0 болған жағдайда, кейде квадраттық теңдеулердің бірдей екі түбірі бар дейді. . D= 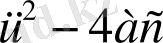белгіленуін пайдаланып, (2) формуласын х= 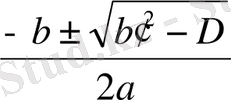түрінде жазуға болады. Егер b=2k болса, онда (2) формуласы
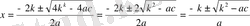түрінде болады . Сөйтіп ,

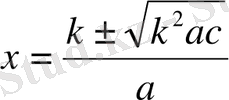
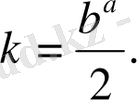
(3) формуласы әсіресе 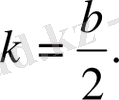бүтін сан, яғни b коэнффициенті жұп сан болғанда қолдануға қолайлы.
Мысал-1 х2+4х+3 =0 теңдеуін шешейік. [1]
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х2+х+3х+3 =х(х+1)+3 (х+1) =(х+1)(х+3)
Демек, теңдеуді былай жазуға болады: (х+1)(х+3) =0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х=-1 және 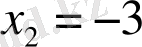сандары х2+4х+3=0 теңдеуінің түбірлері болып табылады.

Мысал-2 : х2+8х-9=0 теңдеуін шешейік.[1]
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х2+8х өрнегін төмендегідей жазып аламыз: х2 + 8х=х2+2х4
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 4-тің екі еселігі. Толық квадрат алу үшін 42-ын қосу керек. Сонда х[2]+2х4+4[2]=(х+4)2
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 42-ын қосып және алып тастаймыз. Сонда шығатыны:
х2+8х-9=х2+2х4+4[2]-9-4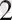=(х+4)2-25
Сонымен, берілген теңдеуді былайша жазуға болады:
(х+4)2-25=0 , яғни (х+4)2=25.
Бұдан х+4=5, х=1 немесе х+4=-5, х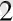= -9.
Жауабы: 1;-9.
Мысал-3
ах2+вх+с=0, а!=0 теңдеудің екі жағын да 4а-ға көбейтеміз, сонда төмендегі өрнекті аламыз:
4а2х2+4ахв+4ас=0
((2ах)2+4ахв+в2)-в2+4ас=0 , (2ах+в)2=в2-4ас
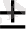
2ах+в= 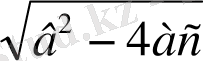, 2ах = -в
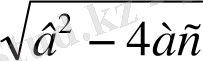
х=.
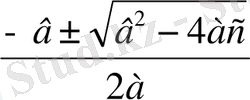Оған төмендегідей мысалдар келтіруге болады:
3х[2]-7х+4=0 теңдеуін шешейік. [2]
а=3, в=-7, с=4. Д=в2-4ас=(-7)2-4·4·3=49-48=1.
Д0 болғандықтан, әр түрлі екі түбірі болады: х1=1, х2=.
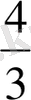Сонымен, дискриминант оң болғанда, яғни в2-4ас0, ах2+вх+с=0 теңдеуінің екі түбірі болады.
Мысал -4 9х2+6х+1=0 теңдеуін шешейік.[2]
а=9, в=6, с=1. Д=в2-4ас=62-4·9·1=0.
Д=0 болғандықтан, бір ғана түбірі бар болады:
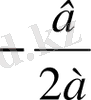х=, х=
Сонымен, егер дискриминант нөлге тең болса, яғни в2-4ас=0, ах2+вх+с=0 теңдеуінің жалғыз түбірі бар болады х=.
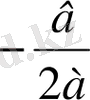Мысал-5 х2+2х+3=0 теңдеуін шешейік.
а=1, в=2, с=3. Д=в2-4ас=4-4·3·1= -8.
Д0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды.
Сонымен, егер дискриминант теріс болса, яғни в2-4ас0, онда ах2+вх+с=0 теңдеуінің түбірі болмайды.
4-әдіс: Виет теоремасын пайдаланып теңдеулерді шешу.
Келтірілген түбірлер Виет теоремасын қанағаттандырады. [3]
Ол былай жазылады: а=1 болғанда, 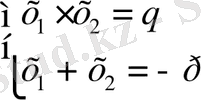(1)
Бұдан келесі тұжырымдарды айтуға болады:
а) Егер (1) теңдеудің бос мүшесі q оң болса (q0), онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р0, онда екі түбірі де теріс болады, егер р0, онда түбірлері оң болады.
Мысал, 1) х2-9х+20=0, х1=4, х2=5, мұнда q=20 0, р=-9 0; [3]
2) х2+5х+6 =0, х1 =-2, х2 =-3, мұнда q =6 0, р =5 0.
б) Егер (1) теңдеудің бос мүшесі q теріс болса (q 0), онда теңдеудің екі түрлі таңбалы екі түбірі болады. Түбірдің модулі үлкені оң болады.
Мысал, 1) х[2]+3х-4 =0; х1 =-4, х2 =1 мұнда q =-4 0, р=-3 0
2) х2-7х-8 =0; х1 =8, х2 =-1 мұнда q =-8 0, р =-7 0
Мысал-6
ах2+вх+с =0 , а !=0 квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз: а2х2+авх+ас=0. ах =у деп белгілесек, х = . Олай болса у2+ву+ас=0 теңдеуіне келеміз. Бұл бастапқы теңдеумен теңбе-тең. Теңдеудің түбірлерін у1, у2 - ні Виет теоремасы арқылы табамыз. Сонда х1 =, х2 = -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті асыра лақтыру әдісі деп атайды. Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
Мысалы, 2х2-9х+9=0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде
у2-9у+18=0 теңдеуін аламыз. Виет теоремасы бойынша
Жауабы: 3; 1,5.
Мысал-7
ах2+вх+с=0, а!=0 квадрат теңдеуі берілген. [4]
Егер а+в+с=0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х1=1, х2=.
Мысалы, 7+2-9=0 қосындысы 0-ге тең. Осы үш сан үшін квадрат теңдеуін жазып, оны шешейік, сонда [3]

1.2 Көрсеткіштік теңдеулер және оларды шешу әдістері

А) Бүтін көрсеткішті дәреже және оның қасиеттері

Натурал көрсеткішті дәреженің анықтамасы бойынша әрбір nN (n1) саны мен а нақты саны үшін
,
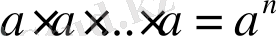және

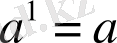
теңдіктері орындалады. Мұнда n саны дәреже көрсеткіші деп, ал а саны негізі деп аталады.
Сонымен бірге әрбір нақты а0 саны мен бүтін теріс m(mZ,m0) саны үшін

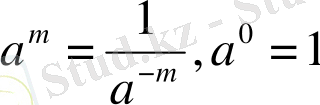
теңдіктері орындалады.
Натурал және бүтін көрсеткішті дәрежелердің қасиеттері ортақ. Атап айтсақ, кез келген а0, b0 нақты сандары мен әрбір бүтін (натурал) n, m сандары үшін төмендегідей теңдіктер орындалады:
1) anam =an+m ; 2) an :am =an-m ; 3) (an )m =anm ; 4) (ab)n =an bn ;
.
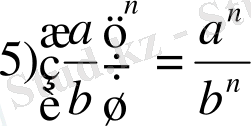Мұнда натурал көрсеткішті дәрежелер негізі а кез келген нақты сан болатынын, ал бүтін көрсеткішті дәрежелер негізі а0 теңсіздігін қанағаттандыратын кез келген нақты сан болатынын ескерсек жөн [36].
М ы с а л.

Ә) Рационал көрсеткішті дәреже және оның қасиеттері

Егер алдында айтылғанда m саны n-ге қалдықсыз бөлінетін болса, онда 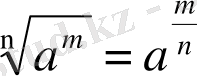теңдігі орындалатынын көрдік. Мысалы, .
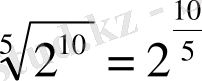Бұл теңдік санның кез келген бөлшек дәрежесін анықтауға мүмкіндік береді.
Анықтама a0 және 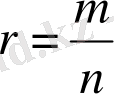рационал саны берілсін. Мұндағы m-бүтін сан, ал n-натурал сан. Онда .
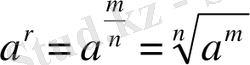Егер r0 және а=0 болса, онда анықтама бойынша 0r=0 деп есептейміз.
М ы с а л ы.

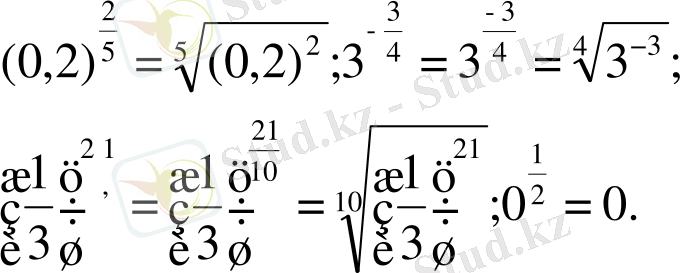
Ал 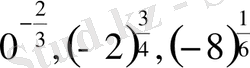сияқты өрнектердің мағынасы болмайды.
Әрбір рационал санды бөлшек сандармен бірнеше түрде өрнектеуге болады. Мысалы, 0,5 саны 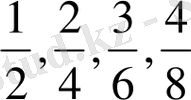т.с.с. сандарына тең. Олай болса, санның r рационал көрсеткішті дәрежесі r санның қандай бөлшек санмен жазылатындығына тәуелсіз болатындығын көрсету керек.
Шынында да, әрбір r рационал санын қыcқармайтын бөлшек түрінде жазуға болады. Айталық, 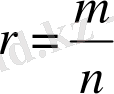қыcқармайтын бөлшек болсын. Онда r-дің басқа бөлшек түрінде жазылуларын 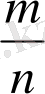бөлшегінің алымын да, бөлімін де бірдей k натурал санына көбейту арқылы аламыз. Сонда біз 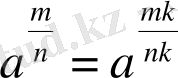теңдігін дәлелдесек, жеткілікті :

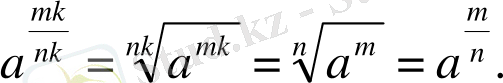
Дәлелдеу керегі де осы.
Санның бүтін көрсеткішті дәрежелерінің негізгі қасиеттері оның рационал көрсеткішті дәрежелері үшін де орындалады.
Егер a0, b0 болса, онда кез келген p және q рационал сандары үшін [37,43].
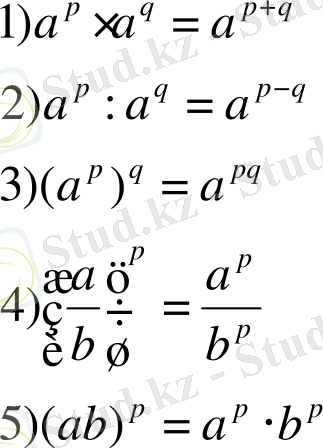
Дәлелдеу. Берілген p және q рационал сандарын бөлімдері бірдей бөлшектермен жазалық: 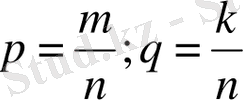. Онда
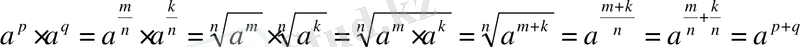Осыдан әрбір рационал p саны үшін

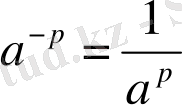
теңдігі шығады. Шынында да, 1-қасиет бойынша аp∙a-p=a0=1. Осыдан 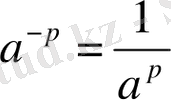болатыны шығады. ap-q∙aq=ap-q+q=ap теңдігінен 2-қасиеттің орындалатындығы шығады.
3-қасиеттің дәлелдеуі: а0, 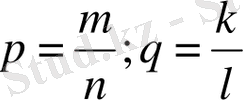болсын. Онда

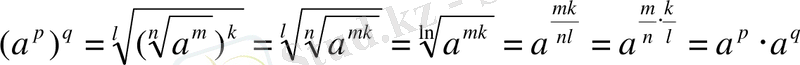
4, 5-қасиеттерінің дәлелдеуі: 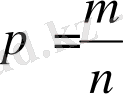болса, онда

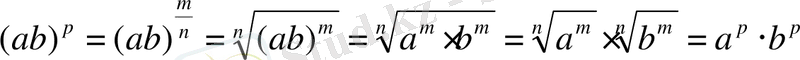
Егер а0, a!=1 және b0 болса, онда ах=b теңдеуін қарапайым көрсеткіштік теңдеу деп атайды. Егер b0 болса, онда бір түбірі бар екені, ал b=0 болғанда оның түбірлері болмайтыны белгілі. Осы мәліметтер бойынша b0 жағдайында ax =b теңдеуінің жалғыз түбірі бар:
x=logab
теңдігімен анықталатындығы шығады.
Әдетте көрсеткіштік теңдеулерді
af(x)=ag(x) (a0, a!=1)
түріне келтіріп шешеді. Бұл теңдеу y=f(x) және y=g(x) функцияларының ортақ анықталу облысында f(x)=g(x) теңдеуімен мәндес болады.
Сонымен көрсеткіштік теңдеулерді мектеп курсында 3-типке бөлген жөн.
* Қарапaйым көрсеткіштік теңдеулерді шешу.
Оның жалпы түрі ах=b мұндағы а0 және a!=1 мұнда y=ax функциясының анықталу облысы барлық нақты сандар, ал мәндерінің облысы оң нақты сандар жиыны екенін ескеру әрбір теңдеу үшін қажет. Өйткені b=0 теңдеуінің түбірі болмайды.
Бұл теңдеуді шешу жолы, ах=b мұндағы b-ны b=ac түрінде өрнектейміз. Сонда теңдеу ax=ac түрге келеді, бұл теңдеудің x=c екені шығады.
Мысалы: 3x-3=81 теңдеуін шешейік.
Ең алдымен 810 шартын ескереміз, бұл шарт орындалады 81=34, 3x-3=34,
x-3=4 бұдан теңдеудің түбірі x=7 екені шығады.
* Квадрат теңдеулерге келтірілетін көрсеткіштік теңдеулерді шешу.
Мұндай теңдеулердің жалпы түрін ka2x+bax+c=0 түрде көрсетуге болады. Бұл түрдегі теңдеулерді шешу үшін ах=у ауыстыру жасаймыз, сонда бастапқы теңдеу ky2+by+c=0 квадрат теңдеуге келеді. Оның түбірлері бар болса, онда олардың көрсеткіштік функция мәндерінің облысында жату шарты тексеріледі, әрі қарай теңдеуді шешу 1-типтегідей жалғасады.
М ы с а л ы: 4x-5*2x+4=0 теңдеуін шешейік.
Теңдеуді 22x-5*2x+4=0 түрде жазып 2x=y алмастыру жасасақ, онда теңдеу
y2-5y+4=0 түрге келіп, оның у=4 және y=1 екі шешімі болады. Бұл екі сан үшін 40 және 10 шарттары орындалады. Сондықтан алмастыру теңдеуін 2x=4 және 2x=1 шешсек x=2, x=0 шығады.
* Негіздері әр түрлі болып келген көрсеткіштік теңдеулерді шешу.
Мектеп курсындағы мұндай теңдеулердің тек дәрежелері бірдей болып келгенде ғана оларды шешуге қол жетеді. Оны мысал арқылы шығару жеткілікті, мұнда негізінен дәреженің негізгі қасиеттерін кеңінен қолдану керек.
М ы с а л ы. 5x+2=8x+2 теңдеуін шешейік. 8x+20 болғандықтан, 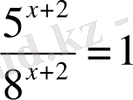етіп түрлендіреміз, одан 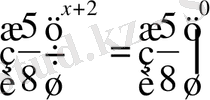шығады. Сонда х+2=0-ден х=-2 түбірі табылады.
Осылай көрсеткіштік теңдеулерді типке бөліп, оларды шығару жолдарын қарастырғаннан кейін көрсеткіштік теңсіздіктерді және теңдеулер жүйесін шешуде біршама жеңілдіктер тудырады. Басқа да тақырыптарды осылай типтерге бөліп түсіндіру оқушыларға әрі түсінікті , әрі қабылдауына жеңіл. Сыныптағы оқушылардың білім деңгейіне қарай берілетін есептердің қиындығын өзгертуге болады [40].

1-м ы с а л. 4x + 2 + 2 :: 4x - 5x + 2 = 5 :: 5x.
Қосылғыштардың орнын ауыстырып, теңдеуді мынандай түрде жазайық: 4x + 2 + 2 :: 4x = 5x + 2 + 5 :: 5x, бұдан шығатыны 4x (16 + 2) = 5x (25+5) = 18 :: 4x = 30 :: 5x

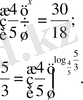
Жауабы x=
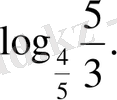
2-м ы с а л. 2[х] + 4 :: 3[х] = 576.
Сол жақты өрнектеп алайық : 16 :: (2[х] :: 3[х]) = 576 теңдеудің екі шетінде 16-ға бөлейік:
6х = 36;
х = 2.
Жауабы 2.
3-м ы с а л.
Теңдеуді мынадай түрде жазайық: жаңа айнымалы енгізейік t = 2x (t 0). Сонда қарапайым квадрат теңдеу аламыз.
2t2 + 16t - 40 = 0, = t2 + 8t - 20 = 0, оның шешімдері t1 = 2, t2 = - 10 0 - бөтен түбір. t орнына 2 қоямыз: 2х = 2, х = 1.
Жауабы 1.
4-м ы с а л.
Егер теңдеудің сол жағын былай жазсақ: дәреженің негізінің ( 4, 10, 25 сандары) геометриялық прогрессияны құрайтынын байқауға болады. Мұндай жағдайда екі жағында 25x-ке бөлсек ( себебі x-тің ешқандай мәнінде бұл өрнек 0-ге тең емес), мынадай теңдеу алуға болады немесе
Жаңа айнымалы енгізейік осыдан шығатыны t2 + 2t - 8 = 0, оның шешімдері t1 = 2, t2 = - 4 0 - бөтен түбір. t орнына 2 қоямыз:
Жауабы .
5-м ы с а л. 12x :: 4x - 5x :: 2x + 1 - 9 :: 4x + 1 + 30 :: 2x = 0.
Теңдеудің сол жағын көбейткіштерге жіктейік: Бірінші көбейткіш ешқашан 0-ге тең емес. Сондықтан мына теңдеулердің түбірлері берілген есептің шешімі болады:
А) 2х - 6 = 0, х = 3.
Б)

Жауабы 3;
а) Қарапайым көрсеткіштік теңдеулер [42,48].

ә) Квадрат теңдеулерге келтірілетін көрсеткіштік теңдеулер:

б) Негіздері әр түрлі болып келген көрсеткіштік теңдеулер:

в) Негіздері геометриялық прогрессияны құрайтын көрсеткіштік теңдеулер:
г) Теңдеудің екі жағын да логарифмдеу арқылы шешілетін көрсеткіштік теңдеу:

Шешулері а)

Жауабы 3.

Жауабы 3.

х=4
Жауабы 4.
ә)

айнымалы енгізейік

Жауабы 0.

айнымалы енгізейік ;

Жауабы 1.

айнымалы енгізейік

Жауабы 0,

айнымалы енгізейік

Жауабы: 1;3.

айнымалы енгізейік

Жауабы: 3

Жауабы: 0;1;2.

Жауабы: -3.

Жауабы:
в)
16, 36,81 сандары геометриялық прогрессияны құрайды.
Сол себепті біз теңдеуді 81x-не бөлеміз:

Жаңа айнымалы енгізейік

Жауабы: 0; .

4, 6, 9 сандары геометриялық прогрессияны құрайды.
Сол себепті біз теңдеуді -не бөлеміз:

Жаңа айнымалы енгізейік

Жауабы: -2

4, 6, 9 сандары геометриялық прогрессияны құрайды.
Сондықтан біз теңдеуді -не бөлеміз:
Жаңа айнымалы енгізейік

Жауабы: 0.
г)

Теңдеудің екі жағында логарифмдейік (негізі 10):

Жауабы: 0; .

Көрсеткіштік теңдеулер жүйесін шешу

Көрсеткіштік теңдеулер жүйесін шешуді қарастырайық.
Анықтама. Құрамында көрсеткіштік теңдеуі бар теңдеулер жүйесін көрсеткіштік теңдеулер жүйесі деп атаймыз.
Көрсеткіштік теңдеулер жүйесін шешу үшін көрсеткіштік функцияның қасиеттері, көрсеткіштік теңдеулер және теңдеулер жүйесін шешудің тәсілдері қолданылады.
Осыған мысалдар қарастырайық.
1 - мысал. теңдеулер жүйесін шешейік.
Шешуі. Берілген теңдеулер жүйесін шешу үшін алмастыру тәсілін қолданып, мәндес теңдеулер жүйесін аламыз:

Осыдан немесе теңдеуі шығады, бұдан аламыз. Енді деп алып, квадрат теңдеуін шешеміз. Шыққан квадрат теңдеудің түбірлері Сонда Демек, онда сәйкесінше
Жауабы:

2 - мысал. теңдеулер жүйесін шешейік.
Шешуі. Теңдеулер жүйесінде екі көрсеткіштік функция берілген. Алдымен жаңа айнымалылар енгізейік, яғни сонда екі белгісізі бар сызықтық теңдеулер жүйесін аламыз: .
Алгебралық қосу тәсілі бойынша соңғы теңдеулер жүйесінің екінші теңдеуін 2 - ге көбейтеміз: . Бұдан немесе аламыз. - дың мәнін жүйенің бірінші теңдеуіне қойсақ, аламыз.
Сонда көрсеткіштік теңдеулері шығады. Оларды шешіп, аламыз.
Жауабы:

3 - мысал. теңдеулер жүйесін шешейік.
Шешуі. Жүйенің екінші теңдеуінен табатынымыз: 2x-y=1, бұдан y=2x-1. Бірінші теңдеудегі у-тің орнына 2х-1 өрнегін қойып, табатынымыз +. - ін t арқылы белгілеп, мынадай квадрат теңдеуге келеміз , бұдан және . Алмастырудың теңдеуінің шешімі болмайды. Ал теңдеуінің түбірі х=2 саны. у-тің сәйкес мәні 3-ке тең.
Жауабы:

4 - мысал. теңдеулер жүйесін шешейік.
Шешуі. Берілген көрсеткіштік теңдеулер жүйесін шешу үшін, бірінші көрсеткіштік теңдеуді екінші көрсеткіштік теңдеуге бөлеміз. Одан алатынымыз

x-ті өрнектеп алғаннан соң, бастапқы кез-келген көрсеткіштік теңдеуге қоямыз.

.
Сәйкесінше болады.
Жауабы: (1;2)

5 - мысал. теңдеулер жүйесін шешейік.
Шешуі. Берілген көрсеткіштік теңдеулер жүйесін шешу үшін, екінші теңдеуден х-ті өрнектеп аламыз. Сөйтіп бірінші теңдеуге қойып шешеміз:

Бұл теңдеуді қарапайым көрсеткіштік теңдеу сияқты шешеміз.

Енді х-терді анықтаймыз =36+2=38 және .
Жауабы: (38;-6), (3;1)

1.3 Логарифмдік теңдеулер және оларды шешу әдістері
Логаритімдік теңдеулер. Қарапайым логарифмдік теңдеу ) түрінде болады. теңдеуін шешу үшін : 1) теңдеуі үшін бөгде түбірлер болады.
Логарифммдік теңдеулерді шешудің негізгі екі әдісі бар: 1) берілген теңдеуді түрінде түрлендіру , содан кейін оны түрінде түрлендіру әдісі; 2) жаңа айнымалы енгізу әдісі .
1-мысал теңдеуін шешу керек.
Шешу. Берілген теңдеуден теңдеуіне көшеміз де оны шешеміз. Сонда бұдан х -*тің табылған мәндерін тексксеруді және теңсіздіктері арқылы орындаймыз. -3 сан бұл теңсіздіктерді қанағаттандырады . Ендіше 4- бөгде түбір.
Жауап: х=-3
2-мысал. теңдеуін шешут керек.
Шешуі. Логарифмдердің қосындысы қөбейтіндінің логарифміне тең екінін (120- пунктті қараңыз) пайдаланып, теңдеуді
Түрінде түрлендіреміз де одан кейін (х+4)(2х+3һ1-2х ) теңдеуін аламыз. Сонғы теңдеуден Енді тексеру ғана қалды. Оны х+406 2x+306 14-2x0 теңсіздіктерінің системасы арқылы орындауға болады. Табылған -1 мен -5,5 мәндерін осы теңсіздіктерге кезекпен қойып , - теңсіздіктерді қанағаттандыратынына, ал 5,5- бірінші мен екінші теңсіздіктерді қанағаттандымайтынына көз жеткіземіз. Олай болса , -5,5-бөгде түбір.
Жауап: х=-1
3-мысал. теңдеуін шешут керек болғандықтан,ғ берілген теңдеуді былай жазамыз: деп алып, жаңа айымалы енгіземіз. Сонда әрі қарай (у-1)( екенін аламыз. Ал сондықтан теңдеуінен х=4 екенін табамыз .

Жауап: х=4.
153. Көрсеткіштік - логарифмдік теңдеулерді шешудің мысалдары.
1-мысал. Жазу керек

Көрсеткіштік-логарифмдік теңдеулерді шешу жолдары

Мысал-1. теңдеуін қарастырайық [45,46,48].
Ш е ш у і. ММЖ теңсіздігімен анықталады.
Теңдеудің екі жағын да негізін 10 етіп логарифмдесек, онда мынаны аламыз :

Бұл теңдеудің түбірлерін табу үшін, мына екі және теңдеулердің шешімдерін анықтау қажет. және Мәндері және .
Сонымен теңдеудің 3 шешімі бар: .
жауабы: .
Мысал - 2. теңдеуін қарастырайық.
Ш е ш у і. ММЖ теңсіздігімен анықталады. Берілген теңдеуді былайша жазайық. Оны мынадай түрге келтірейік. Теңдеудің екі жағын да негізін 10 етіп логарифмдесек, онда мынаны аламыз :

Бұл теңдеудің түбірлерін табу үшін, мына екі және теңдеулердің шешімдерін анықтау қажет. Бірінші теңдеуден , , ал екіншіден , және үшіншіден , анықтаймыз.
Сонымен теңдеудің 3 шешімі бар: . Жауабы .
Мысал - 3. теңдеуін қарастырайық.
Ш е ш у і. ММЖ теңсіздігімен анықталады. Теңдеуді мына түрде жазып алайық. Теңдеудің екі жағын да негізін 10 етіп логарифмдесек, онда мынаны аламыз :

Бұл теңдеудің түбірлерін табу үшін, мына теңдеулерді және шешейік. Бірінші теңдеуден болады. Ал екінші теңдеуді байланысты квадраттық теңдеуді шешеміз, одан мынадай шешімдер және аламыз.
Сонымен теңдеудің 3 шешімі бар:
жауабы:
Мысал - 4. теңдеуін қарастырайық.
Ш е ш у і. ММЖ теңсіздігімен анықталады. Бұл теңдеуді шешу үшін мына екі жағдайды қарастыру қажет:
1) 2)
Бірінші теңдеуден екі жауап аламыз. , өйткені шартты қанағаттандырмайды, ал қанағаттандырады. Ал жүйеден мынадай теңдік аламыз. Осы теңдеуді байланысты квадраттық теңдеу шешеміз:
, , , х3=1000.
Сонымен теңдеудің 3 шешімі бар:
жауабы:
Мысал - 5. теңдеуін қарастырайық.
Ш е ш у і. ММЖ x0.

Жаңа айнымалы енгізейік, . Мынадай теңдеуді шешейік ,

1) , ;
2) , , ;

Сонымен теңдеудің 3 шешімі бар:
жауабы:

,

2 АНЫҚТАЛМАҒАН ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ.
2.1 Теңдеу және оның бүтін шешімі туралы
Бір белгісізі бар бірінші дәрежелі мынадай теңдеуді қарастыралық
. (1)
Айталық теңдеудің коэффициенттері а1 және а0 бүтін сандар болсын. Бұл теңдеудің шешімі

бүтін сан болады сонда тек сонда, егер а0, а1-ге бүтін сан болып бөлінсе. Сөйтіп, (1) теңдеу барлық уақытта бірдей бүтін шешімге ие бола бермейді; мысалы, мына екі теңдеудің және біріншісі бүтін шешімге , ал екіншісі бүтін шешімге ие емес.
Бұндай жағдаймен дәрежесі бірден жоғары теңдеуде де кездесеміз: квадрат теңдеуі , бүтін шешімдерге ие, ал квадрат теңдеуі бүтін шешімдерге ие емес, себебі , бұл иррационал сандар.
Бүтін коэффициентті п дәрежелі теңдеудің бүтін түбірлері туралы мәселені қарастыралық
(). (2)
Айталық бұл теңдеудің бүтін түбірі болсын, сонда
,
,
немесе
.
Соңғы теңдіктен көрінеді, а0 а-ға қалдықсыз бөлінетіндігі. Сондықтан, (2) теңдеудің әрбір бүтін түбірі теңдеудің бос мүшесінің бөлгіші болып табылады. Теңдеудің бүтін шешімдерін табу үшін а0-дің сондай бөлгіштерін таңдау керек, оларды берілген теңдеуге апарып қойғанда, оны теңбе-теңдікке айналдыратын. Мысалы, 1, - 1, 2 және - 2 сандары мына

теңдеудің бос мүшесінің бөлгіштері болып табылады. Бірақ, олардың ішінде жалғыз бүтін түбірі болады. Дәл осы әдіспен мына теңдеудің

бүтін сандарда шешімі жоқ.
2.2 Бірнеше белгісізі бар теңдеулер
Бірнеше белгісізі бар теңдеулердің бүтін шешімдері туралы мәселе өте маңызды және күрделі.
Екі белгісізі бар бірінші дәрежелі теңдеулер. Екі белгісізі бар бірінші дәрежелі мынадай теңдеуді
(3)
қарастыралық, бұндағы а мен b - нольден өзгеше бүтін сандар, ал с - кез келген бүтін сан.
а және b коэффициенттерінің өзгеше ортақ бөлгіштері жоқ болсын деп есептейміз. Шынында, егер бұл коэффициенттердің бірден өзгеше ең үлкен ортақ бөлгіші болса, онда , теңдіктері әділетті болады. Сонда (3) теңдеу мына түрді қабылдайды:

және бүтін шешімдерге ие болады сонда тек сонда, егер с d-ге бөлінетін болса. Сөйтіп, болған жағдайда (3) теңдеудің барлық коэффициенттері d-ге бүтін сан болып бөлінеді, және (3)-ті d-ге қысқартып, мынадай теңдеуге келеміз
,
бұл теңдеудің коэффициенттері а1 мен b1 өзара жай сандар.
Алдымен болған жағдайды қарастыралық. Онда (3) теңдеу мына түрде жазылады
. (3)
Бұл теңдеуді х-ке қарағанда шешіп, мынаған келеміз
.
Анық, х бүтін мәндерді қабылдайды, онда тек сонда, егер у а-ға қалдықсыз бөлінетін болса. Сонда а-ға еселік болып ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.