Математикалық есеп және оқушының танымдық белсенділігін дамыту

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:

МАТЕМАТИКАЛЫҚ ЕСЕП ЖӘНЕ ОҚУШЫНЫҢ ТАНЫМДЫҚ БЕЛСЕНДІЛІГІН ДАМЫТУ

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3

1 МАТЕМАТИКАЛЫҚ ЕСЕП ЖӘНЕ ОҚУШЫНЫҢ ТАНЫМДЫҚ
БЕЛСЕНДІЛІГІН ДАМЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ ... ... ... ... ... ... .. ... ... 5

1.1 Математикадағы есеп ұғымы және есепті шығаруға талдамалар ... ... 5

1.2 Оқушының танымдық белсенділігі және ондағы математикалық есептің рөлі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 26

2 МАТЕМАТИКАЛЫҚ ЕСЕП ЖӘНЕ ОҚУШЫНЫҢ ТАНЫМДЫҚ
БЕЛСЕНДІЛІГІН ДАМЫТУДЫҢ ЖОЛДАРЫ ... ... ... ... ... ... ... ... ... ... ... ... ... 39

2.1 Ауызша есептеу арқылы оқушының танымдық белсенділігін дамыту ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 39

2.2 Стандарт емес есептерді шығару арқылы оқушыны танымдық белсенділігін дамыту ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 46

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 55

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... 57

КІРІСПЕ

Зерттеу жұмысының көкейкестілігі. Егеменді еліміз тәуелсіз ел болғалы барлық салаларда ауқымды өзгерістер жүріп жатыр. Мұндай өзгерістерден білім саласыда тыс қалған жоқ. Қазіргі білім беру жүйесі әлемдік өркениеттің барлық талабына сай келетін, білім мен біліктілігі жетілген жеке тұлғаны қалыптастыруды қажет етеді.
Қазақстан Республикасы Білім туралы Заңында Білім беру мазмұны жеке адамның жалпы мәдениетін қалыптастыру, жеке адамды қоғамдағы өмірге беуімдеудің міндеттерін шешу, мамандықты саналы түрде таңдау мен меңгеру үшін негіз жасауға бағытталған болуы керек, делінген.
Сондай-ақ Қазақстан Республикасы 12 жылдық жалпы орта білім беру тұжырымдамасында 12 жылдық білім берудің басты мақсаты: өзінің және қоғамның мүддесінде өзін-өзі белсенді етуге дайын, өзгермелі даму үстіндегі ортада өмір сүруге бейім, бәсекеге қабілетті және құзыретті, шығармашыл, білімді тұлғаны дамыту және қалыптастыру деп, атап өткен.
Міне осы мәселелерді ойдағыдай шешуде оқушылардың математиканы оқыту үдерісіндегі мүмкіндіктерді, заман талабына сай түрлендіріп пайдалануға болады. Математика пән ретінде оқушыларға осы пәннің теориялық негіздері мен практикалық іс-әрекеттерін меңгеруге мүмкіндік береді. әсіресі математикалық есептер шығару үдерісінде жаңа инновациялық тәсілдерді тиімді пайдалана отырып оқушылардың шығармашылық белсенділігін арттыруға болады. Математиканы оқыту барысында есеп шығарудың маңызы туралы ғылымдар Ю.К.Бабанский, Б.М.Есипов, И.Я.Лернер, М.Н.Скаткин,А.В.Усова, Б.Баймұханов, т.б. атап өтсе, есеп шығару үдерісінің психологиялық негіздеріне С.Л.Рубинштейн, А.Н.Леонтьев, Н.Ф.Талызина, Я.А.Пономарев, Г.А.Балл т.б. ғылыми талдаулар жасады. Сондай-ақ математикалық есептерді шығарудың тәсілдерін В.М.Брадис, Д.Пойа, Ю.М.Колягин, Н.И.Кондаков, О.Сатыбалдиев, К.Әбдімәжитов, Ш.Омашев, А.Ф.Эсаулов т.б. өз еңбектерінде қарастырған.
Ал, оқушының шығармашылық белсенділігі және оны арттыру мәселелері Н.Лук, Г.С.Альтшуллер, Г.С.Батищев, Д.Б.Богоявленская, П.К.Энгельмейер, И.Пуфаль-Струзик, В.А.Моляко, А.М.Матюшкин,
Ә.Сағымбаев, Т.М.Мажикеев т.б. ғылымдардың еңбектерінде талдаулар жүргізілген.
Математикалық есеп арқылы оқушының танымдық белсенділігін дамыту мәселелерінде әлде де болса шешімін таппаған жағдайлар бар, өйткені казіргі кезде білім берудің педагогикалық жаңа ұстанымдары өмірге енуде. Енді оқушыны оқыту үдерісінде ойлауға үйрету, осы арқылы шығармашыл тұлға қалыптастыру міндеті қойылып отыр. Сондықтан есеп шығарту арқылы оқушыға математикалық білім ғана беру емес, математикалық есеп шығарту арқылы оқушының танымдық белсенділігін дамыту. Міне аталған дипломдық жұмыстың көкейкестілігі де осында.
Дипломдық жұмыстың мақсаты-жалпы орта мектептегі математика сабақтарында есеп шығарту арқылы оқушының танымдық белсенділігін дамытудың әдістемелік жүйесін жасау.
Зерттеп отырылған мәселеге байланысты ғылыми әдебиеттерге талдау жасап және озат мұғалімдердің іс-тәжірбиесіне сүйене отырып мынадай зерттеу болжамын ұсынамыз. Егер математика сабақтарында есеп шығарту барысында түрлі әдіс-тәсілдерде пайдалана отырып, жүйелікпен сабаққа оқушының қызығушылығын, ынтасын, ойлауын туғызсақ, онда олардың танымдық белсенділігі дамиды. Өйткені оқушы қызығушылығы, өзбетінше ізденісі оның танымдық белсенділігінің артуына ықпал етеді.
Зерттеу нысаны- жалпы орта мектептегі математика пәнін оқыту үдерісі.
Зерттеу пәні- жалпы орта мектептегі математиканы оқыту кезінде есептерді пайдалану әдістемесі.
Зерттеудің ғылыми - әдістемелік міндеттері:
oo математикадағы есеп ұғымының мәнін ашу;
oo танымдық , танымдық белсенділіктің ғылыми негіздеріне талдау жасау;
oo математикалық есептерді шығару тәсілдеріне талдаулар жүргізу;
oo түрлі математикалық есептерді шығару кезінде оқушының танымдық белсенділігін дамыту тәсілдерін көрсету.
Бұл міндеттерді шешу үшін мына төмендегідей әдістер қолданылды:
oo зерттеу тақырыбы бойынша психологиялық-педагогикалық және әдістемелік әдебиеттермен танысып, оларға ғылыми-әдістемелік тұрғыдан талдау жасалды;
oo зерттеу бойынша мектептегі математика пәні мұғалімдерінің озық іс-тәжірибелерімен танысылды;
oo мектеп оқушыларымен ұжымдық түрде әңгіме өткізіліп, сауалнамалар жүргізілді оларға талдаулар жүргізілді.
Зерттеудің ғылыми жаңалығы:
- математикалық есеп ұғымының гнесологиялық мәнінің ашылуы;
- оқушының танымдық белсенділігін дамытуда есеп шығарудың
мүмкіндіктері анықталды;
Қорғауға мынадай қағидалар ұсынылады:
- жалпы орта мектеп математикасындағы есеп ұғымы мен есепті
шығарудың теориялық және әдістемелік негіздері;
- есеп шығарту үдерісінде оқушының танымдық белсенділігін
дамыту мүмкіндіктерін көрсету;
Диплом жұмысының құрылымы: Диплом жұмысы кіріспеден, екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.

1 МАТЕМАТИКАЛЫҚ ЕСЕП ЖӘНЕ ОҚУШЫНЫҢ ТАНЫМДЫҚ
БЕЛСЕНДІЛІГІН ДАМЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

1.1 Математикадағы есеп ұғымы және есепті шығаруға талдамалар

Еліміздің әлеуметтік-экономикалық дамуының стратегиялық бағыттарына сәйкес білім беру жүйесін дамыта отырып, әлемдік білім кеңістігіне ықпалдастырудағы негізгі бағдар - адамды қоғамның ең маңызды құндылығы ретінде танып, оның рухани жан-дүниесінің дамуына, көзқарастары мен танымдық әлеуетінің міндеттерді жүзеге асыру еліміздегі мектептерде оқыту үдерісінің мазмұндық болмысын жаңа әдіснамалық тұрғыдан негіздеуді талап етеді. Мұндай жаңа әдіснамалық жүйе дәстүрлі оқыту үдерісінің түбегейлі өзгертудің қажеттігін көрсетеді. [1]
Осыған орай жалпы білім беру мектептеріндегі пәндерді жаңаша оқыту қажеттілігі туып отыр. Оның ішінде математиканың маңызы зор.
Мұнда ғылыми танымда және дүниені түрлендіруде "есеп" ұғымының мәнін анықтау қажетті және өзекті мәселелердің бірі болып табылады. Аталған ұғымды пара-пар түрде талдаудың маңызды шарты қазіргі гносеологиялық ахуалдың ерекшеліктерін бүтіндей ескеру болып отыр. Бұл ерекшеліктер ғылыми танымның ерекше категориялық және методологиялық деңгейлерін қалыптастыру кезінде өз көріністерін табады.
Математика ғылым ретінде есептен пайда болған және есеп арқылы дамиды. Мектеп математикасын есепсіз құру мүмкін емес.
Ресейдегі алғашқы Арифметика оқулығының авторы Л.Ф.Магницкий арифметикалық төрт амалды қолдануға арналған есептер жүйесін құрастырған.
Математикалық есеп оқушылардың ұғымдарды, теорияны және математика әдістерін меңгерудің тиімді де, айырбасталмайтын құралы болып табылады. Оқушылардың ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктері мен дағдыларының қалыптасуында, математиканың практикамен байланысын көрсетуде есептің алатын орны зор.
Оқу есебін және оны шығаруды оқытудың нәтижелеріне жетудің құралы ретінде айқындайтын және қарастыратын орыс дидактары (Ю.К.Бабанский[2], Б.П.Есипов[3], И.Я.Лернер[4], М.Н.Скаткин[5], А.В.Усова[6]) есептерді оқытуда пайдаланудың теориясы мен практикасын дамытуда үлкен үлес қосты.
Оқушылардың математикалық білімдерді терең және берік меңгерулері, өзінің жүру барысында оқушылар бойында жаңа білімдер, біліктер мен дағдылар қалыптасатын, математикалық алғы шарттар пайда болатын, математикалық әдебиеттермен өз бетінше жұмыс істей алу дағдылары қалыптасатын оқу қызметін ұйымдастыруды қажет етеді. Бұған көп жағдайларда оқушылардың бойында негізгі математикалық білімдер, біліктіліктер мен дағдылар жүйесін қалыптастырудың, олардың математикалық дамуының маңызды құралы және олардың оқу қызметінің жетекші нысаны болып табылатын-есептерді тиімді пайдалану мүмкіндік тудырады.
Оқушыларды есептерді шығаруға үйрету педагогика ғылымының ең маңызды да күрделі мәселелерінің бірі болып табылады. Бұл мәселені зерттеуге Я.И.Груднов., Л.Л.Гурова., В.А.Гусев., Г.В.Дорофеев., В.А.Жаров., Л.М.Фридман., Р.С.Черкасов., А.Ф.Эсаулов және тағы басқалардың еңбектері арналған. Бұл зерттеулерде математикадан есептік материалдарды жетілдіруге сөзсіз мүмкіндік тудыратын, есептерді сұрыптау мен жүйелеуге, оларды шығарудың әдістерін көрсетуге ерекше көңіл бөлінеді.
Алайда, математиканы оқыту үдерісінде математикалық оқу есептерін пайдалануға арналған зерттеулердің көптігіне қарамастан, бұл мәселе әлі де өзінің толық шешімін талап етуде.
"Есеп" ұғымының мәнін, рөлін және орнын, оны дұрыс қалыптастырудың дидактикалық функциялары мен шарттарын философиялық, жалпы ғылыми және нақты ғылыми тұрғыдан қарастыру қажет. Бөлініп көрсетілген аспектілердің диалектикалық бірлікте және әрекеттестікте жүзеге асырылуы "есеп" ұғымына талдау жасаудың жүйелі тәсілінің мазмұнын құрайды.
Америкалық ғалым Д.Пойаның "есеп" ұғымын түсінуі де қызық. Ол "есеп анық көрінетін, бірақ тікелей жақындауға болмайтын мақсатқа жету үшін, оған сәйкес келетін құралдарды саналы түрде пайдалануды қажет етеді" деп көрсетеді.[7] Осы жағдайда аталған ұғымның мазмұнын біржақты қарастыру ісімен байланысты боламыз.
А.Ф.Эсаулов бойынша есеп мазмұнының түйіні проблема болып табылады, яғни "есеп-бұл негізінде проблема жаткан қандай да бір талдаудың жемісі"[8]. Ғалымның жоғарыда айтқан позициясы есеп анықтамасының мазмұнын біршама тарылтады және бір жағынан алғанда оны проблемалық ахуалға әкеледі.
Біздің көзқарасымыз бойынша, есеп ұғымы туралы Г.А.Балл берген түсінік терең мағынаға ие болады. Есепті субъектінің қызметіне және оның қызметінің әрбір шарттарына қойылатын талаптар ретінде қарастыра отырып, ол, есеп ұғымын үш негізгі аспектілер бойынша анықтау қажеттігін атап көрсетеді.
Біріншіден (А.Н.Льеонтев бойынша), іс-әрекеттің мақсаты ретінде.
Екіншіден (Г.С.Костюк бойынша), белгісіздің белгілімен байланысы негізінде белгісізді табуға бағытталған, субъектіден кейбір әрекетті жүзеге асыруды талап ететін ахуал ретінде.
Үшіншіден (А.Ньюэлл бойынша), субъект әрекеттерді жүзеге асыру әдістеріне ие бола алмайтын шарттар жағдайында, белгісіздің белгілімен байланысы негізінде белгісізді табуға бағытталған, сол субъектіден кейбір әрекетті жүзеге асыруды талап ететін ахуал ретінде.
Есепке қатысты осындай көп аспектілі тәсілді қолдану есептердің келесі үш түріне айқындап көрсетуге негіз болады. Олар: есептер, ойлану есептері, проблемалық есептер. Осы айтылғандардан, аталған ұғымдардың бір-біріне бағыныштылығын көреміз, оларда іс-әрекет мақсаты субъектінің тәжірибесі және оның есепті шығару тәсіліне ие екендігі есепке алынады.
Осындай көзқарас тұрғысынан қарағанда есеп-мақсат, тапсырма, мәселе, проблема, оқыту және бақылау әдістерінің бірі болып табылады.
"Есеп" ұғымын дидактиканың жалпы және жеке бөліктеріне сай талдай отырып, біз негізгі назарды оқу есептеріне аударамыз. Оқу есептері өзінің құрылымы мен атқаратын міндеті бойынша жалпы есеп ұғымынан айырмашылығы бар. Оқу есептері оқу қызметінің элементі болып табылады. В.В.Давыдов оқу есептері заттық шындықтың мейлінше жалпы қатынастарын игеруге бағытталған ақыл-ой қызметінің белгілі бір тәсілдерін талап ететіндігін атап көрсетеді [9]. Оқу есептері ғылыми және практикалық салалардағы проблемалардың салыстырмалы түрдегі кең ауқымды бөліктерін шешудің жалпы әдістерін ашуды және игеріп алуды қажет етеді. В.В.Давыдов бойынша, "өзінің қойылу сәтінен оқу қызметі басталатын оку есебі, оқушының теориялық ұғымдардың пайда болу шарттарын талдауға және меңгерілуге тиісті пән аймағының кейбір жалпы қатынастарға бағдарланған сәйкес әрекеттердің жинақталған тәсілдерін игеруге бағытталған. Басқаша айтқанда, оқу есебінің елеулі мінездемесі, оқушылардың нақты-тәжірибелік есептердің кейбір топтарын шығарудың мазмұнды жинақталған әдістерін меңгерулеріне қызмет етеді".
Дидактикалық әдебиетте есеп түсінігінің бірқатар анықтамалары бар. Оларды екі топқа бөлуге болады: С.Л.Рубинштейннің, А.Н.Леонтьевтің, Г.А.Баллдың, Я.А.Понамаревтің психологиялық анықтамалары және Л.М.Фридманның, И.Я.Лернердің, В.И.Крупичтің дидактикалық анықтамалары.
С.Л.Рубинштейн 40-шы жылдардың өзінде Шарттармен көрсетілген мақсат есепті (міндетті) анықтайды, ал ол басқа іс-қимылдармен шешіледі деп жазды. Адамның әрбір саналы іс-әрекеті мәселе (есеп) шешу болып табылады. Рубинштейн пікірі бойынша, субъектінің мәселеге қатынасы іс - қимылдардың ішкі мағынасын құрайды. Осы қатынастың арқасында мәселе түсініленді және қабылданады. Рубинштейн еңбектерінде мәселе түсінігі ең алдымен тілдік қалыптармен байланысты болып келеді, осы үдерісінде ол адамның субъективті игілігіне айналады. әрбір мәселе-есепте толтыруға тиесілі толмаған бос орындар секілді белгісіздер бар. Осындай жағдайда субъект есепті (мәселені) шешу үшін жаңа білімдерді меңгеріп, қажетті ақпараттарды тауып отыруы тиіс. Мәселеде болатын қарама-қайшылықтар ойлау үдерісін қажеттілікпен тудырады.Сөйтіп, мәселе-есеп ұғымын талдаған уақытта С.Л.Рубинштейн ішкі мен сыртқының бірлігінен бастау алады. [10]
Мәселе ұғымына классикалық-психологиялық анықтаманы А.Н.Леонтьев береді.[11] Ол мәселе-белгілі бір жағдайларда анықтамасы қажеттілік, себептілік деген мағынасы категориялармен толықтырылады. Мәселені талдай отырып ол оны қимыл-қозғалыспен емес, жалпы іс-әрекетпен байланыстырады. Адам іс-әрекетінде А.Н.Леонтьев қимыл-қозғалыс пен операцияларды анық ажыратады, оның алғашқылары мақсатқа, ал қалғандары-аталмыш мақсатқа жету шарттарына жатады. [12]
Н.Ф.Талызина адамның мәселені шешу үдерісін оқып біліп, былай дейді: Әрекет-бір себеп және мақсатпен біріккен қимыл-қозғалыстар мен мақсаттар жүйесі.
Мәселе ұғымының анықтамасы Я.А.Понамаревтің еңбектерінде де беріледі.Оның пайымдауында мәселе ол іс-қимылын анықтайтын жағдай, ол сол жағдайды өзгерте отырып қажеттілігін қанағаттандырады. [13] Мұндағы мәселе жағдай ұғымымен анықталады. Я.А.Понамаревтің кейбір ізбасарлары мәселе ұғымымен не жағдай немесе жүйе категорияларымен анықтайды. Мысалға, Г.А.Балл мәселені субъект әрекет етуге тиісті қандай да жағдай деп қарастырады.
Мәселе ұғымына басқа мысал ретінде Л.М.Фридманның травтовкасы табылады, ол оны проблемалық жағдайды көшіріп алумен байланыстырады. Оның пікірі бойынша белгілі жағдайда белгілік модельдері құру үдерісінде ондағы ерекшеліктер нақтыланады жағдай мен бөгет мінездемелері арасындағы арақатынаспен байланыстарды орнату деп көрсетеді. [14] Осы ойларға сәйкес Л.И.Фридман келесі анықтаманы береді: Проблемалық жағдайдың қандай да белгілік моделін біз мәселе деп айтамыз. Бұл анықтамада кез келген мәселе белгілік моделді білдіретіндігі және оны басқа адамдарға беруге болатындығы көрінеді. Сондықтан да мәселені ойлап табуға, өзгертуге, қайта жасауға болады.
И.Я.Лернер мәліметтер мен ізделетін мәселе қарама-қайшылығында мынадай анықтама береді: Оқудағы танымдық мәселе-бұл өзіндік шешуде жаңа білімдер құруды белгілі шешу тәсілдері жаңа шешу тәсілдерін тудыруды болжамдайды. Бұндай анықтама мәдениет элементтері яғни білім берудің мағынасымен байланысты. Лернердің айтуынша кез келген танылатын есептің мағынасы болып проблема табылады, алайда, бұл анықтамаа бір типті мәселелерге қатысты, нақтылай түссек-танылатын дейді. Мәселе ұғымын талдауда авторлар оқу міндетінің түрлі аспектілерін алға тартады:
а) мәселе С.Л.Рубинштейн мен оның ізбасарлары трактовкаларында- бұл жағдайды тілдік қалыптастыру;
б) мәселе Я.Н.Леонтьев түсінігінде-белгілі жағдайларда берілген мақсат;
в) мәселе Я.А.Понаморев бойынша-бұл субъект әрекет жасауға тиісті жағдай;
г) мәселе Л.И.Фридман бағалауында-бұл шешу үшін беруге, елестеуге болатын жағдайды сипаттау;
д) мәселе И.Я.Лернер талқылауында--бұл білім беру мағынасы түзеу құралы.
К.В.Бардинаның монографиялық зерттеуінде оқу мәселесі оқу іс -әрекетінің құрамды бөлігі болып қарастырылады. Оның жазуы бойынша оқу мәселесінің болуы және оны үнемі басшылыққа алу-бұл оқушының оқу үшін ең бірінші меңгеруге тиісті болып табылады. Бұндай талқылаудағы оқу мәселесі ұғымы оқу мақсаты түсінігіне сәйкес келеді.
Е.И.Машбиц айтуынша: Оқу мәселесі үш түрлі есептер категорияларын белгілеу үшін қолданылады;ілімдер есебі, оқу және дидактикалық есептер мәселесі, ілімдер мақсатына жету үшін оқушыларымен талап етілген есептер.
Оқу мәселесі дегенде біз шындық құбылыстар немесе олардың мінездемелері туралы білімдер іздеу немесе қандайда іздеудегі практикалық нәтижені алудың талабын түсінеміз. Кейбір авторлар, оқу мәселесінің сипаттамасы оқу материалының мағынасымен байланысты-дейді (Чавдаров С.В).
Олардың түрлері есте сақтаумен, ойлаумен және оқушылар шығармасымен байланысты.(Загвязинский В.И.);оқу мәселесі-оқу үдерісінің негізгі тізбегі болып келеді, олар оқушыларды еске түсіру құралы ғана емес, өзіндік танымдық ойлау құралы болып көрінеді. Зерттеулерде қандай да ойлау іс-әрекеті белгілі бір теориялық немесе практикалық мәселені шешу деп көрсетіледі, мәселелер арқылы тәрбие беру, білім беру және дамытушы оқу мақсаттарын жүзеге асыру, сонымен нақты оқу үдерісіндегі мәселе оқу үдерісінің фокусы, тораптық сәті болып алға шығады. (Загвязинский В.И.); оқу мәселесі оқушылар іс-әрекетін білім алуға және олардың меңгерілу мақсатында, қабілеттерді қалыптастыру танымдық іс-әрекет тәжірибелерін қайта жасауға бағыттайды (Цетлин В.С).
Мәселенің бірінші құрамдас бөлігі болып белгілі мен белгісіз арасындағы қатынас табылады, олардың үш негізгі қасиеттері бар:
oo белгісіздік ізденісі басталатын, бастапқы;
oo белгісіздің іздеу үдерісі жүретін, ортаңғы;
oo белгілі бір нәтижемен аяқтайтын, соңғы.
Екінші құрамдас бөлігі болып мәселенің алданған әрекеті табылады. Іс әрекет көзқарасына мәселені шешу болашақ әрекет, қатынасын қанағаттандыру үшіін өткен мен бүгінгі тәжірибені біріктіруін айтамыз.
Мәселенің келесі құрамдас бөлігі болып оның талабы яғни белгілі мен белгісіз арасында байланысты табу үшін іс-әрекетті жүзеге асыру. Талап қалыптастыру кезінде қолданылатын сөздер:неге, ұқсастық неде, түсіндіріңізші, дәлелдеңіз. Шарттың өзі белгісіз бен белгілі арасындағы қатынасты байланыстыру тәсілі болып табылады.
Сөйтіп, кез келген мәселе келесі бөліктерді шарттар,әрекеттер, қатынастар, талаптарды қамтиды.
Дидактикалық әдебиеттерде есеп білім беру мақсаттарына жетуге бағытталған оқу әдісі болып табалады. Мысалы, И.Я.Лернер "педагогтар құрған танымдық есептер түріндегі педагогикалық конструкцияларды" ерекше бөліп көрсетеді. [4]
Есептің анықтамасына қатысты психологиялық көзқарасты негіз ете отырып, ол есепті түсінуді оның мазмұны мен құрылымы арқылы ашуға тырысады. Ол "танымдық есептер" ұғымын енгізген, оның өзі үш типке бөлінеді: оқу-танымдық, жаттығу және іздену-танымдық есептер. Барлық есептердің ортақ мазмұны "аралық мүше (аралық амалдар) арқылы шешімі табылатын, негізінде белгілі мен белгісіз араларындағы қарама-қайшылықтар жататын проблема" болып табылады [4].
Есептерді осылайша бөліктерге бөлу ісі И.Я.Лернердің "танымдық есептерді" танымдық қызметке оқытудың негізғі әдістерінің біріне жатқызуына негіз бола алады.
Дидактикалық түсінік бойынша оқыту әдістері оқыту үрдістері кезінде әдістер, тәсілдер және құралдар ретінде жүзеге асырылады. Әдістемелік әдебиеттерде есептер оқытудың құралы, оқыту әдістерін жүзеге асыруға арналған тәсілдер ретінде қарастырылады, осы жағдайларда есептердің функциялары айқындалады, олардың классификациясы беріледі, есептерді шығарудың тиімді әдістері талқыланады.
М Фридман есептердің құрылымдық элементтерін ерекше көрсетеді. "Проблемалық ахуалдың қандай да болмасын таңбалық моделін біз есеп деп атай алатын боламыз",- деп атап көрсетеді М.Фридман. [14] танымдық ойлау проблемаларына арналған еңбектерде (Дж.Брунер, К.Дункер, Е.И.Ефимов, В.П.Зинченко, Н.Нильсон, А.Ньюэлл, Д.А.Поспелов) есептік және есепті шығару жүйелері ерекше айқындалған. Есептік жүйеге есептің нысаны, шарты және талабы (берілген және ізделініп отырған шамалар), ал шығару жүйесіне-есептерді шығаруға қажетті алгоритмдік және эвристикалық ұйғарымдар құрудың көзі болып есептелетін ғылыми әдістер және құралдар жататын болады. Төменде есеп және оны шығару жүйелерінің құрылымдық бірліктері берілген (1-сурет)

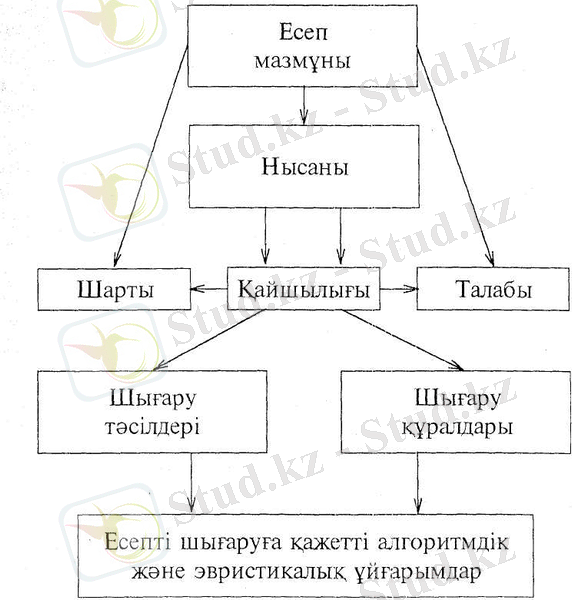
1-сурет
Есеп-күрделі диалектикалық жүйе, онда оның компоненттері (есептік және шығару жүйелері) өзара бірлікте, өзара байланысты, өзара тәуелді және әрекеттестік түрде келтірілген, сол компоненттердің әркайсысы өз кезегінде сол сияты динамикалық тәуелділікте болатын элементтерден: бір жағынан - есептің нысаны, шарты және талабынан, екінші жағынан оны шығару әдістерінен және құралдарынан тұрады.
Оқу үдерісінде қарапайым және күрделі есептерді, нақты тақырыптар мен тараулар бойынша есептерді, кешенді есептер мен пәнаралык мазмұндағы есептерді, түпкі нәтижені алу үшін алгоритмдік және эвристикалық ұйғарымдарды талап ететін есептерді пайдалану орын алды.
Есептің мәнін ұғыну оның құрылымын анықтау арқылы айқындалады. Кез келген есеп құрылымынан оның шартын (тұжырым) және талабын (сұрақ), немесе берілген шама және ізделіп отырған шаманы бөліп көрсетуге болады. Әдетте, есепте бір ғана шарт және талап болмай, бірнеше тәуелсіз тұжырымдар мен сұрақтар болуы жиі кездеседі. Мысал ретінде келесі алгебралық теңдеуді қарастырып, оның құрылымы мен мазмұнын талдайық.
Есеп. mt4-t3+m2t-m=0 теңдеуін шешіңдер.
Бұл есептің мазмұнында белгілі бір қатынаста болатын тұжырым мен сұрақ бар. Оны оқып, берілген шамалар мен ізделіп отырған шамаларды, яғни есептің шарты мен талабын бөліп көрсетеміз.
Бұл есептің берілуі бір талаптан тұрады. Бірақ оны талдау, одан шарт пен шынайы талапты жіктеп алуға мүмкіндік береді. Шарт: теңдеу, ал талап: осы теңдеуді шешу.
Әрине, мұнымен тоқтап қалуға болмайды, талдауды жалғастыру керек. Теңдеудің жазылуында екі әріп: m және t; әрпі бар. m әрпі -параметрді, яғни берілген есептің аумағында тұрақты ретінде қарастырылатын шаманы, t - өзгеру облысы сандар (мысалы, нақты сандар) жиыны (әдетте бұл жайт есепте калайда анықталады) болатын айнымалы шаманы белгілейді. Бұнымен бірге теңдеудің нені білдеретінін еске түсірген пайдалы. Сонда бұл есептің шарттары мьінадай:
1) m - параметр;
2) t - өзгеру облысы нақты сандар жиыны болатын айнымалы;
3) mt[4]-t[3]+m2 t-m=0 тендеуі t айнымалысы бар пікір.
Бұл есептің талабын былай тұжырымдауға болады: аталған пікір ақиқат болатындай t айнымалысының өзгеру облысындағы барлық мәндерін табу керек.
Есепті талдауды одан әрі жалғастыруға болады. "Берілген шарттар бойынша t айнымалысының мәндерін табу деген не?" деп сұрауға болады. Осы сұраққа жауап тауып, сонымен бірге есептің талабын да анықтаймыз. Ол мына түрге келеді: берілген айнымалысы бар пікірде t-ның орнына қойғанда m параметрінің барлық мүмкін мәндерінде оны ақиқат пікірге айналдыратындай m-нен тәуелді t [t(m)] -өрнектерін табу керек.
Көріп отырғандай, есепті талдау арқылы оның шарттары мен талаптарын жіктеп алуды әр түрлі деңгейде жүргізуге болады.
Есептің талдауын жүргізе отырып, есептің берілуінен оның шарттарын жіктеп, біз әр уакытта бұл талдауды есептің талабымен сәйкестендіріп, талапқа әрдайым көңіл аударып отыруымыз қажет. Басқаша айтқанда, есептің талдауы әрқашан есептің талаптарына бағытталған.
Есептердің дидактикалық жүйесін құру "классификация" ұғымын нактылап алуды қажет етеді. "Классификация (латынша classis - разряд, класс және fасіо -жасаймын, жіктеймін)-объектілердің ортақ белгілері мен олардың арасындағы заңды байланыстар негізінде құрылған, объектінің әр алуандығынан хабардар болуды және олар жайындағы білімнің қайнар көзі болып табылатын қандай да бір білім саласындағы матасқан ұғымдардың (объектілер мен құбылыстар тобының) жүйесі". Бұл жүйедегі ұғым, объект, құбылыстардың саны ұдайы өсіп, сапалық өзгешеліктері артып отыратындығына қарамастан, ішкі байланыстарының молая түсетін жиынтығы, аталмыш жүйені оның жұмыс істеу аясында мейлінше жинақы етіп, топтастырғыш және ақпараттық тұрғыдан мейлінше жетілдіре түседі.
Е.С.Валович, Е.В.Володарский, К.В.Даутова, Н.Ф.Искандеров, Е.И.Малолеткова, Х.Я.Марголин, Ф.И.Плешкан, Н.Н.Түлкібаева, А.В.Усова, Л.М.Фридман, т.б. зерттеулерін түбірлей талдау, жаратылыстану-математикалық циклдағы пәндердің оқу есептерін классификациялауға негіз береді. Оқу есептерін түрлі негіздерге сүйене отырып, жіктеуге болады Мақсаттың қойылымына орай есептерді аудиторияда және үйде шығарылатын, жаттығу, танымдық, өзіндік, танымдық және зерттеушілік есептер деп бөлуге болады.
Талаптың қойылымына орай есептерді ізделіндіні табуға, құрастыруға, дәлелдеуге арналған есептер деп жіктеген жөн.
Дәрежесі және күрделілік деңгейіне орай карапайым және күрделі деп бөлуге болады. Шығару әдістеріне қарай-алгоритмдік, эвристикалық есептер деп бөлуге болады.
Шығару тәсіліне қарай есептерді сандық есептер, графиктік және эксперименттік есептер, сурет-есептер деп айқындап қарастырған орынды.
Ұғымды қалыптастырудағы әдісі мен рөліне байланысты есептерді ұғым белгілерін нақтылауға, ұғым көлемі мен мазмұнын нақтылауға, ұғымды дифференциалдауға (бөлшектей қарастыруға), берілген ұғымның басқа ұғымдар мен байланысын анықтауға немесе нақтылауға арналған деп айыруға болады.
Жіктелуге ұсынылатын есеп түрлері құрылымы, құрамы, оқу үрдісінде атқаратын қызметі тұрғысынан біркелкі емес. Олардың өзі күрделілік дәрежесі әртүрлі құралған құрылым ретінде көрінетінін атап көрсету қажет. Мысалы, өндірістік-техникалық мазмұндағы есептер техникалық және политехникалық ұғымдарды қалыптастырудағы рөліне, өндірістің тиімділігінің экономикалық және экологиялық көрсеткіштеріне, техникалық ойлауды қалыптастыру мен дамытудағы рөліне т.с.с. қарай жіктелуі мүмкін. Графикалык есептерді жіктеу кезінде тәуелділіктің графигін салуға, графикалық интерпретацияларға, ізделіп отырған шаманы табуға, үрдісті талдауға, берілген график бойынша құбылыстарды, шаманың тәуелділігінің түрін және оның аналитикалық жазылуын анықтауға арналған есептерді айқындап көрсеткен орынды [16].
Егер оқу есептерін жіктеу мәселесі методологиялық, дидактикалық және әдістемелік деңгейлерде орындалған болса, онда ол ғылым дамуының қазіргі кезеңіне сәйкес шешілді деп санауға болады.
Оқу есептерін әдетте, шартты түрде стандарт және стандарт емес есептер деп ажырату орын алған. Енді осыған тоқталайық.
Есептерді оқушылардың ойлау қызметінің объектісі ретінде қарастырып, есеп элементтерінің арасындағы байланыстардың ерекшеліктеріне қарай А.Я.Цукарь оларды үш топқа бөледі:
1. Алгоритмдік.
2. Жартылай эвристикалық.
3. Эвристикалық.
Ол тікелей анықтама, ереже, формула, дәлелденген теоремалар жәрдемімен шығарылатын есептерді алгоритмдік топқа; шарттары сәл өзгертілген, оқушылар шығару жолын оңай табатын есептерді жартылай эвристикалық топқа; ал шарты мен талабының элементтерінің арасында (жасырын) байланыстар бар, шығару әдісі қосымша мәліметтерді, ойлауды қажет ететін есептерді эвристикалық топқа жатқызады.
Дидактикада оқушылардың таным қызметінің үш деңгейі бөліп көрсетіледі:
Бірінші деңгей - репродуктивті (төмен). Оқушылар есепті мүғалімнің басқаруымен ғана шығара алады.
Екінші деңгей - ішінара іздену (орта). Оқушылар есепті таныс жағдайлар үшін ғана шығара алады.
Үшінші деңгей - танымдық - зерттеушілік (жоғары). Оқушылар есепті жаңа таныс емес жағдайларда шығара алады.
Осы деңгейлерге және жоғарыдағы есептерді топтарға бөліп көрсетуге талдау жасау, таным қызметінің репродуктивті деңгейняе алгоритмдік есептер сәйкес келеді, ішінара-іздену деңгейіне жартылай эвристикалық есептер, ал шығармашылык-зерттеушілік деңгейге эвристикалық есептер (адекватты) пара-пар деген қорытынды жасауға мүмкіндік береді. Бірақ таным қызметі деңгейлері арасында да, сондай-ақ оларға (адекватты) пара-пар есептер топтарының арасында да дәл айқындалған шекара жоқ екендігін есте ұстаған жөн.
Заман талабы ғылым мен техниканың даму деңгейі әрбір адамға сапалы және терең білімнің, іскерліктің болуын қамтиды. Жастардың белсенді танымдық пен жұмыс істеуін және кеңінен ойлауға қабілетті болуын талап етеді. Сондықтан да мектептегі оқу процесінің негізгі мақсаты-арнайы педагогикалық әдістермен мақсатты және жүйелі түрде оқушылардың интелектін, танымдық ойлауын дамыту ғылыми көзқарасы мен белсенділігін қалыптастыру, әр адамның бойындағы туғанда пайда болған интуициясын әрі қарай дамытуға ықпал ету, оқушының табиғи қасиеттерін математикалық білім деңгейін тереңдету үшін оқытуды жоспарлы түрде ұйымдастыру, өз бетінше білім алу дағдыларының дамуына негізін салу болып табылады. танымдық -негізгі білім болғандықтан, оқушының білім деңгейіне сүйене отырып, олармен дайындық жұмыстарын жоспарлы түрде ұйымдастыру қажет. Білімге деген ынтасын, қызығушылығын, тұрақтылығын қалыптастыру жолдарын әр түрлі тапсырмаларды орындату арқылы бақылап отыру керек.
1 Оқушылардың өз бетінше ойлау білу есеп шығару мен оның сан қилы жолын іздестіру, олардың танымдық қабілетінің дамуының бір әдісі. Оқушының өз бетінше жұмыс істеуге үйрету пәнге қызығушылығын дамыту басты мақсат.
2 Оқушының математикадан білімін көтерудің ең басты шарты-оның пәнге қызығушылығын дамыту. Пәнге деген қызығушылығы болса ғана, бала оған көңіл қойып тыңдап, тереңдете оқып үйрене бастайды. Пәнге қызыққан оқушының білім сапасының жоғары болатыны белгілі. Мұғалім үнемі оқушының ойлау белсенділігін арттырып, білімге қызуғышылығын тудырғанда ған сабақ мақсатына жетеді.
3 Ал қызуғушылық туғызудың тәсілдері көп. Олар: сабақ барысында қолданылатын дидактикалық ойындар, математикалық сайыстар, эстафеталар, жарыстар, олимпиадалар, тіпті жақсы дайындықпен өткізген күнделікті сабақтар. Дұрыс ұйымдастырылған сабақ оқушының ой-өрісін кеңейтеді, өз деген сенімін күшейтеді.
Оқыту, тәрбие жұмыстары нәтижелі болу үшін мына мәселелерге көңіл бөліну тиіс:
1) жұмыс жоспарлы түрде, үздіксіз жүргізілуі тиіс;
2) жүргізілетін жұмыстарды еріктілік, саналық негізде ұйымдастырып, оқушының танымдық пен өз бетінше жұмыс істеуін қамтамасыз ету.
Көптеген математикалық ұғымдар ойлаудың дамуына белсенді әсер етеді. Мысалы, функциялық тәуелділік сияқты математикалық негізгі ұғымы қарастырылып отырған үдерістің сандық сапасын сипаттайды.
Математикалық құралдардың ең маңыздыларына жиындар теориясы, математикалық логикалық бастамасы, векторлар, жуықтап есептеу тәсілдері, координаттар әдісі, функцияны графиктік тәсілмен зерттеу, туынды, интеграл және т.б. жатады. Математикалық логика элементтері есептеуіш техникада, бағдарламалауда, электрондық техникада, математикалық статистикада, процестерді алгоритімдеуде және т.б. қолданылатынын айтуға да болады.
Математикада логикалық жағынан жүйелі, дәлелді, абстрактілі, ал оның тілі-анықтамалары, таңбасы, тұрақты тіркестері тұжырымды, жинақты.
Мұғалім танымның тек шама жағынан бейнеленген заңдылықтарын оқушыларға түсінікті тілмен, қарапайым мысалдар арқылы баяндауы қажет.
Математика мен оның әдістері өзімен сыбайлас ғылымдарды және басқа ғылымдарды да дамытуда маңызды рөл атқарады. Қазір математиканың қолданылмайтын жері кемде-кем деп айтуға болады. Бұрын математика ұғымдарының дерексіздігі мен жалпылығы, әмбебап қолданымдылығы мүмкіндік береді. Тек қатыстар мен математикалық символдарға тиісті жаңа мағына бере білу керек.
Мұғалім алгоритм, компьютер атауларын пайдалан отырып, оның тарихын әңгімелейді.
Барлық заманның ұлы математиктерінің бірі, алгебраның атасы, он цифрды таратушы шығыс энциклопедисі - Әл - Хорезми болып табылады.
Бабамыз Әл - Фараби, гректер Пифагор мен Евклидтен, үнді Ариабхатадан, өзбек Әл - Хорезмиден, араб Әл - Киндиден тәлім алған. Әл - Фараби мен Ариабхата табиғат құбылыстарын зерттеу құралы ретінде математиканы алған. Қозғалысты сипаттауға математиканы қолданған. Күн мен Айды есептеп, Жер шар пішіндес деп пікір айтқан.
Математикаға үйретудің бір мақсаты ғылымды үйрете отырып, соның негізінде ойлауды тәртіптеу. Нақтылы қажет нәрсеге оқушының ақыл - ой мүмкіндігін бағыттау. Онсыз ұмтылған мақсатқа жету қиын. Бұл жайында жазушы ғана емес, үлкен ұстаз Л.Н. Толстой былай дейді: Егер шәкірт мектепте жүргенде өз ақылымен ешнәрсе жасап үйренбесе, өмірде ол әрдайым еліктеуші, көргенін көшіруші ғана болып қала береді. Өйткені көшіріп үйренген адамдардың ішінде белгілі мағлұматтарды өз бетімен қолдана білетіндері аз.Яғни кімде-кім мұғалімнің үйреткенін меңгере отырып ойлап, өз бетінше де қорытынды жасап үйренсе, ол математиканы, есеп шығарудың әдістері мен жолдарын жақсы игеріп кете алады.[12]
Әркім өз мамандығына қарай, бір ғана нәрсені әр түрлі қабылдауы мүмкін. Мәселен, y=ax+b жазуы біреуге сызықты функцияны көрсетсе, екіншісіне түзуді көрсетеді. Ал үшінші біреуге мұны берілген телеграмма үшін төленетін ақшаның формуласы дейді. Мұнда: х-әрпі сөздің саны, құны, тиісті мекен жайға, иесіне жеткізу үшін төленетін ақы.
Математика сабағын жүргізгенде әр түрлі тәсілдерді тиімді пайдалана білу керек. Білім беруді ізгілендіру, оқыту әдістерін жетілдіруді, дамыта оқыту әдістері мен тәсілдерінің тиімді пайдалануын талап етеді.
Нақты ғылыми түсінік бойынша "есеп" ұғымы барлық ғылыми бағыттардың қажетті де ең маңызды элементі болып көрінеді, ал оны оқыту қызметі құрылымында қарастыру аталған ұғымды дидактикалық категорияға айналдырады.
Дидактикалық түсінік бойынша есеп бір мезгілде әрі таным объектісі, әрі оқушылардың танымдық қызметін басқару құралы болып табылады.
"Есеп" ұғымына мағына беру есепті шығаруға үйретудің теориялық негіздерін өндеу үшін жеткіліксіз болады. Амал тәсілін таңдау үрдісінен тұратын, "есепті шығару" ұғымын осы күнгі талаптар тұрғысынан түсінуді талдаудың да маңызы зор (Р.Бенерджи, Е.Н.Кабанова-Меллер, Д.Пойа, Ю.М.Колягин, А.А.Столяр, В.И.Крупич, Д.Толлингерова).
Оқыту теориясы мен есептерді шығаруды меңгеру практикасы арасында, есепті шығаруға үйрететін мұғалім қызметі мен есептерді шығаруды меңгеруге ұмтылған оқушылар біліктерінің арасында қарама-қайшылықтар бар, оны шешу шарттарының бірі оқушылардың "есепті шығару" ұғымын меңгерулері болып шығуы мүмкін.
Ғалым философтардың зерттеулерінде "шығару" және "есепті шығару" ұғымдарының бірнеше анықтамалары бар. Мысалы, С.Л.Рубинштейн кез келген ойлау актісін есеп шығаруға жатқызады, ал "оны шығару үрдісінде есептің объективті заттық мазмұнын жанамалайды және ойлау үрдісінде анықтайды" [10]. Ол әрі қарай былай деп жалғастырады: "Есепті шығару ой алдында тұрған қиындықтарды жеңу үшін қажетті, айтарлықтай жігерлі күш салуды үнемі талап етеді". Сонымен, психологияда есепті шығару есептің шарттары мен талаптары арасындағы қайшылықтарды шешуге бағытталған, кейбір жігерлі күш салу ретінде қарастырылады.
Есеп шығару теориясында "есепті шығару" түсінігі жөнінде екі көзкарас бар. Бірінші көзқарас бойынша әмбебап "есепті шешуге негізделеді және жетілдіріледі Екінші көзқарас бойынша есептердің жеке түрлері мен типтерін шығарудың әдістері мен тәсілдерін жетілдіруге жоғары баға беріледі.
Есепті шығаруды сипаттайтын құрылымдардың екі типі белгілі, олар: сыртқы және ішкі. Сыртқы құрылым есепті логикалық схемалар, алгоритмдік және эвристикалық ережелер арқылы сипаттайды, және сол аркылы есептік жүйені түрлендірудің тізбегін анықтайды. Ойлау операцияларын пайдалану ішкі құрылымды құруды қарастырады. Әртүрлі ғылымда (психологияда, жалпы және дербес дидактикаларда) есепті шығару үрдісінде осы құрылымдардың екеуін де қажетіне қарай пайдаланады. Есептерді шығару теориясында, өздерінің құрамдарына ойлау операциялары мен қатар логикалық операциялар да кіретін операциялық құрылымдарды құру орын алып отыр. Жалпы және дербес дидактикаларда есепті шығару үрдісін сипаттау үшін сырткы да, ішкі де құрылымдарды пайдаланады.
"Есепті шығару" ұғымын үрдіс және оның нәтижесі деп қарастыру керек. Үрдісті біз Н.И.Кондаковтың берген анықтамасы бойынша қарастырамыз. "Процесс (үдеріс) (латынша -processus - адым, өту, жылжу) - бірінің артынан бірі келетін даму моменттерінің үздіксіз, заңды және тізбектей жүзеге асырылатын ауысулары", мысалы, есепті шығару үдерісі, ойлау үдерісі. Осы түсінік бойынша шешу құрылымы, шешуді дайындаудан, оны қабылдаудан және жүзеге асырудан тұрады. Үдерісті жүзеге асыруға көмектесетін негізгі элементтер мыналар:
- амал тәсілдерінің бірін таңдап алу;
- амалды орындаудың мақсаттары мен құралдарының арасындағы өзара байланыстар мен өзара әрекеттестіктерді ұғыну;
- амалды модельдеу;
- амалдың салдарын бағалау;
- амалдың ұйғарылған нәтижесін талқылау;
- шешім кабылдау;
- шешімді жүзеге асыру;
- орындалатын амалды және сол амал арқылы алынған нәтижені талқылау.
Осыдан, есепті шығарудың білім алушының есепті қабылдап алғаннан бастап алынған нәтижені талқылағанға дейінгі қызметін қамтитындығы келіп шығады.
Есепті шығару есептің мазмұнында сипатталған объектіні түрлендіру үдерісі болып табылады.
Сонымен, есепті шығару дегеніміз объектіні түрлендіруге, есептің шарты мен талабы арасындағы қайшылықты шешуге бағытталған адамның ой қызметінің үдерісі болып табылады.
"Есепті шығару" ұғымы ойлау психологиясын да, оқыту психологиясын да өзінде біріктіреді. Есепті шығару үдерісінде адамның ойлау қызметінің негізгі заңдылықтары көрінеді, сонымен қатар, бір мезгілде білімді меңгеру және қолдану үдерісі жүріп жатады. Ойлау бұл жағдайда бірыңғай, сонымен қатар, әр түрлі операцияларда өтіп жататын, өзінің формасы бойынша әр алуан қызмет болып табылады. Олардың ең бастыларына анализ (талдау) бен синтез (біріктіру) жатады. Анализ дегеніміз заттар мен құбылыстарды оларды құрайтын бөліктерге ойша жіктей отырып, сол бөліктердің елеулі белгілерін, қатынастарын және элеметтерін айқындап көрсету болып табылады. Синтез элементтер араларындағы елеулі байланыстар мен қатынастарды аша отырып, анализ арқылы жіктелгендерді бүтін етіп қайта қалпына келтіруге мүмкіндік жасайды. Белгілі бір амалдарды орындағанда ойлау операцияларының бірінің екіншісіне қарағанда біршама басым келетіндігі туралы ғана айтуға болады, өйткені оларды шектеп тастау мүлде мүмкін емес. Анализ бен синтез бірлікте, белгілі бір өзара байланыста өмір сүре отырып, есеп шығару үрдісінде біртұтас аналитикалық-синтетикалық қызмет атқарады.
Есепті шығару үдерісінде Л.С.Выготскийдің, П.Я.Гальпериннің, А.Н.Леонтьевтің, А.А.Смирновтың, Б.М.Тепловтың еңбектерінде негізделген сана мен қызметтің бірлігі принципі байқалады.
Есепті шығару үдерісінде оқушыларда қызметтің құрылымдық элементтерін қалыптастыру қажет. Осы проблеманы жетілдіру барысында А.Н.Леонтьев, П.Я.Гальперин, Н.Ф.Талызина сияқты психологтардың еңбектерінде сипатталған қызметтің жүйелік-құрылымдық талдауларына сүйену керек. Олардың түсініктері бойынша қызмет құрылымы, өзінің құрамына әрекеттер жиынтығын қамтиды, ал олар өз кезегінде белгілі бір операциялар жүйесінен құралады.П.Я.Гальперин әрбір әрекетте бағыттаушы, атқарушы және бақылаушы құрамдас бөліктерді айқындайды. [17]
Ал И.С.Якиманская атқарушылық және жоспарлаушылық әрекетерді негіздейді.
В.М.Глушков операциялар типін олардың функционалдық міндеттеріне қарай талдайды, бұл жағдайда, ол сонымен бірге шартпен танысуды, шешу жоспарын құруды, шешуді жүзеге асыруды, орындалған шешудің және алынған жауаптың дұрыстығын тексеруді ерекше атап көрсетеді .
Л.М.Фридман есепті шығару барысындағы қызметтің келесі компоненттерін атап көрсетеді, олар: шартты талдау, шешу жоспарын іздестіру, шешуді жүзеге асыру, алынған нәтижені талдау. Біз Л.М.Фридманның көзқарасына қолдау бере отырып, есепті шығару барысындағы төрт әрекетті ерекше бөліп көрсетеміз, олар: есеппен танысу, есепті шығарудың жоспарын қүру, шығаруды жүзеге асыру, алынған нәтижені талдау.
Есептің мазмұнында кейбір берілген және ізделінді шамалар (шарт пен талап) беріледі де, олардың қатынасы және кейініректе бұл қатынастардың шешілуі арқылы есеп шығарудағы ой үрдісі аяқталады. Есепті шығару барысында оның шарты мен талабы арасындағы қатынасты білдіретін синтетикалық акт бастапкы болып көрінеді. Ал анализ осы қатынастар шегінде синтез арқылы жасалады. Физиологиялық көзқарас тұрғысынан алатын болсақ, аталған үдерістің негізі, анықталған динамикалық стереотиптің уақытша шартты байланыстарының белгілі бір жүйесін қалыптастыру болып табылады.
Есептерді шығару біліктілігін қалыптастыру негізіне уақытша шартты байланыстардың орнықты жүйелері жатады .
О.К.Тихомиров әрекеттер мен операцияларды сыртқы (практикалық) және ішкі (ойлау) түрлерге бөледі [18]. Әрекеттер мен операциялар кез келген қызметтің, соның ішінде есептерді шығару қызметінің де құрамдас элементтері болып табылады. Сонымен, қызметтің құрамдық элементтері не ішкі, не сыртқы үрдістер формасына ие болуы мүмкін. Қызмет, әрекеттер және операциялар есептерді шығару барысында күрделі функционалдық құрылулар ретінде көрінеді, олардың әрқайсысы белгілі бір жүйе болып табылады.
Есептерді шығарудың психологиялық теориясына талдау жасай отырып, әр әрекеттің өзінен негізгі операцияларды бөліп көрсетуге болады, олар: бағдарлау, жоспарлау, атқару, бақылау.
Жоғарыда айтылған төртінші операцияны өзін-өзі бақылаумен толықтыруды ұсынамыз, ол есепті шығаруды оқытуға жеке тұлғалық-бағдарлаушылық көзқарасты қамтамасыз етеді.
Есепті шығару үрдісінде ақиқат шындықтың заттары арасындағы қатынастар өрнегінің таңбалы-символдық (жасанды) формалары пайдаланылады. Есепті шығару өзіне, бейнелік ойлау мен сөз-логикалық ойлаулардың бірлігінде көрінетін формальды және семантикалық компоненттерді қамтиды. Есепті шығару үрдісінің формальды компоненттері әріптік, цифрлық немесе графикалык символдарға, олардың функционалдық тәуелділіктерін есепке ала отырып, жасалатын операциялар жүйесінен тұрады.
Есепті шығарудың семантикалык компоненттері есептің және оны шығарудың мазмұндарын мейлінше толық ұғынуға мүмкіндік беретін, сөз немесе көрнекіліктерге сүйеніп жүзеге асырады.
Жаңа белгісіз есепті шығару барысында, алдын ала дайындалған ережелер мен ұйғарымдарды пайдалану мүмкін емес жағдайларда, адам күрделі шешім қабылдау проблемасына тап болады. Күрделі және өте сирек кездесетін шешімдерді қабылдау проблемалары адам қызметінің барлық салаларында көрінеді. "Шешім кабылдау деп-көптеген критерийлер бойынша бағалану арқылы сипатталатын, альтернативті варианттар ішінен, оның бірін адамның таңдап алуының бір еселі үрдісін түсінеді",-деп атап көрсетеді О.И.Ларичев .
Есеп шығару жекелеген бөліктер мен сәттерден тұратын күрделі құрылым болып табылады. Ғалым-психолог Н.А.Менчинская есеп шығарудың мынадай сәттерін ажыратады: [19]
1. Есепті қабылдау нақты сұрақты қабылдау.
2. Есеп шарты ізделіндінің қасиеттерін сипаттауы керек.
3. Күрделі есептерді шығарғанда оның шартында байқалатын қарама -
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.