Механикалық тербелістердің дифференциалдық теңдеулері және олардың шешу әдістері


МЕХАНИКАЛЫҚ ТЕРБЕЛІСТЕРДІҢ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРІ
Мазмұны
Кіріспе. . . . 3
І. Тұрақты коэффициентті екінші ретті сызықты дифференциалдық
теңдеулер . . . 4
1. Тұрақты коэффициентті екінші ретті біртекті сызықты дифференциалдық
еңдеулер . . . 4
2. Тұрақты коэффициентті екінші ретті біртекті емес сызықты
дифференциалдық теңдеулер . . . 10
ІІ Механикалық тербелістердің дифференциалдық теңдеулері . . . 17
1. Ерікті және ерікті емес тербелістердің дифференциалдық теңдеулері . . . 17
2. Ерікті тербелістің дифференциалдық теңдеуінің шешімін зерттеу . . . 20
3. Еріксіз тербелістердің дифференциалдық теңдеуінің шешімін зерттеу . . . 25
4. Жалпыланған координатадағы ерікті тербелістердің дифференциялдық
теңдеуі . . . 30
5. Қосымшалар және мысалдар . . . 33
ІІІ. Кіші параметр әдісінің қолданылуы . . . 35
1. Энергетикалық теңдік . . . 35
2. Кіші параметр әдісінің қолданылуы . . . 36
3. Ван-дер Поль әдісі . . . 41
4. Орталау әдісін Фатудың негіздемесі . . . 45
5. Орталау әдісін Фатудың негіздемесі . . . 52
Қорытынды. . . . 60
Әдебиеттер. . . . 61
Кіріспе
Өзектілігі. Тербелістердің дифференциалдық теңдеулерін құрудың өзі маңызды мәселе. Ал құрылған дифференциалдық теңдеулерін шешіп және оны талдау, яғни зерттеу екінші бір өзекті мәселе. Сонда шешімдер қандай жағдайда тербелісті береді және қандай жағдайда тербеліс болмайды. Мінеки, осыларды анықтау өте маңызды мәселе болып табылды.
Мақсаты. Бірінші мақсат механикалық тербелістерге сәйкес келетін дифференциалдық теңдеуді құру болса, екінші мақсат құрылған дифференциалдық теңдеулерді шешу және ол табылған шешімдерді зерттеу болып табылады.
Міндеті. Негізгі міндет құрылған дифференциалдық теңдеулерді шеше білу және ол шешілген шешімдері зерттей білу керек, яғни қандай жағдайда тербелістер бар болады, ал қандай жағдайда тербелістер жоқ болады.
Құрылымы. Бұл дипломдық жұмыс кіріспеден, бірінші, екінші, үшінші бөлімдерден және қортындыдан шығады. Соңында пайдаланған әдебиеттер тізімі келтірілген. Сонымен бірге әрбір бөлім бірнеше пунктерден құралған. Әр пунктінің соңында есептер шығарып көрсеткен. Сөйтіп, жұмыс осындай тәртіппен, яғни осындай ретпен баяндалған.
І. Тұрақты коэффициентті 2 - ретті сызықты дифференциалдық
теңдеулер.
1. Тұрақты коэффициентті 2 - ретті біртекті сызықты дифференциал-
дық теңдеулер.
Анықтама. Мына түрдегі теңдеу
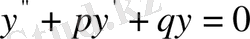 (1)
(1)
тұрақты коэффициентті 2 - ретті біртекті сызықты дифференциалдық теңдеу деп аталады, егер коэффициенттер p мен q нақты тұрақты сандар болса.
Бізге белгілі, бұл теңдеудің жалпы шешімін табу үшін оның сызықты тәуелсіз екі дербес шешімін табу жеткілікті.
- теңдеудің дербес шешімін мына түрде іздейміз:
, (2)
мұндағы
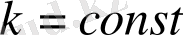 . Сонда
. Сонда
 .
.
Осыларды (1) теңдеуге апарып қойып, мынаған келеміз:
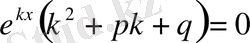 .
.
Бұл жерден
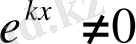 екендігін ескерсек, мынау шығады:
екендігін ескерсек, мынау шығады:
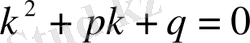 . (3)
. (3)
Сондықтан, егер
 саны (3) теңдеуді қанағаттандыратын болса, онда
саны (3) теңдеуді қанағаттандыратын болса, онда
 (1) теңдеудің шешімі болады. (3) теңдеу (1) теңдеуге сәйкес характеристикалық теңдеу деп аталады.
(1) теңдеудің шешімі болады. (3) теңдеу (1) теңдеуге сәйкес характеристикалық теңдеу деп аталады.
Характеристикалық теңдеу квадраттық теңдеу болып тұр. Сондықтан оның екі түбірі болады. Оларды
 және
және
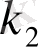 арқылы белгілейміз. Сонда олар:
арқылы белгілейміз. Сонда олар:
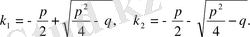
Бұл жерде мынадай жағдайлар болуы мүмкін:
І.
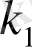 мен
мен
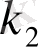 - нақты және әртүрлі
- нақты және әртүрлі
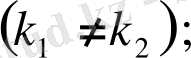
ІІ.
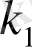 мен
мен
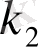 - комплекс сандар;
- комплекс сандар;
ІІІ.
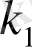 мен
мен
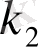 - тең нақты сандар
- тең нақты сандар
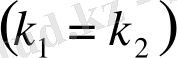 .
.
Әрбір жағдайды жеке - жеке қарастырамыз.
І. Характеристикалық теңдеудің түбірлері нақты және әр түрлі:
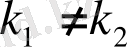 .
.
Бұл жағдайда дербес шешімдері мына функциялар болады:
 .
.
Бұл шешімдер сызықты тәуелсіз, себебі
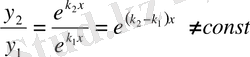 .
.
Сондықтан, жалпы шешім мына түрде болады:
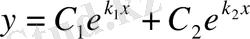 .
.
Мысал 1.
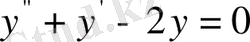 дифференциалдық теңдеуі берілген.
дифференциалдық теңдеуі берілген.
Шешу. Характеристикалық теңдеу мына түрде болады:
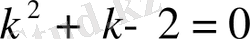 .
.
Характеристикалық теңдеудің түбірлерін табалық:
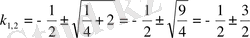 ;
;
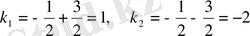 .
.
Бұл түбірлер нақты және әртүрлі. Сонда:
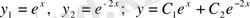 .
.
ІІ. Характеристикалық теңдеудің түбірлері комплекстік сандар.
Комплекстік түбірлер қос - қостан түйіндес болып келеді.
Оларды
 деп белгілейік, мұндағы
деп белгілейік, мұндағы
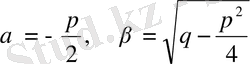 .
.
Дербес шешімдерді мына түрде жазуға болады:
 . (4)
. (4)
Бұл функциялар (1) дифференциалдық теңдеуді қанағаттандыратын нақты аргументті комплекстік функциялар.
Тұжырым. Егер қандай да бір нақты аргументті комплекстік функция
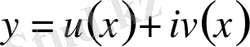 (5)
(5)
- теңдеуді қанағаттандырса, онда ол теңдеудіпен
функцияларының әр қайсысы да қанағаттандырады.
Шынында, (5) өрнекті (1) теңдеуге апарып қойып, мынаған келеміз:
 немесе
немесе
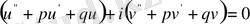 .
.
Бірақ, комплекстік функция тек сол кезде нольге тең болады, егер оның нақты бөлігі мен жорамал бөлігі нольге тең болса, яғни
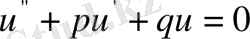 ,
,
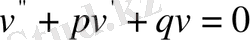 .
.
Бұдан көреміз,
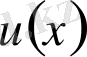 пен
пен
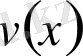 - тің әрқайсысы (1) теңдеудің шешімі болып табылатынын.
- тің әрқайсысы (1) теңдеудің шешімі болып табылатынын.
Комплекстік шешімдер (4) - ті нақты және жорамал бөліктердің қосын-дысы түрінде жазып аламыз:
 ,
,
 ,
,
яғни
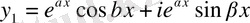 ,
,
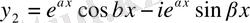 . (6)
. (6)
Жоғарыда дәлелденген тұжырым бойынша (1) теңдеудің дербес шешім-дері болып мына нақты функциялар табылады:
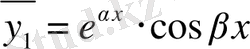 ,
,

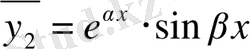 .
.

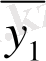 мен
мен
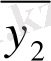 функциялары сызықты тәуелсіз, себебі
функциялары сызықты тәуелсіз, себебі
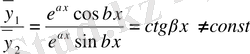 .
.
Сондықтан, характеристикалық теңдеудің түбірлері комплекстік сандар болып келгенде (1) теңдеудің жалпы шешімі мына түрде болады:
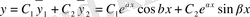
немесе
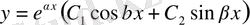 , (7)
, (7)
мұндағы
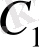 мен
мен
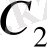 - кез келген тұрақтылар.
- кез келген тұрақтылар.
(7) шешімнің мынадай дербес жағдайының маңызы үлкен. Ол жағдай мынау: характеритикалық теңдеудің түбірлері таза жорамал болған жағдай.
Егер (1) теңдеуде
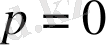 болса, онда осы дербес жағдай келіп шығады:
болса, онда осы дербес жағдай келіп шығады:
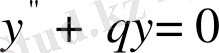 .
.
Бұл дифференциалдық теңдеудің характеристикалық теңдеуі мына түрде бо-лады:
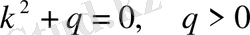 .
.
Бұл характеристикалық теңдеудің түбірлері:
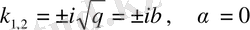 .
.
(7) шешім мына түрге келеді:
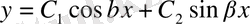 .
.
Мысал 2.
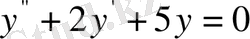 теңдеуі берілген. Жалпы шешімін және мына
теңдеуі берілген. Жалпы шешімін және мына
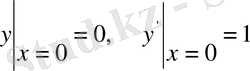 бастапқы шартты қанағаттандыратын дербес шешімін тап.
бастапқы шартты қанағаттандыратын дербес шешімін тап.
Шешу. 1) характеристикалық теңдеуін жазалық:
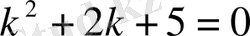 .
.
Түбірлерін табалық:
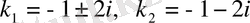 . Сондықтан, жалпы шешімі мынадай болады:
. Сондықтан, жалпы шешімі мынадай болады:
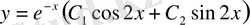 .
.
2) Енді дербес шешімін табамыз. Ол үшін бастапқы шартты пайда-ланамыз:
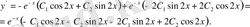
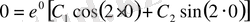 , бұдан
, бұдан
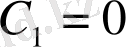 .
.
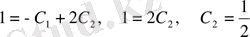 .
.
Сөйтіп, іздеп отырған дербес шешім мынау:
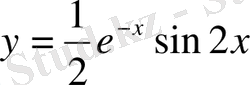 .
.
Мысал 3.
 теңдеуі берілген. Жалпы шешімін және мына
теңдеуі берілген. Жалпы шешімін және мына
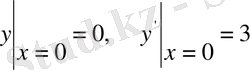 бастапқы шартты қанағаттандыратын дербес шешімін тап.
бастапқы шартты қанағаттандыратын дербес шешімін тап.
Шешу.
Характеристикалық теңдеуін жазалық:
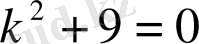 .
.
Түбірлерін табалық:
 .
.
Жалпы шешім мынадай болады:
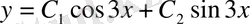 .
.
Енді дербес шешімін табалық:
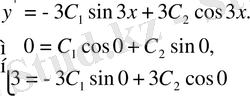
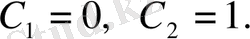
Сонда дербес шешім:
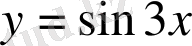 .
.
ІІІ. Характеристикалық теңдеудің түбірлері нақты және өзара тең, яғни
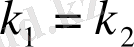 .
.
Алдыңғы талқылау негізінде бір дербес шешімі мынау
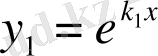 . Осы дер-бес шешіммен сызықтық тәуелсіз болатын екінші дербес шешімді табу керек. Екінші дербес шешім үшін
. Осы дер-бес шешіммен сызықтық тәуелсіз болатын екінші дербес шешімді табу керек. Екінші дербес шешім үшін
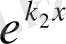 - ті алуға болмайды, себебі
- ті алуға болмайды, себебі
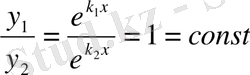 , яғни сызықтық тәуелді.
, яғни сызықтық тәуелді.
Екінші дербес шешімді мына түрде іздейміз:
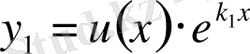 ,
,
мұндағы
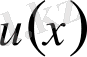 - белгісіз функция, табуды талап етеді.
- белгісіз функция, табуды талап етеді.
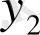 - ден екі рет туынды аламыз:
- ден екі рет туынды аламыз:
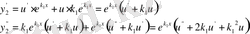
Осы
 - тің өрнектерін (1) теңдеуге апарып қойып, мынаған келеміз:
- тің өрнектерін (1) теңдеуге апарып қойып, мынаған келеміз:
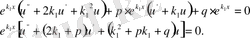
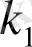 - харатеристикалық теңдеудің еселі түбірі болғандықтан
- харатеристикалық теңдеудің еселі түбірі болғандықтан
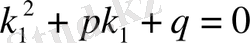 және
және
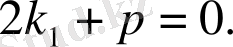
Осыларды ескерсек, жоғарыдағы тік жақшаның іші мына түрге келеді:
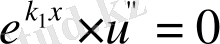 . Бұдан
. Бұдан
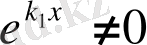 болғандықтан
болғандықтан
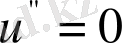 . Бұл теңдеуді интегралдасақ, мынаған келеміз:
. Бұл теңдеуді интегралдасақ, мынаған келеміз:
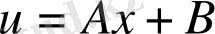 . Бізге
. Бізге
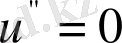 теңдеуінің кез келген дербес шешімі жеткілікті. Сондықтан,
теңдеуінің кез келген дербес шешімі жеткілікті. Сондықтан,
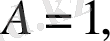
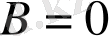 деп алсақ та болады. Олай болса,
деп алсақ та болады. Олай болса,
 болады да,
болады да,
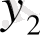 үшін мынаны аламыз:
үшін мынаны аламыз:
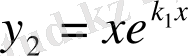 . Бұл
. Бұл
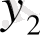 мен
мен
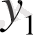 сызықтық тәуелсіз, себебі
сызықтық тәуелсіз, себебі
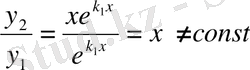 .
.
Олай болса бұл жағдайда жалпы шешім мына түрде болады:
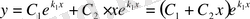 .
.
Мысал 4.
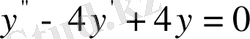 теңдеуі берілген.
теңдеуі берілген.
Шешу. Характеристикалық теңдеуін жазалық:
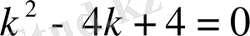 .
.
Оның түбірлерін табамыз:
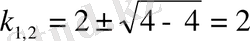 , яғни
, яғни
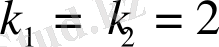 .
.
Жалпы шешімі
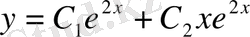 , яғни
, яғни
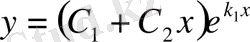 болады.
болады.
2. Тұрақты коэффициентті екінші ретті біртекті емес сызықты
дифференциалдық теңдеулер.
Анықтама. Айнымалы коэффициентті 2 - ретті біртекті емес сызықтық дифференциалдық теңдеу деп мына түрдегі
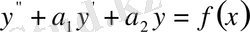 (1)
(1)
теңдеуді айтамыз, егер
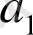 мен
мен
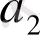 х - тің функциялары болса.
х - тің функциялары болса.
Бұл теңдеудің жалпы шешімінің құрылысы мына теоремамен анық-талады.
Теорема.
Біртекті емес сызықтық (1) теңдеудің жалпы шешімі екі түрлі шешімнің қосындысынан тұрады; бірі (1) теңдеуге сәйкес біртекті теңдеудің жалпы шешімі
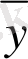 да, екншісі (1) - дің өзінің қандай да бір
да, екншісі (1) - дің өзінің қандай да бір
дербес шешімі
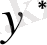 , яғни мына формуламен
, яғни мына формуламен
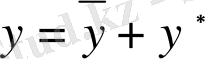
табылады.
Дәлелдеу. (1) - дің сәйкес біртекті теңдеуі:
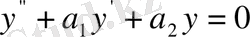 . (2)
. (2)
Бізге мына қосынды
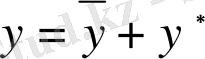 (3)
(3)
(1) - дің жалпы шешімі екендігін дәлелдеу керек.
Алдымен, (3) өрнек (1) - дің шешімі екендігін көрсетелік. Ол үшін
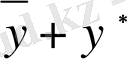 қосындысын (1) теңдеуге апарып қоямыз. Сонда мынаған келеміз:
қосындысын (1) теңдеуге апарып қоямыз. Сонда мынаған келеміз:
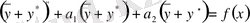
немесе
 . (4)
. (4)
 - (2) - нің шешімі болғандықтан (4) - тегі бірінші жақшаның іші нольге тең, ол
- (2) - нің шешімі болғандықтан (4) - тегі бірінші жақшаның іші нольге тең, ол
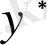 - (1) - дің шешімі болғандықтан екінші жақшаның іші
- (1) - дің шешімі болғандықтан екінші жақшаның іші
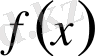 - ке тең. Сондықтан, (4) - тен мынау шығады:
- ке тең. Сондықтан, (4) - тен мынау шығады:
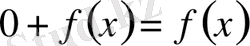 немесе
немесе
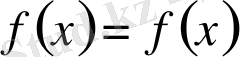 . Сөйтіп, теореманың бірінші бөлімі дәлелденді.
. Сөйтіп, теореманың бірінші бөлімі дәлелденді.
Енді (3) өрнек (1) теңдеудің жалпы шешімі екендігін дәлелдейміз, яғни (3) - тің құрамына кіретін кез келген тұрақтыларды сондай етіп таңдап алуға болады, сонда бұған сәйкес келетін шешім мына бастапқы шарттарды қанағаттандыратын болсын:
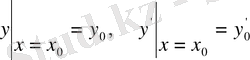 , (5)
, (5)
мұндағы
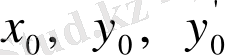 - кез келген берілген сандар.
- кез келген берілген сандар.
 - ті мына түрде
- ті мына түрде
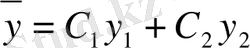 жазуға болатынын ескеріп, (3) - ті былай жазып алалық:
жазуға болатынын ескеріп, (3) - ті былай жазып алалық:
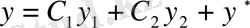 ,
,

(5) бастапқы шарттарға сәйкес
 - ті былай жазалық:
- ті былай жазалық:
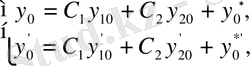
мұндағы
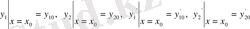 .
.
Бұл жүйеден
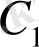 мен
мен
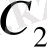 - ні табуға болады, өйткені оның анықтауышы нольден өзгеше (
- ні табуға болады, өйткені оның анықтауышы нольден өзгеше (
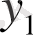 мен
мен
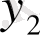 - сызықты тәуелсіз) . Сонымен бірге ол анықтауыш Вронский анықтауышы. Сондықтан, мына жүйе
- сызықты тәуелсіз) . Сонымен бірге ол анықтауыш Вронский анықтауышы. Сондықтан, мына жүйе
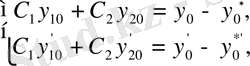 (6)
(6)
анық бір шешімге ие. Осы табылған
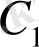 мен
мен
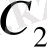 - ні (3) - тегі орындарына апа-рып қойсақ, онда шыққан дербес шешім берілген бастапқы шартты қанағат-тандырады. Сөйтіп, теорема толық дәлелденді.
- ні (3) - тегі орындарына апа-рып қойсақ, онда шыққан дербес шешім берілген бастапқы шартты қанағат-тандырады. Сөйтіп, теорема толық дәлелденді.
Сөйтіп, егер (2) біртекті теңдеудің жалпы шешімі белгілі болса, онда (1) теңдеуді интегралдаудағы негізгі мәселе (1) - дің қандай да бір дербес шешімін табудан тұрады екен.
Енді біртекті емес теңдеудің дербес шешімін табатын жалпы әдісті көрсетеміз. Бұл әдісті тұрақтыларды вариациялау әдісі деп атайды. Міне енді осы әдісті баяндауға кірісеміз.
Кез келген тұрақтыларды вариациялау әдісі.
(2) біртекті теңдеудің жалпы шешімін жазып аламыз:
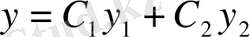 (7)
(7)
(1) біртекті емес теңдеудің дербес шешімін (7) түрінде іздейміз, бірақ ондағы
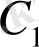 мен
мен
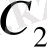 х - тің функциялары деп қарастырылады, яғни
х - тің функциялары деп қарастырылады, яғни
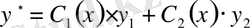

деп қарастырылады. Осы
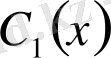 пен
пен
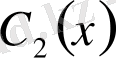 - ті тапсақ, онда
- ті тапсақ, онда
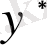 табылған болады.
табылған болады.
 тен х бойынша уынды аламыз:
тен х бойынша уынды аламыз:
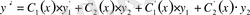 .
.
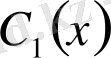 пен
пен
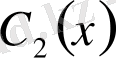 белгісіз функцияларын сондай етіп таңдап аламыз, сонда мына теңдік
белгісіз функцияларын сондай етіп таңдап аламыз, сонда мына теңдік
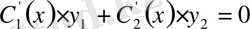 (8)
(8)
орындалатын болсын. Егер осы қосымша шартты ескерсек, онда
 мына түрге келеді:
мына түрге келеді:
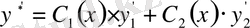 .
.
Енді осы
 - тен туынды алсақ, мынау шығады:
- тен туынды алсақ, мынау шығады:
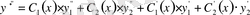 .
.
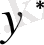 ,
,
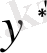 ,
,
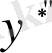 - тарды (1) - ге апарып қойып, мынаған келеміз
- тарды (1) - ге апарып қойып, мынаған келеміз
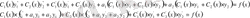
Алдыңғы екі жақшаның ішіндегі өрнектер нольге тең, себебі
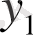 мен
мен
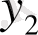 - біртекті теңдеудің шешімдері. Сондықтан, соңғы теңдік мына түрге келеді:
- біртекті теңдеудің шешімдері. Сондықтан, соңғы теңдік мына түрге келеді:
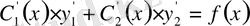 . (9)
. (9)
Сөйтіп,
 функциясы біректі емес теңдеу (1) - дің шешімі болады тек сонда ғана, егер
функциясы біректі емес теңдеу (1) - дің шешімі болады тек сонда ғана, егер
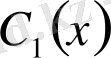 пен
пен
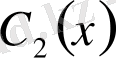 функциялары мына
функциялары мына
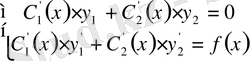
жүйенің шешімі болса. Бұл жүйенің анықтауышы Вронский анықтауышы және ол нольден өзгеше, себебі
 мен
мен
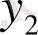 (2) теңдеудің сызықтық тәуелсіз дербес шешімдері. Сондықтан, ол жүйе
(2) теңдеудің сызықтық тәуелсіз дербес шешімдері. Сондықтан, ол жүйе
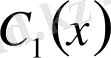 пен
пен
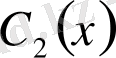 бір мәнді табылады, яғни:
бір мәнді табылады, яғни:
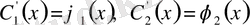 .
.
Бұларды интегралдап, мынаған келеміз:
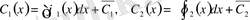 ,
,
мұндағы
 пен
пен
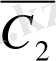 - кез келген тұрақтылар.
- кез келген тұрақтылар.
 =
=
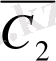 =0 десек те болады. Сонда
=0 десек те болады. Сонда
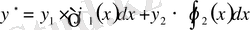 .
.
Мысал.
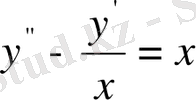 теңдеудің жалпы шешімін тап.
теңдеудің жалпы шешімін тап.
Шешу.
Алдымен мына біртекті теңдеудің жалпы шешімін табамыз.
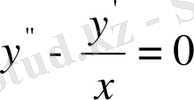 . Бұны
. Бұны
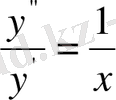 деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
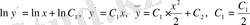 , яғни
, яғни
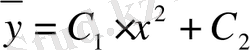 .
.
Бұл соңғы өрнек біртекті теңдеудің жалпы шешімі. Енді
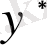 - ны іздейміз. Ал
- ны іздейміз. Ал
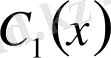 пен
пен
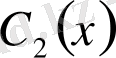 - ті мына жүйеден табамыз:
- ті мына жүйеден табамыз:
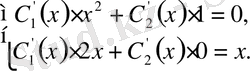
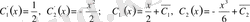 .
.
Егер бұл жерде
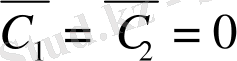 десек, онда
десек, онда
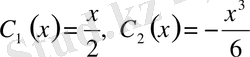 болады.
болады.
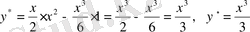 .
.
Енді тұрақты коэффициентті екінші ретті біртекті емес сызықтық диф-ференциалдық теңдеулерді қарастырамыз.
Анықтама. Тұрақты коэффициентті екінші ретті біртекті емес сызықтық
дифференциалдық теңдеу деп мына түрдегі
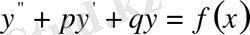 (1)
(1)
теңдеуді айтады, егер коэффициенттер
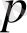 мен
мен
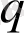 нақты сандар болса.
нақты сандар болса.
Мұның алдында біртекті емес теңдеудің дербес шешімін табатын жалпы әдіс көрсетіледі. Тұрақты коэффициентті біртекті емес теңдеулердің дербес шешімін табу кейбір дербес жағдайларда оңай жолмен шешіледі, яғни интегралдау амалын қолданбастан. Қазір (1) теңдеу үшін сондай жағдайлардың түрлерін қарастырамыз.
І. Айталық,
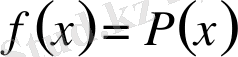 (2)
(2)
болсын, мұндағы
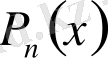 -
-
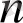 дәрежелі көпмүшелік, яғни
дәрежелі көпмүшелік, яғни
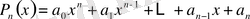 .
.
А) егер ноль саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
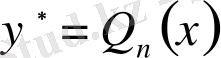 ,
,
яғни
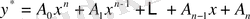 (3)
(3)
мұндағы
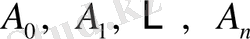 - уақытша белгісіз коэффициенттер.
- уақытша белгісіз коэффициенттер.
Б) егер ноль саны характеристикалық теңдеудің түбірі болма, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
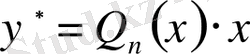 .
.
ІІ. Айталық,
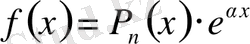 (4)
(4)
болсын, мұндағы
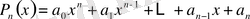 .
.
А) егер
 саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
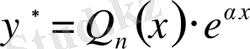 , (5)
, (5)
мұндағы
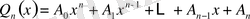 .
.
Б) егер
 саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
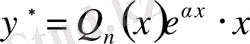 . (6)
. (6)
ІІІ. Айталық,
 болсын.
болсын.
А) егер
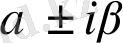 характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
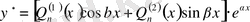
Б) егер
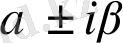 характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
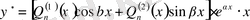 .
.
ІV. Айталық,
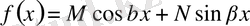 болсын, мұндағы
болсын, мұндағы
 мен
мен
 - тұрақтылар.
- тұрақтылар.
А) егер
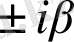 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
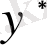 - ны мына түрде іздейміз:
- ны мына түрде іздейміз:
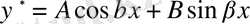 , мұндағы А мен В - белгісіз коэффици-енттер.
, мұндағы А мен В - белгісіз коэффици-енттер.
Б) егер
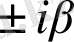 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
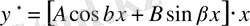 деп іздейміз.
деп іздейміз.
Мысал 1.
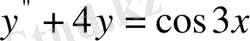 теңдеуін шеш.
теңдеуін шеш.
Шешу.
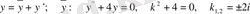 .
.
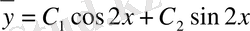 .
.
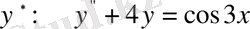
теңдеуінің кез келген бір дербес шешімі.
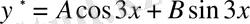 деп іздейміз.
деп іздейміз.
 .
.
Осыларды берілген теңдеуге апарып қоямыз. Сонда
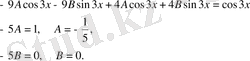
Бұдан
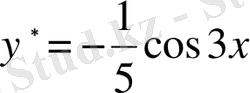 .
.
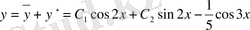 .
.
Мысал 2.
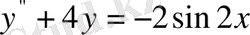 теңдеуін шеш.
теңдеуін шеш.
Шешу.
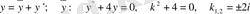 .
.
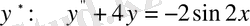
теңдеуінің кез келген бір дербес шешімі.
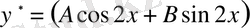 деп іздейміз.
деп іздейміз.
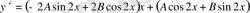

Осыларды берілген теңдеуге апарып қоямыз. Сонда

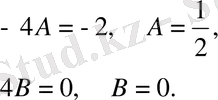
Бұдан
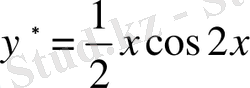 .
.
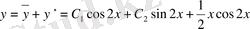 .
.
Мысал.
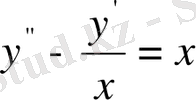 теңдеудің жалпы шешімін тап.
теңдеудің жалпы шешімін тап.
Шешу.
Алдымен мына біртекті теңдеудің жалпы шешімін табамыз.
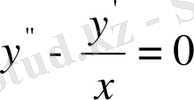 . Бұны
. Бұны
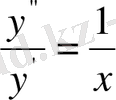 деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
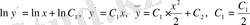 , яғни
, яғни
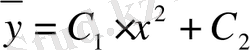 .
.
Бұл соңғы өрнек біртекті теңдеудің жалпы шешімі. Енді
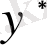 - ны іздейміз. Ал
- ны іздейміз. Ал
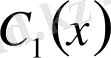 пен
пен
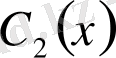 - ті мына жүйеден табамыз:
- ті мына жүйеден табамыз:
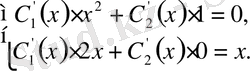
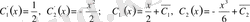 .
.
Егер бұл жерде
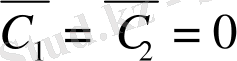 десек, онда
десек, онда
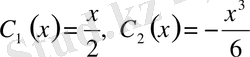 болады.
болады.
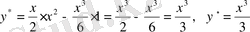 .
.
Енді тұрақты коэффициентті екінші ретті біртекті емес сызықтық диф-ференциалдық теңдеулерді қарастырамыз.
Анықтама. Тұрақты коэффициентті екінші ретті біртекті емес сызықтық
дифференциалдық теңдеу деп мына түрдегі
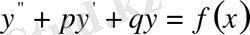 (1)
(1)
теңдеуді айтады, егер коэффициенттер
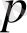 мен
мен
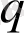 нақты сандар болса.
нақты сандар болса.
Мұның алдында біртекті емес теңдеудің дербес шешімін табатын жалпы әдіс көрсетіледі. Тұрақты коэффициентті біртекті емес теңдеулердің дербес шешімін табу кейбір дербес жағдайларда оңай жолмен шешіледі, яғни интегралдау амалын қолданбастан. Қазір (1) теңдеу үшін сондай жағдайлардың түрлерін қарастырамыз.
І. Айталық,
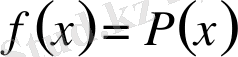 (2)
(2)
болсын, мұндағы
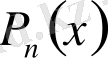 -
-
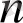 дәрежелі көпмүшелік, яғни
дәрежелі көпмүшелік, яғни
 .
.
А) егер ноль саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
 ,
,
яғни
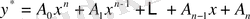 (3)
(3)
мұндағы
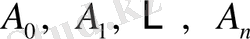 - уақытша белгісіз коэффициенттер.
- уақытша белгісіз коэффициенттер.
Б) егер ноль саны характеристикалық теңдеудің түбірі болма, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
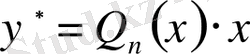 .
.
ІІ. Айталық,
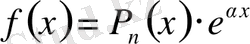 (4)
(4)
болсын, мұндағы
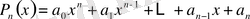 .
.
А) егер
 саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
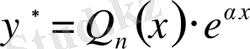 , (5)
, (5)
мұндағы
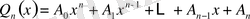 .
.
Б) егер
 саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
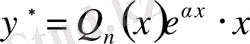 . (6)
. (6)
ІІІ. Айталық,
 болсын.
болсын.
А) егер
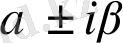 характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
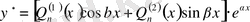
Б) егер
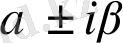 характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
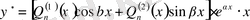 .
.
ІV. Айталық,
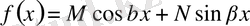 болсын, мұндағы
болсын, мұндағы
 мен
мен
 - тұрақтылар.
- тұрақтылар.
А) егер
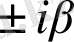 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
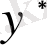 - ны мына түрде іздейміз:
- ны мына түрде іздейміз:
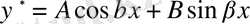 , мұндағы А мен В - белгісіз коэффици-енттер.
, мұндағы А мен В - белгісіз коэффици-енттер.
Б) егер
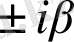 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
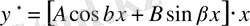 деп іздейміз.
деп іздейміз.
Мысал 1.
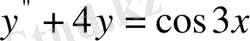 теңдеуін шеш.
теңдеуін шеш.
Шешу.
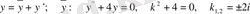 .
.
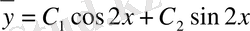 .
.
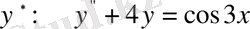
теңдеуінің кез келген бір дербес шешімі.
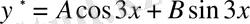 деп іздейміз.
деп іздейміз.
 .
.
Осыларды берілген теңдеуге апарып қоямыз. Сонда
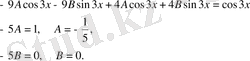
Бұдан
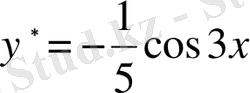 .
.
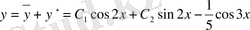 .
.
Мысал 2.
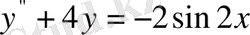 теңдеуін шеш.
теңдеуін шеш.
Шешу.
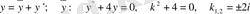 .
.
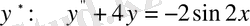
теңдеуінің кез келген бір дербес шешімі.
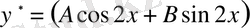 деп іздейміз.
деп іздейміз.
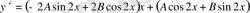

Осыларды берілген теңдеуге апарып қоямыз. Сонда

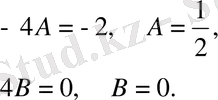
Бұдан
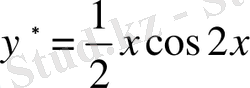 .
.
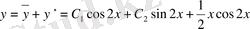 .
.
Мысал.
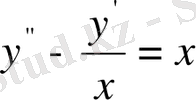 теңдеудің жалпы шешімін тап.
теңдеудің жалпы шешімін тап.
Шешу.
Алдымен мына біртекті теңдеудің жалпы шешімін табамыз.
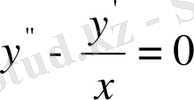 . Бұны
. Бұны
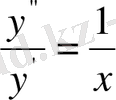 деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
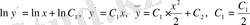 , яғни
, яғни
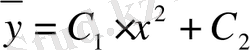 .
.
Бұл соңғы өрнек біртекті теңдеудің жалпы шешімі. Енді
 - ны іздейміз. Ал
- ны іздейміз. Ал
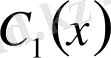 пен
пен
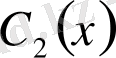 - ті мына жүйеден табамыз:
- ті мына жүйеден табамыз:
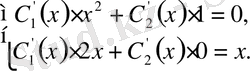
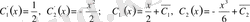 .
.
Егер бұл жерде
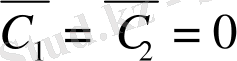 десек, онда
десек, онда
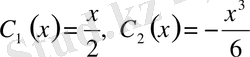 болады.
болады.
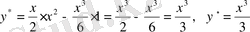 .
.
Енді тұрақты коэффициентті екінші ретті біртекті емес сызықтық диф-ференциалдық теңдеулерді қарастырамыз.
Анықтама. Тұрақты коэффициентті екінші ретті біртекті емес сызықтық
дифференциалдық теңдеу деп мына түрдегі
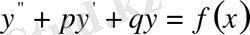 (1)
(1)
теңдеуді айтады, егер коэффициенттер
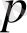 мен
мен
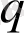 нақты сандар болса.
нақты сандар болса.
Мұның алдында біртекті емес теңдеудің дербес шешімін табатын жалпы әдіс көрсетіледі. Тұрақты коэффициентті біртекті емес теңдеулердің дербес шешімін табу кейбір дербес жағдайларда оңай жолмен шешіледі, яғни интегралдау амалын қолданбастан. Қазір (1) теңдеу үшін сондай жағдайлардың түрлерін қарастырамыз.
І. Айталық,
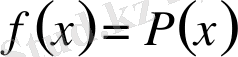 (2)
(2)
болсын, мұндағы
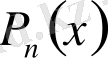 -
-
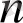 дәрежелі көпмүшелік, яғни
дәрежелі көпмүшелік, яғни
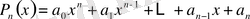 .
.
А) егер ноль саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
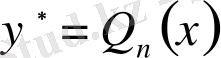 ,
,
яғни
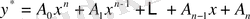 (3)
(3)
мұндағы
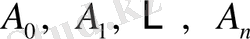 - уақытша белгісіз коэффициенттер.
- уақытша белгісіз коэффициенттер.
Б) егер ноль саны характеристикалық теңдеудің түбірі болма, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
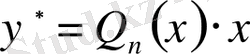 .
.
ІІ. Айталық,
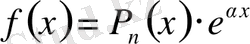 (4)
(4)
болсын, мұндағы
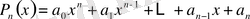 .
.
А) егер
 саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
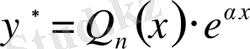 , (5)
, (5)
мұндағы
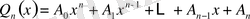 .
.
Б) егер
 саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
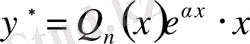 . (6)
. (6)
ІІІ. Айталық,
 болсын.
болсын.
А) егер
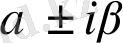 характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
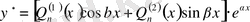
Б) егер
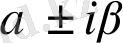 характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
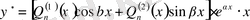 .
.
ІV. Айталық,
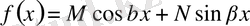 болсын, мұндағы
болсын, мұндағы
 мен
мен
 - тұрақтылар.
- тұрақтылар.
А) егер
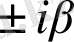 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
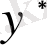 - ны мына түрде іздейміз:
- ны мына түрде іздейміз:
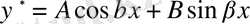 , мұндағы А мен В - белгісіз коэффици-енттер.
, мұндағы А мен В - белгісіз коэффици-енттер.
Б) егер
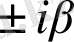 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
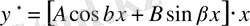 деп іздейміз.
деп іздейміз.
Мысал 1.
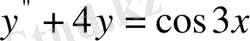 теңдеуін шеш.
теңдеуін шеш.
Шешу.
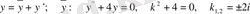 .
.
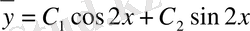 .
.
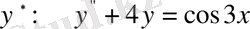
теңдеуінің кез келген бір дербес шешімі.
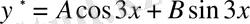 деп іздейміз.
деп іздейміз.
 .
.
Осыларды берілген теңдеуге апарып қоямыз. Сонда
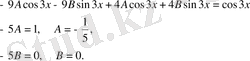
Бұдан
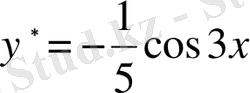 .
.
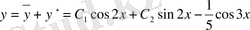 .
.
Мысал 2.
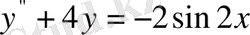 теңдеуін шеш.
теңдеуін шеш.
Шешу.
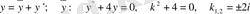 .
.
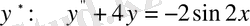
теңдеуінің кез келген бір дербес шешімі.
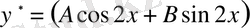 деп іздейміз.
деп іздейміз.
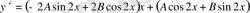

Осыларды берілген теңдеуге апарып қоямыз. Сонда

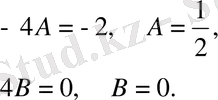
Бұдан
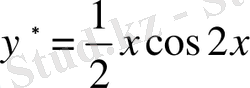 .
.
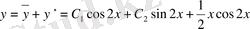 .
.
Мысал.
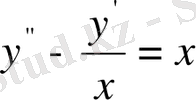 теңдеудің жалпы шешімін тап.
теңдеудің жалпы шешімін тап.
Шешу.
Алдымен мына біртекті теңдеудің жалпы шешімін табамыз.
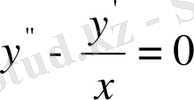 . Бұны
. Бұны
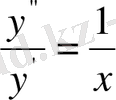 деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
деп жазып аламыз. Сонан соң оны интегралдасақ мынау шығады:
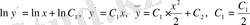 , яғни
, яғни
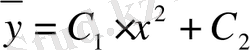 .
.
Бұл соңғы өрнек біртекті теңдеудің жалпы шешімі. Енді
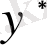 - ны іздейміз. Ал
- ны іздейміз. Ал
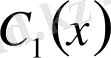 пен
пен
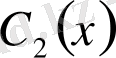 - ті мына жүйеден табамыз:
- ті мына жүйеден табамыз:
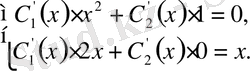
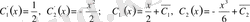 .
.
Егер бұл жерде
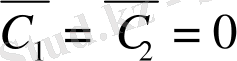 десек, онда
десек, онда
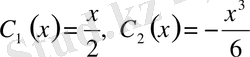 болады.
болады.
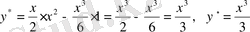 .
.
Енді тұрақты коэффициентті екінші ретті біртекті емес сызықтық диф-ференциалдық теңдеулерді қарастырамыз.
Анықтама. Тұрақты коэффициентті екінші ретті біртекті емес сызықтық
дифференциалдық теңдеу деп мына түрдегі
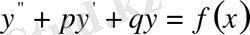 (1)
(1)
теңдеуді айтады, егер коэффициенттер
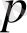 мен
мен
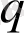 нақты сандар болса.
нақты сандар болса.
Мұның алдында біртекті емес теңдеудің дербес шешімін табатын жалпы әдіс көрсетіледі. Тұрақты коэффициентті біртекті емес теңдеулердің дербес шешімін табу кейбір дербес жағдайларда оңай жолмен шешіледі, яғни интегралдау амалын қолданбастан. Қазір (1) теңдеу үшін сондай жағдайлардың түрлерін қарастырамыз.
І. Айталық,
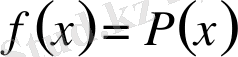 (2)
(2)
болсын, мұндағы
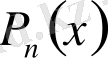 -
-
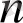 дәрежелі көпмүшелік, яғни
дәрежелі көпмүшелік, яғни
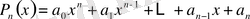 .
.
А) егер ноль саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
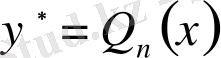 ,
,
яғни
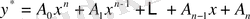 (3)
(3)
мұндағы
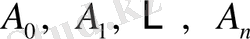 - уақытша белгісіз коэффициенттер.
- уақытша белгісіз коэффициенттер.
Б) егер ноль саны характеристикалық теңдеудің түбірі болма, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
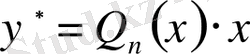 .
.
ІІ. Айталық,
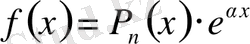 (4)
(4)
болсын, мұндағы
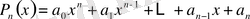 .
.
А) егер
 саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
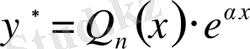 , (5)
, (5)
мұндағы
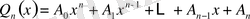 .
.
Б) егер
 саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
саны характеристикалық теңдеудің түбірі болса, онда дербес шешімді мына түрде іздейміз:
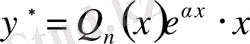 . (6)
. (6)
ІІІ. Айталық,
 болсын.
болсын.
А) егер
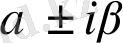 характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болмаса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
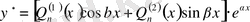
Б) егер
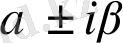 характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
характеристикалық теңдеудің түбірі болса, онда берілген біртекті емес теңдеудің дербес шешімін мына түрде іздейміз:
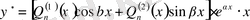 .
.
ІV. Айталық,
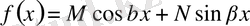 болсын, мұндағы
болсын, мұндағы
 мен
мен
 - тұрақтылар.
- тұрақтылар.
А) егер
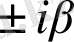 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
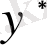 - ны мына түрде іздейміз:
- ны мына түрде іздейміз:
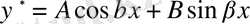 , мұндағы А мен В - белгісіз коэффици-енттер.
, мұндағы А мен В - белгісіз коэффици-енттер.
Б) егер
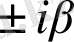 характеристикалық теңдеудің түбірі болмаса, онда
характеристикалық теңдеудің түбірі болмаса, онда
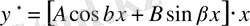 деп іздейміз.
деп іздейміз.
Мысал 1.
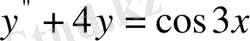 теңдеуін шеш.
теңдеуін шеш.
Шешу.
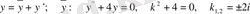 .
.
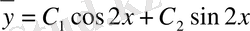 .
.
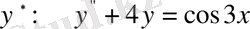
теңдеуінің кез келген бір дербес шешімі.
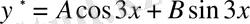 деп іздейміз.
деп іздейміз.
 .
.
Осыларды берілген теңдеуге апарып қоямыз. Сонда
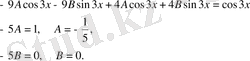
Бұдан
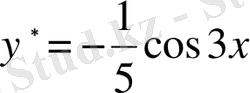 .
.
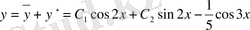 .
.
Мысал 2.
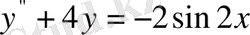 теңдеуін шеш.
теңдеуін шеш.
Шешу.
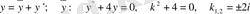 .
.
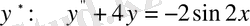
теңдеуінің кез келген бір дербес шешімі.
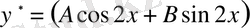 деп іздейміз.
деп іздейміз.
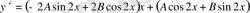

Осыларды берілген теңдеуге апарып қоямыз. Сонда

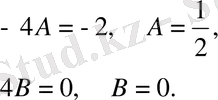
Бұдан
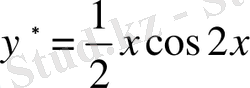 .
.
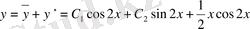 .
.
ІІ. Механикалық тербелістердің дифференциалдық теңдеулері.
1. Ерікті және ерікті емес тербелістердің дифференциалдық теңдеулері.
Бұл тарауда қолданбалы механиканың бір мәселесін қарастырамыз. Оны сызықтық дифференциалдық теңдеулердің көмегі арқылы зерттейміз және шешеміз.
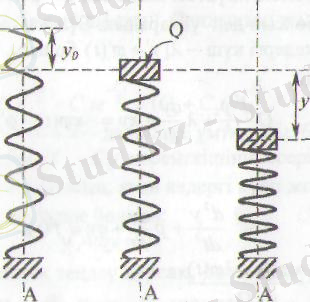
1-сурет
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz