Меншіксіз интегралдар: бірінші және екінші текті анықтамалар, жинақталу критерийлері және параметрге тәуелді интегралдар


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:
ПАПАЛЛЕЛ ИНТЕГРАЛ
МАЗМҰНЫ
Кіріспе . . .
I. Бірінші текті меншіксіз интегралдар. . . .
1. 1 Бірінші текті меншіксіз интеграл ұғымы . . .
1. 2 Меншіксіз интеграл мен қатар арасындағы сәйкестіктер . . .
1. 3 Меншіксіз интегралдың жинақтылық белгілері . . .
1. 4 Абель және Дирихле интегралдары . . .
II . Екінші текті меншіксіз интегралдар. . . .
2. 1 Екінші текті меншіксіз интеграл ұғымы . . .
2. 2 Интегралдық есептеудің негізгі формуласын қолдану . . .
2. 3 Меншіксіз интегралдың бар болуының шарттары мен
белгілері . . .
2. 4 Меншіксіз интегралдардың бас мәндері . . .
III . Меншіксіз интегралдардың параметрден тәуелді
болып келген жғадайлары . . .
3. 1 Меншіксіз интеграл параметрден тәуелді болған жағдайда
шекке көшу . . .
3. 2 Меншіксіз интеграл параметрден тәуелді болған жағдайда
дифференциалдау және интегралдау . . .
3. 3 Интегралдау шектеріде параметрден тәуелді интегралдар . . .
IV. Меншіксіз интегралдар параметрден тәуелді болған
жағдайда оларды кейбір интегралдарды есептеуде
қолданылуы . . .
4. 1 Меншіксіз интегралдар шектеріде параметрден тәуелді
болып келге жағдайлар . . .
4. 2 Меншіксіз интеграл белгісінің астында шекке көшу . . .
4. 3 Меншіксіз интегралды параметр бойынша интегралдау және
дифференциалдау . . .
4. 4 Кейбір меншіксіз интегралдарды есептеуге қолданылуы . . .
4. 5 Эйлердің біртекті және екітекті интегралдары . . .
4. 6 Эйлер интегралдарының көмегімен кейбір интегралдарды
есептеу . . .
Қорытынды . . .
Әдебиеттер . . .
4
5
5
13
14
17
23
23
26
27
32
38
38
40
44
47
47
48
49
51
54
59
62
63
КІРІСПЕ
Өзектілігі. Әдеттегі анықталған интегралдан өзгеше интегралдар да бар. Олар меншіксіз интегралдар деп аталады. меншіксіз интегралдар біртекті және екітекті болып, екі түрлі болады.
Біртекті меншіксіз интегралдар интегралдау шектері ақырсыз болып келген интегралдар, ал екітекті меншіксіз интегралдар интеграл астындағы функция интегралдау аралығының шеттерінде немесе оның ішінде шенелмеген болып келген интегралдар.
Жаңашылдығы. Бұндай интегралдардың мәндерін табу кейде мүмкін, кейде мүмкін емес болады. Егер мәні табылып, ол мән тиянақ-ты санға тең болса, онда меншіксіз интегралдың мәні сол мәнге тең бо-лады да, онда меншіксіз интегралды жинақталады деп айтамыз. Көпте-ген жағдайларда меншіксіз интегралдың мәнін табу мүмкін болмайды. Бұл жағдайда меншіксіз интегралдарды жинақталу белгісі арқылы жинақтылыққа зерттейді. Әр түрлі белгілер бар: салыстыру белгісі , Абель және Дирихле белгілері.
Проблемалық маңыздылығы. Көп өрнектерде параметр қатысқан болады, соның ішінде интегралдар да параметр қатысқан болады. Ол интегралдардан тікелей шек табу және интеграл табу өте қиын болады.
Мақсаты. Осындай жағдайларда ол өрнектерден алдымен параметр бойынша шекке көшсек, параметр бойынша туынды тапсақ немесе параметр бойынша интеграл тауып алып, кейін көрсетілген амалды орындасақ, онда әлдеқайда жеңіл болады.
Бұл жұмыс III және IV-тараулардан және қорытындыдан тұрады. III-тарауда үш параграф, ал IV-тарауда төрт параграф бар. Соңында әдебиеттер тізімі келтірілген.
Міндеті. Әрбір параграфтан кейін есептер шығарылып көрсетілген. IV- тараудың соңғы 4-ші параграфта тек есептер шығарылған.
Жұмыс төрт тараудан, кіріспеден және қорытындыдан тұрады. Соңында пайдаланған әдебиеттер тізімі келтірілген.
I. БІРІНШІ ТЕКТІ МЕНШІКСІЗ ИНТЕГРАЛДАР
1. 1 Бірінші текті меншіксіз интеграл ұғымы
Біз осы уақытқа дейін
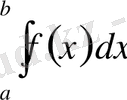 түріндегі интеграл ұғымын қарас-тырып келдік. Бірақ бұл интегралды қарастырғандла мынадай екі шарттың орындалуын талап еттік. Олар:
түріндегі интеграл ұғымын қарас-тырып келдік. Бірақ бұл интегралды қарастырғандла мынадай екі шарттың орындалуын талап еттік. Олар:
1.
 аралығы ақырлы аралық болсын.
аралығы ақырлы аралық болсын.
2.
 функциясы сол
функциясы сол
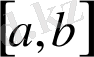 аралығында шенелген болсын.
аралығында шенелген болсын.
Біз бұл I тарауда жоғарыдағы екі шарттың бірінші шарты сақталмаған жағдайды қарастырамыз.
Айталық
 функциясы
функциясы
 аралығында анықталған болсын, яғни
аралығында анықталған болсын, яғни
 үшін анықталған болсын және ол аралықтың кез келген ақырлы бөлігі
үшін анықталған болсын және ол аралықтың кез келген ақырлы бөлігі
 аралығында интегралданатын болсын. Бұл деген сөз
аралығында интегралданатын болсын. Бұл деген сөз
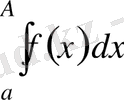 интегралы
интегралы
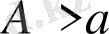 болғанда мағынаға ие деген сөз.
болғанда мағынаға ие деген сөз.
Анықтама.
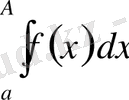 интегралының
интегралының
 - дағы шегі
- дағы шегі
 функция-сының
функция-сының
 - дан
- дан
 ке дейін алынған интегралы деп атайды және оны мына символмен белгілейді:
ке дейін алынған интегралы деп атайды және оны мына символмен белгілейді:
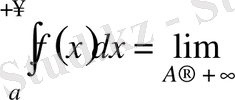
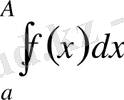 . (1)
. (1)
Егер бұл шек ақырлы болса, онда (1) интеграл жинақталады деп аталады ал
 функциясын
функциясын
 ақырсыз аралығында интеграл-данады деп атайды. Егер де (1) шек ақырсыз немесе мүлде жоқ болса, онда (1) интеграл жинақталмайды деп аталады.
ақырсыз аралығында интеграл-данады деп атайды. Егер де (1) шек ақырсыз немесе мүлде жоқ болса, онда (1) интеграл жинақталмайды деп аталады.
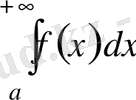 интегралы бұрын қарастырған.
интегралы бұрын қарастырған.
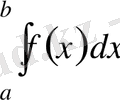 интегралынан ажы-ратып айту үшін бірінші текті меншіксіз интеграл деп атайды, ал
интегралынан ажы-ратып айту үшін бірінші текті меншіксіз интеграл деп атайды, ал
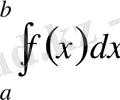 интегралын меншікті интеграл немесе анықталған интеграл деп атайды.
интегралын меншікті интеграл немесе анықталған интеграл деп атайды.
Анықтама.
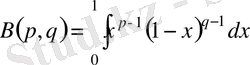 (1) түріндегі интеграл Эйлердің 1 - текті интегралы немесе екі айнымалы
(1) түріндегі интеграл Эйлердің 1 - текті интегралы немесе екі айнымалы
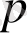 мен
мен
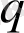 - дың «Бета - функциясы» деп аталады.
- дың «Бета - функциясы» деп аталады.
Эйлердің бірінші текті интегралының қасиеттері:
1)
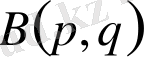 функциясының жинақталыс облысы
функциясының жинақталыс облысы
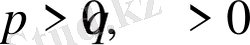 болады. Шынында, (1) интеграл екі интегралдың қосындысы түрінде былай өрнектеледі:
болады. Шынында, (1) интеграл екі интегралдың қосындысы түрінде былай өрнектеледі:
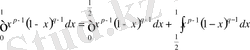 .
.
Шек
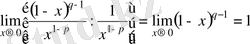 .
.
Сондықтан интеграл
 ,
,
 болғанда жинақталады.
болғанда жинақталады.
Сонымен бірге
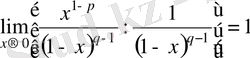 болуы себепті, интеграл
болуы себепті, интеграл
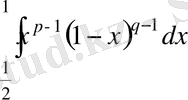
 болғанда жинақталады.
болғанда жинақталады.
2) Бета - функция
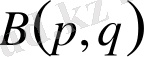 өзінің аргументтері
өзінің аргументтері
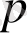 мен
мен
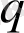 бойынша сим-метриялы.
бойынша сим-метриялы.
Шынында, егер
 ауыстырмасын енгізсек, онда
ауыстырмасын енгізсек, онда
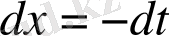 ,
,
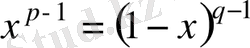 және
және
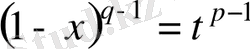 . Сонда:
. Сонда:
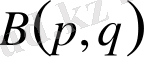
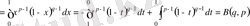
- функцияөзінің жинақталу облысының кез келген нүктесінде үзіліссіз.
- Функцияүшін келтіру формуласы деп аталатын натурал саныүшін
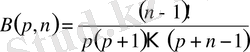 (2)
(2)
формуласы орынды.
Дәлелдеу.
Егер
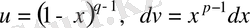 ауыстырмасын енгізіп, сонан кейін
ауыстырмасын енгізіп, сонан кейін
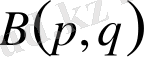 интегралын бөліктеп интегралдау жолымен есептесек,
интегралын бөліктеп интегралдау жолымен есептесек,
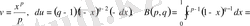
 (3)
(3)
болады.
Осы (3) теңдіктің оң жағындағы интегралды (1) интегралмен салыстырсақ,
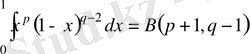 екенін көреміз. Демек,
екенін көреміз. Демек,
(4)
Соңғы (4) теңдіктегі
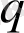 - ды натурал сан
- ды натурал сан
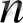 - мен ауыстырсақ,
- мен ауыстырсақ,
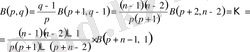 (5) формуласына келеміз. Ал
(5) формуласына келеміз. Ал
(6)
Ендеше (5) мен (6) теңдіктерден
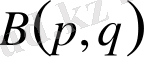 функциясы үшін (2) келтіру формуласының әділдігі шығады.
функциясы үшін (2) келтіру формуласының әділдігі шығады.
Эйлердің бірінші текті интегралы (1) -ні екінші түрде де жазуға болады. Ол үшін
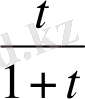 ауыстырмасын енгіземіз. Сонда
ауыстырмасын енгіземіз. Сонда
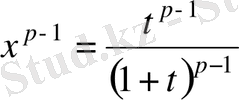 ,
,
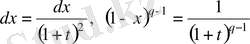 болады да, (1) интеграл мына түрге келеді:
болады да, (1) интеграл мына түрге келеді:
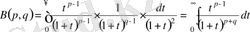 . (7)
. (7)
Егер (7) формулада
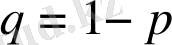 деп алсақ,
деп алсақ,
 болып шығады. Ал
болып шығады. Ал
 екені белгілі. Демек,
екені белгілі. Демек,
 ,
,
 . (8)
. (8)
Егер (8) формулада
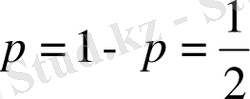 деп алсақ,
деп алсақ,
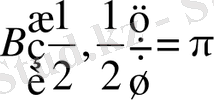 болады.
болады.
Анықтама.
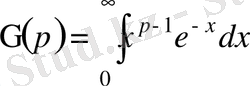 (9) түріндегі интеграл Эйлердің екінші текті интегралы немесе «Гамма - функция» деп аталады.
(9) түріндегі интеграл Эйлердің екінші текті интегралы немесе «Гамма - функция» деп аталады.
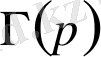 функцияның қасиеттері:
функцияның қасиеттері:
А) ол барлық
 мәндерінде жинақталады.
мәндерінде жинақталады.
Б) барлық
 үшін үзіліссіз функция.
үшін үзіліссіз функция.
В)
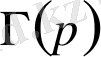 функциясы үшін мынадай келтіру формуласы орындалады.
функциясы үшін мынадай келтіру формуласы орындалады.
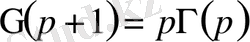 (10)
(10)
Дәлелдеу.
Егер (9) интегралдағы
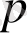 - ның орнына
- ның орнына
 - ді алсақ,
- ді алсақ,
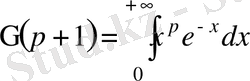 (11) болады. Сонан соң
(11) болады. Сонан соң
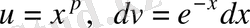 деп белгілеп, (11) интегралды бөліктеп интегралдасақ,
деп белгілеп, (11) интегралды бөліктеп интегралдасақ,
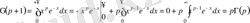 теңдігіне келеміз.
теңдігіне келеміз.
Егер
 (
(
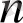 - натурал сан) деп алсақ,
- натурал сан) деп алсақ,
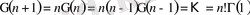
болар еді.
Ал
 екенін ескерсек,
екенін ескерсек,
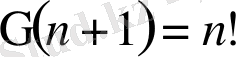 формуласы шыға-ды.
формуласы шыға-ды.
2) Эйлер интегралдары
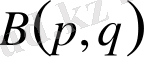 мен
мен
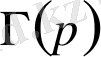 - нің арасында мынадай байланыс бар:
- нің арасында мынадай байланыс бар:
 (12)
(12)
Дәлелдеу.
(9) интегралда
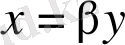 (
(
 нақты сан) ауыстырмасын енгізсек,
нақты сан) ауыстырмасын енгізсек,
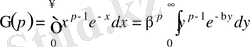
түріне келеді. Соңғы теңдікте
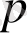 - ні
- ні
 мен,
мен,
 -ні
-ні
 -мен ауыстырсақ,
-мен ауыстырсақ,
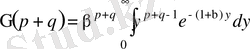
немесе
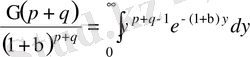 (13) болады. бұл теңдіктің екі жағын да
(13) болады. бұл теңдіктің екі жағын да
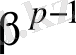 - ге көбейтіп, шыққан теңдікті
- ге көбейтіп, шыққан теңдікті
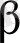 бойынша интегралдағанда
бойынша интегралдағанда
 (14) болады. Ал
(14) болады. Ал
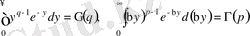
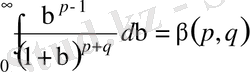 ((7) формула бойынша) .
((7) формула бойынша) .
Демек, (14) теңдік мына түрге келеді:
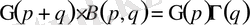 ,
,
яғни (12) формула әділ.
Д) Гамма - функция
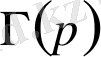 үшін Эйлер - Гаусс формуласы
үшін Эйлер - Гаусс формуласы
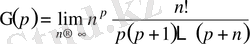 (15) орындалады.
(15) орындалады.
Е) егер (12) формулада
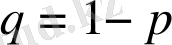 деп алып, (8) формуланы және
деп алып, (8) формуланы және
 екенін ескерсек,
екенін ескерсек,
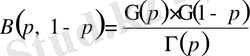 , яғни толықтыру формуласы деп аталатын
, яғни толықтыру формуласы деп аталатын
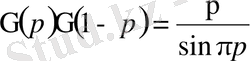 (16) формуласына келеміз.
(16) формуласына келеміз.
Мысалдар.
1.
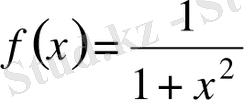 функциясы кез келген
функциясы кез келген

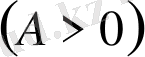 ақырлы аралығында интегралданады, сонымен бірге мынаған ие боламыз
ақырлы аралығында интегралданады, сонымен бірге мынаған ие боламыз
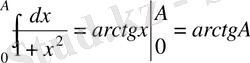 .
.
Бұл интеграл үшін
 - да ақырлы шек
- да ақырлы шек
 бар. Онда 0 - ден
бар. Онда 0 - ден
 - ке дейін интеграл жинақталады және оның мәні
- ке дейін интеграл жинақталады және оның мәні
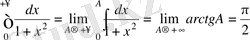 .
.
2.
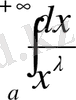
 (2) меншіксіз интегралы
(2) меншіксіз интегралы
 - нің қандай мәндерінде бар болады, соны зерттелік.
- нің қандай мәндерінде бар болады, соны зерттелік.
Айталық
 болсын. Онда
болсын. Онда
 .
.

Егер
 болса, онда
болса, онда
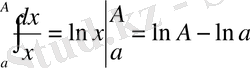 және
және
 - да бұның шегі
- да бұның шегі
 - ке тең болады.
- ке тең болады.
Сонымен (2) интеграл
 болғанда жинақталады да, мәні
болғанда жинақталады да, мәні
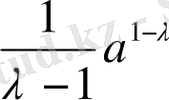 - ге тең болады, ал
- ге тең болады, ал
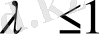 болғанда жинақталмайды.
болғанда жинақталмайды.
(1) - ге ұқсас
 функциясының
функциясының
 - тен
- тен
 - ға дейін алынған интегралы да анықталады, яғни:
- ға дейін алынған интегралы да анықталады, яғни:

 (3) және
(3) және
 функциясының
функциясының
 - тен
- тен
 - ке дейін алынған интегралы да анықталады, яғни:
- ке дейін алынған интегралы да анықталады, яғни:
 .
.
Соңғы анықталаған интегралдар да меншіксіз интегралдар деп аталады.
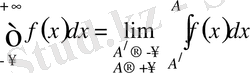 интеграл жағдайында кез келген
интеграл жағдайында кез келген
 -ні алып, былай жазуға болады
-ні алып, былай жазуға болады
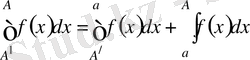 .
.
Бұл теңдеудің сол жағындағы интегралдың
 ,
,
 болғанда да бар болуы (1) мен (3) шектердің күн бұрын бар болуымен, яғни (1) мен (3) интегралдардың бар болуымен тең күшті. Сонымен,
болғанда да бар болуы (1) мен (3) шектердің күн бұрын бар болуымен, яғни (1) мен (3) интегралдардың бар болуымен тең күшті. Сонымен,
 - тен
- тен
 - ке дейінгі интегралды мынадай теңдікпен анықтауға болады
- ке дейінгі интегралды мынадай теңдікпен анықтауға болады
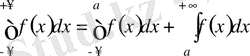 .
.
Мысалдар.
1.
 .
.
2.
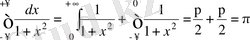 .
.
Сөйтіп, біз жоғарыда меншіксіз интегралдардың мәнін есептеу үшін алдымен оның ақырлы аралық үшін алғашқы функциясын тауып алып, кейін шекке көшу амалын қолдандық. Олай болса осы екі жағдайды біріктіріп жіберуге болады.
Айталық, мысалы,
 функциясы
функциясы
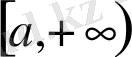 аралығында анықталған және
аралығында анықталған және
 аралығының әрбір ақырлы
аралығының әрбір ақырлы
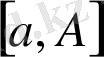 аралығында интеграл-данатын болсын. Егер
аралығында интеграл-данатын болсын. Егер
 функциясы үшін бүкіл
функциясы үшін бүкіл
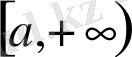 аралығында алғашқы функция
аралығында алғашқы функция
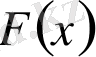 бар болса, онда интегралдық есептеудің негізгі формуласы былай жазуға болады
бар болса, онда интегралдық есептеудің негізгі формуласы былай жазуға болады
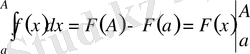 .
.
Бұдан көрініп тұр, (1) меншіксіз интеграл бар болады сонда, тек сонда, егер мына ақырлы шек бар болса
 ,
,
және
 .
.
Дәл осы сияқты
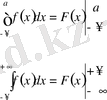
бұл жерде
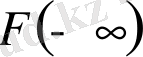 арқылы
арқылы
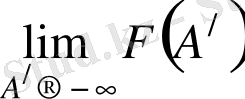 шегін түсіну керек.
шегін түсіну керек.
Мысалдар. 1.
 меншщіксіз интегралын есептеу керек.
меншщіксіз интегралын есептеу керек.
Шешу.

2.
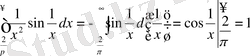
3.
 гиперболасының
гиперболасының
 тармағы
тармағы
 осінен айналады. Сонда пайда болған айналу денесінің көлемі мен бетін есепте.
осінен айналады. Сонда пайда болған айналу денесінің көлемі мен бетін есепте.
Шешу.
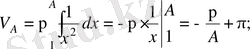
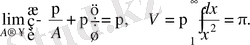
 .
.
Бұдан
 - да
- да
 , яғни көлем ақырлы санға тең де, беті шексізге тең.
, яғни көлем ақырлы санға тең де, беті шексізге тең.
1. 2 Меншіксіз интеграл мен қатар арасындағы сәйкестіктер
Біз бұл жерде тек (1) түріндегі меншіксіз интегралды қарастырумен шектелеміз, себебі бұл (1) үшін орынды қасиеттер (2) мен (3) үшін де орынды бола береді. Бұл жерде
 функциясы барлық уақытта
функциясы барлық уақытта
 мен
мен
 шектері арасында меншікті түрде интегралданады деп ұйғарамыз.
шектері арасында меншікті түрде интегралданады деп ұйғарамыз.
Сонымен
 меншіксіз интегралы мен
меншіксіз интегралы мен
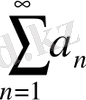 қатарының арасында өте көп ұқсастық бар.
қатарының арасында өте көп ұқсастық бар.
Егер
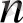 бойынша қосындылау процесін
бойынша қосындылау процесін
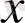 бойынша интегралдау процесімен алмастырсақ, онда мынадай ұқсастықтар шығады:
бойынша интегралдау процесімен алмастырсақ, онда мынадай ұқсастықтар шығады:
1.
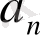 - қатардың жалпы мүшесі
- қатардың жалпы мүшесі
 - интеграл астындағы функция
- интеграл астындағы функция
2.
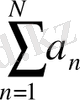 - қатардың дербес қосындысы
- қатардың дербес қосындысы
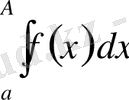 - меншікті интеграл
- меншікті интеграл
3.
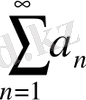 - қатардың қосындысы (дербес қосындының шегі ретінде)
- қатардың қосындысы (дербес қосындының шегі ретінде)
 - меншіксіз интеграл (алдыңғы интегралдың
- меншіксіз интеграл (алдыңғы интегралдың
 - дағы шегі
- дағы шегі
ретінде) .
4.
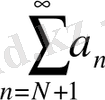 - қатардың қалдығы
- қатардың қалдығы
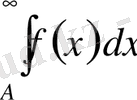 - интеграл.
- интеграл.
Қатарлар туралы теоремаларға ұқсас меншіксіз интегралдар туралы мына теоремаларды келтіреміз.
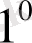 . Егер
. Егер
 интегралы жинақталса, онда
интегралы жинақталса, онда
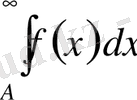 (
(
 ) интег-ралы да жинақталады, және керісінше. Сонда
) интег-ралы да жинақталады, және керісінше. Сонда
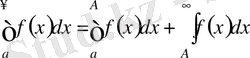 .
.
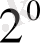 .
.
 интегралы жинақты болған жағдайда мынаған келеміз:
интегралы жинақты болған жағдайда мынаған келеміз:
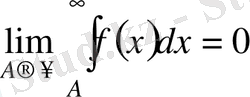 .
.
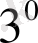 .
.
 интегралының жинақтылығынан
интегралының жинақтылығынан

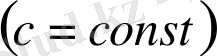 интегралының жинақтылығы шығады, сонымен бірге
интегралының жинақтылығы шығады, сонымен бірге
 .
.
 . Егер
. Егер
 және
және
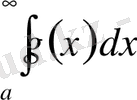 интегралдарының екеуі де жинақты болса, онда
интегралдарының екеуі де жинақты болса, онда
 интегралы да жинақты болады және
интегралы да жинақты болады және


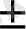
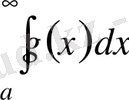 .
.
1. 3 Меншіксіз интегралдың жинақтылық белгілері
Егер
 функциясы оң (теріс емес) болса, онда
функциясы оң (теріс емес) болса, онда

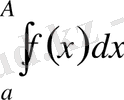 (4) интегралы бірсарынды өспелі функцияны береді, яғни айнымалы
(4) интегралы бірсарынды өспелі функцияны береді, яғни айнымалы
 - ның бірсарынды функциясын береді. Оның
- ның бірсарынды функциясын береді. Оның
 - да ақырлы шегі бар болуы бірсарынлды функцияның шегі бар болуы туралы теоремадан белгілі, яғни:
- да ақырлы шегі бар болуы бірсарынлды функцияның шегі бар болуы туралы теоремадан белгілі, яғни:
(1) меншіксіз интегралдың
 функциясы оң болған жағдайда жинақты болуы үшін (4) интеграл А өскенде жоғарыдан шенелген болуы, яғни
функциясы оң болған жағдайда жинақты болуы үшін (4) интеграл А өскенде жоғарыдан шенелген болуы, яғни


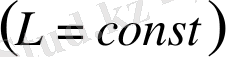
болуы қажет және жеткілікті.
Егер де бұл шарт орындалмаса, онда (1) интегралдың мәні
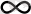 - ке тең.
- ке тең.
Осы тұжырымға мына теорема (салыстыру теоремасы) негізделген.
Теорема 1.
Егер ең болмағанда
 болғанда мына теңсіздік
болғанда мына теңсіздік
 орынды болса, онда
орынды болса, онда
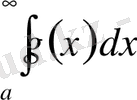 интегралының жинақтылығынан
интегралының жинақтылығынан
 интегралының жинақтылығы келіп шығады, немесе,
интегралының жинақтылығы келіп шығады, немесе,
 интегралының жинақсыздығынан
интегралының жинақсыздығынан
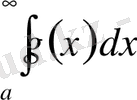 интегралының жинақсыздығы келіп шығады.
интегралының жинақсыздығы келіп шығады.
Бұл теореманы дәлелдеу үшін қатарлардың жинақтылығының салыстыру теоремасын сөзбе - сөз көшірсе болғаны.
Теорема 2. Егер мына шек
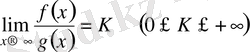 бар болса, онда
бар болса, онда
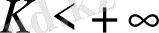 болғанда
болғанда
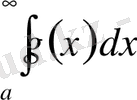 интегралының жинақтылығынан
интегралының жинақтылығынан
 интегралының жинақтылығы келіп шығады, ал
интегралының жинақтылығы келіп шығады, ал
 болғанда
болғанда
 интегралының жинақсыздығынан
интегралының жинақсыздығынан
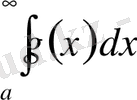 интегралының жинақ-сыздығы келіп шығады.
интегралының жинақ-сыздығы келіп шығады.
Сөйтіп,
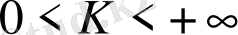 болғанда екі интеграл не бір уақытта жинақталады, не бір уақытта жинақталмайды.
болғанда екі интеграл не бір уақытта жинақталады, не бір уақытта жинақталмайды.
Бұл теореманың да дәлелдемесі қатардағы теореманың дәлелдемесіне ұқсас.
Салыстыру үшін тиянақты функцияны таңдап алып,
 интег-ралының жинақтылығын немесе жинақсыздығын анықтайтын дербес белгілер табуға болады. Практикада
интег-ралының жинақтылығын немесе жинақсыздығын анықтайтын дербес белгілер табуға болады. Практикада
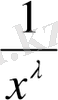 функциясымен салыстыру жиі қолданылады, яғни
функциясымен салыстыру жиі қолданылады, яғни
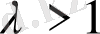 болғанда бұл функция интегралданады (
болғанда бұл функция интегралданады (
 - дан
- дан
 - ке дейін алынған интеграл үшін), ал
- ке дейін алынған интеграл үшін), ал
 болғанда интегралданбайды.
болғанда интегралданбайды.
Айталық
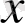 - тің жеткілікті үлкен мәндері үшін
- тің жеткілікті үлкен мәндері үшін
 функциясы мынадай түрге ие болсын
функциясы мынадай түрге ие болсын

 .
.
Онда: 1) егер
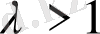 және
және
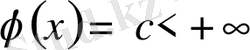 болса, онда
болса, онда
 жинақталады,
жинақталады,
2) егер де
 және
және
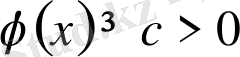 болса, онда
болса, онда
 интеграл жинақталмайды.
интеграл жинақталмайды.
Бұл теореманы дәлелдеу үшін 1-теореманы пайдалану керек; салыс-тыру функциясы
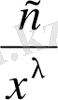 функциясы болып табылады.
функциясы болып табылады.
Егер
 - да
- да
 функциясы реті
функциясы реті
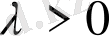 - ге тең ақырсыз кішкене болып табылса (
- ге тең ақырсыз кішкене болып табылса (
 пен салыстырғанда), онда
пен салыстырғанда), онда
 итеграл
итеграл
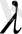 - ның мәніне байланысты жинақты немесе жинақсыз болады, яғни
- ның мәніне байланысты жинақты немесе жинақсыз болады, яғни
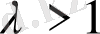 болғанда жинақты, ал
болғанда жинақты, ал
 болғанда жинақсыз болады.
болғанда жинақсыз болады.
Бұл жерде 2 -теоремаға жүгіну керек.
 функциясының ролін
функциясының ролін
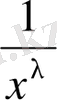 функциясы атқарады.
функциясы атқарады.
Мысалдар.
1.
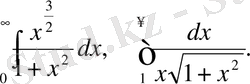
Бұл интегралдардағы интеграл астындағы функциялар ақырсыз кіш-кене функциялар реттері сәйкесінше
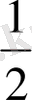 және 2 тең. Сондықтан бірінші интеграл жинақталмайды, ал екінші интеграл жинақталады.
және 2 тең. Сондықтан бірінші интеграл жинақталмайды, ал екінші интеграл жинақталады.
Енді меншіксіз интегралдың жинақтылығынан жалпы жағдайда қарастырамыз.
 меншіксіз интегралдың бар болуы туралы мәселе, (1) -дің анықтамасына сәйкес,
меншіксіз интегралдың бар болуы туралы мәселе, (1) -дің анықтамасына сәйкес,
 - да мына функцияның
- да мына функцияның

 (4) шегінің ақырлы болуына келіп тіреледі.
(4) шегінің ақырлы болуына келіп тіреледі.
Осы функцияға Больцано-Коши белгісін қолданып, меншіксіз интегралдың бар болуын шартын мына түрде айтуға болады:
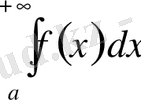 меншщіксіз интегралының жинақталуы үшін кез келген
меншщіксіз интегралының жинақталуы үшін кез келген
 үшін сондай
үшін сондай
 саны табылып,
саны табылып,
 және
және
 болғанда мына теңсіздіктің орындалуы
болғанда мына теңсіздіктің орындалуы
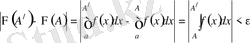 қажет және жеткілікті.
қажет және жеткілікті.
Бұл критерий оңай ғана мына тұжырымды алып келеді:
Егер интеграл
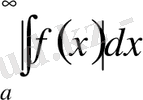 жинақталса, онда интегралы
жинақталса, онда интегралы
 одан да бетер жинақталады.
одан да бетер жинақталады.
Шынында, жоғарыдағы критерийді
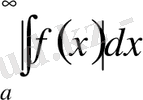 интегралына қолданып және оның жинақтылығын ескеріп, мынаған келеміз: кез келген
интегралына қолданып және оның жинақтылығын ескеріп, мынаған келеміз: кез келген
 үшін
үшін
 саны табылып, тек
саны табылып, тек
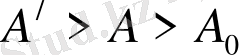 болғанда
болғанда
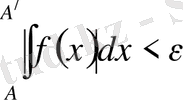 болады. Мынадай болатыны анық (белгілі)
болады. Мынадай болатыны анық (белгілі)
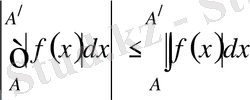 .
.
Олай болса
 . Бұдан келіп шығады
. Бұдан келіп шығады
 интегралының жинақтылығы.
интегралының жинақтылығы.
Мынаны ескеру керек:
 интегралының жинақталуынан, жалпы жағдайда,
интегралының жинақталуынан, жалпы жағдайда,
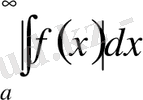 интегралының жинақтылығы шықпайды. Егер
интегралының жинақтылығы шықпайды. Егер
 интегралымен қатар
интегралымен қатар
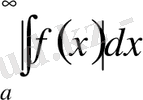 интегралы да жинақталатын болса, онда
интегралы да жинақталатын болса, онда
 интегралы абсолют жинақталатын болса, онда
интегралы абсолют жинақталатын болса, онда
 интегралы абсолют жинақталатын деп аталады, ал
интегралы абсолют жинақталатын деп аталады, ал
 функциясын абсолют интегралданатын функция деп атайды (
функциясын абсолют интегралданатын функция деп атайды (
 аралығында) . Абсолют емес жинақталатын интегралға мысалды сәл кейін келтіреміз.
аралығында) . Абсолют емес жинақталатын интегралға мысалды сәл кейін келтіреміз.
Таңбасы айнымалы
 функциясы үшін жоғарыдағы белгілер қолданылмайды. Бірақ
функциясы үшін жоғарыдағы белгілер қолданылмайды. Бірақ
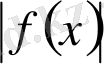 функциясы үшін ол белгілерді қолдануға болады.
функциясы үшін ол белгілерді қолдануға болады.
Бұдан келесі тұжырым келіп шығады және бұл жиі пайдалы болады:
Егер
 функциясы
функциясы
 аралығында абсолют интегралданса, ал
аралығында абсолют интегралданса, ал
 функциясы шенелген болса, онда олардың көбейтіндісі
функциясы шенелген болса, онда олардың көбейтіндісі
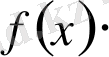
 те
те
 аралығында абсолют интегралданатын болады.
аралығында абсолют интегралданатын болады.
Бұл тұжырымды дәлелдеу үшін мына теңсіздікке жүгінсек жеткілікті:
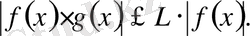
Мысал.
 интегралы берілген. Бұл жерде
интегралы берілген. Бұл жерде
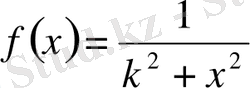 функциясы (абсолют) интегралданады, ал
функциясы (абсолют) интегралданады, ал
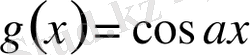 функциясы, көрініп тұр, шенелген. Бұдан келіп шығады берілген интеграл абсолют жинақ-талады.
функциясы, көрініп тұр, шенелген. Бұдан келіп шығады берілген интеграл абсолют жинақ-талады.
1. 4 Абель және Дирихле интегралдары
Біз бұл жерде басқа типтегі белгілерді келтіреміз. Бұл белгілер орта мән туралы теоремалардың екінші теоремасына негізделген. Олар шексіз қатарлардың жинақтылығының Абель және Дирихле белгілеріне ұқсас.
Абель белгісі.
Айталық
 және
және
 функциялары
функциялары
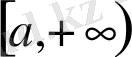 аралы-ғында анықталған, сонымен бірге
аралы-ғында анықталған, сонымен бірге
1)
 функциясы ол аралықта интегралданады, демек,
функциясы ол аралықта интегралданады, демек,
(1) интеграл жинақталады.
2)
 функциясы бірсарынды және шенелген, яғни:
функциясы бірсарынды және шенелген, яғни:

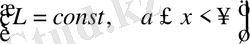 , онда
, онда
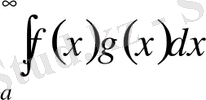 (5)
(5)
жинақталады.
Дәлелдеу.
Орта мән туралы екінші теорема бойынша кез келген
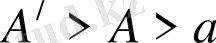 үшін мынау болады
үшін мынау болады
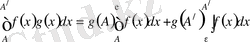 , (6)
, (6)
бұндағы
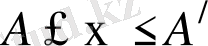 . 1) шарт бойынша, яғни (1) интегралға қойылған шарт бойынша кез келген
. 1) шарт бойынша, яғни (1) интегралға қойылған шарт бойынша кез келген
 үшін сондай
үшін сондай
 табылып,
табылып,
 болғанда мынау болады
болғанда мынау болады

Ал енді 2) шарт бойынша
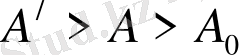 болғанда мынау болады
болғанда мынау болады
 .
.
Бұдан (5) интегралдың жинақтылығы келіп шығады.
Дирихле белгісі. Айталық
1)
 функциясы кез келген ақырлы
функциясы кез келген ақырлы
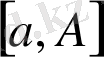
 аралығында интегралданады және (4) интеграл шенелген болатын болсын
аралығында интегралданады және (4) интеграл шенелген болатын болсын

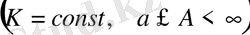 ,
,
2)
 функциясы
функциясы
 - да бірсарынды нольге ұмтылатын болсын, яғни:
- да бірсарынды нольге ұмтылатын болсын, яғни:
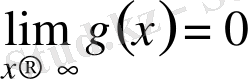 ,
,
онда (5) интеграл жинақталады.
Дәлелдеу.
Бұл белгінің дәлелдемесі жоғарыдағыдай жүргізіледі, яғни (6) теңдіктен келіп шығады. Бірақ бұл жерде
 мен
мен
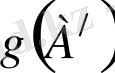 көбейткіштері жеткілікті аз болуы мүмкін, ал екінші көбейткіштер
көбейткіштері жеткілікті аз болуы мүмкін, ал екінші көбейткіштер
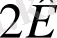 санымен шенелген.
санымен шенелген.
Мысал.
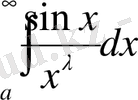 және
және
 инт егралдары
инт егралдары
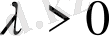 болғанда жинақталады.
болғанда жинақталады.
Дирихле белгісін пайдаланып, біз мынаған келеміз:
 немесе
немесе
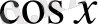 деп ұйғарамыз, ал
деп ұйғарамыз, ал
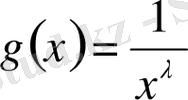 . Бұл жерде 1) шарттар орындалып тұр, яғни
. Бұл жерде 1) шарттар орындалып тұр, яғни
 және
және
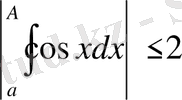 , ал
, ал
 функция
функция
 - да нольге ұмтылады.
- да нольге ұмтылады.
Бұдан
 болған дербес жағдайда мына интегралдың жинақтылығы келіп шығады
болған дербес жағдайда мына интегралдың жинақтылығы келіп шығады
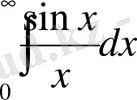 .
.
Біз бұл жерде
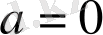 деп алуымызға болады, өйткені интеграл астындағы функция
деп алуымызға болады, өйткені интеграл астындағы функция
 да ақырлы шекке ие. Мынаны көрсетуге болады: жоғарыдағы интеграл абсолют емес жинақталады, яғни мына интеграл
да ақырлы шекке ие. Мынаны көрсетуге болады: жоғарыдағы интеграл абсолют емес жинақталады, яғни мына интеграл
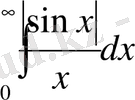 жинақталмайды. Шынында, егер де бұл интеграл жинақталатын болса, онда салысьыру теоремасы бойынша
жинақталмайды. Шынында, егер де бұл интеграл жинақталатын болса, онда салысьыру теоремасы бойынша
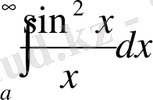

интеграл да жинақталады, өйткені
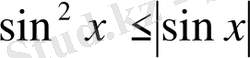 . Басқаша айтқанда
. Басқаша айтқанда
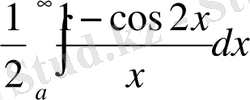 интегралы да жинақталады. Бұл соңғы интегралға жинақтылығы алдынан белгілі мына интегралды
интегралы да жинақталады. Бұл соңғы интегралға жинақтылығы алдынан белгілі мына интегралды
 қоссақ, онда мынадай қорытындыға келеміз:
қоссақ, онда мынадай қорытындыға келеміз:
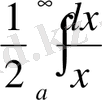 интегралы да жинақты болған болар еді. Бірақ олай емес, яғни
интегралы да жинақты болған болар еді. Бірақ олай емес, яғни
 интегралы жинақсыз.
интегралы жинақсыз.
Мына меншіксіз интегралдарды есепте.
2342 (Д) .

Есептеу.
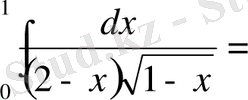 бұл жерде
бұл жерде
 ерекше нүкте =
ерекше нүкте =

2343 (Д) .

Есептеу.

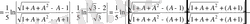
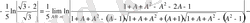

2344 (Д) .
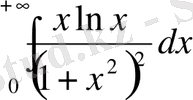
Есептеу.

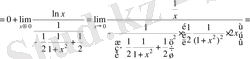

2357 (Д) . Мына шектерді тап:
А)

Б)

В)

Г)

II. ЕКІНШІ ТЕКТІ МЕНШІКСІЗ ИНТЕГРАЛДАР
2. 1 Екінші текті меншіксіз интеграл ұғымы
Бұл жерде
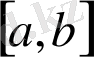 ақырлы аралығында берілген
ақырлы аралығында берілген
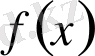 функциясын қарастырамыз, бірақ
функциясын қарастырамыз, бірақ
 бұл аралықта шенелмеген. Анығырақ айтқанда
бұл аралықта шенелмеген. Анығырақ айтқанда
 функциясы кез келген
функциясы кез келген
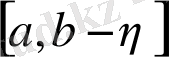
 аралығында шенелген және интегралданады, бірақ әрбір
аралығында шенелген және интегралданады, бірақ әрбір
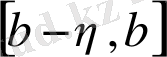 аралығында шенелмеген, яғни
аралығында шенелмеген, яғни
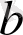 нүктесінің сол жағында шенелмеген. Бұл жағдайда
нүктесінің сол жағында шенелмеген. Бұл жағдайда
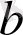 нүктесі
нүктесі
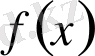 функциясының ерекше нүктесі деген атқа ие.
функциясының ерекше нүктесі деген атқа ие.
Анықтама.
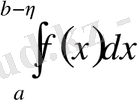 интегралының
интегралының
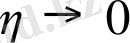 дағы шегі
дағы шегі
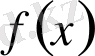 функция-сының
функция-сының
 - дан
- дан
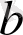 - ға дейін алынған меншіксіз интегралы деп аталады және оны былай белгілейді:
- ға дейін алынған меншіксіз интегралы деп аталады және оны былай белгілейді:

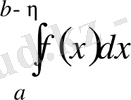 . (1)
. (1)
Егер бұл шек ақырлы болған жағдайда (1) интеграл жинақталады деп айтылады, ал
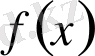 функциясын
функциясын
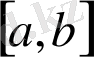 аралығында интегралданады деп атайды. Егер де (1) шек ақырсыз болса немесе мүлде жоқ болса, онда (1) интеграл жинақталмайды деп аталады.
аралығында интегралданады деп атайды. Егер де (1) шек ақырсыз болса немесе мүлде жоқ болса, онда (1) интеграл жинақталмайды деп аталады.
Мысал.
1)
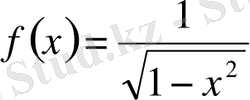 функциясы кез келген
функциясы кез келген
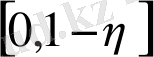
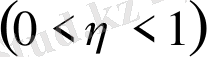 аралығында шенелген және интегралданады, сонымен бірге
аралығында шенелген және интегралданады, сонымен бірге
 .
.
 нүктесінде
нүктесінде
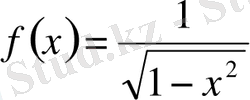 функциясы шексіздікке айналады. Бұл деген сөз
функциясы шексіздікке айналады. Бұл деген сөз
 - да
- да
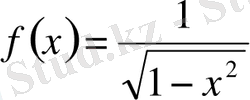 функциясы шексіздікке ұмтылады. Көрініп тұр кез келген
функциясы шексіздікке ұмтылады. Көрініп тұр кез келген
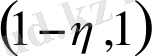 аралығында
аралығында
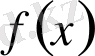 функциясы шенелмеген, яғни
функциясы шенелмеген, яғни
 нүктесі
нүктесі
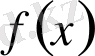 функциясының ерекше нүктесі болып табылады. Практикада осындай текті ерекше нүктелермен жұмыс істеуге тура келеді.
функциясының ерекше нүктесі болып табылады. Практикада осындай текті ерекше нүктелермен жұмыс істеуге тура келеді.
Сөйтіп, жоғарыдағы есептелген интеграл
 - да
- да
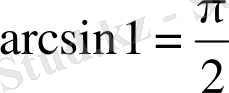 шегіне ұмтылады. Онда
шегіне ұмтылады. Онда

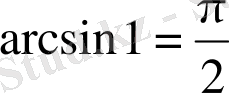 .
.
Айталық енді
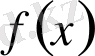 функциясы кез келген
функциясы кез келген

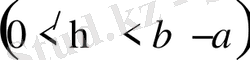 аралығында шенелген және интегралданатын болсын, бірақ әрбір
аралығында шенелген және интегралданатын болсын, бірақ әрбір
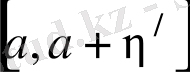 аралығында
аралығында
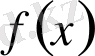 функциясы шенелмеген болып табылады, яғни
функциясы шенелмеген болып табылады, яғни
 нүктесінің оң жағында
нүктесінің оң жағында
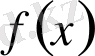 функциясы шенелмеген. Демек,
функциясы шенелмеген. Демек,
 нүктесі
нүктесі
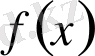 функциясының ерекше нүктесі болады.
функциясының ерекше нүктесі болады.
Анықтама.
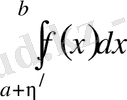 интегралының
интегралының
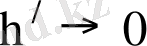 - дағы шегі
- дағы шегі
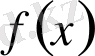 функция-сының
функция-сының
 -дан
-дан
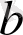 - ға дейін алынған меншіксіз интегралы деп аталады және ол мына теңдікпен анықталады
- ға дейін алынған меншіксіз интегралы деп аталады және ол мына теңдікпен анықталады
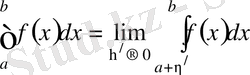 (2)
(2)
Жалпы жағдайда
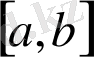 аралығында саны ақырлы
аралығында саны ақырлы
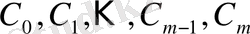 ерекше нүктелер болуы мүмкін. Бұл нүктелерге жақындағанда
ерекше нүктелер болуы мүмкін. Бұл нүктелерге жақындағанда
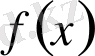 функциясы шенелмеген. Бірақ ерекше нүкте жоқ аралықтарда
функциясы шенелмеген. Бірақ ерекше нүкте жоқ аралықтарда
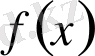 функциясы шенелген және интегралданады.
функциясы шенелген және интегралданады.
Айталық, анығырақ және қарапайым болу үшін, бұндай нүктелер үшеу болсын. Олардың екеуі
 мен
мен
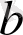 шекараларымен дәл келсін де, ал үшщіншісі с олардың арасында болсын.
шекараларымен дәл келсін де, ал үшщіншісі с олардың арасында болсын.
Онда
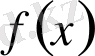 функциясының
функциясының
 - дан
- дан
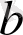 - ға дейін алынған меншіксіз интегралы мына теңдікпен анықталады
- ға дейін алынған меншіксіз интегралы мына теңдікпен анықталады
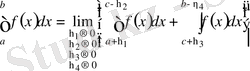 . (3)
. (3)
 аралықтарының әрқайсысынан сәйкес
аралықтарының әрқайсысынан сәйкес
 нүктеден алып, мынаған келеміз:
нүктеден алып, мынаған келеміз:
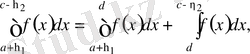
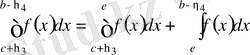 .
.
Оңай көруге болады, (3) шектің бар болуы жоғарыдағы төрт интегралдың күн бұрын бар болуымен тең күшті. Олай болса (3) - тің анықталуын мынамен алмастыруға болады:
 бірақ оң жағындағы барлық меншіксіз интегралдар бар деп ұйғару керек.
бірақ оң жағындағы барлық меншіксіз интегралдар бар деп ұйғару керек.
(2) және (3) меншіксіз интегралдар үшін де (1) меншіксіз интеграл үшін терминдер сақталады.
Мысалдар.
2)
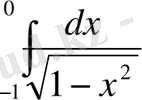 берілген. Интеграл астындағы функция үшін
берілген. Интеграл астындағы функция үшін
 ерекше нүкте.
ерекше нүкте.

3)
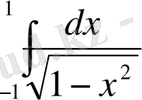 берілген. Интеграл астындағы функцияның
берілген. Интеграл астындағы функцияның
 және
және
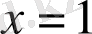 екі ерекше нүктесі бар
екі ерекше нүктесі бар
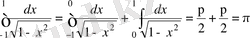 .
.
4)
 - нің қандай мәндерінде мына меншіксіз интеграл жинақ-талатынын зерттелік:
- нің қандай мәндерінде мына меншіксіз интеграл жинақ-талатынын зерттелік:
 . (4)
. (4)
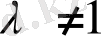 болғанда интеграл
болғанда интеграл
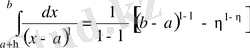
 - нің мәніне байланысты әртүрлі жағдайда болады.
- нің мәніне байланысты әртүрлі жағдайда болады.
Шынында,

Егер де
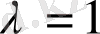 болса, онда
болса, онда
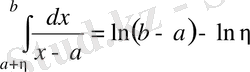 болады. Бұдан
болады. Бұдан
 .
.
Сөйтіп, (4) интеграл
 болғанда
болғанда
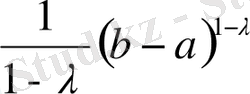 мәніне ие, яғни жинақталады, ал
мәніне ие, яғни жинақталады, ал
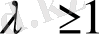 болғанда жинақталмайды.
болғанда жинақталмайды.
5)
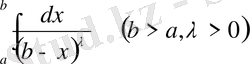 интегралы да осылай зерттеледі.
интегралы да осылай зерттеледі.
2. 2 Интегралдық есептеудің негізгі формуласын қолдану
Айталық
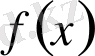 функциясы
функциясы
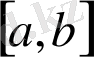 аралығында анықталған және әрбір
аралығында анықталған және әрбір
 аралығында интегралданатын болсын. Бұл жағдайда
аралығында интегралданатын болсын. Бұл жағдайда
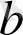 нүктесі
нүктесі
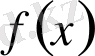 функциясы үшін ерекше нүкте болып табылады. Егер
функциясы үшін ерекше нүкте болып табылады. Егер
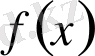 функциясы үшін
функциясы үшін
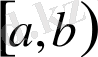 аралығында, яғни
аралығында, яғни
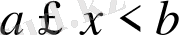 үшін алғашқы функция
үшін алғашқы функция
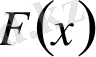 бар болса, онда
бар болса, онда
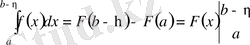 ,
,
және (1) меншіксіз интегралдың бар болуы мына
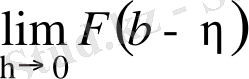 ақырлы шектің бар болуына тең күшті. Егер соңғы шек бар болса, онда оны
ақырлы шектің бар болуына тең күшті. Егер соңғы шек бар болса, онда оны
 - нің мәні үшін қабылдау табиғи, яғни
- нің мәні үшін қабылдау табиғи, яғни
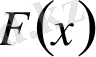 алғашқы функциясының
алғашқы функциясының
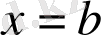 болғандағы мәні. Тек
болғандағы мәні. Тек
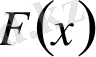 функциясының бүкіл
функциясының бүкіл
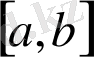 аралығы бойынша үзіліссіздігіне қол жеткізіп алсақ. (1) интегралды есептеу үшін онда біз әдеттегі түрдегі мына формулаға келеміз:
аралығы бойынша үзіліссіздігіне қол жеткізіп алсақ. (1) интегралды есептеу үшін онда біз әдеттегі түрдегі мына формулаға келеміз:
 . (5)
. (5)
Бұл формула өз орнында қалады және сондай жағдайда да, егер ерекше нүкте аралықтың ішінде жатса да немесе бірнеше ерекшелер болады. Тек
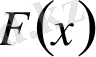 алғашқы функциясының туындысы барлық жерде
алғашқы функциясының туындысы барлық жерде
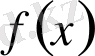 -ке тең болса (ерекше нүктелерді шығарып тастағанда) . Бұл деген сөз
-ке тең болса (ерекше нүктелерді шығарып тастағанда) . Бұл деген сөз
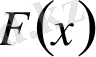 функциясы ерекше нүктелерде де үзіліссіз болатын болсын. Бұндай алғашқы функцияның бар болуы меншіксіз интегралдың бар болуын қамтамасыз етеді.
функциясы ерекше нүктелерде де үзіліссіз болатын болсын. Бұндай алғашқы функцияның бар болуы меншіксіз интегралдың бар болуын қамтамасыз етеді.
(5) негізгі формулада
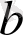 - ні
- ні
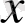 - пен, ал
- пен, ал
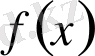 - ті
- ті
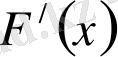 - пен алмастырып, біз оны мына түрде жазуымызға болады:
- пен алмастырып, біз оны мына түрде жазуымызға болады:
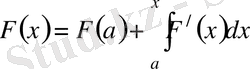 .
.
Сөйтіп, берілген
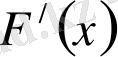 туынды бойынша
туынды бойынша
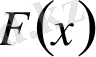 алғашқы функциясы тіктеледі, егер тек туынды интегралданатын болса.
алғашқы функциясы тіктеледі, егер тек туынды интегралданатын болса.
Мысалдар.
1)
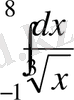 берілген. Бұл жерде интеграл астындағы функ-ция
берілген. Бұл жерде интеграл астындағы функ-ция
 үшін
үшін
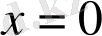 ерекше нүкте. Оның алғашқы функциясы
ерекше нүкте. Оның алғашқы функциясы
 . Ол алғашқы функция
. Ол алғашқы функция
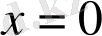 нүктесінде үзіліссіз. Онда интеграл бар болады:
нүктесінде үзіліссіз. Онда интеграл бар болады:
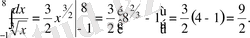
2)
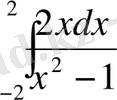 интегралы жоқ, себебі
интегралы жоқ, себебі
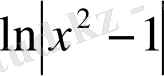 алғашқы функциясы
алғашқы функциясы
 ерекше нүктелерінде
ерекше нүктелерінде
 - ке айналады.
- ке айналады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz