Сызықтардың түйіндесуі

1 Сызықтардың түйіндесуі 3
1.1 Шеңбер доғасымен түзу сызықтардың түйіндесуі 3
1.2 Шеңбер доғаларының түйіндесуі 8
1.3 Қисықтар түйіндесуі, жанасу құрылымы 13
1.3.1 Эллипс 13
1.3.2 Парабола 14
1.3.3 Гипербола 16
1.3.4 Циклойда 19
1.3.5 Эпициклоид 22
1.3.6 Кардиоида 22
1.3.7 Синусоид 23
1.3.8 Архимед қиыршығы 23
1.3.9 Гипоциклоид 25
1.3.10 Астроида 25
1.3.11 Эвольвента 26
Әдебиеттер 28

Сызықтардың түйіндесуі – бір сызығынан басқа сызығына үшінші сызығының көмегімен біртіндеп өтуді айтады.
Қосалқы «біртіндеп өтуді» тура сызықтар түйіндесуінде қисық сызықпен ерекше көрініске ие болады, түзу қисыққа айналыс нүктесінде жанасады. Қисық сызықтар түйіндесуінде көшу нүктесі арқылы олардың жалпы қатыстылығы араласады.
1.1 Шеңбер доғасымен түзу сызықтардың түйіндесуі
L және m түзулері берілген (1 сурет), міндетті түрде олардың баяу қарқынды түйіндесуі R радиусы бар шеңбер доғасында іске асыру керек. Түйіндесуді құру үшін міндетті түрде доға центрін О-нүктесін және А, В түйіндесу нүктелерін табу қажет.
О нүктесі доға центрі – (1а,б,в сурет ) L және m түзулеріне параллель және олардан R қашықтықта орналасқан түзулер қиылысында орын алған.
А және В түйіндесу нүктелері – О нүктесінен L және m түзулеріне түсірілген перпендикуляр негізі болады.
1-ші суретте түйіндесу доғасының радиусы берілмеген, бірақ орын алған С түзуі доға орталығы – О нүктесінде жайғасқан. Доға центрін анықтау үшін L және m түзулері бұрыштарының биссектрисасын құру жеткілікті, к - түзуін. С және К түзулерінің қиылысында О нүктесін табамыз. О нүктесінен L және m түзулеріне перпендикулярлар түсіріп, А және В түйіндесу нүктелерінің және R радиусының шамасын табамыз.

1 Боголюбов С. К., Воинов А. В. Черчение : учебник для машиностроительных специальностей средних специальных учебных заведений. – 2-е изд., перераб. и доп. – М. : Машиностроение, 1984. –304 с.
2 Власов М. П. Инженерная графика. – М. : Машиностроение, 1979. – 285 с.
3 Годик Е. И., Хаскин А. М. Справочное руководство по черчению. - 4-е изд., перераб. и доп. – М. : Машиностроение, 1974. –696 с.
4 Куликов А. С. Проекционное черчение. – М. : Машиностроение, 1968. – 385 с.
5 Левицкий В. С. Машиностроительное черчение. – М., 2000. – 298 с.
6 Миронова Р. С., Миронов Б. Г. сборник заданий по черчению: учеб. пособие для немашиностр. спец. техникумов. – М. : Высш. школа, 1984. – 264 с.
7 Могильный М. М. Техническое черчение. – М. : Машгив., 1971. – 456 с.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

h1
Сызықтардың түйіндесуі
Жоспар

1 Сызықтардың түйіндесуі 3
1.1 Шеңбер доғасымен түзу сызықтардың түйіндесуі 3
1.2 Шеңбер доғаларының түйіндесуі 8
1.3 Қисықтар түйіндесуі, жанасу құрылымы 13
1.3.1 Эллипс 13
1.3.2 Парабола 14
1.3.3 Гипербола 16
1.3.4 Циклойда 19
1.3.5 Эпициклоид 22
1.3.6 Кардиоида 22
1.3.7 Синусоид 23
1.3.8 Архимед қиыршығы 23
1.3.9 Гипоциклоид 25
1.3.10 Астроида 25
1.3.11 Эвольвента 26
Әдебиеттер 28
h3
h41 Сызықтардың түйіндесуі

Сызықтардың түйіндесуі – бір сызығынан басқа сызығына үшінші сызығының
көмегімен біртіндеп өтуді айтады.
Қосалқы біртіндеп өтуді тура сызықтар түйіндесуінде қисық сызықпен
ерекше көрініске ие болады, түзу қисыққа айналыс нүктесінде жанасады. Қисық
сызықтар түйіндесуінде көшу нүктесі арқылы олардың жалпы қатыстылығы
араласады.h4

h41.1 Шеңбер доғасымен түзу сызықтардың түйіндесуі

L және m түзулері берілген (1 сурет), міндетті түрде олардың баяу
қарқынды түйіндесуі R радиусы бар шеңбер доғасында іске асыру керек.
Түйіндесуді құру үшін міндетті түрде доға центрін О-нүктесін және А, В
түйіндесу нүктелерін табу қажет.
О нүктесі доға центрі – (1а,б,в сурет ) L және m түзулеріне
параллель және олардан R қашықтықта орналасқан түзулер қиылысында орын
алған.
А және В түйіндесу нүктелері – О нүктесінен L және m түзулеріне
түсірілген перпендикуляр негізі болады.
1-ші суретте түйіндесу доғасының радиусы берілмеген, бірақ орын алған
С түзуі доға орталығы – О нүктесінде жайғасқан. Доға центрін анықтау үшін L
және m түзулері бұрыштарының биссектрисасын құру жеткілікті, к - түзуін. С
және К түзулерінің қиылысында О нүктесін табамыз. О нүктесінен L және m
түзулеріне перпендикулярлар түсіріп, А және В түйіндесу нүктелерінің және R
радиусының шамасын табамыз.h4

а) R
б)

А В
A B
О

R
R R R

l m
l m

в) г)

R

с

O А В

R
R
к m

О нүктесі – доға центрі, А және В – түйіндесуі нүктелері

1 сурет – L және m түзулердің және R радиус шеңберлер доғаларымен
түйіндесуі

Анағұрлым күрделі есептер деп – түзулердің шеңбер доғаларымен
түйіндесу есептерін санайды (2 сурет). (2а, б сурет) есептерде доға радиусы
R белгілі. Центрді және R радиусын табу суреттер ыңғайынан көрініс табады.
(2 в, г, д сурет) есептерде R1 радиусының доғасы, L түзуі және А
түйіндесу нүктесі берілген. Екінші В түйіндесу нүктесін және R радиусының
табу қажет.
(2 в сурет) есепті шешу. А нүктесінен түрғызылған n1
перпендикулярында, С және О1 нүктелерін қосып С нүктесін табамыз және О1 С
кесіндісіне орталық перпендикуляр тұрғызамыз. n1 және n2 перпендикулярлар
қиылысында О нүктесін және R радиусын, ал ОО1 кесіндісін ұзарта отырып В
нүктесін табамыз.
(2 г сурет) есебінің шешімі (2в сурет) есебіне ұқсатып ыңғайда
шешіледі. Шешімнің басқа нұсқасы 2д суретінде орын алған. Мұнда О1 С
кесіндісін құрастырып, АВ түзуінен О1С түзуіне параллель жүргізе отырып В
нүктесін табамыз.
(2 е сурет) есебінің шешімі (2 в сурет) есебіне ұқсатып шығарылады. А
нүктесін табу үшін АВ түзуінің бағытын білген жеткілікті. (n1) туынды
перпендикулярда l түзуіне С нүктесін аламыз, сол арқылы m1m түзуін О1В
түзуіне паралелль жүргіземіз. m және (n1) түзулер аралығындағы бұрыш
биссектрисасы - (n2) түзуі, ал (n2) түзуіне перпендикуляр - АВ түзуіне
паралель – (n3) түзуі.
АВ түзуі n3 түзуіне паралелль шартты қолданып, L түзуінде А нүктесін
табамыз. Әрі қарай, (n2) орталық перпендикулярды АВ кесіндісіне тұрғызып,
оның n1 перпендикулярынан қиылысқан нүктесінде О нүктесін табамыз.
(2е сурет) О нүктесін басқа жолмен де табуға болады. Ол үшін В
нүктесі арқылы t жанамасын жүргізіп, t және l түзулері арасындағы бұрыштың
b бисектрисасын саламыз, О1В және b түзулер қиылысында О, А нүктелерін және
R радиусын табамыз. Осы жолмен есептің шешуінің фрагменті оң жақтағы (2е
суретте) орын алған.
Түйіндесудің (2 сурет) қарастырылған түрлері әрдайым мүмкін бола
бермейді. Оларды мүмкін емес, егер А нүктесі шеңберде жатса немесе R
радиусы (2а сурет) лайықты өлшемнен кем болғанда. Бұл өлшемдерді мына
теңсіздіктерде арқылы анықтауға болады: О1А ≥ О1О + ОА; О1 ≥ R1 + R + R;
О1А ≥ R1 + 2R; R ≤ 0,5(О1А - R1)

а) б) R1-R

O1
O
O1
R B R
R1
O R B
R
R l
A A

в) г)
n2 O

О1
O1 n1
В n
B D C R 1
О
l

А
A l R R1

C
д)
е)
R1

O1

B n1
R1 O O1
l B n2 C
A O n3 m
R R1

C R A

а, б – R радиусы белгілі; в, г, д – А түйіндесу нүктесі берілген; е –
В түйіндесу нүктесі берілген

2 сурет – R1 радиус шеңберінің доғасының түйіндесу l түзуімен радиус
R шеңберінің доғасымен
Есеп
R радиусы щеңберінің доғасының АВ түзумен түйіндесуін табамыз (3
сурет).
Есеп келесі ретімен орындалады:
1) О1 нүктесін - түйіндесу центрін табамыз, АВ түзуі параллель қиылысу
нүктесі ретінде, одан r қашықтықта орналасқан және R + r радиусы
шеңберлердің доғалары;
2) О1 нүктесінен АВ түзуіне перпендикуляр түсіреміз. Перпендикулярдың
негізі – D нүктесі – түйіндесу нүктесі.
3) түзумен щеңбердің О центрін және О1 түйіндесу ортасын қосамыз,
шеңбердің айналымын қия отырып, екінші Е түйіндесу нүктесінің орны
анықталады.

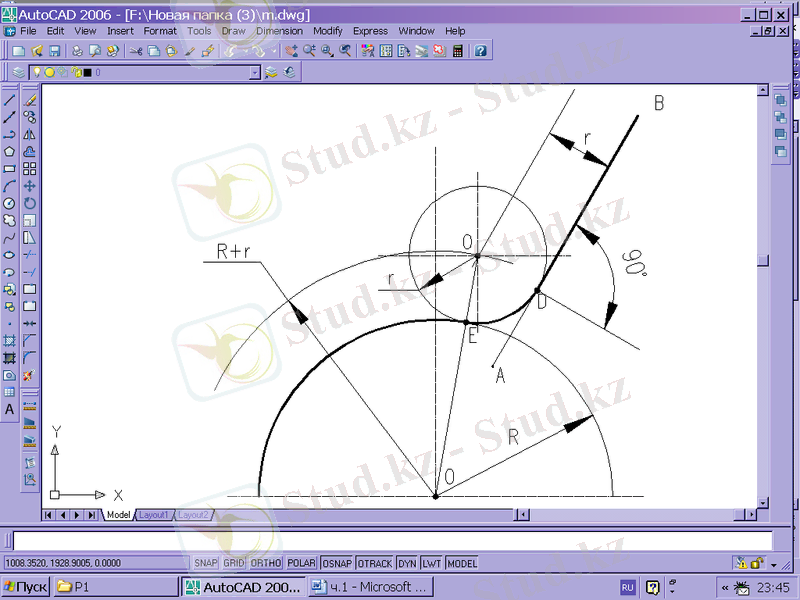
3 сурет – АВ түзу сызығының сыртқы түйіндесу реті (доғамен)

Есеп
R радиусымен берілген шеңбер доғасының түзумен түйіндесуі, түзу АВ
кесіндісімен берілген. r - доға радиусымен.
Есептің шешімі келесі ретімен жүзеге асырылады:
1) О нүктесін - түйіндесу центрін табамыз, АВ түзуі параллель қиылысы
нүктесі ретінде, одан r қашықтықта орналасқан және R + r радиусы
шеңберлердің доғалары;
2) О1 нүктесінен АВ түзуіне перпендикуляр түсіреміз. Перпендикулярдың
негізі – D - түйіндесу нүктесі.
3) Шеңбердің О центрін түйіндесу О1 центрмен түзу арқылы қосамыз,
аталмыш шеңберді қия отырып, екінші Е түйіндесу нүктесінің орны
анықталынады.

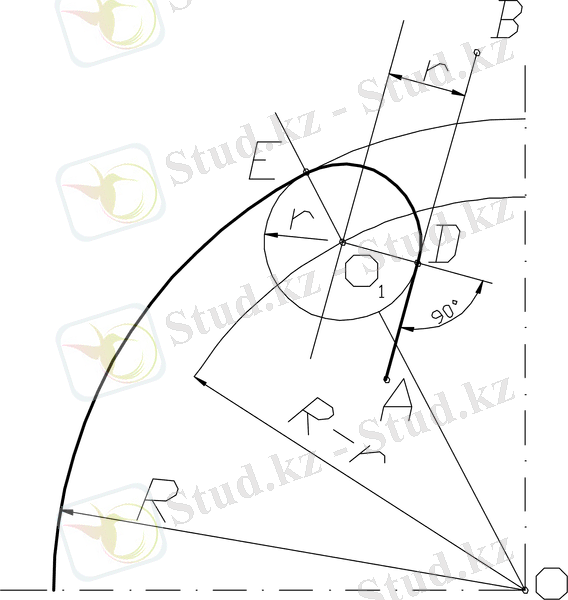
4 сурет – АВ түзу сызығының r радиусы доғасымен ішкі түйіндесу

1.2 Шеңбер доғаларының түйіндесуі

Шеңбер доғаларының түйіндесуінің жай жағдайлары 5-ші суретте орын
алған. R радиусы түйіндесу доғаларының ортасын және О нүктесін табу реті
5 а-д суреттерінен белгілі. А және В көшу нүктелері түзулерде орналасқан,
R1 және R2 радиуысты доғаларының ортасын біріктіреді және О1, О2 нүктелері
R радиус түйіндесуі доғасы ортасымен, О нүктесімен ұштасады.

а) б)
R R2 –K
B A B
A
O
O R1-R
O1 R

o2
R1
O1
R2
O2

в) г)

R1
R-R1

R1

R2
A
R-R2
O1

O2 O1
R
O2
B
A

B

R2
д)
е)

R1

A
R1
R R2

O2
B

O1
O2
A
R2

а - д – R радиусты доға; е – міндетті түрде

(5е сурет) R1 және R2 радиус доғалары бір жалпы А нүктесіне ие, бұл
да өту нүктесі болып табылады.

5 сурет – R1 және R2 радиусты шеңбер доғаларының түйіндесуі
Шеңбер доғасы түйіндесуінің анағұрлым күрделі жағдайлары овалдарда
және овоидтерде (6 сурет) кездеседі.
Әр осындай овал төрттігінде (6а сурет) R1 және R2 радиуысының екі
доғасы, О1 және О2 нүктесі (6а сурет) белгілі және бір жартылай ось шамасы
айқын, a2 және β2 бұрыштарына сүйелді.
Шеңбер доғалары түйіндесу құрылымында овал төрттігі келесі жағдайларда
кездесуі мүмкін: доғалардың центрлері, О1 және О2 нүктелері (6а сурет)
белгілі және бір жартылай ось өлшемі айқын, мысалы ОС. Атап өтерлігі, a2
және β2 бұрыштары белгілі, R1 радиусы = О1С. R1 радиус доғасын құра
отырып, оның және О1, О2 түзулерінің қиылысында А өту нүктесін барысын
айқындап және R2 (R2 = О2А) радиусы өлшемін анықтаймыз. R2 радиусымен овал
төрттігінің екінші доғасын құраймыз:
а) ОС овалының жартылай өсі белгілі және О1 центрінің орналасуы айқын
(6б сурет), осы орайда О1О = О1,С = R1. ОС радиусымен доғаны құра отырып,
О2 центрін табамыз және әрі қарай R1 және R2 = О2А радиуыстарымен овалдың
төрттен бірін құраймыз;
б) ОС және ОД (6в сурет) овалдарының жартылай осі белгілі. ОС
радиусымен доғаны құра отырып, Е нүктесін табамыз. DЕ радиус доғасы
көмегімен F нүктесін құрамыз, n орталық перпендикулярды СF кесіндісіне
тұрғызып О1, және О2 нүктелерін табамыз. R1 = О1С және R2 = О2D
радиустарымен овал доғасын құрамыз;
в) ОС және ОD (6д сурет) жартылай өстері белгілі, ОСЕD тік бұрышын
және DСЕ, СDЕ екі бұрыштын биссектрисасы құрамыз. Биссектрисалар
қиылысында доғалар нүктесінің өту барысын, овалдың төрттен бірін – А
нүктесін қадағалаймыз. А нүктесінен СD түзуіне перпендикуляр түсіреміз
және О1, О2 центрін табамыз, қалыпты түрде радиустар ыңғайы былайша
сипатталады: R1 = О1С= О1А, R2 = О2А= О2D.

R1 С R1 С

А А

О1 О1 R2

В2
О2
R2 О2 О

С R1 C
E
n
R1 A

О1 n O1

O2 O
О2 R2 E R2 D
D

C

A

R1
R2
O1
O2
O D

а) О1 О2 нүктелерінің орналасуы белгілі, ОС жартылай осі шамасы;
б) О1 нүктесінің жартылай осі ОС ауқымы белгілі,егер О1О= О1С = R1;
в, г) ОС және ОD жартылай остері белгілі;
д) ОС жартылай осі және О1 нүктесінің орналасуы белгілі, О1О = О,5 R1

6 сурет – Овалдың шеңбер доғасының төрттен бірінің түйіндесу құрылымы

Есеп

R1 және R2 (7 сурет) радиустарының доғасының сыртқы түйіндесуін табу.

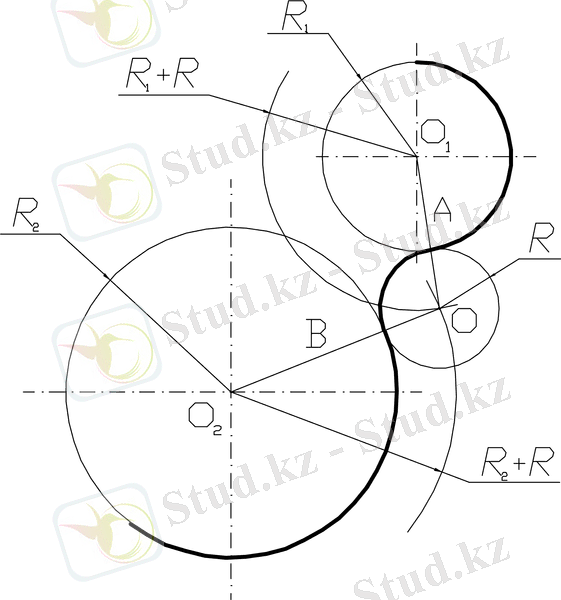
7 сурет – R1 және R2 радиустары доғасының түйіндесуі

Сыртқы түйіндесуде О1 және О2 орталары түйіндесу доғаларының R1 және
R2 радиустары R радиусы доғаларының түйіндесуде ыңғай алады.
Доғалар түйіндесуінің сыртқы көрінісі келесі ретінде іске асырылады:
1) түйіндесу центрін табамыз, шеңбер доғаларының R1 + R радиустарымен
қиылысу О нүктесін және R2+ R радиустарымен шеңбердің шоғырланымы R1
және R2 радиустарымен сәйкес деп есептеледі;
2) О түйіндесу центрін О1 және О2 шеңберлер центрлерімен түзу
арқылы қосамыз, осы орайда берілген шеңбермен қиылыса отырып, А және В
түйіндесу нүктелерінің орындары анықталады;
3) түйіндесуді құрды.

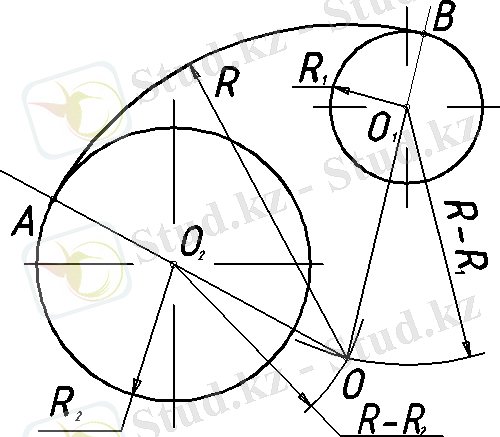
Есеп
R1 және R2 (8 сурет) радиустары доғасының ішкі түйіндесуін анықтау.
Ішкі түйіндесуде О1 және О2 центрінің түйіндесу доғаларының R1 және
R2 радиустарында R радиусы түйіндесу доғаларының ішінен орын алады.
Доғалардың ішкі түйіндесуі келесі ретпен іске асады:
1) түйіндесу центрін табамыз, шеңбердің доғаларының R1 + R
радиустарымен қиылысу О нүктесін және R2+ R радиустарымен шеңбердің
шоғырланымы R1 және R2 радиустарымен сәйкес деп есептеледі;
2) О түйіндесу центрін О1 және О2 шеңберлер центрлерін түзу
арқылы қосамыз, осы орайда берілген шеңбермен қиылыса отырып, А және В
түйіндесу нүктелерінің орындарын анықталады;
3) түйіндесу құрылады.

8 сурет – R1 және R2 радиустары доғаларының ішкі түйіндесуі

Есеп
Доғалардың аралас түйіндесуін табу.
Аралас түйіндесуде осы үрдіске енетін О2 центрі доғаларда R радиусы
доғасының түйіндесу түрі ішінен орын алады, ал О1 центрі басқа түйіндесу
доғасында одан тыс орын алады.
Доғалардың ішкі түйіндесуі келесі ретінде атқарылады:
1) түйіндесу центрін табамыз, шеңбер доғаларының R1 + R радиустарымен
қиылысу О нүктесін және R2+ R радиустарымен шеңбердің шоғырланымы R1
және R2 радиустарымен сәйкес деп есептеледі;
2) О түйіндесу центрін О1 және О2 шеңберлер центірлерін түзу
арқылы қосамыз, осы орайда берілген шеңбермен қиылыса отырып, А және В
түйіндесу нүктелерінің орындары анықталады;
3) түйіндесу құрылады.

9 сурет – Доғалардың аралас түйіндесуі

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.