Мектеп математикасының тарихи мағлұматтары

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 55 бет
Таңдаулыға:

Жоспар:

Кіріспе:

II. Негігі бөлім:

1. V-XI сыныптар математикасының тарихи мағлұматтары

а) V-IX сыныптар математикасының тарихи мағлұматтары

ә) X-XI сыныптар алгебрасы және анализ бастамаларының тарихи мағлұматтары

б) VII-XI сыныптар геометриясының тарихи мағлұматтары

2. Математиктердің өмірлері мен шығармашылықтары

а) Грек және Орта Азия математиктері

б) Еуропа және Орыс математиктері

III. Қорытынды

Әрбір ғылымның дамуына байланысты өздеріне тән ерекше тарихы болады. Сол ғылымдардың тарихын білмей, оның теориясын, практикадағы маңызын және өмірімен байланыстығын жете түсіну қиын болар еді. Сондықтан орта мектепте оқытылатын математиканың тарихи мағлұматтарына ерекшк көңіл бөлген жөн.

Бұндағы мақсатымыз орта мектеп математикасындағы тақырыптарды өзінің тарихымен байланыстыра оқыту.

Математика даму тарихында ұлы математиктердің еңбектері арқылы қалыптасып, ғылымға өшпес із қалдырған. Олардың өмірі жастар үшін зор тәрбиелік маңызы бар. Сондықтан дарынды математиктердің өмірлері мен шығармашылықтарына көңіл бөлген дұрыс. Математиктердің есімдері және математиканың тарихи мағлұматтары бір - бірімен байланыстыра баяндалады.

Зерттеу тақырыбы: Мектеп математикасының тарихи мағлұматтары.

Зерттеу нысыаны: Орта мектеп оқушылары мен мұғалімдері.

Зерттеудің мақсаты: Орта мектеп математикасындағы тақырыптарды өзінің тарихымен байланыстыра оқыту.

1. V-XI сыныптар математикасының тарихи мағлұматтары

1. 1. V-VI сыныптар математикасының тарихи мағлұматтары

Арифметикалық симвалдар мен амалдар

XVI ғасырдың ақырына дейін арифметикада қазіргідей амал таңбалар, теңдік, теңсіздік белгілері және жақшалар қолданылмады.

Қосу (+) мен азайту (-) таңбалары . Бұл таңбалар XV ғасырдың аяқ кезінде Италия ғалымы Леонардо да Винчи мен неміс математигі И. Видманның (1489ж) еңбектерінде алғаш рет кездеседі. Қосу таңбасы латынның «et» (және) деген жалғауының қысқартылып жазылуынан шықты деп есептелінеді. Олай деудің себебі XII ғасырдың қолжазбаларында «et» жалғау латынның «t» әрпі тәрізді болып жазылған.

Қосу мен азайту таңбаларының “плюс” және “минус” деген атаулары латынның “plus”- артық, “minus”- кем деген сөздерден шыққан. Қосу мен азайту таңбаларының орнына көпке дейін осы сөздердің алғашқы әріптері (p мен m) қолданылған кез де болды.

Көбейту (х, ∙) мен бөлу (:, -) таңбалары. Айқыш сызықты (х), мүмкін қосу таңбасына ұйқастырған болар, көбейту таңбасы ретінде алғаш рет ағылшын ғалымы Вильям Оутред (1571-1600) қолданды. Оутред математикада әріптер қолдану жөнінде де едәуір еңбек етті. Көбейту таңбасы ретінде нүктені әуелі Регномонтан, содан кейін, оның маңызын көрсете отырып, Лейбниц қолданды. XVII ғасырларда көбейтудің әр түрлі бірнеше таңбасы болды.

Теңдік(=), теңсіздік(›, ‹) беглілері мен жақшалар. Ағылшындық математик және дәрігер Роберт Рекорд (1510-1558) өзінің “Тапқырлыққа тарту” (1557ж. ) атты еңбегінде «Ұзындығы бірдей екі сызықшадай болып еш нәрсе тең бола алмайды» деп алғаш теңдік белгісін қолданды.

1631 жылы алғаш рет ағылшын математигі Т. Хәриот қолданған теңсіздік белгілері басқа математикалық таңбалардай емес, математикаға бірдей кіріп, сіңісіп кетті, өйткені математикалық жаңа таңбаларды қолдануға көбіне типографиялық таңбалардың жоқтығы және оларды жасатудың қиындығы бөгет болып келген болса, бұл таңбалардың орнына латынның V әрпі пайдаланылып, ондай қиыншылық кездеспейді.

Араптар арифметиканы үнділерден үйренді, сондықтан да әл-Хореми еңбегін “Үнді арифметикасы” деп атады. Үнділер ол кезде арифметикалық амалдарды қазіргі бізше қосумен азайтудан бастамай, мысырлықтарша (мүмкін солардан үйренген болар), екі есе арттыру мен екі есе еселеуден басталуы ғажап емес.

Әр елде әр кезде қолданылған арифметикалық амалдарды өту тәртібі әр түрлі болды. Орта ғасырлардағы арифметикалық оқулықтарында мынадай 9 амал қолданылды:

нумерация;
қосу;
азайту;
екі еселеу;
көбейту;
екіге бөлу;
бөлу;
прогрессия (натурал сандар қатарының қосындысын табу) ;
түбір табу (квадрат түбір) ;

Қосу амалы. Қазіргі сияқты, бірақ сол жақтан бастап қосу тәсілі Үндістаннан шықты. Мұндай сол жақтан (жоғарғы разрядтан) бастап қосу ауызша есептеулерде қазір де қолданылады.

XIII ғасырлардың орта кезінде Францияда санды оң жағынан (төменгі разрядтан) бастап қосу тәсілі шықты, ол XV ғасырларда қазіргідей болып қалыптасты.

Азайту амалы. Азайту амалы әр кезде әр түрлі мынадай екі тәсілмен орындалып келеді:

азайғыштың азайтқыштан артығын табу;
азайтқышқа қосқанда азайғышпен теңелетін санды табу.

Бірінші тәсіл Үндістаннан шыққан.

Шотландия математигі Непердің 1617 жылы ойлап шығарған таяқшалары арқылы кез келген санды біріне-бірін көбейту жоғарыда айтылған “тор көз тәсілі” бойынша орындалады, мысалы: 456-ны 76-ға көбейту үшін Непер таяқшаларының ішінен нөлдік, төрттік, бестік, алтылық таяқшаларды алып, оларды таблицада көрсетілгендей етіп орналастырамыз да 456-ны 7-ге, 10-ға, яғни 70-ке, содан кейін 6-ға көбейтіп, екі көбейтіндіні қосамыз:

456∙76=456∙(70+6) =456∙7∙10+456∙6=31920+2736=34656

Бөлу амалы. Амалдардың ішіндегі адамға ең қиын тигені − бөлу. Бөлуді білген кісі едәуір мәдениетті адам саналып, оған “абак докторы” деген атақ берілетін.

Сөйтіп, көп таңбалы санды біріне-бірін бөлу амалының орындалу техникасы көпке дейін ретке қойылмай, тек XV-XVI ғасырлардан бастап (ондық бөлшек шыққаннан кейін) қазіргідей (қалдық ондық бөлшекпен есептелінетін) болып тиянақталады.

Бөлшек санның шығуы. Алғашқы адам әр түрлі нәрселерді өмірде санай жүріп, тіпті ертеде, натурал сандар қатарын тапты. Сонымен қатар ол түрлі нәрсенің ұзындығын (қалыңдығын), ауданын (бетін), көлемін (үлкендігін) өз мүшесінің немесе айналасының көпшілікке жақсы таныс бір нәрсенің ұзындығымен салыстырды.

Бөлшек сандардың даму тарихына көз жіберсек, бөлшектердің мынадай негізгі үш түрін кездестіреміз:

бірлік бөлшектер;
системалы (жүйелі) бөлшектер;
жалпы түрдегі бөлшектер.

Бірлік бөлшектер− бөлшек ұғымы алғаш шыға бастаған кездегі, ең қарапайым ұғым, сондықтан ол тек мысырлықтардан ғана емес, басқа елдерде де, соның ішінде, бөлшектен хабары жоқ қазақ арасында да жарты (½), және (1/4) және тағы басқа ұғымдары болған.

Натурал сандар

Натурал сандар− ең көне математикалық ұғымдардың бірі. Ол мыңдаған жылдар бұрын адамзат қоғамының дамуының алғашқы кезеңінде, адамдардың нәрселерді (мал, балық және т. б. ) санау қажеттігінен туған. Әрине, нәрселерді ол кезде қазіргідей санамаған, алдымен оларды белгілі нәрселермен, дененің бөліктерімен, мысалы, қолдың саусақтарымен санап, көзбен салыстырған, кейіннен санды белгілеу үшін ерекше таңбалар қазіргі цифрлардың алғашқы белгілері пайда болған.

Бізге белгілі 0, 1, 2, . . . , 9 цифрлары үнді елінде пайда болған, және бұдан шамамен 2000 жыл бұрын дүниеге келген. Еуропаға оларды араптар апарған, сондықтан оларды араб цифрлары деп атайды.

Санаудың позициялық принципке негізделген көне жүйесі алты ондық (алпыстық) жүйе болып есептелінеді. Ол ежелгі Вавилонда бұдан шамамен 4000 жыл бұрын шықты. Оны біз қазіргі кезде де пайдаланып жүрміз. Мысалы: 1сағ = 60мин, 1мин = 60сек.

Кей жағдайларда рим цифрлары қолданылады:

I/1, V/5, X/10, L/50, C/100, D/500, M/1000, …

Арифметиканың бізге жеткен ежелгі еңбектерінің бірі армян философы және математигі А. Ширакацидің (XIIғ. ) оқулығы “Сұрақтар мен шешулер”. Ондық нумерациялық алфавит Киев Русінде таралған.

Ежелгі Вавилонда есептеу жұмысын жеңілдету үшін әр түрлі кестелер оның ішінде көбейту кестесін жасады. Ежелгі бірқатар елдерде бірінші есептеу құралы− абак қолданды.

Орта ғасырлық Еуропада Рим цифрларын пайдалану қиын болғандықтан, есептеу жұмыстары абак арқылы орындалды. XII ғасырда әл-Хорезмидің “Арифметикасы” латын тілінде аударылды, осының арқасында еуропалықтар ондық позициялық принциппен танысты. Осы уақыттан бастап, біртіндеп араб цифрларына және жаңа есептеу жүйелеріне өте бастады.

Жай сандар

Ежелгі грек ғалымы Эратосфен (б. э. д. IIIғ. ) жай сандардың кестесін жасауға арналған өзінің тәсілін ұсынды. Бұл тәсіл “Эратосфен елегі” деп аталады. Оның мәні неде? Мысалы, 1-ден 20-ға дейінгі сандардан жай сандарды тізіп жазамыз:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.

Бұдан әрі жай емес сандарды сызамыз. Алдымен, 1-ді үстінен сызамыз, өйткені бұл − жай сан емес. Бірінші жай сан 2, оның астын сызамыз да, барлық 2-ге еселік болатын, 4, 6, . . . , 20 сандарын үстін сызамыз. Келесі жай сан 3, оның да астын сызып, 3-ке еселік барлық санды (сызылмай қалғандарын) сызамыз және т. с. с. Сөйтіп, біз өзімізге қажетті барлық жай сандарды: 2, 3, 5, 7, 11, 13, 17, 19 “електен” өткіземіз.

Сан жөніндегі ұғым − адамзат мәдениетінің тууымен, оның дамуымен тығыз байланысты. Егер осы ұғымды алып тастасақ біздің рухани өміріміз бен практикалық қызметіміз әлсіз болған болар еді. Есеп-қисап жүргізу, уақытты, алыстықты өлшеу, еңбек нәтижелерінің қорытындыларын шығару сан ұғымынсыз мүмкін емес. Адам өмірінде сан ұғымының өте қажеттілігі сонша, өткен замандарда барлық елдердің атақты математиктері натурал сандар ішінде жай сандардың орналасу сырын табумен шұғылданды.

Жай сандарды зерттеу саласында орыс математиктері зор еңбек сіңірді. П. Л. Чебышев (1821-1894) 1-ден үлкен кез келген натурал сан мен берілген саннан екі есе үлкен санның арасында (мысалы, 2 және 4, 3 және 6, 10 және 20, т. б. ) кем дегенде бір жай сан бар болатынын дәледеді. Сандар теориясының негізін қалаушы П. Л. Чебышев болды. И. М. Виноградов(1891-1983) кез келген жеткілікті үлкен санды үш жай санның қосындысы түрінде көрсетуге болатынын ұсынды. Мысалы, 7=2+2+3, 9=3+3+3=2+2+5, 15=3+5+7=5+5+5, т. б.

Жай бөлшектер

Ежелгі заманда-ақ (б. э. б. 2000ж) қарапайым бөлшектер пайдаланылған. Ежелгі вавилондықтар 1/2, 1/3, 2/3, . . . бөлшектерін белгілеуге арналған арнайы белгілері болған. Ежелгі Египетте бірлік бөлшектер, яғни 1/n (мұндағы n-натурал сан) түріндегі бөлшектер пайдаланылған. Егер де өлшеу нәтижесінде 7/8 саны шығатын болса, онда мұны бірлік бөлшектердің қосындысы түрінде жазған: 7/8=1/2+1/4+1/8.

Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Бөлшектер туралы түсініктің дамуына үш түрлі бөлшектер ұғымы қалыптасқан.

Бірлік бөлшектер - аламдары бір болатын үлестер.
Жүйеленген бөлшектер. Оның алымы кез келген бүтін сан, бөлімі тек

10 санының немесе 60 санының дәрежелері ғана болған.

3. Жалпы түрдегі бөлшектер. Оның алымы да, бөлімі де кез келген натурал сан болады.

Бөлшектердің мұндай әр түрлілігі есептеу және өлшеу жұмыстарында көптеген қиындықтар туғызады. Бөлшек ұғымының дамуы ғылым мен сауда- саттық жұмыстары өркендеген елдерде: Египетте, Вавилонда, Үндістанда және Римде қалыптасты.

Жай бөлшектер туралы ілімінің дамуына үнді математиктері көп үлес қосты. Оларда негізгі бөлшекте, яғни 1/3, 1/5, 1/7, т. б. бөлшектердің түрлері кездеседі.

Қазіргі жай бөлшектерді белгілеу VIII ғасырда Үндістанда қабылданған. Бөлшектердің алымы мен бөлімі бөліп тұратын сызықты, грек математиктері Александриялық Герон (б. э. Iғ. ) және Диафант (IIIғ. ), Италия математигі Л. Лизанский (Фибоначчи) (1180-1240) еңбектерінде кездеседі. Бұдан кейін бөлшек сызық барлық жерге жалпылай таралған.

Бірлік бөлшектермен қатар бір мезгілде жүйелі бөлшектер, яғни алымдары кез келген сандар бола алатын, ал бөлімдері белгілі бір санның мысалы, онның, жиырманың, алпыстың дәрежесі болатын бөлшектері шықты. Алпыстық бөлшектер XVII ғасырға дейін пайдаланылып келді. Қазіргі кезге дейін уақыт бірліктері алпыстық жүйемен өрнектеледі.

Грек ғалымы Архимедтің (б. э. д. 287-212) кейбір еңбегінде алымы мен бөлімі кез келген натурал сандар болатын бөлшектің жалпы түрі кездеседі. Ежелгі гректер іс жүзінде жай бөлшектерге барлық амалдарды қолдана білген. Бірақ та бөлшекті қазіргі кездегідей сызықша арқылы жазу болмаған. Сызықша жазу тек 1202 жылы Италия ғалымы А. Фибоначчидің “Абак кітабы” атты шығармасында ғана енгізілген.

Ұзақ уақыт бойы бөлшектерді сандар деп атамаған. Бұларды кейде “сынық сандар” деп атаған. Тек XVIII ғасырда ғана бөлшектерді сандар ретінде қабылдай бастады. Бұған ағылшын ғалымы И. Ньютонның (1643-1727) 1707 жылы жарық көрген “Жалпыға бірдей арифметика” атты кітабы ықпал жасады, мұнда бөлшек ұғымы бір өрнекті екінші өрнекке бөлуден шығатын бөлінді ретінде кеңейтілді.

Ондық бөлшектер

Вавилонда б. э. д. 4000 жыл бұрын ежелгі жүйелі бөлшектерді пайдаланған, ал ежелгі грек астрономдары арқылы Батыс Еуропа астрономдарына алпыстық бөлшек жүйесі тараған.

XVI ғасырдың аяғында тұрмыстық жағдайларға бөлшектердің күрделі есептеулерін пайдалану қажеттілігін басқа ондық бөлшек жүйесі пайдаланылды: 1/10, 1/100, 1/1000, . . . Басқа жүйелерге қарағанда ондық бөлшек жүйесінің артықшылығы, біріншіден жазылуы және оған амалдар қолданылуы бүтін сандарға негізделген.

Оның жазылуы: 7, 305=7+3/10+0/100+5/1000 немесе 7, 305=7 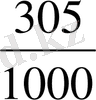. Ондық бөлшектің бүтін бөлігі болмаса, онда үтірдің алдында нөл жазу керек, мысалы, 35/100=0, 35. Ондық бөлшектің қасиеті бойынша былай жазуға болады: 12, 7=12, 70=12, 700 және т. с. с.

Ондық бөлшектерді есептеу натурал сандарды есептеуге ұқсастығына қарай және ыңғайлығына байланысты ғылымдағы, өндірістегі, күнделікті өмірдегі есептеулерде жиі пайдаланылады. Ондық бөлшектер және оларға амалдар қолдану туралы Орта Азия ғалымы әл-Кәши ондық бөлшектерді көбейту мен бөлу тәсілдерін қалыптастырды. Сондықтан ол есептеуде ондық бөлшекті ең алғаш пайдаланған ғалым ретінде тарихқа енген. Әл-Кәши ондық бөлшектерді жазуды үтірді пайдаланбаған, бірақ ол үтірдің орнына тік сызық қойған.

Ондық бөлшекпен есептеу туралы әл-Кәши еңбектерінен кейін 158 жылдан соң голландиялық математик Симон Стевин (1585ж) атты кітабында жазды. Стевин Еуропа елдерінде ондық бөлшектерді есептеу жұмыстарына пайдалануды насихаттады.

Ондық бөлшектің бүтін бөлігін ажыратуды Шотландия математигі Дж. Непер (1550-1617) және аспан әлемін зерттеуші неміс математигі И. Кеплер (1571-1630) енгізген.

Ресейде 1703 жылы Л. Ф. Магницкий (1660-1739) өзінің еңбегі "Арифметика - сандар туралы ғылым" деген оқулығында ондық бөлшектер туралы ұғымды ғылыми түрде баяндаған.

Проценттер

Әр түрлі практикалық есептеулерде проценттерді пайдалану Вавилонда және Ежелгі Римде кеңінен таралған. “Процент” дегеніміз (латынның pro cento - жүзден деген сөз) жүзден бір бөлігі деген мағынаны білдіреді, яғни 1% деген ұғым 0, 01; 27%= 0, 27; 100%=1; 150%=1, 5 және т. б.

Процент белгісі %- cto (cento сөзінің қысқаша жазылуы) сөзінің жазылуының өзгертілген түрі.

Айлық табыстың 1% деп, оның 0, 01-ін айтады, ал жоспар түгел орындалды деген, яғни 100% орындалған, ал жоспар 150% орындалды дегенді 1, 5 жоспар орындалған дегенді білдіреді.

Берілген санның проценттік мәнін табу үшін ол санды 100-ге көбейту керек. Мысалы, 2 санының проценттік мәні 200% болады.

Нақты сандар

Сан ұғымы өте ерте заманда туып, ғасырлар бойы дамыған. Теріс сандар ұзақ уақыт бойы “жалған” сандар деп есептелініп, “қарыз” (“борыш”), “жеткіліксіздік” (“жетімсіздік”) ретінде түсіндіріліп келген. Оң және теріс сандарға амалдар қолданылу ережесі ұзақ уақыт бойы тек қосу және азайту жағдайлары үшін ғана қарастырылып отырған. Мысалы, бұл ережені үнді математиктері VII ғасырда былай тұжырымдаған: “Екі мүліктің қосындысы мүлік болады, екі қарыздың қосындысы қарыз болады, мүлік пен қарыздың қарыздың қосындысы бұлардың айырмасына тең болады”.

XVII ғасырда ғана Декарт пен Ферма енгізген координатор әдісі пайдаланыла бастағаннан бері теріс сандар оң сандармен тең құқықты сандар ретінде қабылданды. Теріс сан практикада теңдеуді шешу кезінде пайда болды.

Бүтін және бөлшек сандар рационал сандар жиынын құрайды. Бұл сандар есептеуге қолайлы екі рационал санның қосындысы, айырмасы, көбейтіндісі және бөліндісі (бөлгіш нөлден өзге сан болғанда) рационал сандар болып табылады. Рационал сандардың тығыздық қасиеті бар, мұның арқасы кез келген дәлдік дәрежесі бойынша өлшеуге және де өлшеу нәтижесін рационал (бүтін және бөлшек) санмен өрнектеуге болады. Сондықтан рационал сандар ұзақ уақыт бойы азаматтың іс жүзіндегі қажеттіктерін толық қамтамасыз етіп келді (және де қазіргі кезге дейін қамтамасыз етуде) . Соған қарамастан шамаларды өлшеу мәселесі жаңа сан, иррационал санның шығуына әкеп тіреді. Ежелгі Грекияда Пифагор (б. э. д. VIғ. ) оқушыларының мектебінде, егер өлшеу бірлігі ретінде квадраттың қабырғасы алынатын болса, онда квадраттың диагоналын рационал санмен өрнектеуге болмайтыны дәлелденбеген болатын.

Квадраттың диагоналы және оның қабырғасы секілді кесінділерді өлшенбейтін кесінділер деп атаған. Бұған кейінгі уақытта (б. э. д. V-VI ғ. ) ежелгі грек математиктері толық квадрат болмайтын кез келген натурал n саны үшін 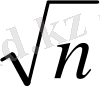санының иррационалдығын дәлелдеді.

Үндістанның, Таяу және Орта Шығыстың, ал кейініректе Еуропаның математиктері иррационал шамаларды пайдаланды. Бірақ ұзақ уақыт бұларды тең құқықты сан ретінде қабылдамай келген. Оларды қабылдауға Декарт (1596-1650) “Геометриясының” шығуы ықпал жасады. Әрбір рационал немесе иррационал сан координаттық түзудің бойындағы барлық “бос орындар” толтырылды. Осы қасиетке сүйеніп, нақты сандар жиыны (рационал сандар жиынынан айырмашылығы) үздіксіз болып табылады делінеді.

Грек математиктері геометриялық алгебраның негізін салды. Кесінділердің ұзындығын иррационал сандармен белгілейді. Орта Азия ғалымдары Омар Хайям (XII ғ. ) және Насыреддин Туси (XII ғ. ) сан ұғымын кеңейтіп, иррационал сандарды рационал сандармен қатар қолданды. Еуропада С. Стевин кез келген нақты санды жазу үшін ондық бөлшектерді қолданды.

Кез келген нақты санды шектеусіз (периодты немесе периодсыз) ондық бөлшектер түрінде көрсетуге болады. XVIII ғасырда Л. Эйлер (1707-1789) кез келген шектеусіз ондық бөлшек иррационал сан болатынын көрсетті. Шектеусіз ондық бөлшектер негізінде нақты сандар құруды неміс математигі К. Вейрштрасс (1815-1897) жасады. Нақты сандар теориясын мазмұндаудың басқаша тәсілдерін неміс математиктері Р. Дедекинд (1831-1961) пен Г. Кантор (1845-1918) ұсынды.

Шамаларды өлшеу

Ерте заманда әр елдің халықтарында ұзындық өлшем әр түрлі болды. Мысалы: шынтақ, табан, ер адамның қадамы және т. б. . Ал, кейбір елдерде келісімді өлшеулер болмағандықтан соған байланысты дау жанжалдар болып тұрған. Ұлы француз халқы республика территориясына өлшеудің бірлік метрлік жүйесін енгізді. Жаңа өлшем бірлік туралы негізі ойлары айтты. Ұзындық бірлігіне 1/1 Париж географиялық меридианның ¼ бөлігі алынды. Бұл меридиананы өлшеу үшін, Дюнкерк және Барселон қалаларының арасында 6 жыл бойы екі француз оқымыстылары Б. Мешен және Даламбер өлшеу жұмыстарын жүргізді.

XVIII ғасырдың аяғында бұл жерде заңды ұзындық бірлігі ретінде метр тағайындалды. Еуропаның басқа елдерінде метрлік жүйені XIX ғасырдың аяғында пайда бола бастады. Ал, Ресейде көне орыс өлшеу бірліктері (мысалы, бір шақырым жуық шамамен 1 км 67 метр, т. б. ) қолданылды. Ресейде метрлік бірлік жүйені енгізу 1889 жылы басталды. Бұл кезеңде ескі өлшеу бірліктері қолданылады. Ресейде алғаш рет ұзындық бірлігі үшін метрді қолданған Н. И. Лобачевский (1792-1856) . Метрикалық жүйені халықаралық дәрежеде ұсынған орыс оқымыстысы Б. С. Якоби (1801-1874) . Ресейде 1809 жылы Менделеев метрлік жүйесін енгізуге келісім алды, сөйтіп бұл өлшеудің жүйесін 1918 жылдан бастап қана міндетті деп саналатын болды. Метрлік жүйеге көшу − бұл маңызды қадам болды. Бір тұтас өлшеу бірлігін пайдалану халықтар арасындағы қарым−қатынасты, мысалы Халықаралық сауда- саттық жүйесіндегі есеп-қисап жасауды едеуір жеңілдетті. Алайда кейбір елдерде дәстүр бойынша қазірдің өзінде де метрлік жүйеге жатпайтын бірліктер қолданылып жүр. Мысалы, Англияда, ұзындық бірліктер ретінде ярд (1ярд≈91см) қолданылады. Оны 1101 жылы I Генрих каролі енгізген болатын.

Есептеу құралдары

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.