Күрделі сызықтардың қисықтықтары мен бұралымдарын есептеу


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
рЕСПУБЛИКАЛЫҚ МЕМЛЕКЕТТІК ҚАЗЫНАЛЫҚ КӘСІПОРЫНЫ
с. аМАНЖОЛОВ АТЫНДАҒЫ ШЫҒЫС ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ТЕХНОЛОГИЯ ФАКУЛЬТЕТІ
Математика кафедрасы
БІТІРУ ЖҰМЫСЫ
Тақырыбы: КҮРДЕЛІ СЫЗЫҚТАРДЫҚ ҚИСЫҚТЫҚТАРЫ МЕН БҰРАЛыМДАРЫ
Өскемен, 2008
МАЗМҰНЫ
КІРІСПЕ 3
1 КҮРДЕЛІ ҚИСЫҚТАР ТЕОРИЯСЫ 6
1. 1 Жазықтықтағы және кеңістіктегі сызықтар. Олардың берілу тәсілдері 6
1. 2 Жазықтықтағы және кеңістіктегі күрделі сызықтар 9
2 КҮРДЕЛІ СЫЗЫҚТАРДЫҢ ҚИСЫҚТЫҚТАРЫН ЕСЕПТЕУ 19
2. 1 Қисықтықты есептеу теориясы 19
2. 2 Күрделі сызықтардың қисықтықтарын есептеу 26
3 КҮРДЕЛІ СЫЗЫҚТАРДЫҢ БҰРАЛЫМДАРЫН ЕСЕПТЕУ 34
3. 1 Бұралымды есептеу теориясы 34
3. 2 Күрделі сызықтардың бұралымдарын есептеу 37
4 ҚИСЫҚТЫҚ ПЕН БҰРАЛЫМДАРДЫҢ АРАСЫНДАҒЫ
БАЙЛАНЫС 45
ҚОРЫТЫНДЫ 47
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 49
КІРІСПЕ
Дифференциалдық геометрия - геометрияның геометриялық бейнелерді (сызықтарды, беттерді және олардың үйірлерін) математикалық анализдің тәсілімен зерттейтін бөлімі. Зерттелетін құбылысты сипаттайтын математикалық заңдылықтар, көбінесе, күрделі болып кедеді де, олар шектеусіз аз облыста қарастырғанда жадағайланып, қарапайым түрде көрінеді. ал қарапайым заңдылықтар мәлім болғанда, бүкіл құбылысқа тән күрделі заңдылықтарды табу мүмкіндігі туады. Дифференциалдық геометрияның түп негізінде осы идея жатыр.
Дифференциалдық геометрия анализдің даму нәтижесінде пайда болып, тығыз байланыста дамыған. Көптеген геометрияның ұғымдары анализдің ұғымдарынан туындаған. Мысалға, жанама ұғымы анализдегі туынды ұғымынан пайда болған. Дифференциалдық геометрия XVIII ғасырда пайда болып, Л. Эйлер мен Г. Монж («Приложение анализа к геометрии», 1795г. ) есімдерімен тығыз байланысты. Келешекте дифференциалдық геометрияның дамуына Гаусс, Н. И. Лобачевский, Б. Риман, Ф. Клейна, Х. Гюйгенс, Бернулли ғалымдарының еңбектерінде көрініс тапты. Дифференциалдық геометрияда алдымен сызықтар мен бетердің шектеусіз аз үйірлерінің қасиеттері айқындалады, содан кейін сызық пен беттің тұтас тұлғасындағы ерекшеліктері айқындалады. 1687 жылы швейцарилық ғалым И. Бернулли (1667 - 1748) берілген бетегі «ең төте жолды» табу туралы есепті жариялады. Бұл есеп дифференциалдық геометрияның алғашқы дәуірінде елеулі рөл атқарды.
Дифференциалдық геометрияда сызықтар теориясының дамуына өз үлесін көптеп қосқан Гюйгенс болатын. Голландияның кемеңгер ғалымы математик, физик және астроном Христиан Гюйгенс ван Цюйлихем 1629 жылы 14 сәуірде Гаага қаласында туған. Жастайынан білімге деген құштарлығы көрінді. Гюйгенс - өз заманының перзенті, Галилей мен Декарттың тікелей мирасқоры. 66 жыл өмірінде ол математика мен физиканың көптеген күрделі мәселелерін шешіп, кейінгі ұрпаққа жол көрсетті. Дифференциалдық геометрияда жеткен жетістіктері көзге көрінерлік. Көптеген күрделі сызықтар, соның ішінде циклойданы, строфойданың, кардиойданың, конхоиданың және т. б. көптеген күрделі қисықтардың теориялық құрылымын қалыптастыруға көп еңбек етті. Олардың теңдеулерін, сызбасының салыну жолдарын терең зерттеген. Гюйгенс қисықтардың эвалютасы мен эволвенталары жөнінде 11 теорема тағайындаған. Эволвенталар мен валюталар теориясы, кейін қисықтықтардың ілімі мен бұралымы жөніндегі ілімінің қалыптасуына себеп болды. Атақты ғалымдардың сөздері бойынша: «Гюйгенс - өз заманының ұлы геометрі» (И. Ньютон) .
1760 жылы Л. Эйлердің қисық сызықтың қисықтығы жөніндегі еңбегі жарыққа шықты. Дифференциалдық геометрияны Петерсон - Майнарди тұрғысынан қарап, оны одан әрі дамытты. Дифференциалдық геометрияда Монж мектебінің (Ф. Френе, О. Бонне, Г. Дарбу, т. б., Франция) , Э. Бельтрами мектебінің (Майнарди, Кодацци, Бианки, т. б., Италия), Гаусс ізбасарларының (Б. Риман, Ф. Клейн, Д. Гильберт, В. Бляшке, т. б., Германия), Петерсон мектебінің (Ф. Миндинг, т. б., Ресей) еңбектері ерекше маңызды орын алды. Сондай-ақ, бұл салада Ресей ғалымдары Н. Н. Лузин (1883 - 1950), Д. Ф. егоров (1869 - 1931), А. Д. Александров (1912), Н. Ф. Ефимов (1910 - 1982), т. б. үздік табыстарға жетті. Қазақстанда дифференциалдық геометрияның геометрия саласында Н. Қ. Білиев жұмыс атқарған болатын.
Бітіру жумысымның зерттеу нысанасы ретінде күрделі сызықтардың қисықтықтары мен бұралымдары алынған.
Бітіру жұмысының негізгі мақсаттары:
- Күрделі сызықтардың теориясын ашып көрсету;
- Қисықтықтар мен бұралымдарды есептеу кезеңдерін нақтылау;
- Осы сызықтардың қисықтықтары мен бұралымдарын есептеп шығару;
Жұмыс барысында күрделі қисықтардың теңдеулерімен, сызбаларының салыну ерекшеліктерімен таныс болып, қисықтықтары мен бұралымдарының есептелу ерекшеліктеріне көп көңіл бөлетін боламыз.
Бітіру жұмысы негізінен төрт бөлімнен тұрады:
1-де жазықтықтағы және кеңістіктегі сызықтар мен олардың берілу тәсілдерімен танысып, жазықтықтағы және кеңістіктегі күрделі сызықтардың негізгі теориялық құрылымын айқындаймыз.
2-де сызықтардың қисықтықтарын есептеу, мұнда жалпы қисықтықтарды есептеп шығару жолдары баяндалады және күрделі сызықтардың қисықтықтары есептеліп шығарылады.
3-де сызықтардың бұралымдарын есептеу жүргізіледі, яғни кеңістіктік сызықтарының бұралымдарын есептеу әдістері қарастырылады және күрделі сызықтардың бұралымдары есептеліп шығарылады.
4-де сызықтардың қисықтықтары мен бұралымдарының арасындағы байланыстар анықталып, көрсетіледі.
Жұмыс барысындағы негізгі міндеттердің бірі күрделі сызықтардың қисықтықтары мен бұралымдарын есептеудің неғұрлым тиімді әдістерімен таныстыру және нақты есептелген мысалдармен негіздеу.
1 КҮРДЕЛІ СЫЗЫҚТАР ТЕОРИЯСЫ
1. 1 Жазықтықтағы және кеңістіктегі сызықтар. Олардың берілу тәсілдері.
Сызықтарды зерттеу үшін олардың нақты анықтамаларын білу қажет. Сызықтардың анықтамаларын шығарып көрейік. С жиыны элементар сызық (жазықтықтықтағы немесе кеңістіктегі) деп аталады егер кесіндінің бейнесі өзара үздіксіз жазықтықта немесе кеңістікте бұл кесіндінің бейнеленуі болып табылса.
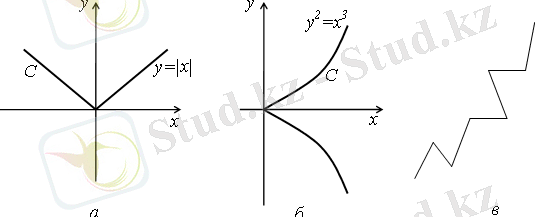
Мысалы элементар сызықтар - бұл шеңбердің, эллипстің доғасы, үздіксіз функциялардың графиктері және т. б. (1- сурет) .
Кесіндінің шеткі нүктесінің бейнесі элементар сызықтың шеткі, ал бастапқы нүктесінің бейнесімен қосатын аралықты доға деп атайды. Элементар сызықтың кезкелген доғасының өзі элементар сызық болатыны анық.
1 - сурет.
Егер элементар С сызық үздіксіз
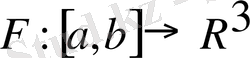 бейнеленетін
бейнеленетін
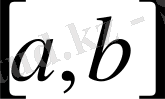 кесіндісінің бейнесі болса, онда кезкелген
Р
нүктесінің сызығында бейнеленуі
кесіндісінің бейнесі болса, онда кезкелген
Р
нүктесінің сызығында бейнеленуі
 тек қана бір санмен анықталады:
тек қана бір санмен анықталады:
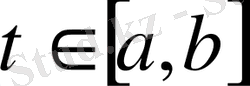 .
t
айнымалысы сызықтың параметрі деп аталады. Параметрдің әртүрлі мәндеріне сәйкес сызықтың әркелкі нүктелері табылады.
F
бейнеленуді
C
түзуінің парметрлизациялануы деп атаймыз. Бір түзудің өзінде әртүрлі параметрлизациялары болуы мүмкін. Параметрлері бар сызықтарды параметрленген сызық деп атайтын боламыз
.
t
айнымалысы сызықтың параметрі деп аталады. Параметрдің әртүрлі мәндеріне сәйкес сызықтың әркелкі нүктелері табылады.
F
бейнеленуді
C
түзуінің парметрлизациялануы деп атаймыз. Бір түзудің өзінде әртүрлі параметрлизациялары болуы мүмкін. Параметрлері бар сызықтарды параметрленген сызық деп атайтын боламыз
(2 - сурет) .
Координаталар жүйесін бекітейік.
 нүктесі
x, y, z
координаталары болсын.
t
параметрінің өзгеруінен олар да өзгеріп отырады, себебі әрбір координата
t
бойынша функция болып табылады:
нүктесі
x, y, z
координаталары болсын.
t
параметрінің өзгеруінен олар да өзгеріп отырады, себебі әрбір координата
t
бойынша функция болып табылады:
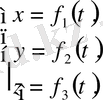
мұндағы
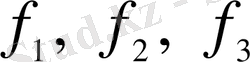 -
-
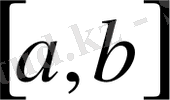 кесіндісінде берілген үздіксіз сандық функциялар (3 - сурет) .
кесіндісінде берілген үздіксіз сандық функциялар (3 - сурет) .

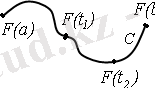
2 - сурет.
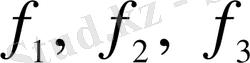 функциялары
F
параметризациясын тұтастай қамтып, оның координаталық функциясы деп аталады.
функциялары
F
параметризациясын тұтастай қамтып, оның координаталық функциясы деп аталады.
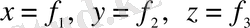 сәйкестіктерін параметрленген
С
түзуінің теңдеуі деп аталады.
сәйкестіктерін параметрленген
С
түзуінің теңдеуі деп аталады.

3 - сурет. 4 - сурет.
Егер
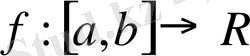 - үздіксіз функция болса, онда оның графигі параметрленген
- үздіксіз функция болса, онда оның графигі параметрленген
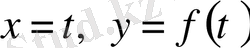 жазықтықтағы элементар сызық болады.
С
сызығы қалайша
жазықтықтағы элементар сызық болады.
С
сызығы қалайша
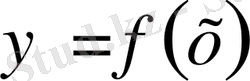 теңдеуімен байланысты. Сызықтың осылайша берілуі айқын деп аталады (4 - сурет) . Кеңістіктегі сызық
теңдеуімен байланысты. Сызықтың осылайша берілуі айқын деп аталады (4 - сурет) . Кеңістіктегі сызық
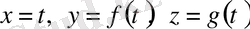 түріндегі пераметрлікпен берілетін болса, ол айқын берілген болады.
түріндегі пераметрлікпен берілетін болса, ол айқын берілген болады.
Мұндай сызық келесі параметрлікпен де берілуі мүмкін:
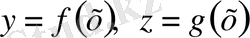 .
.
Кезкелген сызық айқын түрде берілмейді.
Айталық, шеңберді кезкелген 180 0 -тан артық доғасы айқын берілмейді.
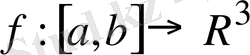 С
сызығының параметризациясы, ал
С
сызығының параметризациясы, ал
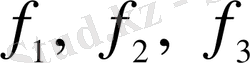 - оның координаталық функциялары болсын. F параметризациясы регулярлық деп аталады, егер, біріншіден,
- оның координаталық функциялары болсын. F параметризациясы регулярлық деп аталады, егер, біріншіден,
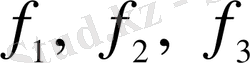 функциялары майда, екіншіден,
функциялары майда, екіншіден,
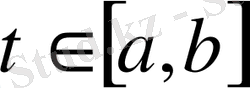 параметрінің әрбір мәнінде осы функциялардың туындысының тым болмағанда
параметрінің әрбір мәнінде осы функциялардың туындысының тым болмағанда
5 - сурет
біреуі нолге айналып кетпесе. Регулярлық параметрлігі болатын сызықтар майда деп аталады (5 - сурет) .
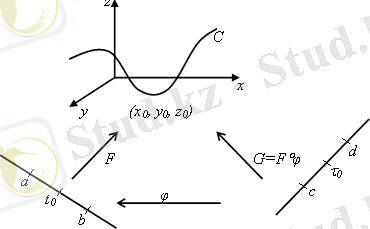
6 - сурет.
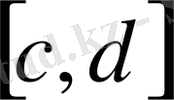 кесіндіснің
кесіндіснің
 кесіндісіндегі монотонды бейнеленуін қарастырайық. Егер
кесіндісіндегі монотонды бейнеленуін қарастырайық. Егер
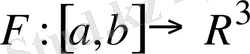 С
сызығының параметрленуі болса,
С
сызығының параметрленуі болса,
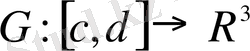 бейнеленуі де
бейнеленуі де
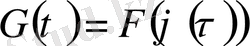 формуласымен берілген
С
сызығының параметрленуі болады.
формуласымен берілген
С
сызығының параметрленуі болады.
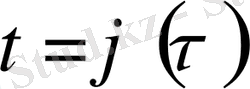 араметрін қоя отырып
F
параметризациясын аламыз. Егер
араметрін қоя отырып
F
параметризациясын аламыз. Егер
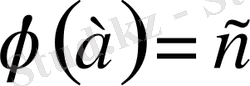 және
және
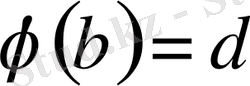 болса, онда
болса, онда
 монотонды өспелі функция, ал егер
монотонды өспелі функция, ал егер
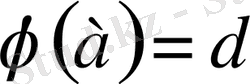 және
және
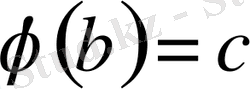 , онда
, онда
 монотонды кемімелі функция (6 - сурет) .
монотонды кемімелі функция (6 - сурет) .
Әрбір параметрлеу сызықтың бойындағы нүктелердің ретін анықтайды. Егер екі параметрлеу өспелі параметрінінң ауысуымен анықталса, онда олар бір ғана ретті анықтайды, ал егер кемімелі параметрлерді ауысуымен байланыста болса, онда әртүрлі болады. Нүктелердің ретін сызықта бекіту үшін сызқтың бастапқы және ақырғы нүктесін көрсету жеткілікті.
Шеткі нүктелері көрсетілген элементар сызықтард ы ориентацияланған деп атайды. Ориентацияланған әрбірсызықтың кезкелген доғасы ориентацияланған болады. Ориентациясының бағытын стерелкамен көрсеткен ыңғайлы (7 - сурет) .
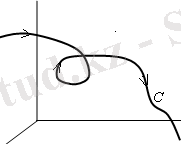
7 - сурет
1. 2 Жазықтықтағы және кеңістіктегі күрделі сызықтар
Жазықтықтағы және кеңістіктегі сызықтар мен олардың ерекшеліктерімен таныс болдық. Енді сызықтардың күрделі түрлеріне көшейік. Күрделі сызықтар өзінің салу және күрделі теңдеулерінің құрылумен ерекшеленеді. Оларға жеке-жеке тоқталып зерттейік:
- Бернулли Лемнискатасы. 1694ж Яков Бернуллитеңдеуімен берілген қисықты енгізді. Ол қисықтың сызбасын 8 санына ұқсатады. «Лемниск» грек тілінен аударғанда байлам деп аударылады. Осыдан лемниската атанып кетті. Лемниската 1718 жылдан бастап кең түрде пайдалана бастады. Бірақ лемниската Бернулли деп тек 1806ж атана бастады.
Анықтама. Берілген F 1 F 2 =2c кесіндісінің ұштарына дейінгі аралықтардың көбейтіндісі c 2 -ға тең болатын нүктелердің геометриялық орны. Мұндағы F 1 , F 2 нүктелері лемниската фокустары деп аталады. F 1 F 2 түзуі оның осі.
Тікбұрышты жүйедегі канондық теңдеуі ( О - F 1 F 2 кесіндісінің ортасы, OX осі F 2 F 1 бойлаған)
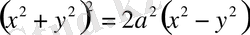
Полярлық жүйедегі теңдеуі ( О - полюс, ОХ - полярлық ось)
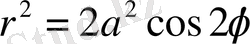
φ
бұрышы
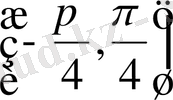 және
және
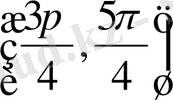 аралықтарында өзгереді.
аралықтарында өзгереді.
Рационалдық параметрлік теңдеуі
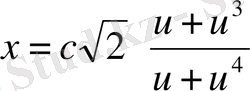 ,
,
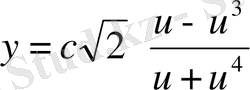
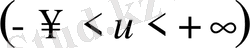
мұндағы
u
параметрі
φ
-мен келесі тәуелділікте
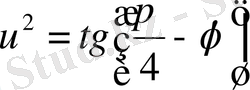
8 - сурет. Бернулли Лемнискатасының сызбасы
Сызықты салуда Кассини сызығын салудың ортақ әдісін пайдалануға болады, бірақ төмендегі тәсіл (К. Маклорен) ыңғайлырақ және жеңілірек. Центрі
F
1
(немесе
F
2
) болатындай
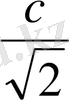 радиусын алып шеңбер сызамыз. Кезкелген
OPQ
қиюшы түзу саламыз, оның бойынан
PQ
хордасына тең болатын
OM
және
OM
1
кесінділерін өлшеп саламыз.
М
нүктесі лемнискатаның бір бөлігін сызып шығады,
М
1
екіншісін.
радиусын алып шеңбер сызамыз. Кезкелген
OPQ
қиюшы түзу саламыз, оның бойынан
PQ
хордасына тең болатын
OM
және
OM
1
кесінділерін өлшеп саламыз.
М
нүктесі лемнискатаның бір бөлігін сызып шығады,
М
1
екіншісін.
Ерекшелігі: сызықтың екі симметрия осі бар -
F
1
F
2
(OX)
және
OY⊥OX
. Лемнискатаның
А
1
,
А
2
нүктелері
О
нүктесінен ең алыс орналасқан және
F
1
F
2
осінде
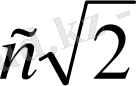 қашықтықта жатыр.
қашықтықта жатыр.
- Логарифмдік спираль. Сызықты алғаш рет 1638ж Р. Декарт ерекшелігін байқап зерттей бастаған. Қатарынан сол уақытта Э. Торричелли Декаттан тәуелсіз және тереңірек геометриялық спиральдің қасиеттерін зерттеген. Торричелли ғажайып спиральдың көптеген қасиеттерін дәлелдеді. Сызыққа «логарифмдік спираль» атын 1704 жылы П. Вариньон берген болатын. Себебі полярлық радиустардың арасындағы бұрыш олардың қатынастарының логарифміне пропорционал.
Анықтама. UV түзуі O нүтесіне бекітіліп, сол нүктеде (полюс) бір қалыпты айналсын, ал M нүктесі O нүктесінен OM -ге пропорционал жылдамдықпен алыстай берсін, . M нүктесімен сызылған қисықты логарифмдік спираль дап атайды.
Егер М нүктесінің О полюсінан алыстауы UV түзуінің айналуы сағат тілімен бағыттас болса, онда логарифмдік спираль оң, кері жағдайда - теріс болып табылады. Оң спираль үшін q>1 ; теріс спираль үшін q<1 . q=1 болғанда спираль шеңберге ауысады.
Оң логарифмдік спиральды салу үшін осі кооэффициентін
q
деп алып,
О
центрі болатын кезкелген шеңберді сағат тіліне қарама-қарсы бағытта
В
1
, В
2
, В
3
, . . . ,
нүктелері болатындай
 бөлікке бөледі. Анық болу үшін
бөлікке бөледі. Анық болу үшін
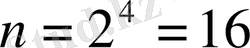 деп алайық.
ОВ
0
сәулесінің бойынан кезкелген
А
0
нүктесін алып,
OA
1
=qOA
0
кесінділерін саламыз
. OA
1
кесіндісін диаметрі деп алып
O
/
шеңберін саламыз және
К
нүктесінде шеңбермен қиылысатындай етіп
A
0
К ⊥ OA
1
түзуін саламыз.
ОК
радиусты шеңбер
OB
8
сәулесін
D
8
нүктесінде қиып өтеді; ол шеңбер
L
нүктесінде
OA
1
сәулесін де қиып өтеді.
O
/
шеңберімен
K
/
нүктесінде қиылысатындай
LК ⊥ OA
1
түзуін жүргіземіз.
OK
/
радиусты шеңбер
OB
12
сәулесін
D
12
нүтесінде қиып, ал
OA
1
сәулесін
L
/
нүктесінде қиып өтеді. Ол арқылы тағы да
L
/
К
//
⊥ OA
1
жүргіземіз т. с. с. Нәтижесінде
D
14
және
D
15
нүктелерін аламыз.
деп алайық.
ОВ
0
сәулесінің бойынан кезкелген
А
0
нүктесін алып,
OA
1
=qOA
0
кесінділерін саламыз
. OA
1
кесіндісін диаметрі деп алып
O
/
шеңберін саламыз және
К
нүктесінде шеңбермен қиылысатындай етіп
A
0
К ⊥ OA
1
түзуін саламыз.
ОК
радиусты шеңбер
OB
8
сәулесін
D
8
нүктесінде қиып өтеді; ол шеңбер
L
нүктесінде
OA
1
сәулесін де қиып өтеді.
O
/
шеңберімен
K
/
нүктесінде қиылысатындай
LК ⊥ OA
1
түзуін жүргіземіз.
OK
/
радиусты шеңбер
OB
12
сәулесін
D
12
нүтесінде қиып, ал
OA
1
сәулесін
L
/
нүктесінде қиып өтеді. Ол арқылы тағы да
L
/
К
//
⊥ OA
1
жүргіземіз т. с. с. Нәтижесінде
D
14
және
D
15
нүктелерін аламыз.
B
0
B
8
,
B
1
B
9
түзулерінің бойында жатқан спиральдің шексіз нүктелерін келесі түрмен анықтауға болады.
D
14
нүктесіндегі
 OD
14
Q
бұрышы
OD
15
D
14
бұрышына тең болатын бұрыштар салынады;
OB
13
сәулесімен қиылысқанда
D
13
ізделінді спиральдың нүктесін аламыз.
A
1
нүктесіндегі
OD
14
Q
бұрышы
OD
15
D
14
бұрышына тең болатын бұрыштар салынады;
OB
13
сәулесімен қиылысқанда
D
13
ізделінді спиральдың нүктесін аламыз.
A
1
нүктесіндегі
 OA
1
Q
/
=
OA
1
Q
/
=
 OD
15
A
1
саламыз;
OB
1
сәулесімен қиылысқаннан
E
1
нүктесін саламыз және т. с. с.
OD
15
A
1
саламыз;
OB
1
сәулесімен қиылысқаннан
E
1
нүктесін саламыз және т. с. с.
9 - сурет. Логарифмдік спираль
Полярлық координатадағы теңдеуі (полюс спиральдің полюсімен сәйкес келеді; полярлық ось спиральдың М0 кезкелген нүкте сі арқылы жүргізілген) :
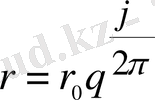
мұндағы r 0 = OM 0 - M 0 нүктесінің полярлық радиусы, ал q - өсу коэффициенті.
Әдетте бұл теңдеу келесі түрде беріледі
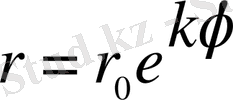 ,
,
мұндағы
k
- өсу коэффициенті
q
арқылы өрнектелген параметр:
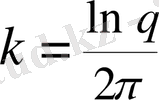
Керісінше,
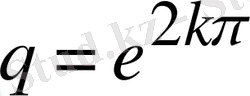
k параметрінің геометриялық мағынасы келлесі теңдігінен шығады
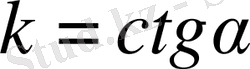
мұндағы
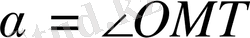 -
ОМ
түзуі мен
МТ
жанаманың арасындағы бұрыш. Оң спираль үшін
k
параметрінің мәні - оң, теріске - теріс.
-
ОМ
түзуі мен
МТ
жанаманың арасындағы бұрыш. Оң спираль үшін
k
параметрінің мәні - оң, теріске - теріс.
- Аньеза Верзьера (Локон Аньези) . теңдеуімен берілген сызық 17 ғасырдың 30-шы жылдарындағы П. Ферма еңбектерінде көптеп кездеседі. Верзьераның салу тәсілі мен қасиеттерін 1718 жылы итальян ғалымы Гвидо Гранди ұсынған. «Верзьера» атауын да енгізген Гвидо болатын.
Анықтама. АО = a кесіндісін диаметрі ретінде алып шеңбер салайық және ВС хордасы BM:BC=OA:OB пропорциясы бойынша М нүктесіне дейін созылсын. C нүктесі арқылы OC 1 C 2 шеңбері жүргізілсе M нүктесі арқылы Аньеза верзьера аты қисықты сызып шығады. Сызықтың түбегелі зерттеп, негіздеген Мария Гаэтана Аньези итальян ғалымының есімімен байланысты.
10 - сурет. Аньеза Верзьера
Теңдеуі. ( О - басы, Х / Х кез келген шеңбердің абсцисса осіндегі О нүктесіне жүргізілген жанамасы)
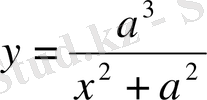
Параметрлік теңдеуі
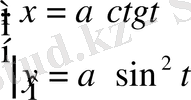
М. Г. Аньези верзьераны сызудудың келесі әдісін ұсынған. OC және UV түзулерінің қиылысу нүктесі L берілген шеңбермен A нүктесінде жанасады. LMllAO және CBllAL түзулерін сызамыз. LM және CB түзулері M нүктесінде қиылысады. Сызбасын салуды сызықтың ерекшеліктерін ескеру қажет.
Сызықтың ерекшеліктерімен таныс болайық:
ОА
диаметрі - верзьераның симметрия осі. Ол тұтастай
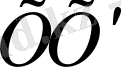 түзуінің бір жақ жазықтығында орналасқан. Верзьераның екі бүгілу нүктелері бар:
түзуінің бір жақ жазықтығында орналасқан. Верзьераның екі бүгілу нүктелері бар:
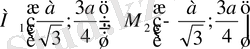 .
М
2
F, M
2
F
жанамаларының
X
/
X
осьтерімен жасайтын бұрыштарды
.
М
2
F, M
2
F
жанамаларының
X
/
X
осьтерімен жасайтын бұрыштарды
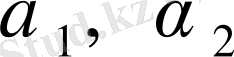 келесі формулалармен есептеуге болады:
келесі формулалармен есептеуге болады:
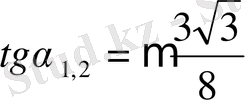 .
М
2
F, M
2
F
жанамаларын салу үшін
ОА
диаметріне
.
М
2
F, M
2
F
жанамаларын салу үшін
ОА
диаметріне
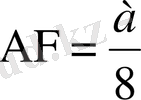 кесіндісін салу жеткілікті.
кесіндісін салу жеткілікті.
- Кардиоида.
11 - сурет. Кардиоида
Анықтамасы. Радиусы
а
болатын шеңбердің бойындағы
О
және
А
нүктелері арқылы сәуле жүргізілген.
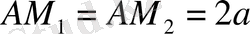 қатынасын қанағаттандыратын
М
нүктелерінің геометриялық орны кардиоида болып табылады.
қатынасын қанағаттандыратын
М
нүктелерінің геометриялық орны кардиоида болып табылады.
Тікбұрышты жүйедегі теңдеуі (координатал басы - О полюсінде; ОХ осі ОВ сәулесінің боймен бағытталған) :
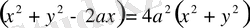
Полярлық жүйедегі теңдеуі ( О - полюс; ОХ - полярлық ось) :
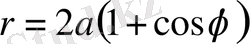
Параметрлік теңдеуі
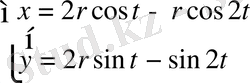
- Диоклес Циклоидасы. Диоклес б. з. д. 2 ғасырда өмір сүрген ежелгі грек ғалымы. Сызықты зерттеу мен ерекшеліктерін айқындау жолында көптеген еңбектері үшін циклоида - диоклес циклоидасы атына ие болған.
12 - сурет. Диоклес циклоидасы
ОА=2a кесіндісін диаметрі ретінде алып С шеңберін сызайық (12 - сурет) және А нүктесі арқылы UV жанамасын жүргіземіз. О нүктесі арқылы өтетін кезкелген ОF , ол UV мен F нүктесінде, Е нүтесінде С шеңберімен қиылысады. ОЕ хордасына тең болатындай етіп, OF түзуінің бойынан F -дан O -ға қарай FM кесіндісін саламыз. OF түзінің бұрылғандағы M нүктесінің сызып өтетін қисығын Диоклес циклоидасы деп атаймыз.
Координаталық жүйедегі теңдеуі ( О -басы, ОХ - абсцисса осі)
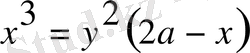
Полярлық жүйедегі теңдеуі ( О - полюс, ОХ - полярлық ось)
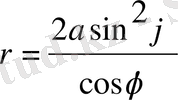
Рационалдық параметрлігі
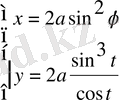 немесе
немесе
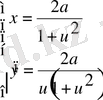 мұндағы
u = tgφ
мұндағы
u = tgφ
- Конхоида Никомеда. Никомед б. д. д. 250-150ғ. ғ. өмір сүрген ежелгі грек ғалымы. Сызықты қабыршаққа ұқсас болғандықтан конхоида деп атаған.
Қазір белгілі болғандай бұл есеп сызғыш пен циркульдің көмегімен бұрышты таңдай отырып салуға болады. Бұл қисықтың сызбасын салу үшін Никомед арнайы конхоидограф атты сызу құралын құрастырған.
13 - сурет.
O нүктесі (полюс), UV түзуі (табаны) және l кесіндісі берілсін. O полюсінен N түзуімен қиылысатындай етіп кезкелген ON түзуін жүргіземіз. ON түзуінің бойынан N -нан екі жағына қарай NM 1 =NM 2 =l кесінділер саламыз. M 1 және M 2 нүктелерінің геометриялық орнын Конхоида Никомеда деп аталады. Конхоиданың ON түзуінің бойындағы N ( М 1 нүктесмен сызғанда) нүктесінен кейін орналасқан сызықты конхоиданың сыртқы бөлігі, М 2 нүктесмен сызғандағы бөлігің ішкі бөлігі болып табылады.
Тікбұрышты жүйедегі теңдеуі (координаталар басы - О полюсінде; абсциисса осі ОВ сәулесімен бағытталған, В нүктесі - полюстің табанына проекциясы)
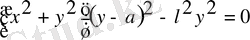
Полярлық жүйедегі теңдеуі
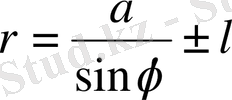
Параметрлік теңдеуі
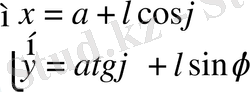
- Төртжапырақшалы раушан (четырехлепестковая роза) .
Тікбұрышты координаталық жүйедегі теңдеуі
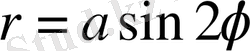
Параметрлік теңдеуі
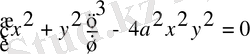
- Конондық спираль.
Анықтамасы. ОL түзуі перпендикуляр борлмайтын Oz осін тұрақты ω бұрыштық жылдамдығымен бірқалыпты айналады. M нүтесі OL түзуімен жылжиды: а) O нүктесіне дейінгі жылжымалы нүктеге дейінгі OM аралығына пропорционал жылдамдық; б) тұрақты жылдамдықпен; Бірінші жағдайда М нүктесі конондық спиралды, екіншісінде - конондық винттік сызықты шығып өтеді.
Параметрлік теңдеуі
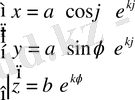 , мұндағы
, мұндағы
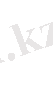
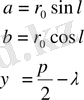
Егер конондық спиральды жазықтыққа жинақтайтын болсақ, бұрындары зерттеліп жүрген спиральды алуға болады. Конондық спиральдың ерекшелігі де осыда.
- Бицилиндрика.
Анықтама. Радиустары a және b болатын екі цилиндрдің остері тікбұрыш жасап қиылысады. Цилиндрлердің қиылысуынан пайда болған екі тұтас сызықтан құралады, бұл тұтастық бицилиндрика деп аталады.
Тікбұрышты жүйедегі теңдеуі
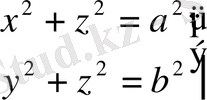
Параметрлік теңдеуі
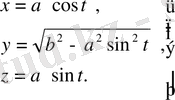
Бициллиндрика атауы айтып тұрғандай екі цилиндрдіңқиылысуынан пайдаболғандықтан сызбасы өте оңай сызылады. a=b болған жағдайда бицилиндрика екі эллипсқа айналады.
14 - сурет. Конондық спираль 15 - сурет. Бицилиндрика
2 КҮРДЕЛІ СЫЗЫҚТАРДЫҢ ҚИСЫҚТЫҚТАРЫН ЕСЕПТЕУ
2. 1 Қисықтықты есептеу теориясы
Сызықтардың басты ерекшеліктерінің бірі оладың қисықтықтарының шамасының бар болуы, яғни қисықтықты есептеудің арнайы ережелері мен әдістері қалыптасқан. Қисықтықты есептеуден бұрын доға ұғымымен және оның сызықтағы алатын орны жайлы мәлімет алайық.
- g кесіндінің f топологиялық бейнеленуінің көрінісі болып табылады. Г сынығына қатысты (16 - сурет) біз сызығы дұрыс салынған деп есептейтін болмыз. Сынықтың қасиеттерінің бірі сызыққа тәуелсіз дұрыс салыну болып табылады. Доғаның ұзындығы деп бұл доғаға дұрыс сызылған сынықтың ұзындығын айтамыз.
16 - сурет .
Теорема. Жазық сызық - түзетілетін сызық. Егер
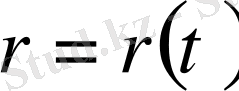 оның жазық параметрленуі және
оның жазық параметрленуі және
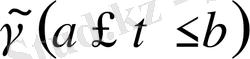 - сызығының бөлігі болса, онда
- сызығының бөлігі болса, онда
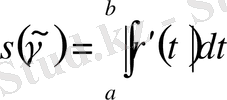
бұл бөліктің ұзындығы.
Дәлелдеуі.
Р
- сызықтың кезкелген нүктесі болсын және
r=r(t)
осы нүктеге байланысты параметрленген сызық.
Г
сынығының
Р
нүтесінің маңындағы
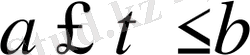 кесінің ұзындағын айқындайық.
кесінің ұзындағын айқындайық.
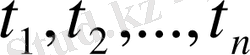 - сынық сызықтың төбелеріне байланысты параметрлігі.
- сынық сызықтың төбелеріне байланысты параметрлігі.
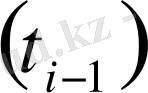 және
және
 төбелерін біріктіретін сынықтың ұзындығы
төбелерін біріктіретін сынықтың ұзындығы
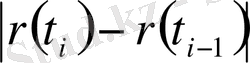 тең. Сынықтың бүкіл ұзындығы:
тең. Сынықтың бүкіл ұзындығы:
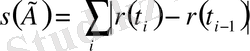
Алатынымыз
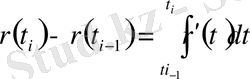 .
.
Бұдан
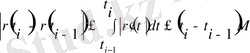
мұндағы М -
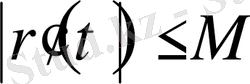 шартын қанағаттандыратын тұрақты. Шығатыны,
шартын қанағаттандыратын тұрақты. Шығатыны,
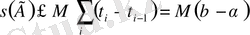 .
.
Г сынығы Р нүктесінің маңындағы азғана бөлікте орналасқан, яғни сызығы түзетіледі.
Келесі теңдеумен берілген сызығының
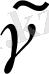 кесіндісінің ұзындығын табайық
кесіндісінің ұзындығын табайық
r=r(t)
,
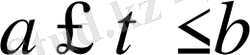 .
.
Біріншіден, алдынғы тұжырымды ескере отырып,
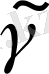 кесіндісіне енгізілген сынықтардың ұзындықтарының шектеулі екенін анықтаймыз. Бұдан,
кесіндісіне енгізілген сынықтардың ұзындықтарының шектеулі екенін анықтаймыз. Бұдан,
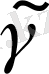 кесіндісінің доға ұзындығы шектеулі.
кесіндісінің доға ұзындығы шектеулі.
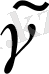 кесіндісіне келесі шарттарды қанағаттандыратын
Г
сынығын енгізейік: 1)
Г
сынығының ұзындығы
кесіндісіне келесі шарттарды қанағаттандыратын
Г
сынығын енгізейік: 1)
Г
сынығының ұзындығы
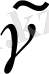 кесіндісінің доға ұзындығынан
кесіндісінің доға ұзындығынан
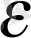 артық; 2) барлық
і
үшін
артық; 2) барлық
і
үшін
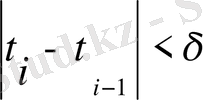 . Мұндағы
. Мұндағы
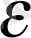 және
және
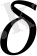 - кезкелген оң сандар. Осындай сынықтың бар болуын көру қиын емес. Негізінде, бірінші шартты қанағаттандыратын
Г
сынығы бар. Оны жаңа төбелермен қотылтырғанмен бірінші шартты бұзбаймыз. Сонымен қатар төбелерді қосу арқылы екінші шартты да қанағаттандыруға болады. Ендігі сынықтың бастапқы нүктесі
(а),
ал ақырғысы
(b)
деп алуға болады.
- кезкелген оң сандар. Осындай сынықтың бар болуын көру қиын емес. Негізінде, бірінші шартты қанағаттандыратын
Г
сынығы бар. Оны жаңа төбелермен қотылтырғанмен бірінші шартты бұзбаймыз. Сонымен қатар төбелерді қосу арқылы екінші шартты да қанағаттандыруға болады. Ендігі сынықтың бастапқы нүктесі
(а),
ал ақырғысы
(b)
деп алуға болады.
Алатынымыз
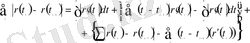 (1)
(1)
Бұл теңдіктің сол жағы
Г
-ның құрылымы
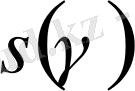 -дан
-дан
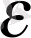 -ға ғана артықшылығы бар. Оң жағын қарастыратын болса, ол
-ға ғана артықшылығы бар. Оң жағын қарастыратын болса, ол
 -ға жақындай береді. Шынында да, оң жағаның екінші бөлігі
-ға жақындай береді. Шынында да, оң жағаның екінші бөлігі
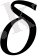 -мен қоса интегралдың анықтамасы бойынша кіші. Үшінші бөлігі келесідей
-мен қоса интегралдың анықтамасы бойынша кіші. Үшінші бөлігі келесідей
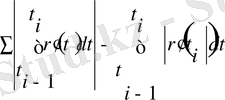
және бұдан абсолют шамадан аспайды
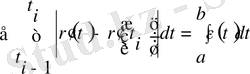
мұндағы
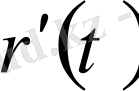 функциясының үздіксіздігінен
функциясының үздіксіздігінен
 болғанда
болғанда
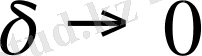 . Сонымен (1) теңдігінің үшінші бөлігі
. Сонымен (1) теңдігінің үшінші бөлігі
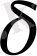 -мен бірге аз.
-мен бірге аз.
Сонымен
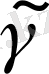 кесіндісің ұзындығы сызығынан айырмашылығы аз болады
кесіндісің ұзындығы сызығынан айырмашылығы аз болады
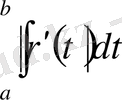 және оған тең болады.
және оған тең болады.
Теорема дәлелденді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz