Математика және музыка

Мазмұны

КІРІСПЕ 3

І ТАРАУ. ДЫБЫСТЫҚ ҮЙЛЕСІМДІЛІК ... ... ... ... ... ... ... ... ... ... ... ... ..5

ІІ ТАРАУ. ТЕРМИНОЛОГИЯ. 9
1 БӨЛІМ. ТІЗБЕКТЕР ЖӘНЕ ПАРАЛЛЕЛЬДЕР 9
2 БӨЛІМ. РИТМДЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...12
3 БӨЛІМ. МУЗЫКАДАҒЫ ЛОГАРИФМДЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ..15
4 БӨЛІМ. МУЗЫКАДАҒЫ "ЖАТТЫҒУЛАР" ... ... ... ... ... ... ... ... ... ... ... ... ... .17

ІІІ ТАРАУ. ҰТЫМДЫЛЫҚ ЖӘНЕ АФФЕКТ 21

ҚОРЫТЫНДЫ 24

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР 25

Кіріспе
Математика және музыка – адам мәдениетінің екі полюсі, екі мектеп пәні, екі ойлау жүйесі. Математика сандардың реттелген және шектеусіз кеңістігімен, логикалық ойлаумен тығыз байланысты. Музыка елестетумен, қиялмен, көпжақты және көптүсті музыка әуенімен және өмірді қабылдауымен, сонымен бірге құпия және шексіз дыбыстар әлемімен байланысты. Музыка көптүрді, ал математика жалғыздықты қабылдайды. Музыка сезімге, жанға, математика ақыл-еске әсер етеді. Алайда, математика абстракт ғылым екеніне, ал музыка өнердің жеке түрі екеніне қарамастан математика және музыканың байланысы тарихи және іштей қалыптасқан.
Бұл байланысты математика және музыканының «белгілеулерінде» табуға болады.
Адамның мақсаты - әлемді тану, ал сенімде - әлемнің ақиқаты. Әдетте адам тас білімді, жансыз машина емес, оған логикаға бағынбайтын нәрсе қатысады («бұны» әдемі сөзбен иррациональдық деп айтуға болады). Бірақ, заттық әлемнің әрбір нәрсесі сезімдік жүкті арқалайтындықтан «аяқ астындағы негізсіз» өмірді елестету мүмкін емес, демек рациональдықсыз болмайды. Басқаша айтқанда, адам рациональды немесе иррациональды өмір сүре алмайды. Бірінші жағдайда, әлемдік құрылғының логикаға сәйкесіздігін сезінуден және әлеммен осы ауыртпашылықты сезінуден, ал екінші қоршаған ортада оның тағы табиғи болмысына қайшы болатын жазық материалды, затты және қатты заттың бөлінбейтін бөлігін сезіну. Адамның әлеммен түсінбеушілігі сенім мен логиканың әртүрлілігінен еріксіз басталады.
Адамның рациональдық бөлігін бағалай отырып, техника, физика, химия және математика көмегімен әлемнің рационал бөлігін тану үшін жаралған деп айтуға болады. Математика барлық тану құралдарының әмбебап жабдығы болады, себебі ол қосымшаны, деректі емес, басқа ғылымдар қолданатын идеяны қарастырады.
Менің көзқарасымша музыка барлық өнер түрлерінен «керемет», себебі ол адам сезіміне тікелей әсер етеді, демек оның иррационал бөлігіне.
Жоғарыда айтылғандардан мынадай қорытындыға келуге болады, егер адам бір немесе басқа бөлігімен өмір сүре алмаса, демек бөлік оларды танудың нақты құралдарын бөлуге болмайтын сияқты, бір-бірінсіз өмір сүре алмайды, бұдан адамда музыка және математика мәңгі бірге екені шығады. Атап айтқанда, адам ойланатын, баға беруге ұмтылатын және барлығына түсінік беретіндей тірі жан, шынымен бағалады және музыка мен математика арасындағы байланысты тапты.
Математиканың маңызы қазір үздіксіз өсіп келеді. Математикада жаңа идеялар мен әдістер туындап келеді. Бұлардың бәрі математиканы қолдану салаларының мааематиканы айтарлықтай қолданылмайтыны жоқ.
Көбінесе мектеп оқушыларында математика тек сандар және өлшеулермен шұғылданады деген әсер қалады. Бірақ, математика есепшілер мен есептеушілерге ғылым ғана емес, бұл анағұрлым артық нәрсе. Негізінен, математиканың ұғым арасындағы сапалы қатынаспен логикамен байланысы бар.
Мұғалім бағдарламасындағы сабақта әрқашанда элементар математиканың көптеген маңызды және қызықты сұрақтарға тоқтала беру мүмкіндігі бола бермейді. Сондықтан, сыныптан тыс жұмыс қажет екені айқын.
«Математика және музыка» тақырыбындағы жобаның мақсаты жан-жақтың математика заңына бағынатынын көрсету, дербес жағдайда, музыка дамуындағы математикалық маңызын көрсету. Ежелгі грек математигі, философ, астроном Пифагор оқушылардың 8 сыныпта танысатын теоремасының музыкалық сауаттылық негізін қалады. «Математика және музыка» тақырыбындағы жоба Пифагордың ғылыми ашуларына: сандар гармониясының теориясы, музыка теориясы, ашылуына қатысты сұрақтарды бейнелейді.
Жобамен жұмыс істеу үшін «математикаға не үшін музыка керек?» деген негізгі сұрақ қойылды. Бірінші кезеңде сұраққа талқылау жүргізілді. Оқушы өз ойын айтты. Мұғалім өз алдына оқушыларды Пифагор тұжырымдамасымен таныстырады. [2]

Қолданылған әдебиеттер

[1] Лиман М. М. «Оқушыларға математика және математиктер жайлы»,
Алматы «Мектеп», 1984.
[2] Азевич А. И. «В тональности ми мажор».
[3] Шамин Р. «ММ – тождественны всем»
[4] Варга Б., Димень, Ю., Лопариц Э. «Язык, музыка, математика».
[5] Перельман Я. И. «Қызықты математика», Алматы, «Мектеп», 1986.
[6] Хельга де ля Мотт-Хабер. «Рациональность и аффект».
[7] Волошинов А. В. Пифагор. М. : Просвещение, 1993.
[8] Гарднер М. Путешествие во времени. М.: Мир, 1990.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

Бағыты: Экономикалық және әлеуметтік процестерді
математикалық модельдеу

Секция: Қолданбалы математика

Тақырыбы:
Математика және музыка

Мазмұны

КІРІСПЕ 3

І ТАРАУ. Дыбыстық
үйлесімділік ... ... ... ... ... ... ... ... ... ... ... ... ...5

ІІ ТАРАУ. Терминология. 9

1 бөлім. Тізбектер және параллельдер 9
2 бөлім.
Ритмдер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ..12
3 бөлім. Музыкадағы
логарифмдер ... ... ... ... ... ... ... ... ... ... ... ... ... ..15
4 бөлім. Музыкадағы "жаттығулар"
... ... ... ... ... ... ... ... ... ... ... ... ... ..17

ІІІ ТАРАУ. ұтымдылЫҚ ЖӘНЕ аффект 21

ҚОРЫТЫНДЫ 24

ҚОЛДАНылҒАН ӘДЕБИЕТТЕР 25

Математика барлық ғылымдардың тұңғышы және
оларға пайдалы да, қажет те.
Басқа ғылымдарды... математикалық
дәлелдемелер арқылы тани білу керек. Бұл
математикалық дәлелдемелерсіз өзге ғылымдарды
түсінуге де, түсіндіруге де болмайды, онсыз
ол ғылымдарды оқып үйренуге де, үйретуге де
болмайды. Егер біреу, математиканың күшін
жекелеген ғылымдарға қолданып, дербес
мәселелерге көшсе, онда ол математикасыз
(математиканы қолданбай) білім шыңына шыға
алмайды. [1]

Бэкон Р.

Кіріспе

Математика және музыка – адам мәдениетінің екі полюсі, екі мектеп пәні,
екі ойлау жүйесі. Математика сандардың реттелген және шектеусіз
кеңістігімен, логикалық ойлаумен тығыз байланысты. Музыка елестетумен,
қиялмен, көпжақты және көптүсті музыка әуенімен және өмірді қабылдауымен,
сонымен бірге құпия және шексіз дыбыстар әлемімен байланысты. Музыка
көптүрді, ал математика жалғыздықты қабылдайды. Музыка сезімге, жанға,
математика ақыл-еске әсер етеді. Алайда, математика абстракт ғылым екеніне,
ал музыка өнердің жеке түрі екеніне қарамастан математика және музыканың
байланысы тарихи және іштей қалыптасқан.
Бұл байланысты математика және музыканының белгілеулерінде табуға
болады.
Адамның мақсаты - әлемді тану, ал сенімде - әлемнің ақиқаты. Әдетте
адам тас білімді, жансыз машина емес, оған логикаға бағынбайтын нәрсе
қатысады (бұны әдемі сөзбен иррациональдық деп айтуға болады). Бірақ,
заттық әлемнің әрбір нәрсесі сезімдік жүкті арқалайтындықтан аяқ астындағы
негізсіз өмірді елестету мүмкін емес, демек рациональдықсыз болмайды.
Басқаша айтқанда, адам рациональды немесе иррациональды өмір сүре алмайды.
Бірінші жағдайда, әлемдік құрылғының логикаға сәйкесіздігін сезінуден және
әлеммен осы ауыртпашылықты сезінуден, ал екінші қоршаған ортада оның тағы
табиғи болмысына қайшы болатын жазық материалды, затты және қатты заттың
бөлінбейтін бөлігін сезіну. Адамның әлеммен түсінбеушілігі сенім мен
логиканың әртүрлілігінен еріксіз басталады.
Адамның рациональдық бөлігін бағалай отырып, техника, физика, химия
және математика көмегімен әлемнің рационал бөлігін тану үшін жаралған деп
айтуға болады. Математика барлық тану құралдарының әмбебап жабдығы болады,
себебі ол қосымшаны, деректі емес, басқа ғылымдар қолданатын идеяны
қарастырады.
Менің көзқарасымша музыка барлық өнер түрлерінен керемет, себебі ол
адам сезіміне тікелей әсер етеді, демек оның иррационал бөлігіне.
Жоғарыда айтылғандардан мынадай қорытындыға келуге болады, егер адам
бір немесе басқа бөлігімен өмір сүре алмаса, демек бөлік оларды танудың
нақты құралдарын бөлуге болмайтын сияқты, бір-бірінсіз өмір сүре алмайды,
бұдан адамда музыка және математика мәңгі бірге екені шығады. Атап
айтқанда, адам ойланатын, баға беруге ұмтылатын және барлығына түсінік
беретіндей тірі жан, шынымен бағалады және музыка мен математика арасындағы
байланысты тапты.
Математиканың маңызы қазір үздіксіз өсіп келеді. Математикада жаңа
идеялар мен әдістер туындап келеді. Бұлардың бәрі математиканы қолдану
салаларының мааематиканы айтарлықтай қолданылмайтыны жоқ.
Көбінесе мектеп оқушыларында математика тек сандар және өлшеулермен
шұғылданады деген әсер қалады. Бірақ, математика есепшілер мен
есептеушілерге ғылым ғана емес, бұл анағұрлым артық нәрсе. Негізінен,
математиканың ұғым арасындағы сапалы қатынаспен логикамен байланысы бар.
Мұғалім бағдарламасындағы сабақта әрқашанда элементар математиканың
көптеген маңызды және қызықты сұрақтарға тоқтала беру мүмкіндігі бола
бермейді. Сондықтан, сыныптан тыс жұмыс қажет екені айқын.
Математика және музыка тақырыбындағы жобаның мақсаты жан-жақтың
математика заңына бағынатынын көрсету, дербес жағдайда, музыка дамуындағы
математикалық маңызын көрсету. Ежелгі грек математигі, философ, астроном
Пифагор оқушылардың 8 сыныпта танысатын теоремасының музыкалық сауаттылық
негізін қалады. Математика және музыка тақырыбындағы жоба Пифагордың
ғылыми ашуларына: сандар гармониясының теориясы, музыка теориясы, ашылуына
қатысты сұрақтарды бейнелейді.
Жобамен жұмыс істеу үшін математикаға не үшін музыка керек? деген
негізгі сұрақ қойылды. Бірінші кезеңде сұраққа талқылау жүргізілді. Оқушы
өз ойын айтты. Мұғалім өз алдына оқушыларды Пифагор тұжырымдамасымен
таныстырады. [2]

1 Тарау. Дыбыстық үйлесімділік

Қазіргі композиторға интервал, гамма, музыкалық құрылым деген
ұғымдарсыз вокальды және аспапты музыканың шығармасын елестету қиын. Көп
ғасырлар бойы адамдар бұл сөздерді білмеуі орынды. Мұндай жағдайда мажор
және минор, аккордтар және интервалдар құрылуының бастауында кім тұрды
деген сұрақ қойылады. Ал бастауында ұлы математик Пифагор тұрды. Оның
музыка теориясы облысындағы жаңалығы музыкадағы математикалық пропорция
дамуының негізі бола алды.
Егер музыкалық аспаптың шектерінің ұзындығы бір-біріне дұрыс сандық
қатынаста болса шектерден шығатын дыбыстардың үйлесімі неғұрлым жағымды
болуы – жаңалықтың ерекшелігі.
Өз жаңалығын жүзеге асыру үшін Пифагор жартылай аспап, жартылай құрал
– монохорд қолданды. Ғалым жаппаның жоғарғы бөлігінде, соның көмегімен
шекті бөліктерге бөлуге болатын шектердің астына шкала сызды. Көп
тәжірбиелер жүргізілді, соның нәтижесінде Пифагор созылған шектің
математикалық үндесуін жазды.
Бұл сипаттамаға көшпес бұрын, дыбыстың не екенін еске түсіну керек.
Акустика бойынша дыбыс ауада толқын тәрізді таралады. Яғни, музыкалық
аспаптар ойнағаннан бастап, олардан барлық зал бойынша дыбыстық толқындар
жайыла бастайды. Ауа арқылы берілетін толқындық өзгерістер біздің құлақ
құрышымызға әсер етеді, соның нәтижесінде біз дыбысты қабылдаймыз. Ұзақ
уақыт бойы есту қабілетіне шектің жағымды дыбыс шығаруын не анықтайтыны
туралы ешқандай ортақ пікір болған жоқ (музыкада консонанс деп аталады).
Біреулер бұл шектің созылғандығына байланысты деп есептейді, басқалары
жауапты шек ұзындығынан іздейді, үшіншілері консонансты тонның көтерілуі
көмегімен анықтайды. Бұл сұрақтың айқындылығы Архитдан (IV ғ. б. э. д.)
кейін анықтады. Ол тонның көтерілуі мәнін шектің ұзындығынан да емес және
созылу күшінен де емес, оның қозғалыс жылдамдығынан көрді, яғни ауаның
бөліктеріндегі шектің екпінді жылдамдығынан.
Бүгін бұл жылдамдық шектің толқынды қозғалыс жиілігі деп аталады. Архит
тонның көтерілуі оның кері пропорционал екендігін анықтады. Архит
пифагорлік одақтың соңы болды. Оның математика және механика аймағында аты
шықты, сонымен бірге пифагорлік музыка аймағында ірі теоретик болды. Оның
музыкалық жүйесі негізінде екі ұлы ғалымның Пифагор және Архиттің
есімдерімен аталатын екі заң жатыр. Бұл заңдар мыналар:
1. Екі үн шығаратын шек консонансты анықтайды, егер олардың ұзындығы
үшбұрышты санды құрайтын бүтін санға қатысты болса, 10=1+2+3+4, яғни
1:2, 2:3, 3:4. Және n(n+1) (n=1, 2, 3) қатынасында n саны кіші болған
сайын алынатын интервалдық үндес бола береді.
2. Дыбыс шығарылған шектің толқынды қозғалыс w жиілігі оның l ұзындығына
кері пропорционал. w=al, мұндағы a – шектің физикалық қасиетін
сипаттайтын коэффициент.
Алдағы уақытта бірнеше теория ұғымы қажет болады. Дербес жағдайда,
гаммалар, тондар аралықтары, ладтар.
Гамма немесе дыбыстық қатар деп негізгі тоннан жоғарғы немесе төмен
орналасқан дыбыстардың орналасуы тізбегін атайды. Тондар арасындағы
интервал деп берілген дыбыстық қатарда жоғарғы тонның сатысының рет санының
төменгі тонға қатынасын атайды. Ал екі тонның интервалдық коэффициенті
жоғарғы толқынның төменгі жиілікке қатынасы: w1w2.
Орта ғасырда интервалда коэффициенттер және оларға сәйкес келетін
интервалдар жаңаша консонанс деп аталды және келесі есімдерге ие болды:
октава (w2w1=21, l2l1=12);
квинта (w2w1=32, l2l1=23);
кварта (w2w1=43, l2l1=34).
Музыкалық гаммадағы дыбыстар белгілі тәуелділікпен бір-бірімен
байланысты. Біреулері тұрақсыз болып, тұрақтыларға қарай жақындай береді.
Әр гаммада неғұрлым тұрақты негізгі тон бар. Ол тоника деп аталады, және
одан берілген музыкалық жүйе басталады. Лад – белгілі дыбыс шығару сипаты
бар және тұрақты дыбыстардан тұрақсыз дыбыстардың тәуелсіздігін анықтайтын
музыкалық дыбыстардың құлаққа жағымды өзара қарым-қатынасы. Ладтың дыбыстық
көтерілу қатынасы жүйесінің математикалық өрнегі – музыкалық қатар деп
аталады.
Пифагоршылар музыкалық шкала – гаммасы негізін октава интервалы деп
санады. Ол жоғарғы дыбысты қайталайтын консонанс. Музыкалық гамманы құру
үшін пифагоршыларға октаваны әдемі дыбыс шығаратын бөліктерге бөлу қажет
болды. Өйткені, пропорцияның кереметтілігіне сенді. Олар гамманың
құрылғысын орта шамамен байланыстырды: арифметикалық, геометриялық,
гармониялық:
орташа гармониялық орташа геометриялық
------------------------= --------------------------------
-------
орташа геометриялық орташа арифметикалық

орташа арифметикалық = (А+В)2
орташа геометриялық = sqrt(АВ)

орташа гармониялық sqrt(АВ)
-----------------------------= ------------------------
-- ---
sqrt(АВ) (А+В)2

sqrt(АВ) ( sqrt(АВ) 2АВ
орташа гармониялық = -------------------= --------------
---- --
(А+В)2 (А+В)

Тоника және октаваны қайталау үшін орта арифметиканы құрамыз. Өйткені:
w2=2w1, онда w3=(w1+w2)2=3w12 немесе w3w1=32.
Толқынды қозғалысты w1 және w2 жиіліктерінің орта арифметикасы тағы да
бір керемет консонанс – квинтаны табуға көмектеседі. Шектің l3 ұзындығы
Пифагор – Архиттің екінші заңы бойынша l1 және l2=12l1 шектерінің
ұзындығының орта гармониясы болады;
l3=2l1*l2(l1+l2)=l3l1=23.
Әрі қарай негізгі тонның w1 және w2 жиілігінің орта гармониясын алып:
w4=2w1*w2(w1+w2)=4w13=w4w1=43 екенін аламыз.
Соның нәтижесінде тағы да бір керемет консонанс - квартаны табамыз.
Табылған жиіліктегі шектердің ұзындығы қалай байланыста екенін анықтаймыз.
Түрлендіруді біртіндеп орындаймыз:
w4=2w1*w2(w1+w2) мұндағы w=al, одан l4=(l1+l2)2=34l1; l4l1=34
екенін аламыз.
Демек, l1, l3 және l4 шектерінің ұзындығы бір-бірімен орта
арифметикамен байланысты.
Яғни, квинта негізгі тонның және октаваның жиілігінің орта арифметикасы
болады, ал кварта – орта гармониясы болады.
Бұл тек тамаша пропорцияның пифагорлық музыкада орындалған шамалы
бөлігі ғана. Пифагоршылар дыбыстардың гармониясы деп қоршаған ортаның
әдемілігі, яғни терең гармонияның пайда болуы деп санады.
Жоғарыда сипатталғаннан басқа музыкалық гамманың құрылымының басқа
тәсілі бар болады. Ол өте оңай және ыңғайлы болады. Және әлі күнге шейін
музыкалық аспаптардың құлақ күйін келтіруде қолданылады.
Гамманы керемет консонанстар - квинта мен октаваны қолдана отырып
құруға болады екен. Бұл тәсілдің мәні шыққан дыбыстың, мысалға до
(32)0=1, біз квинта бойынша жоғарға немесе төменге жылжимыз және алынған
дыбыстарды бір октаваға жинаймыз. Сонда:
(32)1 =32 – соль,
(32)2 2 =98 – ре,
(32)3 2 =2716 – ля,
(32)4 4 =8164 – ми,
(32)5 4 =243128 – си,
(32)–1 2 =43 – фа
екенін аламыз.
Музыкалық гамманың соңғы құрылымының мынадай ерекшелігі бар: квинталар
бойынша жоғарғы және төмен жылжығанда берілген дыбыстың нақты қайталануы
болмайды. Тек 12 квинта 7 октава жуық шамамен тең. Ал оларды бөліп тұрған
интервал пифагорлық комма деп аталады. Өзінің кішілігіне қарамастан кома
көптеген жылдар бойы музыканың құлағын шулатты. (32)12128 қатынасын ала
отырып, пифагорлық комманың (1, 0136) сандық мәнін табуға болады.
Сонымен, дыбыстардың гармониясында пифагоршылар космос гармониясын
жүзеге асырды. Қоршаған ортанының жаңа идеясы келесі эпохаларда ғалымдардың
ойлауынан шыққан жоқ.
ХІХ ғасырдың екінші жартысында Кеплер 7 негізгі гармониялық интервал
белгіледі:
21 – октава,
53 – үлкен секста,
85 – кіші секста,
32 – таза квинта,
43 – таза кварта,
54 – үлкен терция,
65 – кіші терция.
Осы интервалдардың көмегімен ол барлық дыбыстық қатарды мажорлық және
минорлық бағытталуын шығарды. Аспандағы гармониялық қатынастарды ұзақ
іздеу нәтижесінде үлкен есептеу жұмыстарын жүргізе отырып, Кеплер
экстремальдық жылдамдықтар бұрышының қатынасы гармониялық қатынастарға
кейбір планеталар үшін жақын екенін анықтады:
32 – Марс, 65 – Юпитер, 54 – Сатурн.
Әрі қарай ол Сатуран және Юпитер баспен ән салады, Марс – тенормен,
Жер және Шолпан – альтпен, ал Меркурий – дискантпен. Ғалым ешқандай дәлел
келтірмейді.
XVIII ғасырда музыка тарихының жаңа беттерін ашты. 1700 жылдарда неміс
органаисті А. Веркмайстер керемет шешімді жүзеге асырды: пифагорлық
гамманың консонанстарына қарсы болды ... Октаваны сақтап, оны екі тең
бөлікке бөлді.
Жаңа музыкалық қатар әуенге мүмкіндік берді. Осы қатардың енгізілуіне
байланысты музыкада темперация үстем болды (латын тілінен – мөлшерлестік).
Бірқалыпты қатардың математикалық түсіндірмесі қандай екен?
Гамманы құру үшін оны әдемі дыбысталатын бөліктерге бөлу қажет. Яғни,
оның белгілі сандар негізінде толық анықтайтын w жиілілік және 2w арасында
кейбір шкаланы енгізу керек болды (соншалықты октаваға бөлінеді).
Гаммаларды құруда көбінесе жиілікке сәйкес келетін мына логарифмдерді
қолданған ыңғайлы екен: log2w0, log2w1... log2wm. Октава log2w0-ден log2 2w0
= log2w0 (1- ге дейін аралықта ауысады, яғни 1 ұзындығы аралығында.
Октаваны тең бөліктерге бөлу үшін халықтық музыкасының көптеген
дәстүрлі мысалдарының талдауы қажет. Көбінесе онда жиілікке қатысты
көмегімен өрнектелетін интервал жиі кездеседі:
21 – октава,
32 – квинта,
54 – терция,
43 – кварта,
53 – секста,
98 – секунда,
158 – септима.
Бұл және басқа нәтижелер музыкалық шкала 12 бөлікке бөлінуі керек
екенін көрсетті. Веркмайстер келтірген органы тепе-тең шапшаңдық қарқынымен
ойнады. Жаңа қатардың басымырақ екені даусыз. Қатар музыкалық естуде
әуендік, сонымен қоса гармониялық қатынас сияқты тұйық түр көрсетіп,
интервалдардан тұрды. Онда үндестілік бір үндестілікке ауысуды жайбрақат
байқауға болады. И. С. Бах 12 мажорлық және 12 минорлық шығармадан тұратын
Жаңа шапшаңдық қарқын клавирін жазып, жаңа музыкалық жүйенің бар
екендігін дәлелдеді. [2]

ІІ Тарау. Терминология.

1 бөлім. Тізбектер және параллельдер

Математикада тізбектер түсінігімен біз өте жиі кездесеміз. Әдетте,
олармен кездесу мақсаты – келесі санды немесе символды табу (математикадағы
тізбектер - символдардың реттелген қатары). Бұның мәні - берілген тізбек
бағынатын заңдылықты табу. Мысалы:
991, 19, 10, 1, 1, 1...
1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
Санды тізбектерден санды пирамиданы құруға болады:
1(8 + 1 = 9
12(8 + 2 = 98
123(8 + 3 = 987
1234(8 + 4 = 9876
12345(8 + 5 = 98765
123456(8 + 6 = 987654
1234567(8 + 7 = 9876543
12345678(8 + 8 = 98765432
123456789(8 + 9 = 987654321

1(11 = 11
11(111 = 1221
111(1111 = 123321
1111(11111 = 12344321
Математикадығы ерекше тізбектер - арифметикалық және геометриялық
прогрессия, (дегенмен, прогрессия түсінігімен өмірде де жиі кездесуге
болады).
Арифметикалық прогрессия –
екіншісінен бастап әрбір мүшесі өзінің алдындағы мүшеге бірдей санды
қосқанға тең болатын санды тізбек.
Геометриялық прогрессия –
екіншісінен бастап әрбір мүшесі өзінің алдындағы көршілес мүшені бірдей
санға көбейткенде шыққан нөлден өзгеше болатын санды тізбек
Бұл екі прогрессияның музыкада орын алуы да ғажап емес.
Ұзақтықтың құрылу принципі геометриялық прогрессияның құрылу принципіне
сәйкес келеді. Егер ұзақтықты дәрежесі бойынша кемуімен бүтіннен
(музыкада бірлік болатын) жазсақ, онда мынаны аламыз:

Математикада мұндай тізбекті кемімелі шектеусіз геометриялық прогрессия
деп атайды. Бөлгіш модулі бірліктен кіші болатын шектеусіз геометриялық
прогрессия (осы жағдайда - )

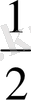Алайда, арифметикалық прогрессия да аталды. Осыған байланысты музыкалық
түсінік квинталық өріске тоқталмау мүмкін емес.
Квинталық шеңбер кез келген үндестілік болып көрінеді. (Қандай да бір
үндестілікте музыканы жазу үшін, оның тоникасын және белгі таңбасын білу
керек. Квинталық өріс берілген шартты нақтылайды).
Оның құрылу принципі өте қарапайым: квинтадағы үндестілік тониканың
артуымен үндестіліктегі таңба саны бірлікке артады (шынында, мұнда біз екі
арифметикалық прогрессиямен кездесеміз).
Алайда, егер үндестіліктегі белілердің шығу принципін саны емес, сапасы
жағынан талдап шықсақ, онда келесіні байқаймыз:
- диездер үшін (диез – бұл жартытондағы дыбыстың көтерілуі):
Фа До Соль Ре Ля Ми Си
- бемольдар үшін (бемоль – бұл жартытондағы дыбыстың төмен түсуі):
Си Ми Ля Ре Соль До Фа.
(біреуі басқасын керісінше дейінгі дәлдікпен қайталауы қызықты).
Арифметикалық прогрессияны қолдану әдісі классикалық музыкадағы сияқты,
қазіргі музыкада да кең таралған. Прогрессияның айырмасына сүйеніп –
квинта – аккордтардың тізбегін жасауға болады, мұндағы әрбір алдыңғы аккорд
доминанта болып шығады (доминанта – бесінші сатыда құрылған үндестіліктегі
үн, квинта бес деп аударылады). Мұндай тізбек бұрын көрсетілгендей
үндестіліктегі тұрақты және тұрақты емес саты болу салдарынан естуде
жағымды. Тұрақтыға жақындайтын тұрақты емес дыбыстар аяғында тұрақтыға
ауысады (немесе, музыкалық теоретиктер айтқандай рұқсат етіледі). Доминанта-
тониканы ең атақты деп санауға болады. Ең болмағанда, әлемдегі бар және
бар болатын, шамамен 99%-і, әуендер осылай аяқталады.
Жазылған прогрессия И. С. Бах, В. А. Моцарт, Л. В. Бетховеннің
музыкасында да қабылданған. Бұдан композиторлардың кереметтілін жаңа шегін
көруге болады. Мұндай прогрессия қазіргі орыс және шетел музыкаларында
кездеседі (іс жүзінде барлық стильде), кереметтілік туралы ойға
итермелемейді, қазіргі күнгі ең танымал 25-тен аса әуенді талдап шығып,
квинтадағы айырмассымен прогрессияны ғана емес, сонымен бірге кіші
секундты, үлкен секунданы, кіші терцияны, үлкен терцияны және де бір-
бірінен көшірілген аккордттар тізбегін көруге болады.
Аккордтардан басқа, негізінен аккомпанементте қолданылатын (әуенді
сүйемелдеу ) әуеннің өзін арифметикалық прогрессия көмегімен модельдеуге
болады. Бұл бірінші кезекте секвенцияға қатысты.
Секвенция – бұл музыкалық әдіс, мұнда әртүрлі дыбыстардан тұратын бір
және сол әуен бірнеше рет қайталанады, (музыкада оны музыкалық фраза деп
айтуға қабылданған). Сонымен бірге, бұл дыбыстар арифметикалық прогрессияны
бейнелейді.
Алайда әр түрлі дыбыстардан тұратын бір және сол әуенді қайталауды бір
дыбыстан басқа дыбысқа параллель көшірумен салыстыруға болады, алайда
параллель сөзі қасында жүр дегенді білдіреді. Егер екі бірдей әртүрлі
дыбыстардан тұратын әуенді бір мезгілде ойнаса, шынымен онда қиылыспайды.
Параллельдік тақырыбын жалғастырып, сонымен бірге бұл ұғымсыз
музыкадағы трансляциялау туралы айтпауға болмайтынын ескертуге болады.
Музыкадағы трансляция – сол және басқа үндестілікті қолдану ыңғайсыздығынан
композиторлармен орындаушылар жиі қолданатын бір үндестіліктен келесі
үндестілікке көшу. Ыңғайсыздықтың себебі әр түрлі болуы мүмкін.
Орындаушылар үшін (яғни олардың дауысы үшін) бұл көбінесе тым биік және тым
аласа регистр, ал композиторлар үндестілікті іздеуден түпкі ойды табады.
Тіпті математика көзқарасынан барлық мажорлардың және барлық минорлардың
құрылуы тепе-тең, ал дыбысталуында басқаша. Әрбір үндестілік өзінің
қайталанбас музыкалық өзгешелігіне ие болады. Әуенді трансляциялау
көмегімен бұл өзгешелікті композиторлар табуға ұмтылады.
Параллельдік әдісті көпдауысты музыкада да кең қолданады. Екі және
одан артық дауыстарды параллель партия бойынша өте жиі орындайды, яғни
бірдей қиылыспайтын әртүрлі дыбыстардан басталатын әуендер. Композиторларда
сүйікті айырмалар - терция, секста және октава. Берілген
айырмашылықты қолдану әр түрлі мақсатты көздеуі мүмкін. Мысалы, көпдаусты
музыкадағы октава салтанатты немесе, керісінше, өте қатты, тұңжыраңқы
музыкада дыбысталады. Терция лирикалық музыкада (әдетте, дуэтта), ал секста
– терцияда және квартетада қолданылады.
Мұндай музыкалық канон сияқты түр параллельдіктің арқасында шықты деп
айтуға болады. Канон заңды білдіреді және музыкалық түрге жатады. Мұнда
кейбір әуендер бір немесе сол дыбыстан бірнеше рет кейбір интервалдармен
қайталанады. Канондар көпдаустарда, яғни орындаушылар халықтық музыкада,
шіркеулік музыкада, операда және опереттада машықтануы үшін қолданады.
Музыкадағы параллельдік туралы сөзді аяқтай отырып, параллель сөзі
параллель үндестілік түсінігінде кездесетінін айту керек (мұндай үндестілік
те әртүрлі тоника болады, бірақ белгідегі бірдей таңбалар, яғни егер оларды
бір мезгілде ойнаса, онда олар қиылыспайды). [3]

2 Бөлім. Ритмдер.

Ырғақ сөзі басынан музыкаға тән, тіпті басқа деректерден адамға белгілі
екені таңданарлықтай емес. Ожегованың сөздігінде ырғақ кейбір
элементтердің бірқалыпты кездесуі сияқты анықталады. Музыкалық ырғақ
анықтама емес, мысал ретінде беріледі. Сөйтіп, ырғақты ғылым және өнер
аясында интернациональды деп айтады.

Математикалық заңдылықтарды және санды тізбектерді зерттеп, ырғақтықты
жиі байқауға болады. Дербес жағдайда, математикалық ырғақтың қарапайым
мысалдары периодтық бөлшектер болады (сонымен қатар, период сөзі
музыканттарға да таныс)

Бірнеше қызықты мысалдарды қарастырайық:

17 = 0, 142857...
27 = 0, 285714...
37 = 0, 428571...
47 = 0, 571428...
57 = 0, 714285...
67 = 0, 857142...

Берілген бөлшектер (әсіресе, олардың периодтары) тек өзіне ғана емес,
сонымен бірге салыстыруына да көңіл аудартады.

Тағы бір топты қарастырайық:

19 = 0, 11...
199 = 0, 0101...
1999 = 0, 001001...
19999 = 0, 00010001...

келесімен салыстырып:

11111 = 0, 00090009...
1111 = 0, 009009...
111 = 0, 0909...
1 = 0, 99...

Мынадай бөлшектер көңіл бөлуді қалайды:

127 = 0, 037037...
137 = 0, 027027...

Сонымен, біз периодты бөлшектердің ырғақтылығын басқа бөлшектерді
салыстыру және салыстырмау сияқты көздейміз.

Енді санды кестеде жасырылған ырғақтарды табуды іздестіреміз. Музыкада
белгілі болатындай ырғақ дұрыс және дұрыс емес болады.

Пифагор квадратын қарастырайық:

1 2 3 4
до w 9w8 ре
ре 9w8 81w54 ми
ми 81w64 729w512 ?
фа 4w3 3w2 соль
соль 3w2 27w16 ля
ля 27w16 243w128 си
си 243w128 2187w1024 ??

Дегенмен 43 729512 32 болғанымен ? белгісі көрсетілген клеткада
фа-дан жоғары, бірақ соль-дан төмен дауыс орналасуға тиісті. Тиісті нотаны
фа-диез деп атады. Сондай клеткада белгіленген ?? келесі октавадағы додан
жоғары, бірақ ре-ден төмен дауыс орналасуға тиісті. Мұндайда 2w жиіліктегі
до арасындағы интервал мен сол дауыстағы фа және фа-диез арасындағы
интервал да осындай. Яғни осы дауысқа тиесілі нотаны ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.