Идеал газ молекулаларының Максвелл жылдамдық пен энергия үлестірілімдері, Больцман таралуы және еркін қозғалыс ұзындығы


Статистикалық үлестірілулер
Идеал газ молекулаларының жылдамдық бойынша және жылулық қозғалыстың энергиясы бойынша таралуының Максвелл заңы. Молекулалық-кинетикалық теорияның негізгі заңын қорытқан кезде молекулалар әртүрлі жылдамдықпен қозғалады дедік. Көптеген соқтығысулар нәтижесінде әр молекуланың жылдамдығы модулі және бағыты бойынша өзгереді. Бірақ молекулалардың хаосты қозғалуының нәтижесінде барлық қозғалыс бағыттары ықтимал, яғни орташа есеппен кез-келген бағытта қозғалатын молекулалар саны бірдей.
Молекулалық-кинетикалық теория бойынша молекулалар соқтығысқанда жылдамдық қанша өзгергенімен газдағы массасы
m
0
молекуланың тепе-теңдік қалыпта тұрақты температурадағы Т=
const
орташа квадраттық жылдамдығы
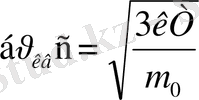 тең. Мұны былай түсіндіруге болады: Т=
const
болғанда тепе-теңдік күйдегі газда уақыт уақыт бойынша өзгермейтін молекулалардың жылдамдық бойынша таралуы, яғни стационар таралуы орын алады. Ол белгілі бір статистикалық заңға бағынады, теория жүзінде ол заңды қорытып шығарған Дж. Максвелл.
тең. Мұны былай түсіндіруге болады: Т=
const
болғанда тепе-теңдік күйдегі газда уақыт уақыт бойынша өзгермейтін молекулалардың жылдамдық бойынша таралуы, яғни стационар таралуы орын алады. Ол белгілі бір статистикалық заңға бағынады, теория жүзінде ол заңды қорытып шығарған Дж. Максвелл.
Молекулалардың жылдамдық бойынша таралу заңын қорытып шығарғанда Максвелл газ өте көп молекулалардан тұрады, молекулалар бірдей температурада тәртіпсіз жылулық қозғалыста болады және газға күш өрістері әсер етпейді деп алды.
Максвелл заңы
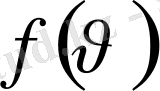 функциясымен сипатталады, ол функция молекулалардың жылдамдық бойынша таралу функциясы деп аталады.
функциясымен сипатталады, ол функция молекулалардың жылдамдық бойынша таралу функциясы деп аталады.
Егер молекулалардың жылдамдық диапазонын
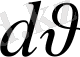 -ға тең кіші интервалдарға бөлсек, онда жылдамдықтың әрбір интервалына
-ға тең кіші интервалдарға бөлсек, онда жылдамдықтың әрбір интервалына
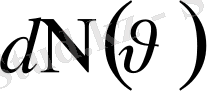 молекулалар саны келеді,
молекулалар саны келеді,
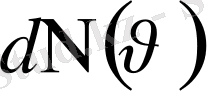 молекулалардың жылдамдығы осы интервалда жатады.
молекулалардың жылдамдығы осы интервалда жатады.
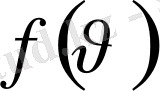 функциясы жылдамдықтары
функциясы жылдамдықтары
 дан
дан
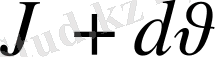 интервалында жатқан молекулалардың салыстырмалы санын анықтайды:
интервалында жатқан молекулалардың салыстырмалы санын анықтайды:
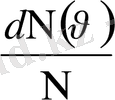 , яғни
, яғни
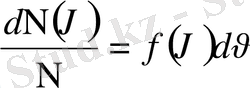 бұдан
бұдан
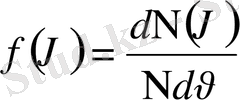 .
.
Ықтималдылық теориясының әдістерін пайдалана отырып, Максвелл
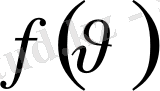 функциясын - идеал газ молекулаларының жылдамдық бойынша таралу заңын тапты:
функциясын - идеал газ молекулаларының жылдамдық бойынша таралу заңын тапты:
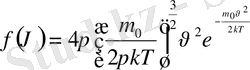 (1)
(1)
Формуладан көргендей
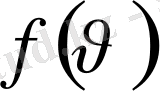 функциясы газдың массасына және температураға Т тәуелді.
функциясы газдың массасына және температураға Т тәуелді.
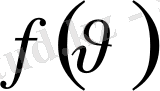 функциясының графигі 6 суретте көрсетілген.
функциясының графигі 6 суретте көрсетілген.
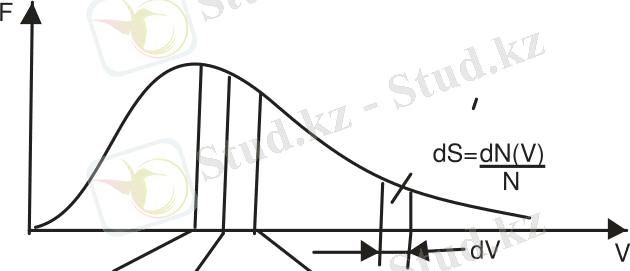
Сурет 6
Егер
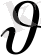 өскен сайын
өскен сайын
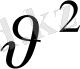 -на қарағанда
-на қарағанда
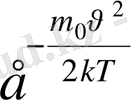 тез азайса, онда
тез азайса, онда
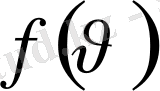 функциясы нульден бастап
функциясы нульден бастап
 тең болғанша өседі,
тең болғанша өседі,
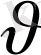 =
=
 болғанда максимумға жетеді, сосын асимптотикалы нульге ұмтылады. Қисық
болғанда максимумға жетеді, сосын асимптотикалы нульге ұмтылады. Қисық
 -ға қарағанда симметриялы емес.
-ға қарағанда симметриялы емес.
Жылдамдығы
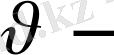 дан
дан
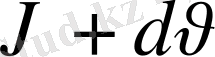 интервалында жатқан молекулалардың салыстырмалы саны
интервалында жатқан молекулалардың салыстырмалы саны
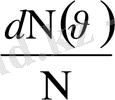 - ақшыл жолақтың ауданы болып табылады. Таралу қисығымен және абсцисса осімен шектелетін аудан бірге тең, ол
- ақшыл жолақтың ауданы болып табылады. Таралу қисығымен және абсцисса осімен шектелетін аудан бірге тең, ол
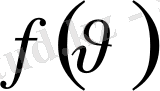 функциясы нормалау шартын қанағаттандырады дегенді білдіреді:
функциясы нормалау шартын қанағаттандырады дегенді білдіреді:
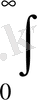
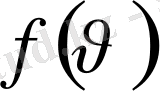
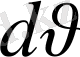 =
1
=
1
Идеал газдың жылдамдық бойынша таралу функциясы максимал мәнге ие болатын жылдамдықты ықтимал жылдамдық деп атайды. Ықтимал жылдамдықтың мәнін (1) формуланы жылдамдық бойынша дифференциалдап және нульге теңеп,
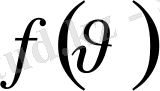 өрнегі үшін максимум шартын қолдана отырып табуға болады:
өрнегі үшін максимум шартын қолдана отырып табуға болады:
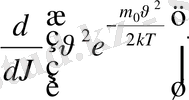 =
2
=
2
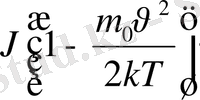
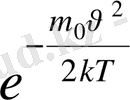 =
0
=
0
 =
0 және
=
0 және
 =
=
 өрнегінің минимум шартына сәйкес келеді, жақша ішіндегі өрнек нульге тең болатын болса, ықтимал жылдамдықтың
өрнегінің минимум шартына сәйкес келеді, жақша ішіндегі өрнек нульге тең болатын болса, ықтимал жылдамдықтың
 мәнін табуға болады:
мәнін табуға болады:
 =
=
 =
=

Егер температура жоғары болса, максимум оңға жылжиды,
 мәні үлкен болады. Бірақ қисықпен шектелген аудан өзгермейді, тек температура өскенде қисық созылады және аласарады (сурет 7 ) .
мәні үлкен болады. Бірақ қисықпен шектелген аудан өзгермейді, тек температура өскенде қисық созылады және аласарады (сурет 7 ) .
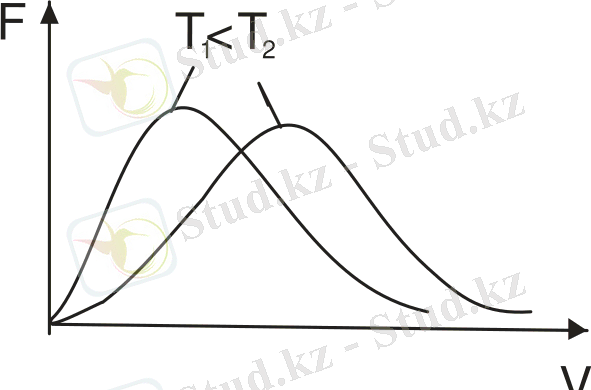
Сурет 7
Таралу функциясы арқылы молекулалардың орташа арифметикалық жылдамдығын мына формуладан табады:
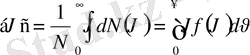
 функциясының мәнін қойып және интегралдап, орташа арифметикалық жылдамдықтың өрнегін алады:
функциясының мәнін қойып және интегралдап, орташа арифметикалық жылдамдықтың өрнегін алады:
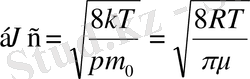
Газ күйін сипаттайтын жылдамдықтар:
1) ықтимал жылдамдық -
 =
=
 ;
;
2) орташа арифметикалық жылдамдық -
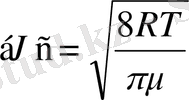 ,
,
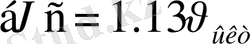 ;
;
3) орташа квадраттық жылдамдық -
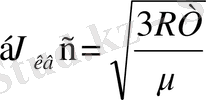 ,
,
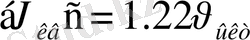 .
.
Молекулалардың жылдамдық бойынша үлестірілуінен газ молекулаларының кинетикалық энергия бойынша үлестірілуі функциясын алуға болады.
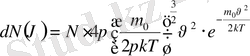
Ол үшін жоғарыдағы өрнектегі айнымалы жылдамдық
 шамасынан кинетикалық энергия
шамасынан кинетикалық энергия
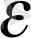 шамасына көшу қажет:
шамасына көшу қажет:
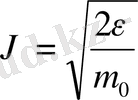 ,
,
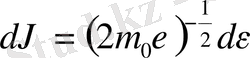 . Сонда өрнекті мына түрде жазуға болады:
. Сонда өрнекті мына түрде жазуға болады:
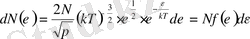 ;
;
Мұндағы
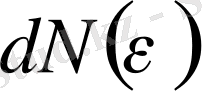 -
-
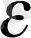
 интервалындағы ілгерілемелі қозғалыстың кинетикалық энергиясы бар молекулалар саны. Сонымен, молекулалардың жылулық қозғалысының энергиясы бойынша таралу функциясының өрнегін жазайық:
интервалындағы ілгерілемелі қозғалыстың кинетикалық энергиясы бар молекулалар саны. Сонымен, молекулалардың жылулық қозғалысының энергиясы бойынша таралу функциясының өрнегін жазайық:
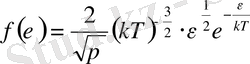 (2)
(2)
Идеал газдың орташа кинетикалық энергиясын таралу функциясын пайдаланып табуға болады:
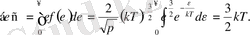
Барометрлік формула. Больцман таралуы. Молекулалық-кинетикалық теорияның негізгі теңдеуі бойынша және Максвелл таралу заңы бойынша газ молекулаларына сыртқы күштер әсер етпейді, сондықтан олар көлемде бірқалыпты таралады деп есептелінді. Бірақ кез-келген газдың молекуласы Жердің тартуының потенциалдық өрісі әсерінде болады. Ауырлық күші мен молекулалардың жылулық қозғалысы газдың стационар күйіне әкеледі, газ қысымы биіктікке байланысты азаяды. Тартылыс өрісін біртекті, температура тұрақты және барлық молекулалардың массасы бірдей деп алып, қысымның биіктікке байланысты өзгерісін көрсететін заңды қорытайық (сурет 8) . Егер h биіктікте атмосфералық қысым p -ға тең болса, онда h + dh биіктікте ол p+dp -ға тең ( dh >0 болғанда dp <0, себебі қысым биіктікпен азаяды) .
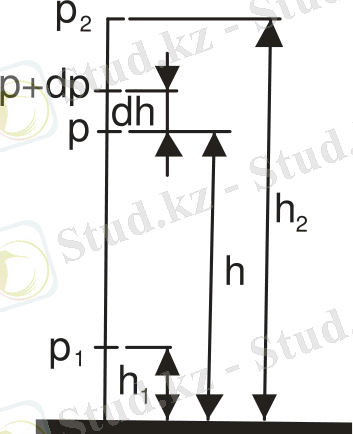
Сурет 8
Қысымның биіктікке байланысты өзгерісін көрсететін заңды қорытқанда, өріс біртекті, температура тұрақты және барлық молекулалардың массасы бірдей деп аламыз. Егер h биіктікте атмосфералық қысым р -ға тең болса, онда h+dh биіктікте ол p+dр -ға тең (dh>0 болғанда dр>0 , себебі қысым биіктікпен азаяды) p және р+ dр қысымының айырмасы биіктігі dh -қа тең цилиндрдің көлемінің ішіндегі газдың салмағына тең p-(p+dp) = ρgdh, ρ- газдың тығыздығы, dh- өте аз биіктік болғандықтан газдың тығыздығын өзгермейді, тұрақты деп алуға болады. Сондықтан
dр = - ρgdh
Идеал газдың күй теңдеуін пайдалана отырып,
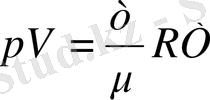 ,
тығыздықты табамыз
,
тығыздықты табамыз
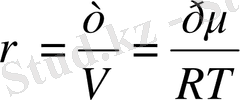
Оны формулаға қойып, мынаны аламыз
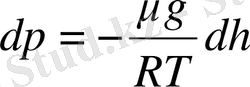 ,
,
немесе
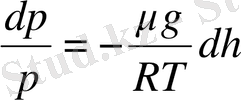
Биіктік h 1 -ден h 2 -ге өзгергенде қысымда р 1 - ге ден р 2 - ге өзгереді, яғни
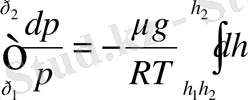
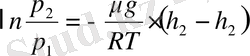 ,
,
немесе
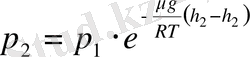
Алынған формула барометрлік формула деп аталады, ол биіктікке байланысты атмосфералық қысымды табуға немесе қысымды өлшеп алып, сол арқылы биіктікті табуға мүмкіндік береді. Биіктік теңіз деңгейіне қатысты өзгереді:

деп жазуға болады, мұндағы р - h биіктіктегі қысым. Биіктікті өлшейтін құралды альтиметр деп атайды. Бұл формула газ ауыр болған сайын оның қысымы биіктікке байланысты тез кемитінін көрсетеді. Барометрлік формуланы р=nkТ өрнегін пайдаланып былай жазуға да болады:
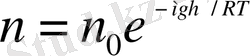
п - h биіктіктегі молекулалардың концентрациясы, n 0 - h=0 биіктіктегі молекулалардың концентрациясы.
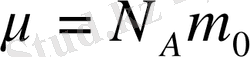 және
және
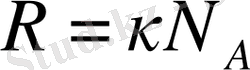 болғандықтан
болғандықтан
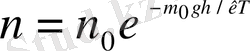 потенциалдық энергиясы екенін ескеріп, бұл өрнекті мына түрде жазуға болады:
потенциалдық энергиясы екенін ескеріп, бұл өрнекті мына түрде жазуға болады:
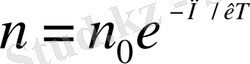
формуласы сыртқы потенциалдық өрістегі Больцман таралуы деп аталады. Тұрақты температурада Т=const молекуланың потенциалдық энергиясының кемуіне сол жердегі газ тығыздығының көбеюі сәйкес келеді. Жылулық хаосты қозғалыстағы молекулалардың массалары бірдей болса, Больцман таралуы тек қана ауырлық күші өрісінде емес, сыртқы потенциалдық өрісте де орынды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz