Электростатика: Кулон заңы, электр өрісінің қасиеттері, потенциал және сыйымдылық


ЭЛЕКТР ЖӘНЕ МАГНЕТИЗМ
Тақырып: Электростатика.
Электростатикалық өрістің қасиеттері
Ағылшын физигі Ш. Кулон күйектелі таразының көмегімен вакуумдегі бір-бірінен арақашықтықта тұрған нүктелік екі зарядтардың өзара әсерлесу күшін тәжірибе жасап анықтаған. Кулон заңы: Вакуумдегі (бостықтағы) нүктелік екі зарядтардың өзара әсерлесу күші, сол зарядтардың көбейтіндісіне тура пропорционалды, арақашықтықтарының квадратына кері пропорционал болады.
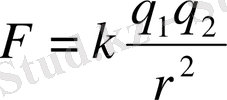 (1. 1)
(1. 1)
Әскрлесу күші зарядтарды қосатын түзудің бойымен болады, сондықтан Кулон күшін
центрлік күш
дейді. Зарядтардың таңбалары қарама-қарсы болса, онда олардың арасында тарту күші әсер етеді.
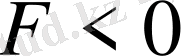 , ал зарядтардың таңбалары бірдей болса, онда ондай зарядтар бірін-бірі тебеді
, ал зарядтардың таңбалары бірдей болса, онда ондай зарядтар бірін-бірі тебеді
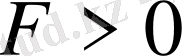 болады. (1. 1) формуласын векторлық күйде былай жазамыз.
болады. (1. 1) формуласын векторлық күйде былай жазамыз.
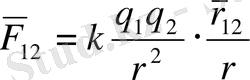 (1. 2)
(1. 2)
ХЖ жүйесінде пропорционалды коэффициент
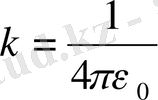 болады. Сонда ХЖ жүйесінде Кулон заңы былай жазылады.
болады. Сонда ХЖ жүйесінде Кулон заңы былай жазылады.
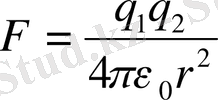 (1. 3)
(1. 3)
Мұндағы
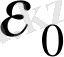 - электрлік тұрақты
- электрлік тұрақты
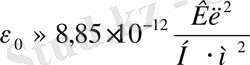 ; немесе
; немесе
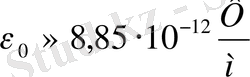 ;
;
2. Зарядталған бөлшектердің өзара әсерлесуі олардың айналасындағы электр өрісі арқылы болады. Кез-келген зарядталған дененің (бөлшектің) айналасында электр өрісі болады. Қозғалмайтын зарядтың айналасындағы өрісі электростатикалық өріс деп атайды. Электр өрісі материяның ерекше бір түрі. Кез-келген жерде электр өрісінің бар, жоғын сол нүктеге қойылған сыншы заряд арқылы анықтаймыз. Өріс сыншы зарядқа белгілі бір күшпен әсер етеді. Сыншы зарядтың шамасы, сол нүктедегі өрісітің шамасын өзгерте алмайтындай өте кішкентай болу керек.
Электростатикалық өрістің күйін анықтайтын негізгі парасетрдің (шаманың) бірі - өрістің кернеулігі. Өрістің кернеулігі, оның сол нүктедегі күштік сипаттамасын өрнектейді. Енді, сол өрістің керенулігін анықтайық.
 -зарядының одан
-зарядының одан
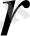 арақашықтықтағы нүктесіндегі өрісінің кернеулігін анықтайық.
арақашықтықтағы нүктесіндегі өрісінің кернеулігін анықтайық.
Ол сол нүктеге
 ′,
′,
 ″,
″,
 ′″ сыншы зарядтарына кезекпе кезек қойып, әр сыншы заряд үшін Кулон күшін жазайық.
′″ сыншы зарядтарына кезекпе кезек қойып, әр сыншы заряд үшін Кулон күшін жазайық.
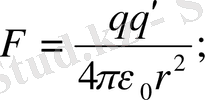
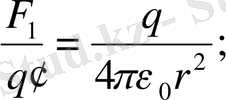
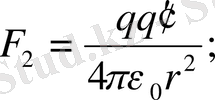
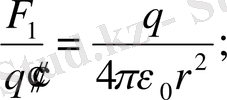
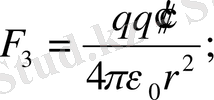
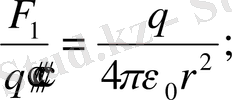
Сонда
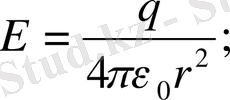
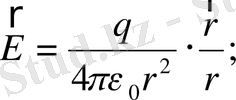
 - электр өрісінің алынған нүктесіндегі кернеулігі, кернеулік векторлық
- электр өрісінің алынған нүктесіндегі кернеулігі, кернеулік векторлық
шама.
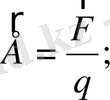
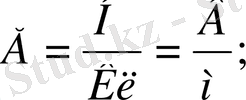
Өрісті көрнекті ету үшін Фарадей күш сызықтары деген ұғым енгізген. Күш сызықтарының әр-бір нүктесіне жүргізілген жанама, сол нүктедегі өрістің кернеулігінің бағыты мен шамасын көрсетеді.
Өрістің күш сызықтарының жолына перпендикуляр қойылған бір өлшем ауданнан өтетін күш сызықтарының санын, күш сызықтарының тығыздығы дейді. Ол модуль жағынан сол жердегі өрістің кернеулігінің шамасына тең болады.
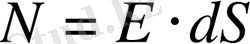 (1. 4)
(1. 4)
мұндағы N, dS ауданды қиып өтетін күш сызықтарының саны.
Егер өрістің кернеулік күш сызықтары
dS
ауданына тұрғызылған (
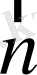 ) нормаль мен
) нормаль мен
 бұрышын жасайтын болса онда
бұрышын жасайтын болса онда
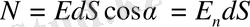 (1. 5)
(1. 5)
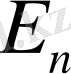 - өрістің нормальға түсірілген проекциясы.
- өрістің нормальға түсірілген проекциясы.
dS - ауданды қиып өтетін барлық күш сызықтарының санын, сол аудан арқылы өтетін кернеулік векторының ағыны дейді.
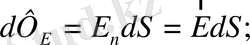 (1. 6)
(1. 6)
Кернеулік ағынының өлшем бірлігі В . м .
Жалпы алғанда кез-келген тұйық контурды қиып өтетін кернеулік векторының ағынын былай анықтаймыз:
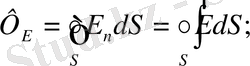 (1. 7)
(1. 7)
Әр уақытта есте болатын жағдай : оң зарядтың кернеулігінің күш сызықтары зарядтан шығып жатады, ал теріс зарядтың кернеулігінің күш сызықтары зарядқа еніп жатады.
Электростатикалық өрістің суперпозициялық принципі. Диполь
Бірнеше
q
1
, q
2
, q
3
……q
n
зарядтардың бір сынақшы
q
0
заряд тұрған нүктесіндегі өрістің кернеулігі, сол нүктедегі әрбір зарядтың кернеулігінің геометриялық қосындысына тең.
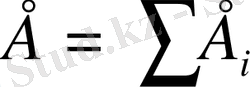 осыны өрістің суперпозициялық принципі дейді.
осыны өрістің суперпозициялық принципі дейді.
Басқаша айтқанда кеңістіктің бір нүктесінде бірнеше өріс кездессе, олардың бір- бірімен беттесуін (қосылуын) айтамыз. Бұл принцип барлық өрістерге тән қасиет.
Шамалары жағынан тең, таңбалары қарама-қарсы екі заряд системасын электрлік диполь дейді.
 - дипольдің өсі.
- дипольдің өсі.
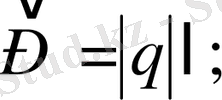
диполь моменті. Мұндағы
 - дипольдің иіні делінеді.
- дипольдің иіні делінеді.
Өрістің суперпозициялық принципі бойынша дипольдің айналасындағы кез-келген нүктедегі дипольдің өрісінің кернеулігі
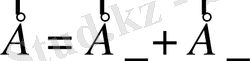 оның оң және теріс зарядтарының сол нүктедегі кернеуліктерінің қосындысына тең.
оның оң және теріс зарядтарының сол нүктедегі кернеуліктерінің қосындысына тең.
Гаусс теоремасы. Радиусы r сфера беттің центрінде q заряд болсын. Ол зарядтың өрісінің кернеулігінің күш сызықтарын сфера бетті қияп жатады. Сонда сфера бетті қиып өтетін кернеулік векторының ағыны
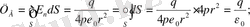
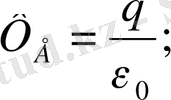 (1. 8)
(1. 8)
(1. 8) кез-келген формадағы тұйық бет үшін әруақытта орындалады. Егер біз n зарядты қамтитын кез-келген формалы тұйық бет алсақ, суперпозицияпринципі бойынша қорытқы өрістің кернеулігі, ал зарядтардың өрістерінің кернеуліктірінің қосындысына тең
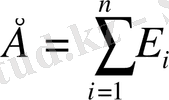
Сондықтан
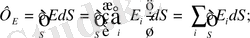
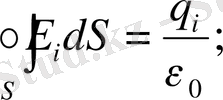 олай болса
олай болса
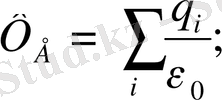 (1. 9)
(1. 9)
Сонда Гаусс теоремасы былай оқылады: кез-келген тұйық бетті қиып өтетін электр өрісінің кернеулік векторының ағыны сол беттің ішіндегі зарядтардың қосындысын
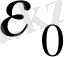 -ге бөлгенге тең.
-ге бөлгенге тең.
Жалпы жағдайда тұйық беттің ішіндегі зарядтардың алып жатқан көлемі V болса, онда зарядтың тығыздығы
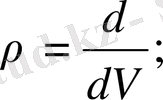
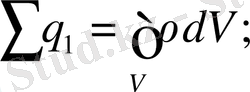
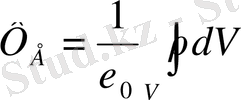 болады.
болады.
Гаусс теоремасын пайдаланып әртүрлі жағдайдағы зарядтың, немесе зарядтар системасының өрістерінің кернеуліктерін анықтауға болады.
Электр өрісінің кернеулік векторының циркуляциясы. Нүктелік q зарядының өөрісінде q 0 нүктелік заряды 1 нүктеден 2 нүктеге орын ауыстырсын. Сондағы электр өрісінің зарядқа әсер еткен күшінің істейтін элементар жұмысы
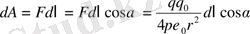 (1. 10)
(1. 10)
мұнда
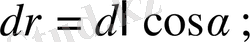
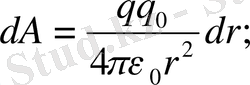 (1. 11)
(1. 11)
толық жұмыс
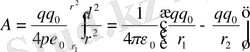 (1. 12)
(1. 12)
(1. 13) формуладан электр өрісінде істелген жұмыстың шамасы жүрілген жолға байланыссыз, тек зарядтың бастапқы және соңғы орындарына тәуелді екендігін көреміз. Олай болса, электростатикалық өріс потенциалды өріс болады. Потенциалды өрісте зарядқа әсер ететін күш консервативтік күш болады. (1. 13) формуладан электр өрісінде тұйық контурдың бойымен істелген жұмыс нульге тең болатынын көреміз.
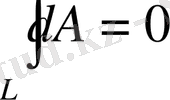 (1. 14)
(1. 14)
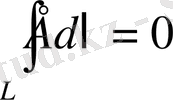 бұл интегралды кернеулік векторының циркуляциясы дейміз.
бұл интегралды кернеулік векторының циркуляциясы дейміз.
Дөңгелек контурдың бойындағы электр өрісінің кернеулік векторының циркуляциясы әр уақытта нульге тең болады.
Бұл электр өрісінің кернеулік сызықтарының тұйықталмайтындығын, тек зарядтан басталып, зарядқа аяқталатынын көрсетеді немесе шексізге кететіндігін көреміз.
Электр өрісінің потенциалы. Потенциалды (электр өрісі потенциалды) өрісте дененің потенциалдық энергиясы болады. Сондықтан потенциалды электр өрісінде заряд орын ауыстырғандағы істелген жұмысы сол зарядтың бастапқы және соңғы нүктелеріндегі потенциалдық энергиясының айырмасына тең болады.
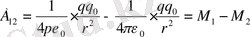
Осыдан q 0 зарядының q заряд өрісіндегі потенциалдық энергиясы:
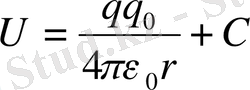 (1. 15)
(1. 15)
егер
 болса,
болса,
 онда
онда
 сонда
сонда
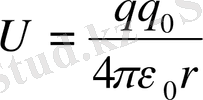 (1. 16)
(1. 16)
Енді q зарядтан r арақашықтықтағы нүктесіндегі өрістің потенциалын анықтайық. Ал сол нүктеге кезекпе-кезек сыншы зарядтар қойып олардың потенциалдық энергияларын анықтайық.
 (1. 17)
(1. 17)
 - өрістің потенциалы.
- өрістің потенциалы.
Өрістің потенциалы деп, өрістің сол нүктесіне қойылған бірлік оң зарядтар потенциалық энергиясына тең физикалық шаманы айтады. Енді потенциал ұғымын пайдаланып q 0 зарядты өрістің істейтін жұмысын былай жазуға болады.
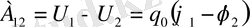 (1. 18)
(1. 18)
q
0
зарядын өрістің бір нүктесінен шексіздікке дейін көшіргенде істелетін жұмыс
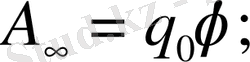
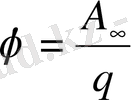
осыдан бірлік зарядты өрістің бір нүктесінен шексіздікке көшіргенде істелетін жұмыс пен өлшенетін физикалық шаманы өрістің потенциалы дейміз
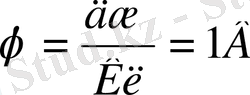
Бірнеше зарядтардың өрісінің бір нүктесіндегі потенциалы, сол нүктедегі әрбір зарядтың потенциалдарының алгебралық қосындысына тең болады:
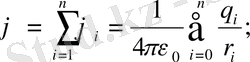 (1. 19)
(1. 19)
Кернеу потенциалдарының градиенті. Эквипотенциалдық беттер. Өрістің күштік күйін сипаттайтын кернеулігімен, оның энергетикалық күйін сипаттайтын потенциалының арасындағы байланысты қарастырайық.
Бірлік оң зарядты өрісте dx арақашықтыққа орын ауыстырғанда, өрістің істейтін жұмысы dA =F
x
dx. Екінші жағынан бұл жұмыс
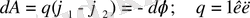 осыдан
осыдан
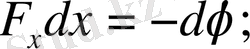
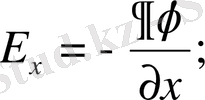
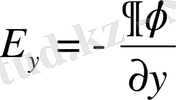 ;
;
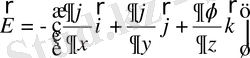 (1. 20)
(1. 20)
мұндағы
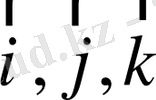 - бірлік векторлары.
- бірлік векторлары.
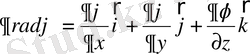
мұндағы
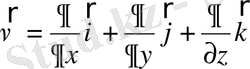 -
Лаплас операторы
-
Лаплас операторы
Сонымен
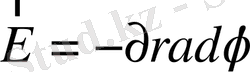 (1. 21)
(1. 21)
минус таңбасы өрістің кернеулігі әр уақытта, оның потенциалының кему бағытына қарай бағытталатындығын көрсетеді. Нүктелік зарядтың электростатикалық өрісі концентрлі шеңберлер болады. Оның потенциалы
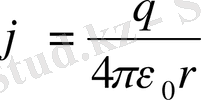 ;
;
Бұл оның радиусы тең шеңбердің барлық нүктелеріндегі потенуциалдары өзара тең болатындығын көрсетеді. Осындай потенциалдары бірдей беттерді эквипотенциалды беттер дейді. Экваипотенциалды беттер мен зарядтар орын ауыстырған кезде істелетін жұмыс нулге тең болады. Өрістің кернеулік векторының күш сызықтары эквипотенциалды беттерге әруақытта перпендикуляр болады.
Электр өрісіндегі өткізгіштер. Электр сыйымдылық. Өткізгіш сыртқы электр өрісінде тұрса электр өрісінің әсерінен, оның еркін зарядтары қозғалысқа келеді. Сыртқы өрістің кернеулігінің бағытында оң зарядтар, ал кернеуліктің бағытына қарама қарсы бағытта теріс зарядтар қозғалады.
Сүйтіп, бар зарядтар орын ауыстырып болған соң, зарядтардың қозғалысы тоқтайды да өткізгіштің ішінде. Сыртқы өрістің бағытына қарама -қарсы
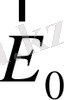 өріс пайда болады. Осы екі өріс бірін -бірі теңестіріп, өткізгіштің ішіндегі қорытқы өріс нулге тең болады.
өріс пайда болады. Осы екі өріс бірін -бірі теңестіріп, өткізгіштің ішіндегі қорытқы өріс нулге тең болады.
Өткізгіштегі зарядтар сыртқы өрістің әсерінен өткізгіштің беткі қабатында орналасады.
Егер өткізгішке бір q заряды берілсе, онда ал өткізгіштің ішіндегі өріс кернеулігі
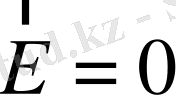 болатындай таралады. Сонда өткізгіш бетінің кез келген екі нүктесіндегі заряд тығыздықтарының қатынасы зарядтың кезкелген шамасы үшін бірдей болады.
болатындай таралады. Сонда өткізгіш бетінің кез келген екі нүктесіндегі заряд тығыздықтарының қатынасы зарядтың кезкелген шамасы үшін бірдей болады.
Бұдан оң аталынған өткізгіштің потенциалы ондағы бар зарядқа пропорционал болатынын көруге болады. Мысалы, өткізгіштегі зарядты қанша есе артырсақ, онда өрістің әрбір нүктесіндегі кернеулігінің де сонша есеге артатынын байқаймыз.
Сонымен оқшауланған өткізгіш үшін:
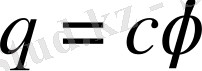 ; (1. 22)
; (1. 22)
С - пропорционалдық коэффициент өткізгіштің электр сыйымдылығы:
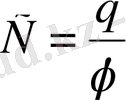 ; (1. 23)
; (1. 23)
Сонымен, сыйымдылық сан жағынан өткізгіштің потенциалын бір өлшемге арттыруға қажетті зарядқа тең екен.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz