Эйлерлік графтың кейбір есептерінің теориясы

1. Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

2. Негізгі бөлім ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2.1. Граф ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2.2. Толық граф ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2.3. Логикалық есептерді граф арқылы есептеу ... ... ... ... ..

2.4 Эйлерлік графтар ... ... ... ... ... ... ... ... ... ... ... ... ... .

3.Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

4.Пайданылған әдебиет ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

"Эйлерлік графтың кейбір есептерінің теориясы" тақырыбы бойынша көптеген нүктелерді жүргізе отырып, әр түрлі фигураларды құрастырамыз. Соның салдарынан "граф" ұғымы пайда болған. "Граф" деп кез-келген нүктелерді, яғни олардың түзумен немесе бағыттауыштармен (стрелка) байланысқаны. Көптеген элементтерді бейнелейтін нүктелерді "граф шыңы" деп атайды. Егер бағыттауыштардың(стрелка) басы мен соңы теңессе, онда оны дәнекер деп атайды.
Граф теориясы математиканың логика, комбинаторика, тағы басқа салаларында қолданылады. Сондықтан бұл тақырыпты мектепте оқыту жалпы білім беретін, мәдениет танытатын, математикалық мән-мағынасы ерекше. Күнделікті өмірде көптеген графикалық иллюстрацияларды, геометриялық елестерді және т.б. көптеген тәсілдер пайдаланылады
Студенттерге әрбір логикалық пікірдің дәмін сезіне білу керек және бұл жерде графтарды қолдану логикаға назарын аударуға көмектеседі. Графтардың түзулері қабырғалары деп, ал нүктелері төбелері деп аталады. Графтардың төбелері тек нүктемен ғана емес, сонымен қатар, дөңгелектермен немесе басқа да фигуралармен берілуі мүмкін.
Студент граф арқылы есеп шығара отырып, өзінің логикасын дамытады. Есептерді граф арқылы шешуді есеп шығару кезінде қолдана білсе, онда олардың пәнге деген қызығушылығы артады.

1. Акентьев В., Со второго взгляда, "Лениздат",1969 ж.
2. Линьков Г.И. , Внеклассная работа по математике , "Просвещение", 1965 ж
3.Нагибин Ф.Ф., Математическая шкатулка, "Просвещение", 1988 ж.
4.Оре О., Графы и их применение, "Мир", 1965 ж.
5.Перельман Я.И., Живая математика, "Наука", 1978 ж.

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Мазмұны

1. Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ..

2. Негізгі бөлім ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2.1. Граф ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

2.2. Толық граф
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ..

2.3. Логикалық есептерді граф арқылы есептеу ... ... ... ... ..

2.4 Эйлерлік графтар ... ... ... ... ... ... ... ... ... ... ... ... ... .

3.Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... .

4.Пайданылған әдебиет ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

I. Кіріспе

"Эйлерлік графтың кейбір есептерінің теориясы" тақырыбы бойынша
көптеген нүктелерді жүргізе отырып, әр түрлі фигураларды құрастырамыз.
Соның салдарынан "граф" ұғымы пайда болған. "Граф" деп кез-келген
нүктелерді, яғни олардың түзумен немесе бағыттауыштармен (стрелка)
байланысқаны. Көптеген элементтерді бейнелейтін нүктелерді "граф шыңы" деп
атайды. Егер бағыттауыштардың(стрелка) басы мен соңы теңессе, онда оны
дәнекер деп атайды.
Граф теориясы математиканың логика, комбинаторика, тағы басқа
салаларында қолданылады. Сондықтан бұл тақырыпты мектепте оқыту жалпы
білім беретін, мәдениет танытатын, математикалық мән-мағынасы ерекше.
Күнделікті өмірде көптеген графикалық иллюстрацияларды, геометриялық
елестерді және т.б. көптеген тәсілдер пайдаланылады
Студенттерге әрбір логикалық пікірдің дәмін сезіне білу керек және
бұл жерде графтарды қолдану логикаға назарын аударуға көмектеседі.
Графтардың түзулері қабырғалары деп, ал нүктелері төбелері деп аталады.
Графтардың төбелері тек нүктемен ғана емес, сонымен қатар,
дөңгелектермен немесе басқа да фигуралармен берілуі мүмкін.
Студент граф арқылы есеп шығара отырып, өзінің логикасын дамытады.
Есептерді граф арқылы шешуді есеп шығару кезінде қолдана білсе, онда
олардың пәнге деген қызығушылығы артады.

II. Негізгі бөлім

2.1 Граф

"Граф" сөзі математикалық әдебиетте жаңадан пайда болған ұғым. Сонымен
қатар, граф тек қана математикада ғана қолданылып қоймай, тіпті техника
мен күнделікті өмірде де басқа атаулармен (схема, диаграмма,т.б) кездеседі.
Әсіресе граф көптеген логикалық есептерді шығаруда көмектеседі.
Графтар есептерді немесе олардың шығару жолдарын адам есіне лезде сақтап
алуы үшін де қолданылады.
Логикалық есептер адамның ойлау қабілеттігін арттырады.
Оқушыларға әрбір логикалық пікірдің дәмін сезіне білу керек және бұл
жерде графтарды қолдану логикаға назарын аударуға көмектеседі. Графтардың
түзулері қабырғалары деп, ал нүктелері төбелері деп аталады. Графтардың
төбелері тек нүктемен ғана емес, сонымен қатар, дөңгелектермен немесе
басқа да фигуралармен берілуі мүмкін.
Граф теориясы математиканың логика, комбинаторика, тағы басқа
салаларында қолданылады. Сондықтан бұл тақырыпты мектепте оқыту жалпы
білім беретін, мәдениет танытатын, математикалық мән-мағынасы ерекше.
Күнделікті өмірде көптеген графикалық иллюстрацияларды, геометриялық
елестерді және т.б. көптеген тәсілдер пайдаланылады

Кенигсберг көпірі жайындағы есепті алғаш рет Л.Эйлер (1707-1783) графтар
теориясы арқылы қарастырды. Бұдан 100 жыл өткен соң әсіресе Англияда
жаратылыстану ғылымының барынша әр түрлі формадағы саласында гарфтар
теориясы қолданыла бастады. Электр тізбегі мен кристалл моделін молекуланың
структурасын зерттеуге, сондай-ақ ойындар теориясы мен программалауда,
биология мен психологияда кеңінен қолданылды.

Граф - Граф (грекше-жазамын) – төбелер деп аталатын шектеулі нүктелерддің
жиынтығы;төберлердің кейбіреулері графтың қырлары деп аталатын сызықтарымен
байланысқан болады. Төбелердің жиыны (v) және реттелмеген және реттелген
төбелердің (қырлар мен доғалар) жиынтығы (e) граф болып табылады: Граф “G”
(V,E) болып белгілінеді. Тек қырлары ғана қамтитын граф – бағдарланбаған,
ал тек доғаларды қамтитыны бағдарланған граф деп аталады. Кез – келген екі
төбені қосатын тізбегі болатын граф – байланысқан граф болып табылады.

Граф — нысандар мен олардың арасындағы байланыстар жиынтығын айтады.
Нысандар графтың төбелері деп, ал байланыстар граф қабырғалары деп аталады.
Графты қолданылатын саласына байланысты байланыстар саны, қабырғалар
бағытымен және төбелеріндегі әртекті қасиеттерімен ажыратады. Көптеген
есептерді, нысандарды графтармен сипаттауға болады. Мысалға Уикипедияны да
графпен сипаттауға болады — төбелері мақалалар, ал қабырғалары —
гиперсілтемелер

Граф, немесе бағытталмаған граф  — бұл 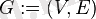 келесі шарттарды
қанағаттандыратын ретті жұптар жиынтығы:

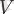• — төбелер немесе түйіндер бос емес жиыны ;
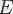• — қабырғалар деп аталатын төбелерден құралған жұптар
(бағытталмаған графта — ретсіз).

Төбелері мен қабырғаларын кейде граф элементтері деп те атайды, граф
төбелер санын 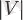 — граф дәрежесі, қабырғалар санын  —
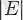графөлшемі деп атайды.

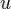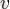және  төбелері 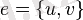 қабырғасының шеткі төбелері
(немесе шеттері) деп аталады. Бір қабырғаның екі шеткі
төбелері көршілес деп атады.

Ортақ шеткі төбелері бар екі қабырға түйіндес деп аталды.

Шеткі төбелер жиыны бірдей болатын екі қабырға еселі деп аталады.

Шеткі төбелер беттесетін қабырғаны ілмек аталыды, яғни 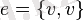 болса.

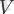төбесінің дәрежесі 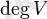 деп оған тірелетін қабырғалар санын айтады
(ілмекті екі рет санайды).

Төбе ешқандай қабырғаның шеті болмаса оңашаланған болады; ал егер тек қана
бір қабырға шеті болса салбыраулы (немесе жапырақ) болады.

Графтар арқылы кейбір есептерді шешуге болады.
1-есеп: Үш дос- Серік, Талғат, Ернар әр түрлі үш пәннен (химия,
биология, физика) Алматының, Қарағандының, Көкшетаудың мектептерінде
оқытады. Егер мына мәліметтер белгілі болса: 1) Серік Алматыда істемейді,
ал Талғат Қарағандыда
тұрмайды; 2) Алматылық физикадан сабақ бермейді; 3) Қарағандыда тұратын
мұғалім
химиядан сабақ береді; 4) Талғат биологиядан сабақ бермейді. Әр мұғалім
қай қалада тұрады, қандай пәннен сабақ береді?
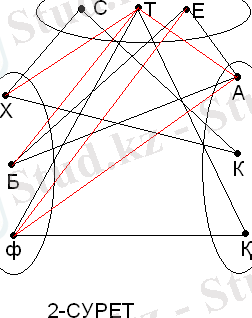
Шешуі:Үш жиын алып, олардан үштен нүкте қарастырамыз. Оларды адамдар
аттарының бас әріптері, пәндер мен қалалардың аттарының бірінші әріптерімен
белгілейміз. Әр түрлі жиыннан алынған нүктелер бір ғана адамның қасиеттерін
бейнелей алса, онда ол нүктелерді тұтас (үзіксіз) сызықтармен қосамыз, егер
олар әр түрлі адамның белгілерін білдірсе, үзік сызықтармен (штрихтармен)
қосамыз. Үзік-қызыл, ал тұтас – қара түспен сызамыз. Есептің берілгендері
1 –суретте:

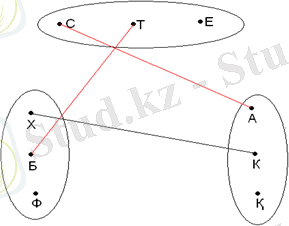
1-СУРЕТ

Граф есеп шартында көрсетілген жиын элементі және олардың арасындағы
байланыс болады. Бұл есеп граф тілінде төбелері үш жиында жатқан,
қабырғалары тұтас сы-зықтармен қосылған үш үшбұрышты салуға келтіреледі.
ХТ- сәйкес келмейді, Х мен Т-ны қызыл сызықпен қосамыз, ол КХ сәйкес келеді
(Көкшетауда тұратын мұғалім химиядан береді), Т мен К сәйкес келмейді – ТК,
сондықтан Т мен Х сәйкес келмейді (2-суретте).
Граф арқылы осы есепке ұқсас есепті шешкенде мынадай ережелерді
пайдаланамыз: 1) Үш төбесі үш жиында жатқан үщбұрыштың бір қабырғасы тұтас
(қара) сызықпен, екіншісі үзік(қызыл) сызықпен сызылса, онда үшінші
қабырғасы үзік (қызыл) сызықпен сызылады; 2) Жиыннның бір нүктесінен 2-
жиындағы 2-нүктеге үзік (қызыл) сызық жүргізілсе, онда үшіншісіне тұтас
(қара) сызық жүргізіледі; 3) Егер төбелері әр түрлі жиында жатқан
үшбұрыштың екі қабырғасы тұтас (қара) сызықпен сызылса, онда үшіншісі де
тұтас (қара) сызықпен қосылады.
Ережеге сүйеніп Ф мен Т-ны тұтас сызықпен қосамыз (ФТ). АТ- үзік сызықпен
сызылады, себебі ТФА үшбұршында ТФ –тұтас, ФА- үзік сызықтармен сызылады.
ТҚ тұтас сызықпен қосылады, себебі ТА,ТК- үзік сызықтар. ФҚ- тұтас сызық.
Олай болса,
ТФҚ-үшбұрышының қабырғалары тұтас сызық болады. АЕ,СК,ХС, БА, БЕ-тұтас
сызықтарын жүргіземіз. Сонда ТФҚ, КХС және ЕАБ- үшбұрышының төбелеріндегі
элементтер сәйкес келіп,есептің сұрағына жауап береді, яғни Ернар- биолог
Алматыда тұрады; Серік - Көкшетауда тұрып, химиядан сабақ береді; Талғат
Қарағандыда тұрады, физикадан сабақ беред.

2-есеп: Дүйсенбі күнгі сабақ кестесін құру кезінде үш мұғалім мынадай
өтініш айтты: 1) математика бірінші не екінші, 2) тарих бірінші не үшінші,
3) әдебиет екінші не үшінші болсын.
Қанша тәсілмен мұғалім өтінішін орындауға болады?

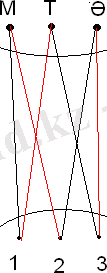
3-СУРЕТ

Шешуі: Математика, тарих, әдебиеттің бас әріптерінен бір жиын сабақтардың
1,2,3 –деген ретінен екінші жиын құралық (3-сурет))
Математиканы 1-сабаққа (онда ол 2-бола алмайды) қойсақ, онда тарих тек
үшніші ғана болады, тарих 1-қойылмайды, онда әдебиет 2-сабаққа қойылған
болады, ол 3- сабаққа қойылмайды. Сонымен математика- бірінші, әдебиет-
екінші, тарих-үшінші болады.
Теңдеуді граф арқылы шешу, яғни бұл бағытталған граф болып табылады.
3-есеп: Мен бір сан ойладым. Сол санға 24 қоссақ, одан шыққан санды 9-
ға көбей-тсек, сосын 76- ны алсақ, ендігі шыққан санды 19- ға бөлсек, онда
23 шығады.Ойлаған санды табайық.
((х + 24)*9-76)19=23
9х+140=437
9х=297
х=33
Графты құрайық. Енді осы сандарды керісінше амалмен шығарайық (4-СУРЕТ)
23*19 =437 437+76=513 5139=57 57-24=33. Сонымен ойлаған
санды таптық-33.

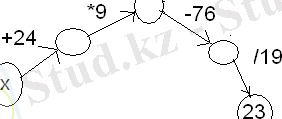
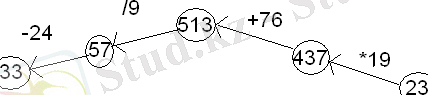
4-СУРЕТ

Математикада ешбір математикалық ережелерді немесе теоремаларды қолдануға
келмейтін, тек ойлау арқылы шығарылатын есептер деп аталады. Осындай
логикалық есертерді, математикалық басқатырғыларды шешуде графтар
қолданылады.
Граф деп қандай да бір берілген пункттерді қосатын сызықтар системасын
айтамыз, яғни әуелі біз берілген обьектілерді нүктелер арқылы кескіндейміз,
оларды берілген шарттар арқылы кескінділермен қосамыз, нүктелер мен
кесінділер арасында операциялар орындаймыз.
Графтар теориясы бас қатырғыларды шешумен байланысты XVIII ғасырда туды.
Графтар теориясынан ең бірінші еңбекті белгілі швед математигі Эйлер 1736
жылы жазды. Әуелгі кезде бұл теория тек топологияның өркендеуіне байланысты
графтар теориясы математиканың бір саласы ретінде ең алғаш ХХ ғасырдың 30
жылдарында венгер математигі Кенигтің еңбегінде айтылады.
4-есеп: Географиялық картаға қарағанда көзге, бірден темір жол желісі
түседі. Бұл негізгі граф: дөңгелектер станция-граф шыңы, ал байланыстыру
жолы-қабырғаны білдіреді.
5-суреттегі граф М,А,Б,В,Г аралықтарындағы кент жолдарының схемасы
көрсетелі. Мұнда әрбір 2 щың қабырғамен байланысады. Мұндай графты толық
граф деп атайды. 5-суреттегі сандар кент жолда5ы арақашықты көрсетеді. М-
кентінде пошта және пошташы қалған 4 кентке хат тарату керек. Жол жүруге
арналған әр түрлі маршруттар бар. Осылардың арасынан ең қысқасын қалай
табамыз? Ең қысқасы бүкіл нұсқаларды нәтижелеу. Мұны істеуге жаңа граф (5-
сурет) ондағы мүмкін маршруттарды жеңіл мүмкіншілікті көретіндей. М-шыңының
үстінде –маршруттар бастамасы. Одан А-ға, Б-ға, В-ға немесе Г-ға осындай
тәсілмен жол бастауға болады. Біреуін қолданған соң ақырында 3-маршрутты
жалғастырудың 3 мүмкіндігі қалады, одан кейін 2, содан соң ең соңғы кент
және қайтадан М-ға. Барлығы 4*3*2*1=24 тәсіл. Олардың барлығы осы графта
көрсетілген.
Кент аралығын білдіретіндей қабырғаларына сандар қоямыз, соңына әрбір
маршруттың соммасын жазамыз. Осыдан шыққан 24 санына екіншісі 2 сан 28 км-
ден, М-В-Б-А-Г-М және М-Г-А-Б-В-М маршруттарына сәйкес келеді. Бұл бірдей
жол, бірақ әр түрлі бағытта жүрілген.

5-СУРЕТ

2.1. Толық граф

Толық граф — кез келген екі төбесі қабырғамен байланысқан қарапайым граф.
Яғни,  төбелі толық графта  қабырғалары бар және бұндай
граф  деп белгіленеді. Дәрежесі  болатындай Жүйелі граф болып
табылады.

ден  ке дейін Планар граф болып табылады. Төбелер саны көп
болатындай толық графтар планар бола алмайды, себебі олар  ішкі
графты қамтиды, сондықтан да Понтрягин-Куратовский теоремасы шарттарын
қанағаттандырмайды.

Төменде төбелер саны 1ден 8ге дейін болатын толық графтар және олардың
қабырғалар саны берілген.

: 0 : 1 : 3 : 6
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.