Магниттік резонанс: негізгі теория, Блох теңдеулері, релаксация және спектрлік қолданбалар


Қазақстан Республикасының білім және ғылым министрлігі Шәкәрім атындағы Семей мемлекеттік университеті
сөж
Тақырыбы: Магниттік резонанс.
Орындаған: Қабышев Е. М
Топ: т-323
Тексерген: Мешетова Ж. С
2015ж
Магниттік резонанс.
Магниттік резонанс құбылыстары қазіргі физика, химия, биологияда жəне т . т. елеулі рөл атқарады. Өйткені бұлар заттың құрылысын, қасиеттерін зерттеудің өте тиімді амалы болып табылады. Магниттік резонанс құбылысының мəнісін атомдардың магниттік қасиеттері жəне бұлардың сыртқы магнит өрістерімен де, бірімен-бірінің де əсерлесуі жөніндегі деректерге сүйеніп оңай түсінуге болады.
Магниттік резонанс - зат бөлшектерінің (электрондардың, атом ядроларының) магниттік моменттері бағдарларының өзгеруіне байланысты заттың белгілі бір жиіліктегі ) барμ) электрмагниттік толқындарды таңдап жұтуы. Магниттік моменті (ω( бөлшектің энергетикалық деңгейлері сыртқы магнит өрісінде (Н) магниттік қосалқы деңгейлерге жіктеледі; олардың әрқайсысына магнит өрісіне (Н) қатысты магнит моменттің белгілі бір бағдары сәйкес келеді (қ. Зееман эффектісі) электр-магниттік өріс қосалқы магнит деңгейлер арасындаω) . Резонанстық жиіліктегі ( кванттық ауысу туғызады. Резонанс шарты:
- түрінде жазыладыω=∆
мұндағы
- - магнит қосалқы деңгейлер арасындағы энергия айырымы. ∆
Егер элетр-магниттік энергияны жұту процесі ядролар арқылы жүзеге асса, онда Магниттік резонанс ядролық магниттік резонанс (ЯМР) деп аталады. Парамагнит атомындағы қосарланбаған электрондардың магнит моменті нәтижесінде пайда болатын Магниттік резонансты электрондық парамагниттік резонанс (ЭПР) деп атайды. Магнит реттелген заттардағы электрондық Магниттік резонанс ферромагнит және антиферромагнит 103-104) ЯМР-дың жиіліктері қысқа∼Магниттік резонанс деп аталады. Әдетте, қолданылатын магнит өрістерде ( радиотолқындар диапазонына (106-107Гц), ал ЭПР жиіліктері аса жоғары жиілік диапазонына (109 - 1010Гц) орналасады. Магниттік резонанстың спектрлері затта әсер ететін әр түрлі ішкі өрістерге сезімтал келеді. Сондықтан Магниттік резонанс қатты денелердің және сұйықтықтардың құрылымын, атом және молекулалық динамиканы, т. б. зерттеу үшін қолданылады.
μ
магниттік моментке және
 қозғалыс мөлшері моментіге ие ядроны қарастырайық. Бұл моменттер параллель, сондықтан оларды келесі түрде жазуға болады:
қозғалыс мөлшері моментіге ие ядроны қарастырайық. Бұл моменттер параллель, сондықтан оларды келесі түрде жазуға болады:
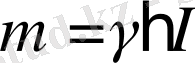 (1)
(1)
мұндағы,
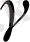 магнитомеханикалық қатынас - тұрақты шама.
I
арқылы
магнитомеханикалық қатынас - тұрақты шама.
I
арқылы
 бірліктерінде өлшенген қозғалыс мөлшерінің ядролық моментін белгілеу негізіне алынған. μ магниттік момент пен
В
а
сыртқы магниттік өрістің әсерлесу энергиясы:
бірліктерінде өлшенген қозғалыс мөлшерінің ядролық моментін белгілеу негізіне алынған. μ магниттік момент пен
В
а
сыртқы магниттік өрістің әсерлесу энергиясы:
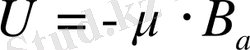 ; (2)
; (2)
Егер де өріс
z
осі байынша бағытталған болса, яғни:
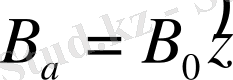 , онда
, онда
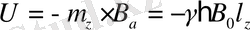 (3)
(3)
I
z
рұқсат етілген мәндері :
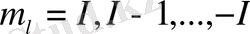 , демек, энергияның рұқсат етілген мәндері:
, демек, энергияның рұқсат етілген мәндері:
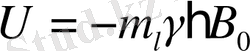 (4)
(4)
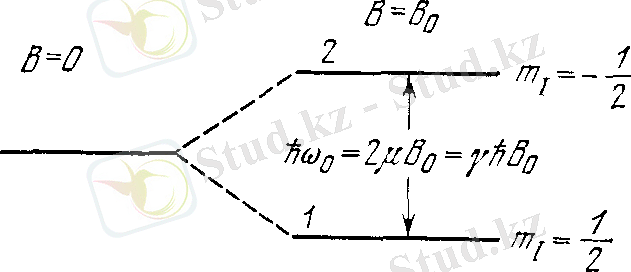
2 сурет. I=1/2 спинді ядролардың B 0 тұрақты магниті өрісіндегі энергетикалық деңгейлердің ыдырауы.
I=1/2
болатын магнит өрісінде жататын ядро,
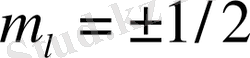 -ге сәйкес келетін екі энергетикалық деңгейде жатуы мүмкін. Егер де осы күйлердегі энергиялардың айырмашылығы
-ге сәйкес келетін екі энергетикалық деңгейде жатуы мүмкін. Егер де осы күйлердегі энергиялардың айырмашылығы
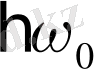 -ге теңесек, онда
-ге теңесек, онда
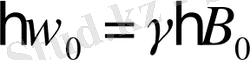 , демек,
, демек,
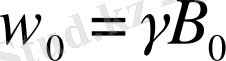 (4)
(4)
Бұл қатынас магниттік резонансты жұтылудың негізгі шарты болып келеді.
Протон жағдайында (протонның магниттік моменті
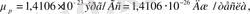 және
және
 ) .
) .
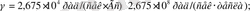 демек, жиілік үшін :
демек, жиілік үшін :
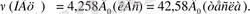 (4а)
(4а)
Бір тесла 10 4 Гс-ке тең. Электрон спині үшін:
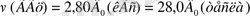 (4б)
(4б)
Магниттік резонанс құбылыстары үшін элемент ядролар туралы ақпараттар 1 кестеде келтірілген.
Қозғалыс теңдеулері.
Уақыт өткен сайын жүйенің қозғалыс мөлшерінің өзгеруі жүйеге әсер ететін бұрыштық моментке тең екені белгілі.
В
Магнит өрісінен
μ
магниттік моментке әсер ететін механикалық момент
 векторлық көбейтіндіге тең. Онда, момент үшін («гироскопиялық теңдеу») қозғалыс теңдеуін келесі түрде жазуға болады:
векторлық көбейтіндіге тең. Онда, момент үшін («гироскопиялық теңдеу») қозғалыс теңдеуін келесі түрде жазуға болады:
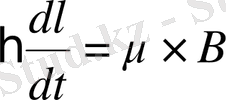 (5)
(5)
Немесе
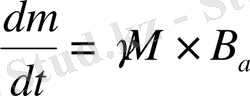 (6)
(6)
М
ядролық магниттелу көлем бірілігінде барлық ядролар бойынша
 сома ретінде анықталады. Егер де бір изотопты ядролар қарастырылса және олар тек өріспен әсерлескенде, онда γ коэффициенті барлық ядролар үшін бірдей және (6) теңдеуді
М
үшін жазуға болады:
сома ретінде анықталады. Егер де бір изотопты ядролар қарастырылса және олар тек өріспен әсерлескенде, онда γ коэффициенті барлық ядролар үшін бірдей және (6) теңдеуді
М
үшін жазуға болады:
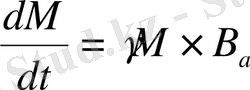 (7)
(7)
Ядролар жүйесін
z
осі бойымен бағытталған
В
а
магниттік өріске енгіземіз, яғни
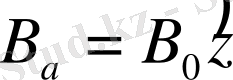 .
Т
температурада жылулық тепе-теңдік кезінде
М
магниттелу компоненттері үшін:
.
Т
температурада жылулық тепе-теңдік кезінде
М
магниттелу компоненттері үшін:
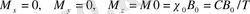 (8)
(8)
Мұндағы
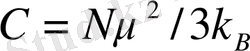 - Кюри тұрақтысы, (15. 14) тұрақтының анықтауы бойынша.
I=1/2
-мен спиндер жүйесінің магниттелуі 1 және 2 деңгейлердің
N
1
-N
2
айырмашылығымен анықталады. Толтыру қатынасы жылулық тепе-теңдіктегі Больцман үлестіруімен беріледі:
- Кюри тұрақтысы, (15. 14) тұрақтының анықтауы бойынша.
I=1/2
-мен спиндер жүйесінің магниттелуі 1 және 2 деңгейлердің
N
1
-N
2
айырмашылығымен анықталады. Толтыру қатынасы жылулық тепе-теңдіктегі Больцман үлестіруімен беріледі:
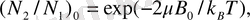 (9)
(9)
1 және 2 күйлердегі энергиялар айырмасы
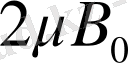 -ға тең болғандықтан, тепе-теңдік кезіндегі магниттелу шамасы (15. 20) формуласымен анықталады,
-ға тең болғандықтан, тепе-теңдік кезіндегі магниттелу шамасы (15. 20) формуласымен анықталады,
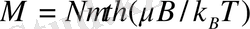 , мұндағы, бірақ та,
μ -
ядролық магнит моменті.
, мұндағы, бірақ та,
μ -
ядролық магнит моменті.
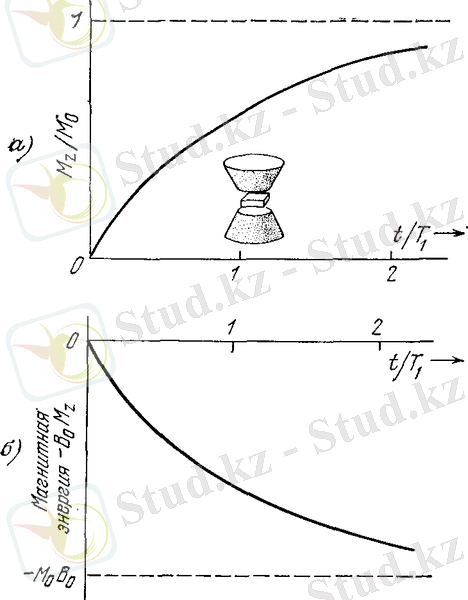
3 сурет. а) Магниттелудің уақыт өткен сайын өрістің қосқан кездегі өзгеруі.
t=0
уақыт кезіндегі
M
z
(0) =0
-мен магниттелмеген үлгі
В
0
магнит өріске енгізіледі. Магниттелу уақыт сайын өседі және жаңа тепе-теңдіктің
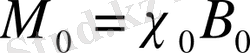 жаңа мәніне жетеді . Бұл эксперимент
Т
1
шамасын- бойлық релаксацияның уақытын анықтайды.
б)
Уақыт өткен сайын жүйенің магнитті энергияның өзгеруі.
а
суретімен байланысқан экспериментте, магниттік энергияның тығыздығы
жаңа мәніне жетеді . Бұл эксперимент
Т
1
шамасын- бойлық релаксацияның уақытын анықтайды.
б)
Уақыт өткен сайын жүйенің магнитті энергияның өзгеруі.
а
суретімен байланысқан экспериментте, магниттік энергияның тығыздығы
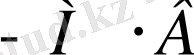 төменгі деңгейдің спиндік толтырылуы жоғарылаған сайын төмендейді.
төменгі деңгейдің спиндік толтырылуы жоғарылаған сайын төмендейді.
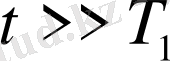 кезінде жететін асимптотикалық мән
кезінде жететін асимптотикалық мән
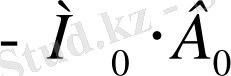 -ға тең. Энергия спин жүйесінен тордың тербелістер жүйесіне өтеді, сол себепті Т
1
релаксация уақытын
спин-торды релаксацияның уақыты
деп атайды.
-ға тең. Энергия спин жүйесінен тордың тербелістер жүйесіне өтеді, сол себепті Т
1
релаксация уақытын
спин-торды релаксацияның уақыты
деп атайды.
Егер
 шамасы тепе-теңсіз күйге қатысты болса, онда біз оның тепе-теңдік күйге
шамасы тепе-теңсіз күйге қатысты болса, онда біз оның тепе-теңдік күйге
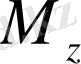 -тің
М
0
тепе-теңдік мәнінен ығысуға пропорционалды «жылдамдықпен» жақындасын делік:
-тің
М
0
тепе-теңдік мәнінен ығысуға пропорционалды «жылдамдықпен» жақындасын делік:
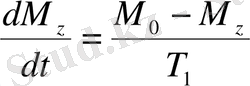 (10)
(10)
Осы теңдеуде енгізілген Т 1 шамасы бойлық релаксацияның уақыты немес спин-толқынды релаксацияның уақыты деп аталады.
Егер де
t=0
алғашқы уақытта магниттелмеген үлгі
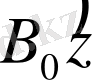 магниттік өріске енгізілген болса, онда оның магниттелуі алғашқы
магниттік өріске енгізілген болса, онда оның магниттелуі алғашқы
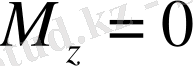 нөлдік мәнінен соңғы мәнге
нөлдік мәнінен соңғы мәнге
 дейін өседі. (10) теңдеуді интегралдасақ:
дейін өседі. (10) теңдеуді интегралдасақ:
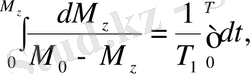 (11)
(11)
немесе
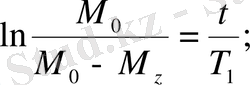
 (12)
(12)
Алынған тәуелділік 3а суретте график арқылы бейнеленеді.
 магниттік энергия
магниттік энергия
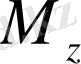 -нің жаңа тепе-теңдік мәнге жақындаған сайын төмендейді. 4 суретте магниттелу өзінің тепе-теңдік мәнге жақындалуы болатын процесстер схемалы түрде көрсетілген.
-нің жаңа тепе-теңдік мәнге жақындаған сайын төмендейді. 4 суретте магниттелу өзінің тепе-теңдік мәнге жақындалуы болатын процесстер схемалы түрде көрсетілген.
Кристаллда парамагнитті иондардың спинді-торды әсерлесу құбылысының мәні ішкі кристал электр өрісі фонондармен модуляциялаумен байланысты. Релаксация негізінен үш процесстермен іске асырылады(4б. сурет) :1) түзу(фонондарды шашырау мен жұту) ; 2) раманов(фононның шашырауы) ; 3) обрахов(қосымша үшінші деңгей қатысуымен шашырау) . Кейбір сирек жер элементтерінің тұздарының спин- торды релаксацияның пысықтауыш- анализі гелийлік температура тұсында Скотт және Джеффрис жұмысында жасалынған. Олар, жеке түрде, жоғарыда көрсетілген барлық процесстер үшін дәлел келтірген және парамагнитті релаксация үшін пайдала әдебиеттер тізімін келтірген. Мысал ретінде, 5 суретте жұмыстың бір нәтижесі көрсетілген.
.
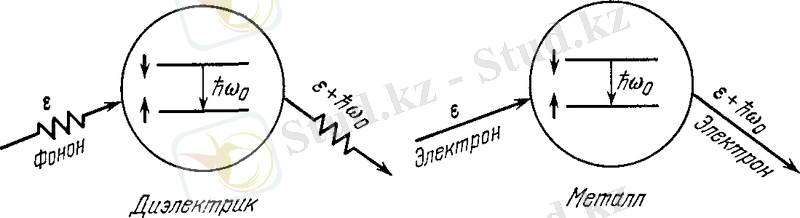
4а. сурет. Металл және диэлектриктегі магниттелудің бойлық релаксациясына үлес беретін маңызды процесстердің жүйесі. Дижлектрике, жүйеде көрсетілгендей, спин жүйесінде фонон серпімсіз шашыратылады, спинді жүйе төмен энергиялы күйге өтеді, осы кезде шығатын фонон жұтылған энергиядан
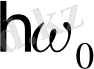 -ге көп энергияға ие. Металлда дәл осындай серпімсіз шашырауының процессі орын алады, бірақ та өткізгіш электроны үшін.
-ге көп энергияға ие. Металлда дәл осындай серпімсіз шашырауының процессі орын алады, бірақ та өткізгіш электроны үшін.
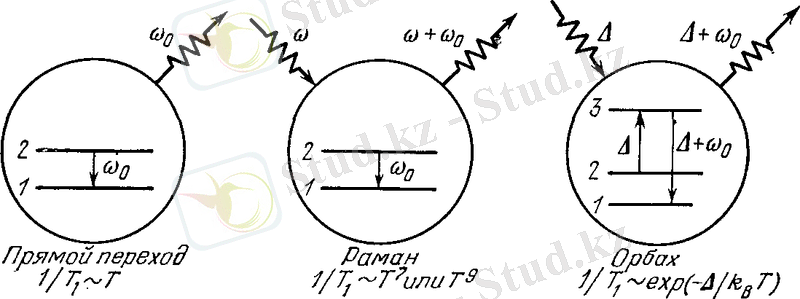
4б. сурет. 2 →1 өтуіне жауап беретін спинді релаксация процессінің жүйесі. Сол жағында- фонон шашырауымен сүйемелденетін процесс(тура ауысу) . Ортасында- фононның раманов шашырауымен байланысты процесс; оң жағында- екі этапта жүретін(Орбах бойынша) фононның шашырауы процессі. Т 1 бойлық релаксацияның уақыттық температуралық тәуелделігінің типі әр процесстің төменінде көрсетілген.
5 сурет. (1% Nd және 5% Nd) неодим қоспасымен, екі нитратты лантан- магний
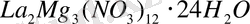 кристаллы үшін
1/Т
1
бойлық релаксацияның шапшаңдылықтың қарсы температурадан тәуелділігі (логарифмдік масштабта) . Бұл нәтижелер Скотт және Джеффриспен
1, 4-4, 3
0
К
температуралар интервалында алынған. Нәтижелер салыстырмалы жоғары температураларда Орбах процессіне және төмен температуралардағы бір фонды процесске көрсетеді.
кристаллы үшін
1/Т
1
бойлық релаксацияның шапшаңдылықтың қарсы температурадан тәуелділігі (логарифмдік масштабта) . Бұл нәтижелер Скотт және Джеффриспен
1, 4-4, 3
0
К
температуралар интервалында алынған. Нәтижелер салыстырмалы жоғары температураларда Орбах процессіне және төмен температуралардағы бір фонды процесске көрсетеді.
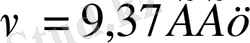 жиілік,
жиілік,
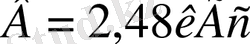 магнит өрісі.
магнит өрісі.
(10) назарына алып, магниттелудің z- компоненті үшін (7) қозғалыс теңдеуін келесі түрде жазуға болады:
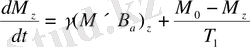 (13а)
(13а)
Мұндағы, ( M 0 -M z ) / T 1 - В а магнитттік өріспен байланысты емесәсерлесулердің нәтижесінде пайда болатын теңдеудің қосымша мүшесі . Осылай, магниттік өрістің айналасындағы прецессиямен қатар, М магниттелу векторы М 0 тепе-теңдік нәтижеге .
Егер тұрақты
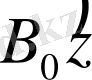 магнит өрісінде
М
х
магниттелу компонентасы нөлге тең болмаса, онда уақыт сайын ол нөлге дейін құлайды. Алғашқы моментте нөлге тең болмайтын
М
бойлық компоненттерінің, яғни
М
х
және
М
у
, нөлге төмендеуінің процесі жылулық тепе-теңдік кезіндегі нөлдік талабына шартталынады.
М
х
және
М
у
үшін қозғалыс теңдеулерінде осы бойлық релаксацияны ескерту үшін қосымша мүшелерді енгізу керек боп тур, қарапайым жағдайда
М
х
және
М
у
шамаларына пропорционал:
магнит өрісінде
М
х
магниттелу компонентасы нөлге тең болмаса, онда уақыт сайын ол нөлге дейін құлайды. Алғашқы моментте нөлге тең болмайтын
М
бойлық компоненттерінің, яғни
М
х
және
М
у
, нөлге төмендеуінің процесі жылулық тепе-теңдік кезіндегі нөлдік талабына шартталынады.
М
х
және
М
у
үшін қозғалыс теңдеулерінде осы бойлық релаксацияны ескерту үшін қосымша мүшелерді енгізу керек боп тур, қарапайым жағдайда
М
х
және
М
у
шамаларына пропорционал:
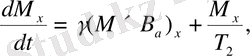 (13б)
(13б)
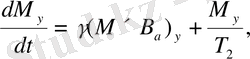 (13в)
(13в)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz