Регрессия коэффициентінің экономикалық түсіндірмесі

Пән: Экономика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

ОӨЖ

Регрессия коэффициентінің экономикалық түсіндірмесі

Орындаған: Қадырова Ж. Р.

Тобы: УА-303

Тексерген: Жаксыгулова Д. Д

Семей 2015 жыл

Жоспар

Кіріспе

Негізгі бөлім

Экономикалық - статистикалық мәліметтердің регрессиялық талдауы

Регрессия коэффициентінің экономикалық түсіндірмесін мысал арқылы көрсету

Қорытынды

Пайдаланылған әдебиеттер тізімі

Экономикалық - статистикалық мәліметтердің регрессиялық талдауы

Экономика, статистика сияқты ғылымдар өздік ғылым болып қалыптасқаннан бері зерттеушілер экономикалық-статистикалық дамудың болжамдарын көрсету арқылы экономикалық жағдайларға ықпал етуге тырысты. Бір түрлі экономикалық жағдай дәл солай екінші рет қайталанбайды деп айтуға болады, себебі бір шартта екі стратегияны қолдану мүмкін емес. Сондықтан экономикалық-статистикалық талдаудың негізгі міндеттерінің бірі экономикалық объектінің дамуын болжау. Кез-келген экономикалық-статистикалық көрсеткіш көптеген факторларға тәуелді. Экономикалық модель құруда олардың бәрін қамту мүмкін емес. Әдетте зерттелетін экономикалық-статистикалық көрсеткішке нақты әсер ететін шектелген факторлар алынады, ал ескерілмеген факторлар экономикалық-статистикалық көрсеткіштерге ауытқулар енгізбейді.

Регрессиялық талдау экономикалық-статистикалық талдаудың келесі қадамы болып табылады және бір немесе бірнеше кездейсоқ шамалардың мәндеріне негізделетін кездейсоқ шаманың мәнін алдын ала айтуға мүмкіндік береді. Бұл мақсатқа Y тәуелді кездейсоқ шамасының (оны бұл жағдайда нәтижелік белгісі деп атайды) Х 1, Х2, . . . , Х М тәуелсіз кездейсоқ шамаларымен (оларды факторлар деп атайды) байланысын сипаттайтын аналитикалық өрнектің түрін анықтау арқылы ғана жетуге мүмкін болады. Y нәтижелік белгісінің Х 1, Х2, . . . , ХМ факторларымен байланыс формасын регрессия теңдеуі деп атайды. Таңдалған теңдеудің типіне байланысты сызықтық және сызықтық емес регрессияны ажыратады (мысалы, квадраттық, логарифмдік, экспоненциалдық және т. б. ) . Регрессия жұптық (қарапайым) және жиынтықтық болуы мүмкін, бұл өзара байланысқан белгілердің санымен анықталады. Егер екі белгілердің (нәтижелік және факторлық) арасындағы байланыс зерттелетін болса, онда регрессия жұптық деп аталады; бұл типке, мысалы, сату мен жарнамаға кететін шығын арасындағы байланысты зерттеу жатады. Егер үш немесе одан да көп белгілердің арасындағы байланыс зерттелсе, онда регрессия жиынтықтық (көпфакторлы) деп аталады, мысалы, егер тұтыну деңгейі, пайда, қаржылық жағдай және жанұя мөлшері арасындағы байланыс зерттелетін болса.

Регрессиялық талдау кезінде келесі негізгі мәселелер шешіледі:

1. Регрессия теңдеуінің жалпы түрін таңдау және регрессия параметрлерін анықтау.

2. Регрессия ішіндегі нәтижелік белгі мен факторлар арасындағы өзара байланыс дәрежесін анықтау, регрессия теңдеуінің жалпы сапасын тексеру.

3. Регрессия теңдеуінің әр коэффициентінің статистикалық маңыздылығын тексеру және олардың сенімділік аралықтарын анықтау.

Қарапайым сызықтық регрессия. Регрессия теңдеуінің жалпы түрін таңдау негізгі мәселе болып табылады, өйткені байланыс формасы Y тәуелді кездейсоқ айнымалысының мәндерін алудың механизмін айқындайды. Байланыс формасы сызықтық немесе сызықтық емес болуы мүмкін. Сызықтық байланыс сызықтық теңдеумен сипатталады.

Регрессиялық талдау - регрессия теңдеуін анықтау және оның параметрлеріне статистикалық бағалауды енгізу. Регрессиялық талдау олардың параметрлеріне статистикалық бағалауды қосқанда регрессия теңдеуін анықтау нәтижесіне ие. Егер тәуелсіз шама немесе тәуелсіз айнымалылар белгілі болса, онда регрессия теңдеуі тәу елді айнымалының мәнін табады.

Графиктегі көп нүктені талдау қажеттілігінен (көптеген статистикалық деректер), сызықты табу, яғни мүмкіншілікке байланысты осы көп заңдылыққа тікелей әсерін тигізетін (тренд, қарқын) - регрессия сызығын табу қажет. Регрессия теңдеуіне енетін факторлардың санына байланысты регрессияны қарапайым (қос) және көпмүшелді деп бөлуге болады. Бірфакторлы регрессия теңдеуі байланыс сипаттамасы бойынша келесідей бөлінеді:

а) сызықтық: у = а + bх,

мұнда х - тәуелсіз (факторлы) айнымалы, у -тәуелді (нәтижелі) айнымалы, a, b -параметрлер;

б) дәрежелі: у=а∗х ⁿ

в) көрсеткішті: y=a∗b ^x және басқалары.

Жай регрессия - у және х айнымалылары арасындағы модель түрі y= f (x) мұндағы y- тәуелді айнымалы (шешуші фактор ) ; x -тәуелсіз айнымалы (белгі-фактор)
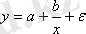Көптік регрессия - қабырғалы гипербола $C:\Users\Zhanar\Desktop\2_clip_image008.gif$ ;
Параметр арқылы бағаланатын регрессия теңдеуі :
•дәрежелі
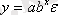• көрсеткішті $C:\Users\Zhanar\Desktop\2_clip_image010.gif$ ;
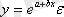
• экспоненциальді $C:\Users\Zhanar\Desktop\2_clip_image012.gif$

Регрессия теңдеуін құру үшін оның параметрлерін анықтау керек. Ол үшін ең кіші квадраттар әдісі қолданылады. Ең кіші квадраттар әдісі бойынша шешуші белгінің нақты мәндерінің тәжірибелік мәндерден ауытқуының қосындысының квадраты минимальді болуы керек, яғни

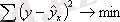
$C:\Users\Zhanar\Desktop\2_clip_image014.gif$

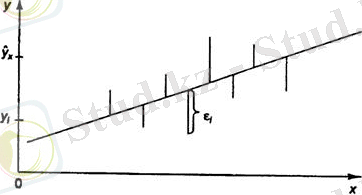
$C:\Users\Zhanar\Desktop\2_clip_image016.jpg$

Сызықты теңдеуге келтірілетін сызықты және сызықты емес теңдеулер үшін а және b -ға қатысты мынадай жүйе шешіледі:

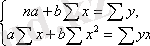
$C:\Users\Zhanar\Desktop\2_clip_image018.gif$
Мына формулаларды қолданамыз.

Анықталатын құбылыстардың байланыс тығыздығын анықтау үшін жұп корреляцияның сызықты регрессия үшін сызықты коэффициентін анықтау керек. (-1 $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ r $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ 1) :

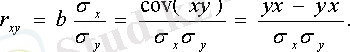
$C:\Users\Zhanar\Desktop\2_clip_image028.gif$
және сызықты емес регрессия үшін корреляция индексін -(0 $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ p $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ 1) :

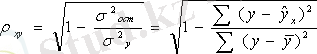
$C:\Users\Zhanar\Desktop\2_clip_image032.gif$

Құрылған модельдің сапасын детерминация коэффициенті арқылы және орташа аппроксимациялық қателік арқылы анықтауға болады
Детерминация коэффициенті - бұл сызықты функцияны таңдап алудың сапасын бағалау үшін қолданылатын сызықты коэффициент. Былай өрнектеледі: 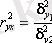$C:\Users\Zhanar\Desktop\2_clip_image034.gif$ мұндағы түсіндірілетін регрессия, 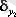$C:\Users\Zhanar\Desktop\2_clip_image040.gif$ шешуші белгінің жалпы жалпы дисперсиясы, ал - 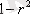$C:\Users\Zhanar\Desktop\2_clip_image042.gif$ модельге кірмейтін фактордың дисперсия бөлігі

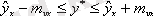Корреляция коэффициентінің мәні -1 $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ r $C:\Users\Zhanar\Desktop\2_clip_image024.gif$ 1 . Регрессия теңдеуі бойынша болжамдық есептеулер нақты болжам болуы керек. Кейде нақты болжам әруақытта дұрыс болмайды. Сондықтан ол стандартты қателікпен толықтырылады, және болжамның интервальдық бағаларымен анықталады. $C:\Users\Zhanar\Desktop\2_clip_image046.gif$ .

Стандартты қателік регрессия коэффициентінің қателігі мен қателігіне байланысты.
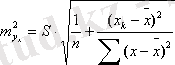$C:\Users\Zhanar\Desktop\2_clip_image050.gif$ -регрессия мәнінің стандартты қателігінің формуласы. Экономикалық құбылыстар арасында сызықты емес қатыстар болса, онда олар сызықты емес функциялармен анықталады. Мысалы, тең қабырғалы гипербола 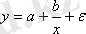$C:\Users\Zhanar\Desktop\2_clip_image008.gif$ , екінші дәрежелі парабола 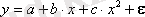$C:\Users\Zhanar\Desktop\2_clip_image054.gif$ т. б

Регрессия коэффициентінің экономикалық түсіндірмесін мысал а рқылы көрсету

Болжам жасау аймақ экономикасындағы мүмкін болатын сандық өзгерістерді ғылыми негіздеуге, аймақ дамуының стратегиялық, ағымдағы және индикативтік жоспарларын құру үшін базаны құруға мүмкіндік береді. Болжамдық бағалау ықтимал түрде болады, себебі онда болжанатын құбылыстардың кездейсоқтық табиғаты сипатталады.

Болжамдар болжанатын объектінің ерекшелігіне байланысты экономикалық, ғылыми-техникалық, демографиялық, әлеуметтік және басқа болады. Пайдаланатын ақпараттың көзі, болжам құрудың механизмі, соңғы нәтижелердің анықтығы бойынша ажыратылатын алдын-ала болжаудың жүзден аса әдістері мен арнайы процедуралары бар.

Экономикалық болжамдау әдістерін екі топқа бөлуге болады. Бірінші топқа - зерттелетін объектінің заңдылықтарын модельдеу және экстрополяцияға негізделетін әдістер жатады; екінші топқа - талданатын құбылысты сараптауға негізделген әдістер жатады.

Елдегі агроөнеркәсіптік өндіріс дамуының аймақтық ерекшеліктерін зерттеу барысында болжамдау әдісін дұрыс қолданылуы өте маңызды болжамдау процесінің дұрыс жүргізілуі өз кезегінде кездесетін экономикалық қиыншылықтыр, әлеуметтік жағдайлар және т. б. маңызды факторларды ескерумен ерекшеленеді. Осыған сәйкес факторлы талдаудың негізгі міндеттері:

- Зерттелетін нәтижелік көрсеткіштерді анықтайтын факторларды жинақтау;

- Факторлар әсерін кешенді және жүйелі түрде зерттеуді қамтамасыз ету мақсатымен факторларды жіктеу және жүйелендіру;

- Факторлар және нәтижелік көрсеткіштер арасындағы байланыс формасын анықтау;

- Нәтижелі және факторлы көрсеткіш арасындағы өзара байланысты модельдеу;

- Факторлар әсерін есептеу және олардың әр қайсысының нәтижелі көрсеткіш көлемінің өзгерісіндегі рөлін бағалау;

- Факторлық модельмен жұмыс.

Кез - келген көрсеткішті талдау үшін факторларды жинақтау - осы салаға байланысты жинақталған теориялық және тәжірибелік білім негізінде жүзеге асырылады. Зерттелетін факторлар саны көп болған сайын талдау нәтижелері дәлірек болады. Сонымен қатар, бұл факторлар кешені олардың өзара әрекеттері есепке алынбай, негізгілері және анықтаушылары бөлініп алынбай механикалық сома ретінде қарастырылса, онда нәтижелері қате болып шығуы мүмкін.

Жоғарыда аталып кеткендей, факторлы талдаудың негізгі міндеттері болып - нәтижелі көрсеткіштер мен факторлар арасындағы өзара байланысты модельдеу табылады модельдеу арқылы зерттеу объектісінің моделін құруға болады. Оны зерттелетін көрсеткіштердің факторларымен өзара байланысын нақты математикалық теңдеулер арқылы көрсетеді.

Факторлық талдауда модельдерде детерминивті және стохастикалық деп бөлуге болады. Экономикалық зерттеулерде стохастикалық байланыстар жиі кездеседі. Стохастикалық (корреляциялық - регрессиялық) байланыс бұл көрсеткіштер арасындағы толық емес, ықтималды байланыс.

2005-2009 жылдар арасындағы белгіленген факторлардың динамикасы келесі 14-кестеде көрсетілген.

Кесте 1

Бастапқы мәліметтер

Жылдар

Ауыл шаруашылығының жалпы өнімі, млн. теңге

Дән,

мың тонна

Ет (сойыс салмағында), мың тонна

Сүт,

мың тонна

Х 1

Х 2

Х 3

Жылдар: 2005

Ауыл шаруашылығының жалпы өнімі, млн. теңге: 45737, 4

Дән,мың тонна: 657

Ет (сойыс салмағында), мың тонна: 42

Сүт,мың тонна: 245, 0

Жылдар: 2006

Ауыл шаруашылығының жалпы өнімі, млн. теңге: 45832, 3

Дән,мың тонна: 429

Ет (сойыс салмағында), мың тонна: 43

Сүт,мың тонна: 253, 0

Жылдар: 2007

Ауыл шаруашылығының жалпы өнімі, млн. теңге: 60331, 9

Дән,мың тонна: 420

Ет (сойыс салмағында), мың тонна: 45

Сүт,мың тонна: 260, 8

Жылдар: 2008

Ауыл шаруашылығының жалпы өнімі, млн. теңге: 63202, 0

Дән,мың тонна: 148

Ет (сойыс салмағында), мың тонна: 46, 6

Сүт,мың тонна: 266, 9

Жылдар: 2009

Ауыл шаруашылығының жалпы өнімі, млн. теңге: 68463, 1

Дән,мың тонна: 553, 3

Ет (сойыс салмағында), мың тонна: 47, 3

Сүт,мың тонна: 269, 2

Бұл кесете нәтижелі және факторлық көрсеткіштер арасындағы байланыстың сипатын және жиілігін белгілеу, сонымен бірге өнім көлемінің таңдалған факторларға тәуелділігін айқындайтын регресся теңдеуін анықтау қажет.

Біріншіден коррелляциялық талдау жүргіземіз. Оның мақсаты - байланыстың сипатын (тура не кері) және байланыстың күшін (байланыс жоқ, әлсіз байланыс, бірқалыпты, байқалатын байланыс, күшті, өте күшті байланыс, толық байланыс) анықтау. Корреляциялық талдау байланыстың сипаты мен анықтық дәрежесі (корреляция коэффициенті) туралы ақпарат береді, ол маңызды факторларды таңдау үшін қажет. Байланыс тығыздығын бағалаудың сандық шарттары келесі кесте 2- де берілген.

Кесте 2

Байланыс тығыздығын бағалаудың сандық шарттары

Корреляция коэффициентінің көлемі, rŷx

Байланыстың бағасы

Корреляция коэффициентінің көлемі, rŷx: Rŷx < 0

Байланыстың бағасы: Кері байланыс

Корреляция коэффициентінің көлемі, rŷx: Rŷx > 0

Байланыстың бағасы: Тура байланыс

Корреляция коэффициентінің көлемі, rŷx: Rŷx < + - 0, 1

Байланыстың бағасы: Байланыс жоқ

Корреляция коэффициентінің көлемі, rŷx: + - 0, 1 < = rŷx < + - 0, 3

Байланыстың бағасы: Әлсіз байланыс

Корреляция коэффициентінің көлемі, rŷx: + - 0, 3 < = rŷx < + - 0, 5

Байланыстың бағасы: Бірқалыпты байланыс

Корреляция коэффициентінің көлемі, rŷx: + - 0, 5 < = rŷx < + - 0, 7

Байланыстың бағасы: Байқалатын байланыс

Корреляция коэффициентінің көлемі, rŷx: + - 0, 7 < = rŷx < + - 0, 9

Байланыстың бағасы: Күшті байланыс

Корреляция коэффициентінің көлемі, rŷx: + - 0, 9 < = rŷx < + - 0, 99

Байланыстың бағасы: Өте күшті байланыс

Корреляция коэффициентінің көлемі, rŷx: + - 0, 99 < = rŷx < + - 0, 1

Байланыстың бағасы: Толық байланыс

Корреляциялық талдауды Exsel арқылы орындау үшін келесі команданы орындаймыз: Сервис → Анализ Данных → Корреляция. Диалогты терезе ашылады. Ол терезеде «Входной диапозон ячеек» деген параметрді толтыру үшін бастапқы мәліметі бар кестені, яғни Кесте - ды ерекшелейміз. «По столбцам» немесе «По строкам» параметрлерінің біріне жалауша орнатамыз. Біздің жағдайда «По столбцам» параметріне жалауша орнатылады.

Егер кестеде тақырып қатары (немесе бағанасы) бар болса «Метки» параметріне жалауша қойып, соңынан «ОК» батырмасын басамыз. Корреляциялық матрица автоматты түрде жаңа параққа шығады. Ол кестеде көрсетілген.

Кесте 3

Корреляциялық талдау

Көрсеткіштер

Х1

Х2

Х3

Көрсеткіштер: У

У: 1

Х1:

Х2:

Х3:

Көрсеткіштер: Х1

У: 0, 323832

Х1: 1

Х2:

Х3:

Көрсеткіштер: Х2

У: -0, 62209

Х1: -0, 37808

Х2: 1

Х3:

Көрсеткіштер: Х3

У: 0, 856295

Х1: -0, 18656

Х2: -0, 31764

Х3: 1

Кесте мәліметтері бойынша, корреляциялық талдаудың нәтижесінде шығатын корреляциялық матрицада айнымалылардың әрбір жұбы үшін корреляция коэффициенті көрсетіледі. Ол байланыстың екі түрінің сипаты мен күшін анықтауға мүмкіндік береді, яғни тәуелді және тәуелсіз айнымалылардың арасындағы байланысты анықтауға көмектеседі. Корреляциялық талдау нәтижесінде Ауыл шаруашылығының жалпы өнімі, млн. теңге (у), Дән, мың тонна (х1) және Ет (сойыс салмағында), мың тонна (х2), Сүт, мың тонна (х3), өте күшті байланыста екенін көреміз.

Регрессиялық талдау жүргізген кезде байланыстың ең нақты өлшемін табуға тырысады, ол у - тің мәнін болжауға мүмкіндік береді. Бұл өлшемді көптік сызықтық регрессиялық байланыстың математикалық моделі түрінде көрсетеді:

у = а b1x1 + b2x2 + b3x3,

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.