Ляпунов тұрақтылығы

Пән: Автоматтандыру, Техника
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министірлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

«Автоматика және элекротехника» кафедрасы

СӨЖ

Тақырыбы: Ляпунов тұрақтылығы

Орындаған: Оразканов Б. Б.

Тобы: АУ-301

Тексерген: Секербаева А. Б.

2015 ж.

Мазмұны:

1. Кіріспе . . . 2

2 . Ляпунов функциясы жəне оның əр уақыттағы туындысы . . . . . . 2

3 . Сызықтық емес жүйелердің тұрақтылығы туралы Ляпунов теоремасы . . . 4

4. Пайдаланылған әдебиеттер . . . 6

Кіріспе

Ляпунов əдісі деп те аталатын Ляпуновтың тікелей əдісін қолданғанда бірінші тəртіп теңдеуі түріндегі автоматты жүйенің дифференциалды теңдеуін қолданамыз. n қатарындағы сызықтық емес жүй үшін бұл теңдеулер мына түрде болады:

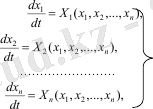(1. 1)

мұнда X1, X2, . . . , Xn функциялары туынды жəне сызықсыздықтың кез-келген түріне ие болады бірақ əрқашан

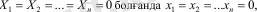шартын қанағаттандырады, себебі орныққан жағдайда барлық өтпелі ауытқулар мен туындылар тең болады. Ары қарай бізге келесі мағлұматтар керек болады.

Ляпунов функциясы жəне оның əр уақыттағы туындысы

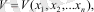
болғанда нөлге айналатын кез келген функцияны Ляпунов

функциясы деп атаймыз, егер онда сол айнымалы ауыспалы процесстердегi ауытқулары x1, x2, . . . , xn шамалар ретiнде алынса

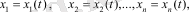
сол жүйе үшiн (1. 1) теңдеулері жазылады.

Ляпуновтың функциясынан туынды (1. 3) əр уақытта

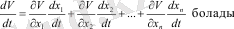
Мұнда таңдалған теңдеулерден 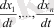мағыналарын қоя отырып,

Ляпуновтың функциясынан əр уақытта келесі түрдегі (1. 1) туындыны аламыз

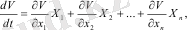
мұнда X1, X2, . . . , Xn - өзiмен x1, x2, . . . , xn ауытқуларынан таңдалған функцияларды ұсынатын теңдеулердiң оң бөлiктерi (1. 1) .

Демек, Ляпунов функциясынан туынды əр уақытта, сонымен қатар өзі сияқты ауытқулардың кейбiр функциясы болып табылады, яғни 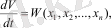жəне де өз қасиетіне (1. 2) сəйкес бұл W функциясы дəл V сияқты 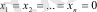болғанда нөлге айналады.

Сондықтан оған бiрдей дəрежеде тұрақтылық жəне жоғары айтылатын V функциясына қатысты түсініктерді қолдануға болады

Бұл жерде мəселе тек теңдеулер туралы ғана болады, оларға t уақыт

нақты түрде кірмейді. Жалпы Ляпунов əдісі t уақыт нақты түрде болғанда да

қолданылуы мүмкін, негізінен ауыспалы коэффиценттері бар теңдеулер үшін.

Осы мəліметтерге сүйене отырып сызықтық емес жүйелердің тұрақтылығы мен тұрақсыздығы туралы Ляпунов теоремасының жалпы

түсініктемесін береміз.

Егер берілген реттеу жүйесінің бастапқы теңдеулері дұрыс болса бұл теоремалар реттеу жүйелерін үлкен жəне кіші ауытқулар кезінде де зерттеуге пайдаланылады. Кез - келген үлкен ауытқу кезінде жүйенің

тұрақтылығы қысқаша жалпы тұрақтылық деп аталады.

Сызықтық емес жүйелердің тұрақтылығы туралы Ляпунов теоремасы

Теорема келесі түрде құрылады: егер п қатарындағы теңдеу жүйесі формасында берілген, уақыт бойынша туындысы W(x1, x2, . . . , xn ) нақты болатын, бірақ V белгісіне карсы W(x1, x2, . . . , xn) туындысы болса ол жүйе тұрақты деп есептеледі. W нақты функциясы кезінде асимптотикалық тұрақтылық пайда болады

Осы теореманың дұрыстығын геомтриялық мысалдармен сипаттайық. Жеңілдік үшін үшінші ретті жүйені алайық (п = 3) . Ол үшін (1. 1) теңдеудің жалпы түрі мынандай болады:

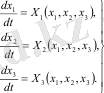
Ляпуновтың тұрақты оң функциясын аламыз

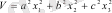
мұнда а, b, с - кез-келген нақты сандар. V мəніне V=0, C1, C2, C3, . . . , өспелі нақты мəндерді береміз, бұл мынаны білдіреді.

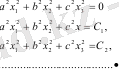
Бұл өрнектің біріншісі ғана x1 = x2 = x3 = 0 нүктесіне сай, ал қалғандары фазалық кеңістіктегі элипсоидтардың бетіне сай болады. Əр алдыңғы элипсоид келесі элипсоидтың (1. 2 сурет) ішінде орналасады. Енді уақыт бойынша Ляпунов функциясынан туынды аламыз. (1. 3) жəне (1. 4) сəйкес

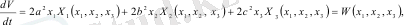
мұнда X1, X2, X3 функциялары реттеу жүйесінің (1. 5) берілген теңдеулерінен алынады.

Егер осындай жолмен алынған W(x1, x2, xs) функциясы теріс нақты, т. б

егер

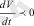
болса 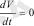(x1=x2=x3=0 бойынша) координаттар басынан басқа

зерттелетін фазалық кеңістіктің барлық нүктелерінде М нүктесі F азаю

жағына қарай жылжиды, яғни элипсоидтарды қиып өтеді (1. 2-сурет) .

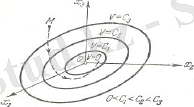
1. 2 - сурет. Фазалық кеңістік

Нəтижесінде уақыт ағымымен М бейнелеуші нүктесі О фазалық кеңістігінің координаттар басына ұмтылады жəне өзі кірген элипсоидтардың сыртына шыға алмайды

Бұл уақыт ағымы бар өтпелі процесстерде барлық x1, x2, x3 ауытқулардың сөнетінін білдіреді. Осылайша осы реттеу жүйесінің тұрақтылығы анықталады. Бұл теореманың үшінші рет үшін дұрыс екенін көрсетеді.

Осыдан теореманың жалпы жағдайда да дұрыс болатыны көрінеді. Пікірлер сол күйде қалады, тек үш теңдеу орнына n теңдеулер қолданылады. Бұрынғыдай Ляпуновтың барлық V (x1, x2, . . . , xn) =C нақты оң

функциясы үшін бірқатар тұйық кеңістіктерді аламыз, бірақ олар енді үш өлшемді фазалық кеңістіктерде болады. Сондықтан 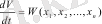туындысы нақты теріс болса n кеңістігіндегі М бейнелеуші нүктесінің траекториясы кез-келген бастапқы шарттарда көерсетілген кеңістіктерді ішінен сыртына қарай қиып өтеді. Бұл жүйенің тұрақты екенін көрсетеді.