Интегро-дифференциалдық теңдеулерді Фредгольм теоремасының үш аналогы негізінде шешу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 46 бет
Таңдаулыға:
Интегро-дифференциалдық теңдеулерді шешудің кейбір әдістері
Мазмұны
КІРІСПЕ
XVIII-XIX ғасырларда физиктер мен математиктер интегралды дифференциалды теңдеулермен шешілетін есептерді зерттеді. Мысалы:
1) серпімді аралық тепе теңдігі бойынша Проктор есебі
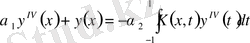 ;
;
2) айналмалы тербеліс бойынша Вольтерр есебі
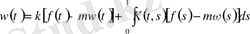 ;
;
3) ұшақ қанатын есептеу Прандтля есебі
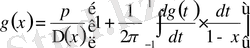 .
.
Интегралды дифференциалды теңдеулер теориясын жасау тарихы 1903 жылы Бурбакидің жұмыстарынан басталды. 1934 жылы А. И. Некрасов [6] интегралды дифференциалды теңдеулерді зерттеу және шешу бойынша маңызды нәтижелерді жариялады. Кейіннен осы жұмыстың идеясын С. Г. Михлин [1], М. Л. Краснов [2], И. Г. Петровский [4] және басқалар дамытты.
Интегралды дифференциалды теңдеулерге белгісіз функциясы және оның туындылары интеграл астына немесе интегралдың сыртына кіретін функционалды теңдеулер жатады. Сондықтан, интегралды теңдеулерге қарағанда оларға белгісіз функцияның туындылары жатады. Интегралды дифференциалды теңдеулер, интегралды сияқты Фредгольм және Вольтерр типті теңдеулерге бөлінеді.
Фредгольм типті сызықты емес интегралды дифференциалды теңдеуге қатысты жалпы есебін келтіреміз:
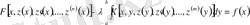 .
.
Жұмыстың мақсаты: Жұмыстың негізгі мақсаты интегралды дифференциалды теңдеулер үшін Фредгольм теоремасын қолданып интегралды теңдеулерге келтіру болып табылады. Интегралдық дифференциалдық теңдеулерді шешуде Фредгольм теоремасының бірінші, екінші, және үшінші аналогтары бойынша қарастыру. Шешілетін интегралдық теңдеудің арнайы түрін шешу, ядро және резольвентаны интегралдау, Коши есебі, Коши специкалық есебі, шеткі есептерімен сыртқы және ішкі дифференциалды операторлардың реттіліктерінің қатынастарына байланысты есептерді шешу және т. с. с.
Зерттеу әдістері: Жұмысты дайындау барысында интегралды дифференциалды теңдеулер үшін Фредгольм теоремасы және кейбір есептеулер қолданылды. Сондай-ақ, А. И. Некрасовтың [6] минорлы қатары есептеулерде қолданылады.
Дипломдық жұмыстың құрылымы: Жұмыстың негізгі бөлімі, үш тараудан және алты парагрофтан құралған.
Бірінші тарауда, Фредгольм теоремасының бірінші аналогын енгізу мәселесі, интегралды теңдеуге келтіру және А. И. Некрасовтың [6] минорлы қатары қарастырылады.
Екінші тарауда, Фредгольм теоремасының екінші аналогын енгізуге арналады. Бұл жерде жоғарғы ретті минорлы қатарлар арасындағы байланыс, сызықтық тәуелсіздік және фундаментальды функциялар жүйесінің шешімдерінің толықтығы қарастырылады.
Үшінші тарауда, Фредгольм теоремасының үшінші аналогы қарастырылады, мұнда екі шешілетін интегралдық теңдеулердің шешімдері арасындағы байланыс және сызықтық интегралдық дифференциалдық теңдеулер қолданылды.
- ФРЕДГОЛЬМ ТЕОРЕМАСЫНЫҢ БІРІНШІ АНАЛОГЫИНТЕГРАЛДЫ ДИФФЕРЕНЦИАЛДЫ ТЕҢДЕУЛЕРДІ
ИНТЕГРАЛДЫ ТЕҢДЕУЛЕРГЕ КЕЛТІРУ
Теңдеуді қарастырайық
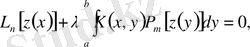 (1. 1. 1)
(1. 1. 1)
мұнда
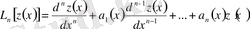
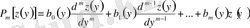
Екі дифференциялдық операторлардың коэффициенттері-үзіліссіз функция-
лар
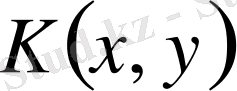 ядросы
ядросы
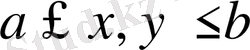 квадратында регулярлы,
квадратында регулярлы,
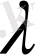 сандық параметр және
сандық параметр және
 .
.
Шешілетін интегралдық теңдеуге келтіру есебін қояйық.
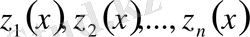 дифференциялдық теңдеулердің фундаментальді шешімінің жүйесі болсын
дифференциялдық теңдеулердің фундаментальді шешімінің жүйесі болсын
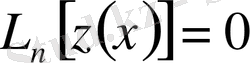 , (1. 1. 2)
, (1. 1. 2)
cонда оның жалпы интегралы
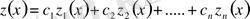 (1. 1. 3)
(1. 1. 3)
түрінде жазылады.
(1. 1. 2) теңдеуді
(1. 1. 4)
деп алайық, мұнда
 әзірше белгісіз функция.
әзірше белгісіз функция.
(1. 1. 4) теңдеудегі
 ті
ті
 белгісіз функция арқылы өрнектеу үшін еркін тұрақтыларды вариациялау әдісін қолданамыз, яғни (1. 1. 4) теңдеудің шешімін
белгісіз функция арқылы өрнектеу үшін еркін тұрақтыларды вариациялау әдісін қолданамыз, яғни (1. 1. 4) теңдеудің шешімін
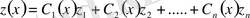
түрінде іздейміз.
Сонда
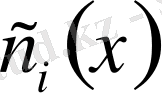 белгісіз жүйеден анықталады
белгісіз жүйеден анықталады
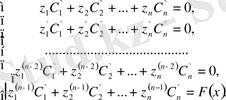 (1. 1. 5)
(1. 1. 5)
Бұл жүйенің бас анықтауышы
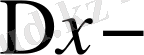 ті (1. 1. 2) теңдеудегі функциясының фундаментальды жүйенің Вронский анықтауышы
ті (1. 1. 2) теңдеудегі функциясының фундаментальды жүйенің Вронский анықтауышы
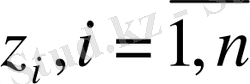 .
.
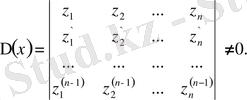 (1. 1. 6)
(1. 1. 6)
Сонда Крамер формуласы бойынша
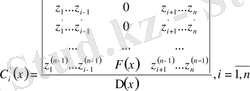
табамыз немесе
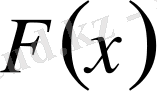 элементінің соңғы қатарына
элементінің соңғы қатарына
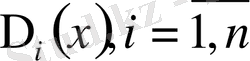 алгебралық толықтауыш арқылы белгілесек
алгебралық толықтауыш арқылы белгілесек
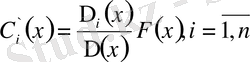 (1. 1. 7)
(1. 1. 7)
аламыз.
(1. 1. 7) өрнекті интегралдасақ
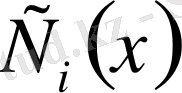 анықтаймы:
анықтаймы:
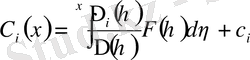 (1. 1. 8)
(1. 1. 8)
және
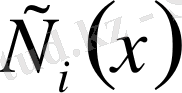
 формуласына қойып, (1. 1. 4) теңдеудің жалпы интегралын
формуласына қойып, (1. 1. 4) теңдеудің жалпы интегралын
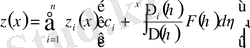 (1. 1. 9)
(1. 1. 9)
Сонымен (1. 1. 9) өрнек (1. 1. 1) интегралдық дифференциялдық теңдеуді қанағаттандыруы үшін
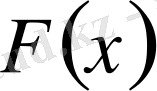 функциясын таңдауды қояйық. Ол үшін (1. 1. 9)
функциясын таңдауды қояйық. Ол үшін (1. 1. 9)
 ті
ті
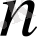 рет дифференциялдап және (1. 1. 5) теңдікті ескеріп,
рет дифференциялдап және (1. 1. 5) теңдікті ескеріп,
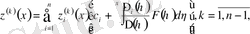
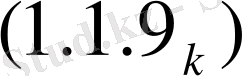
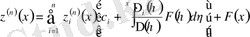
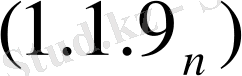
аламыз.
Енді (1. 1. 9) және оның туындылары
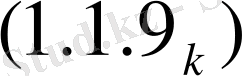 және
және
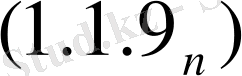 функциялары (1. 1. 1) теңдеуді қанағаттандыру керек екендігін талап етеміз. Олардың өрнектерін (1. 1. 1) теңдеуге қойып шешілетін интегралдық теңдеудің арнайы түріне келтіреміз.
функциялары (1. 1. 1) теңдеуді қанағаттандыру керек екендігін талап етеміз. Олардың өрнектерін (1. 1. 1) теңдеуге қойып шешілетін интегралдық теңдеудің арнайы түріне келтіреміз.
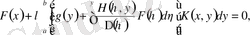 (1. 1. 10)
(1. 1. 10)
мұнда
 белгісіз функция,
белгісіз функция,
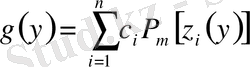 және
және
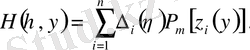
(1. 1. 10) теңдеудің шешімін Нейман қатары түрінде іздейміз
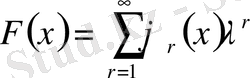 . (1. 1. 11)
. (1. 1. 11)
Егерде (1. 1. 10) теңдеудің шешімін (1. 1. 11) қатар түрінде ұсынылса онда оны (1. 1. 10) теңдеуге қойып және бірдей дәрежелі
 ның коэффициенттерін теңестіріп, бұл қатардың коэффициенттері үшін рекурренті формуласын аламыз:
ның коэффициенттерін теңестіріп, бұл қатардың коэффициенттері үшін рекурренті формуласын аламыз:
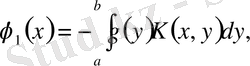
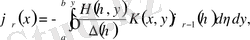
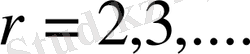
Бұл қатардың келесі (1. 1. 12) шектеулермен жинақтылығын дәлелдейік:
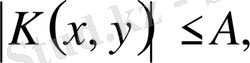
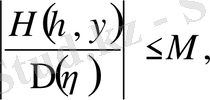
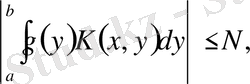
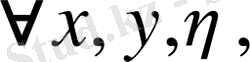
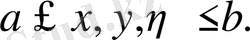

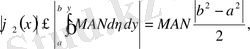
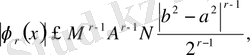
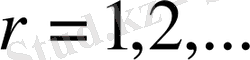 .
.
(1. 1. 11) қатардың оң жағындағы бағалау коэффициенттерінен сандық қатар құрайық
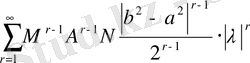 . (1. 1. 13)
. (1. 1. 13)
(1. 1. 13) қатардың мүшелері алымындағы
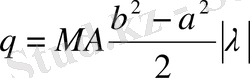 бірге геометриялық прогрессия құрайтындығын және
бірге геометриялық прогрессия құрайтындығын және
 болғанда жинақты болып
болғанда жинақты болып
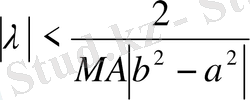 (1. 1. 14)
(1. 1. 14)
орындалатындығын оңай көруге болады.
(1. 1. 13) қатарды құру үшін ол (1. 1. 11) қатар үшін мажорланған болып және Вейершрасс критериі бойынша қатар абсолютті жинақты және
 бірқалыпты болып табылады, мұнда (1. 1. 12) және (1. 1. 14) шектеулер орындалады [2] .
бірқалыпты болып табылады, мұнда (1. 1. 12) және (1. 1. 14) шектеулер орындалады [2] .
Мысал 1. Теңдеуді шешеміз
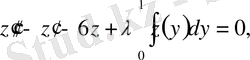
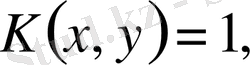
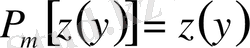 .
.
(1. 1. 2) теңдеу
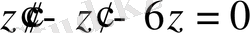 болады, оған сәйкесті сипаттаушы теңдеу
болады, оған сәйкесті сипаттаушы теңдеу
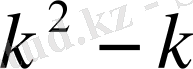
 , ал түбірлері
, ал түбірлері
 ,
,
 болады және бұларға сәйкесті (1. 1. 2) теңдеудің сызықтық тәуелсіз шешімдері
болады және бұларға сәйкесті (1. 1. 2) теңдеудің сызықтық тәуелсіз шешімдері
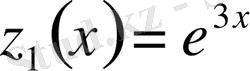 ,
,
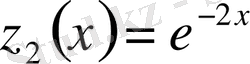 болып, жалпы шешім ретінде
болып, жалпы шешім ретінде
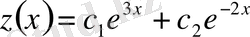 жазуға болады.
жазуға болады.
(1. 1. 4) теңдеудің шешімін табу үшін еркін тұрақтыларды вариациялау әдісін қолданамыз
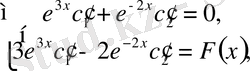 бұдан
бұдан
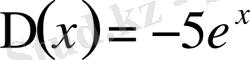 ,
,
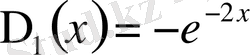 ,
,
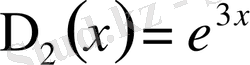 ,
,
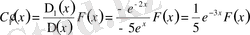 ,
,
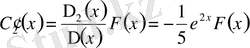 ,
,
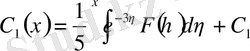 ,
,
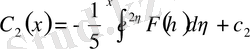 .
.
Бұдан әрі
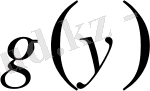 және
және
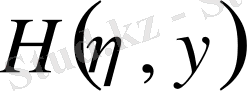 функцияларын (1. 1. 10) теңдеудегі сәйкесті белгілеулермен құрайық
функцияларын (1. 1. 10) теңдеудегі сәйкесті белгілеулермен құрайық
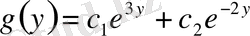 ,
,
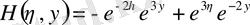 .
.
(1. 1. 1) теңдеудің шешімін белгісіз
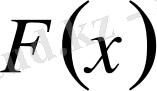 функциясы арқылы (1. 1. 9) формула бойынша жазылады:
функциясы арқылы (1. 1. 9) формула бойынша жазылады:
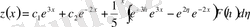 ,
,
ал оның (1. 1. 10) шешілетін теңдеуі мына түрде болады
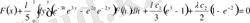 .
.
Шешімді (1. 1. 11) қатар түріндегі шешілетін теңдеуге қойсақ, осы қатардың коэффициентін анықтаймыз
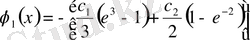 ,
,
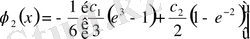 , . . . ,
, . . . ,
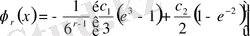 , . . . , қолданып (1. 1. 10) теңдеудің шешімін табамыз
, . . . , қолданып (1. 1. 10) теңдеудің шешімін табамыз
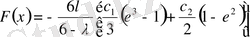 .
.
Бұл шешімді (1. 1. 9) формулаға қойсақ, берілген интегралдық дифференциялдық теңдеудің шешімін
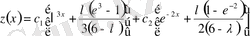
түрінде аламыз.
(1. 1. 11) қатардың коэффициенттерін түрлендірейік, ол үшін
 өрнегін
өрнегін
 ке қойып, алдын-ала
ке қойып, алдын-ала
 өрнегін
өрнегін
 және
және
 алмастырамыз, сонда интегралдау ретінің өзгеруінен
алмастырамыз, сонда интегралдау ретінің өзгеруінен
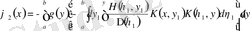 . (1. 1. 15)
. (1. 1. 15)
аламыз.
Алғашқы берілген ядроны бірінші үшін
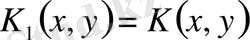 ,
,
ал квадратты жақшадағы итерацияланған ядроны екінші үшін қолдансақ
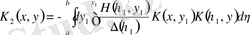 ,
,
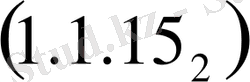
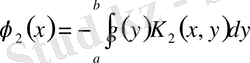 аламыз. Одан соң
аламыз. Одан соң
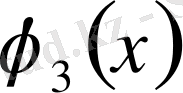 коэффициенттерін түрлендіреміз.
коэффициенттерін түрлендіреміз.
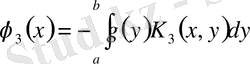 ,
,
мұнда
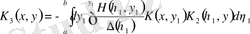 ,
,
дәл осындай
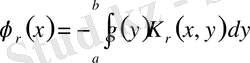 ,
,
мұнда
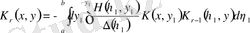 ,
,
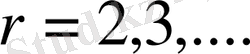 .
.
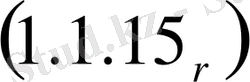
(1. 1. 11) қатардағы
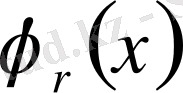 коэффициентінің жаңа өрнегіне қойып және осы қатардың бірқалыпты жинақтылығынан бір интеграл астындағы барлық қосылғыштарды топтастырып
коэффициентінің жаңа өрнегіне қойып және осы қатардың бірқалыпты жинақтылығынан бір интеграл астындағы барлық қосылғыштарды топтастырып
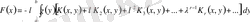 .
.
табамыз.
Квадратты жақшадағы қатарды резольвента деп және оны
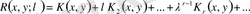 . (1. 1. 16)
. (1. 1. 16)
белгілейміз.
Сонда шешілетін теңдеудің шешімі резольвента арқылы
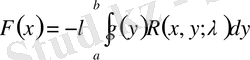 . (1. 1. 17)
. (1. 1. 17)
түрінде жазылады [4] .
Резольвентаның бірқалыпты және абсолютті жинақтылығын аналогиялық түрде (1. 1. 11) қатардағы сол шектеулермен жасалғандай дәлелдеу қиын емес.
Егерде
 коэффициенттерін түрлендіру үшін интегралды басқа ретпен алмастыруды қолдансақ, онда итерацияланған ядро үшін басқа формуланы аламыз
коэффициенттерін түрлендіру үшін интегралды басқа ретпен алмастыруды қолдансақ, онда итерацияланған ядро үшін басқа формуланы аламыз
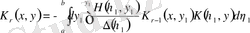 ,
,
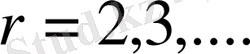 , (1. 1. 18)
, (1. 1. 18)
Интегралдық теңдеудің резольвентасы тағы да екеуін құруға болады. (1. 1. 16) резольвента қатарына итериацияланған ядро мәнін қоюға болады
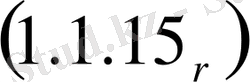 ,
,
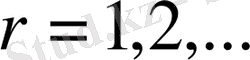 .
.
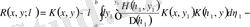
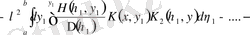
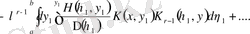
Резольвента үшін өрнектің бірқалыпты жинақтылығынан қайта жазуға болады
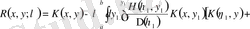
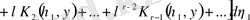 ,
,
Бұл жерден квадраттық жақшадағы тағы да резольвента екенін көреміз
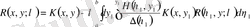 . (1. 1. 19)
. (1. 1. 19)
Егерде (1. 1. 16) резольвента қатарына (1. 1. 18) итериацияланған өрнекті қойсақ, онда қайта есептеп келесі резольвента теңдеуін аламыз
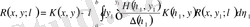 . (1. 1. 20)
. (1. 1. 20)
1. 2 СИПАТТАУЫШ КӨПМҮШЕЛІК ЖӘНЕ А. И. НЕКРАСОВТЫҢ
МИНОРЛЫ ҚАТАРЫ
(1. 1. 10) шешілетін теңдеуді шешуге Нейман қатарын қолданып (1. 1. 14)
 шектеулерін аламыз.
шектеулерін аламыз.
Бұдан әрі (1. 1. 10) теңдеуді
 параметрге қатаң шектеулерсіз шешеміз. Ол үшін жаңа белгісіз функция енгіземіз
параметрге қатаң шектеулерсіз шешеміз. Ол үшін жаңа белгісіз функция енгіземіз
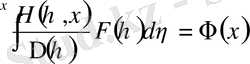 (1. 2. 21)
(1. 2. 21)
.
және (1. 1. 10) теңдеудегі
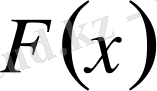 ті (1. 2. 21) теңдікке қойып,
ті (1. 2. 21) теңдікке қойып,

аламыз, бұл жерде белгісіз өрнектер үшін белгілеулер енгізіп, Фредгольмнің интегралдық теңдеуіне келеміз
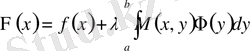 , (1. 2. 22)
, (1. 2. 22)
мұнда
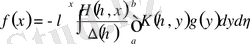 ,
,
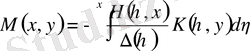 .
.
(1. 2. 22) теңдеуге Фредгольм теоремасын
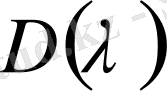 сипаттауыш көпмүшелікке [1] сәйкесті қолданамыз
сипаттауыш көпмүшелікке [1] сәйкесті қолданамыз
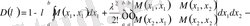
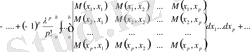
және содан соң (1. 2. 22) теңдеудегі
 ядроны
ядроны
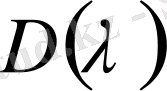 -ға қойып, анықтауышты түрлендіріп, (1. 1. 1) теңдеу үшін сипаттауыш көпмүшелікті аламыз
-ға қойып, анықтауышты түрлендіріп, (1. 1. 1) теңдеу үшін сипаттауыш көпмүшелікті аламыз
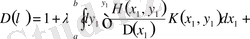
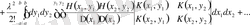
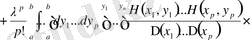
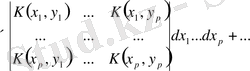 . (1. 2. 23)
. (1. 2. 23)
(1. 1. 10) теңдеуді эквиваленттілігін және (1. 2. 22) теңдеудегі сипаттауыш сандарды сәйкес мүмкіндігін күтуге болады. Белгілеулер
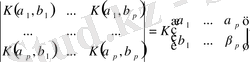
қайта жазып
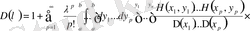
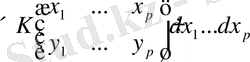 . (1. 1. 24)
. (1. 1. 24)
(1. 1. 10) теңдеудің шешіміне (1. 1. 17) түріне қайта ораламыз
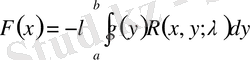 .
.
Резольвентаны
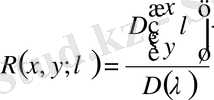 түрінде іздейміз, мұнда
түрінде іздейміз, мұнда
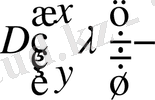 әзірше
әзірше
белгісіз функция. Сонда (1. 1. 10) теңдеудің шешімі мына түрге келеді
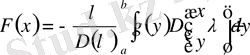 . (1. 2. 25)
. (1. 2. 25)
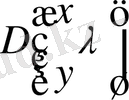 анықтау үшін (1. 1. 19) резольвента теңдеуін қолданып интегралдық теңдеуді аламыз
анықтау үшін (1. 1. 19) резольвента теңдеуін қолданып интегралдық теңдеуді аламыз
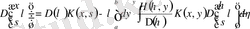 . (1. 2. 26)
. (1. 2. 26)
Бұл функцияны қатардың көмегімен аламыз
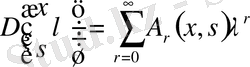 , (1. 2. 27)
, (1. 2. 27)
оны (1. 2. 26) теңдікке қойып, бірдей дәрежелі коэффициенттерін теңестіріп
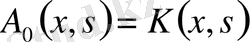 ,
,
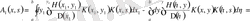
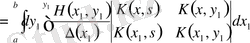 .
.
Аналогиялық түрде
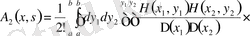
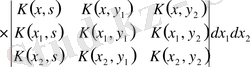 .
.
. . .
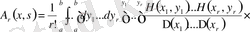
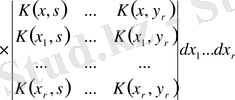
. . .
(1. 1. 27) қатарға
 табылған өрнекті қойып, А. И. Некрасовтың [6] минорлы қатарын -Фредгольмның минорлы қатарына ұқсастығын аламыз
табылған өрнекті қойып, А. И. Некрасовтың [6] минорлы қатарын -Фредгольмның минорлы қатарына ұқсастығын аламыз
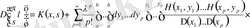
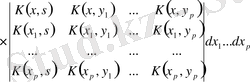 . (1. 2. 28)
. (1. 2. 28)
(1. 1. 24) формулаға белгілеулерді қолданып
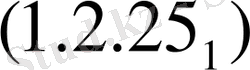 қатар қайта жазылады
қатар қайта жазылады
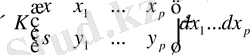 . (1. 1. 29)
. (1. 1. 29)
 қатарын жинақтылыққа зерттейміз(
қатарын жинақтылыққа зерттейміз(
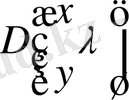 қатары аналогиялық түрде зерттеледі) .
қатары аналогиялық түрде зерттеледі) .
 қатарының коэффициенттері үшін (1. 2. 23) белгілеулер енгіземіз
қатарының коэффициенттері үшін (1. 2. 23) белгілеулер енгіземіз
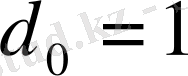 ,
,
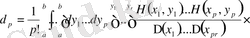
 ,
,
мұнда
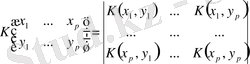 ,
,
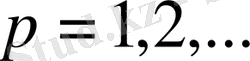 .
.
сонда (1. 2. 21) қатар
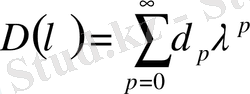 . (1. 1. 30)
. (1. 1. 30)
түріне келеді
(1. 1. 30) қатардың жинақтылыққа дәлелдеу үшін Адамара теңсіздігін еске түсіреміз. Егерде
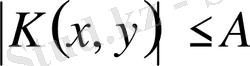
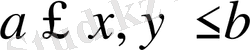 болғанда, онда
болғанда, онда
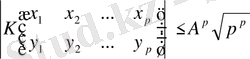 ;
;
және
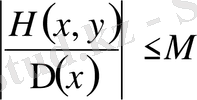 болсын, сонда
болсын, сонда
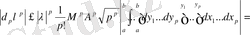
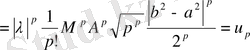 .
.
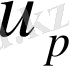 бағалауынан (1. 1. 23) қатар мүшелерінен
бағалауынан (1. 1. 23) қатар мүшелерінен
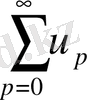 оң сандық қатарын құрамыз, жинақтылыққа Даламбер белгісін пайдаланып дәлелдейміз
оң сандық қатарын құрамыз, жинақтылыққа Даламбер белгісін пайдаланып дәлелдейміз
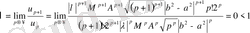 ,
,
сондықтан
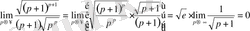 .
.
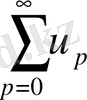 қатары құру бойынша (1. 1. 30) қатар үшін мажорланған болады және шындығында (1. 1. 30) қатар Вейершрасс критерии бойынша
қатары құру бойынша (1. 1. 30) қатар үшін мажорланған болады және шындығында (1. 1. 30) қатар Вейершрасс критерии бойынша
 барлық мәнінде бірқалыпты және абсолютті жинақталады.
барлық мәнінде бірқалыпты және абсолютті жинақталады.
Бәрінен бұрын Фредгольм теоремасының бірінші аналогын тұжырымдау үшін, алдымен (1. 2. 25) формуладағы
 функциясы (1. 1. 10) теңдеуді көз жеткіземіз. (1. 2. 25) формуладағы
функциясы (1. 1. 10) теңдеуді көз жеткіземіз. (1. 2. 25) формуладағы
 функциясының мәнін (1. 1. 10) теңдеуге қоямыз,
функциясының мәнін (1. 1. 10) теңдеуге қоямыз,
 қысқартамыз, айнымалылардың атын өзгертеміз, жалпы
қысқартамыз, айнымалылардың атын өзгертеміз, жалпы
 көбейткішті шығарып, бір жалпы интеграл астына топтастырамыз. Нәтижесінде бірінші резольвента теңдеуіне келеміз
көбейткішті шығарып, бір жалпы интеграл астына топтастырамыз. Нәтижесінде бірінші резольвента теңдеуіне келеміз
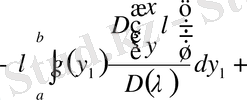
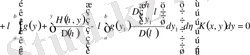 ,
,
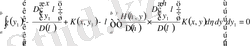 ,
,
бұдан, өйткені
 , жалпы айтқанда
, жалпы айтқанда
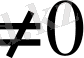 , онда
, онда
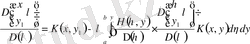 ,
,
яғни
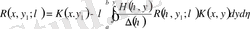 .
.
Содан соң (1. 2. 25) формадағы (1. 1. 10) теңдеудің шешімінің жалғыздығын дәлелдейміз.
Дәлелдеуді кері жору әдісімен жүргіземіз. (1. 1. 10) теңдеуді басқа
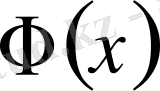 шешімі болсын, сонда
шешімі болсын, сонда
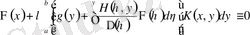 . (1. 2. 31)
. (1. 2. 31)
Бұл тепе-теңдікте
 ты
ты
 ға алмастырамыз, оны
ға алмастырамыз, оны
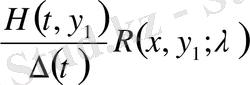
көбейтіп және интегралдаймыз.
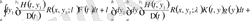
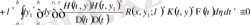 .
.
«*» белгіленген өрнектер:
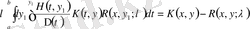 ,
,
екінші интегралдық теңдеудің резольвентасы
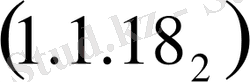 , оны соңғы қосылғышқа қойып интегралдардың қосындысына тіркеп жазамыз
, оны соңғы қосылғышқа қойып интегралдардың қосындысына тіркеп жазамыз
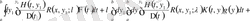
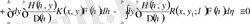 ;
;
сонда бірінші және соңғы қосылғыштар жойылады.
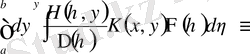
(1. 2. 32)
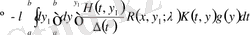 .
.
(1. 2. 32) -ні (1. 2. 31) теңдеуге қойсақ интегралдар айырмасын жазып
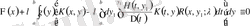 .
.
Демек, квадратты жақшадағы резольвента болса ((1. 1. 19) сәйкесті) онда
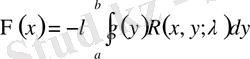 яғни
яғни
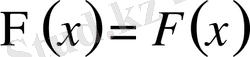 . Жалғыздығы дәлелденді.
. Жалғыздығы дәлелденді.
Фредгольм теоремасының бірінші аналогын тұжырымдайық.
Егерде
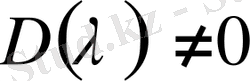 , (1. 1. 10) шешілетін интегралдық теңдеудің (1. 2. 25) формуламен анықталатын жалғыз шешімі бар
, (1. 1. 10) шешілетін интегралдық теңдеудің (1. 2. 25) формуламен анықталатын жалғыз шешімі бар
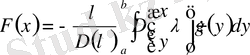 ,
,
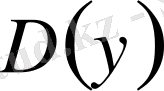 және
және
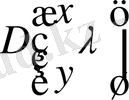
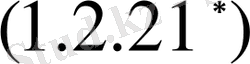 және
және
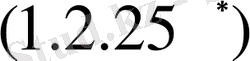 қатарларда
қатарларда
 барлық мәнінде абсолютті және бірқалыпты жинақты.
барлық мәнінде абсолютті және бірқалыпты жинақты.
Анықтама.
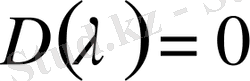 болғандағы
болғандағы
 мәнін
мәнін
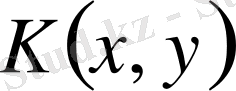 және
және
 ядроларының сипаттаушы немесе фундаментальды саны деп атаймыз [7] .
ядроларының сипаттаушы немесе фундаментальды саны деп атаймыз [7] .
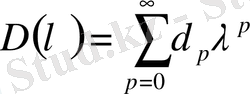 ,
,
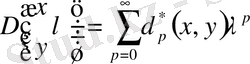
(1. 2. 23) -дегі қосылғыштарды (1. 2. 30) -ғы мен (1. 1. 28) формуланы (1. 1. 29) мен салыстырсақ
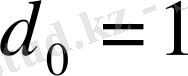 ,
,
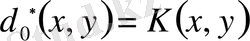 екендігін келесі формуладан көреміз
екендігін келесі формуладан көреміз
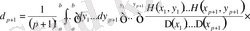
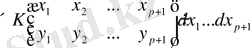 , (1. 2. 33)
, (1. 2. 33)
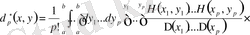
 . (1. 2. 34)
. (1. 2. 34)
(1. 2. 34) теңдікті
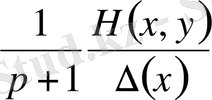 көбейтіп
көбейтіп
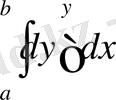 бойынша интегралдаймыз:
бойынша интегралдаймыз:
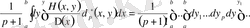
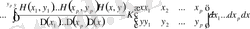 .
.
Соңғы теңдіктің оң жағын
 ті
ті
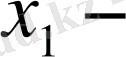 ге,
ге,
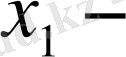 ді
ді
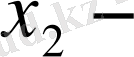 ге, . . . ,
ге, . . . ,
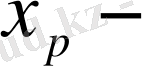
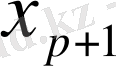 және
және
 ге,
ге,
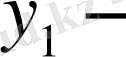 ді
ді
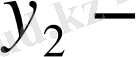 ге, . . . ,
ге, . . . ,
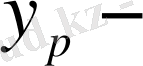
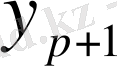 алмастырсақ
алмастырсақ
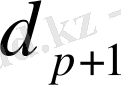 коэффициенттерін аламыз, яғни
коэффициенттерін аламыз, яғни
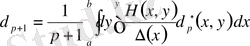 . (1. 1. 35)
. (1. 1. 35)
(1. 1. 35)
 деп алсақ,
деп алсақ,
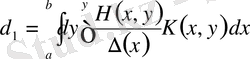
табамыз.
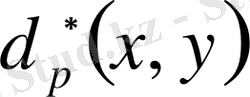 коэффициенттерін анықтау үшін (1. 2. 26) интегралдық теңдеуді
коэффициенттерін анықтау үшін (1. 2. 26) интегралдық теңдеуді
 үшін пайдаланамыз.
үшін пайдаланамыз.
(1. 2. 26) теңдікке (1. 1. 29) қатарды қоямыз
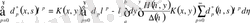 ,
,
 бірдей коэффициенттерін теңестіріп
бірдей коэффициенттерін теңестіріп
 ті
ті
 ке және
ке және
 ті
ті
 ге ауыстырып,
ге ауыстырып,
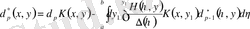 . (1. 1. 36)
. (1. 1. 36)
Енді,
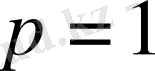 деп (1. 1. 36) қойып,
деп (1. 1. 36) қойып,
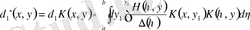
анықтаймыз, бұдан әрі (1. 2. 35) және (1. 2. 36) рекурренттік формуланы қолданамыз.
Ескерту 1. Егерде
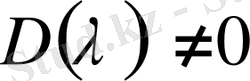 болғанда, яғни
болғанда, яғни
 сипаттауыш сан болмаса, ал
сипаттауыш сан болмаса, ал
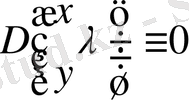 болса (1. 1. 10) шешілетін интегралдық теңдеу тек қана нөлдік шешімге ие болады, және (1. 1. 1) интегралдық дифференциалдық теңдеудің шешімі дифференциалдық теңдеудің шешімдері мен дәлелге дәл келеді.
болса (1. 1. 10) шешілетін интегралдық теңдеу тек қана нөлдік шешімге ие болады, және (1. 1. 1) интегралдық дифференциалдық теңдеудің шешімі дифференциалдық теңдеудің шешімдері мен дәлелге дәл келеді.
 , яғни
, яғни
 .
.
Ескерту 2. Егерде
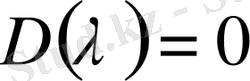 ,
,
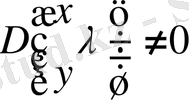 болса, онда шешілетін (1. 1. 10) интегралдық теңдеудің шексіз көп шешімі бар және ол сәйкесінше (1. 1. 1) интегралдық дифференциалдық теңдеудің шексіз шешімдері болады.
болса, онда шешілетін (1. 1. 10) интегралдық теңдеудің шексіз көп шешімі бар және ол сәйкесінше (1. 1. 1) интегралдық дифференциалдық теңдеудің шексіз шешімдері болады.
Ескерту 3.
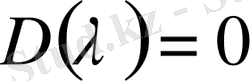 және
және
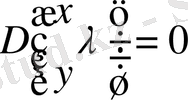 жағдайын ерекше қарауға болады.
жағдайын ерекше қарауға болады.
Мысал 2.
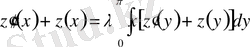 .
.
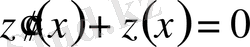 ,
,
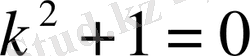 ,
,
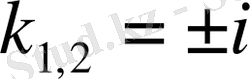 ,
,
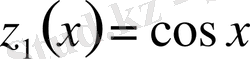 ,
,
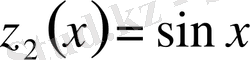 ,
,
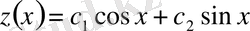 ,
,
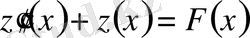 ,
,
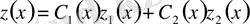 .
.
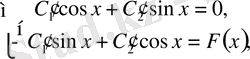
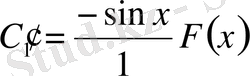 ,
,
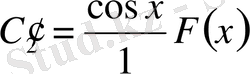
(1. 1. 7) және (1. 1. 10) белгілеулерге сәйкес табамыз
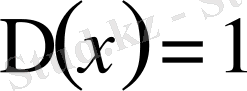 ,
,
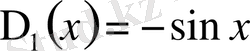 ,
,
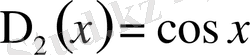 ,
,
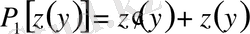 ,
,
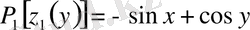 ,
,
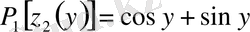 ,
,
 ,
,
 .
.
(1. 1. 35) және (1. 1. 36) рекуррентті формулаларды пайдаланып (1. 2. 30) және(1. 2. 29) қатардың коэффициенттерін табамыз
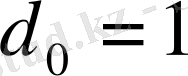 ,
,
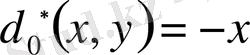 ,
,
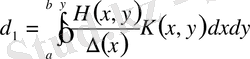 ,
,
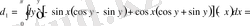
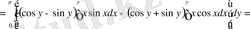
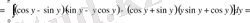

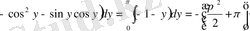 ,
,
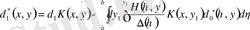 ,
,
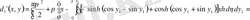

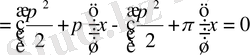 ,
,
сонымен,
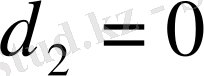 ,
,
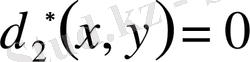 және т. б.
және т. б.
(1. 2. 30) және (1. 2. 29) формула бойынша
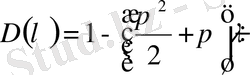 ,
,
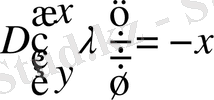 .
.
табамыз.
Сонда (1. 1. 11) және (1. 2. 25) формулаға сәйкесінше алдымен
 ті
ті
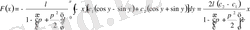
содан соң (1. 1. 9) формула бойынша
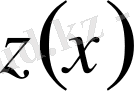 анықтаймыз
анықтаймыз
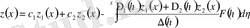 ,
,
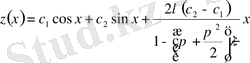 ,
,
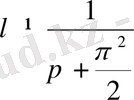 .
.
(1. 1. 1) интегралдық дифференциалдық теңдеуді бастапқы шарттарымен бастапқы есебін қарастырамыз
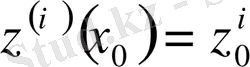 ,
,
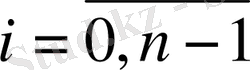 және
және
 .
.
Бастапқы шартты ескере отырып, (1. 1. 9) формуладан (1. 1. 1) теңдеудің шешімін
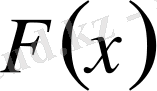 белгісіз функция арқылы қайта жазуымызға болады
белгісіз функция арқылы қайта жазуымызға болады
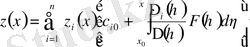 .
.
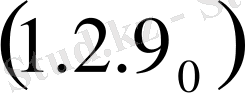
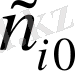 тұрақтының мәні бұл этапта бастапқы есептің шешімін анықтауға болады.
тұрақтының мәні бұл этапта бастапқы есептің шешімін анықтауға болады.
 деп алсақ
деп алсақ
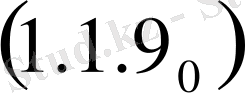 формуладан
формуладан
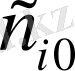 қатысты сызықты алгебралық жүйені аламыз
қатысты сызықты алгебралық жүйені аламыз
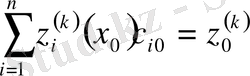 ,
,
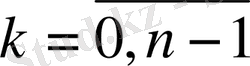 ,
,
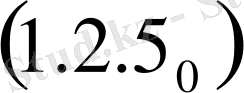
бұл әрқашан шешімі бар, демек бұл жүйенің бас анықтауышы
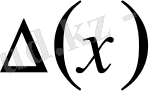 Вронский анықтауышының мәні бар
Вронский анықтауышының мәні бар
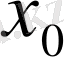 нүктесіндегі
нүктесіндегі
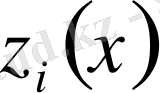 ,
,
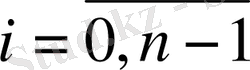 фундаментальды функцияның жүйесі болады
фундаментальды функцияның жүйесі болады
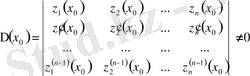
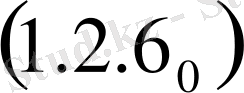
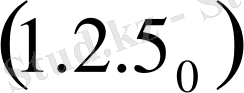 жүйенің
жүйенің
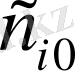 тұрақтының мәнін есептеп және оларды (1. 1. 10) теңдеудегі
тұрақтының мәнін есептеп және оларды (1. 1. 10) теңдеудегі
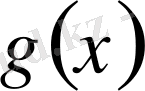 өрнегіне қойсақ, шешілетін интегралдық теңдеудің арнайы түріне келеміз
өрнегіне қойсақ, шешілетін интегралдық теңдеудің арнайы түріне келеміз
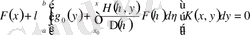 ,
,
мұнда
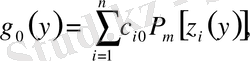
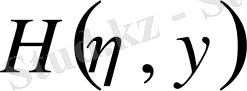 және
және
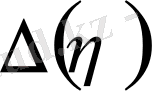 (1. 1. 10) фолмуладағыдай.
(1. 1. 10) фолмуладағыдай.
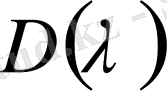 сипаттауыш көпмүшелігін және алғашқы
сипаттауыш көпмүшелігін және алғашқы
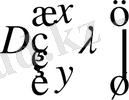 минорлы қатарын табу үшін (1. 1. 10) теңдеуді шешуде бастапқы шарттарды ескере отырып
минорлы қатарын табу үшін (1. 1. 10) теңдеуді шешуде бастапқы шарттарды ескере отырып
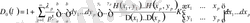 ,
,
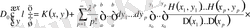
 . (1. 2. 37)
. (1. 2. 37)
Берілген бастапқы шарттармен (1. 1. 1) және (1. 1. 10) теңдеуді шешімдерін
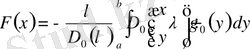 ,
,
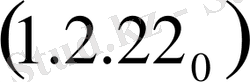
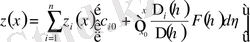
формула бойынша табамыз [5] .
Мысал 3. Коши есебінің шешімдерін және сипаттауыш сандарды анықтау.
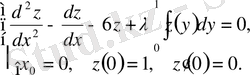
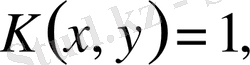
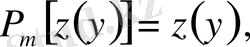
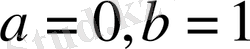 .
.
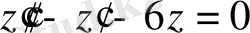 ,
,
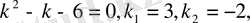
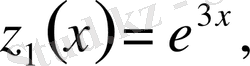
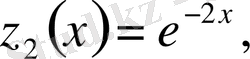
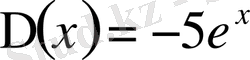 ,
,
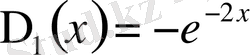 ,
,
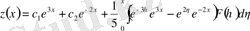 .
.
Бұл жерде 1-ші мысалдағы есептеу нәтижесі қолданылады. Бұдан әрі
 деп алып,
деп алып,
 және
және
 тұрақтыларын тауып
тұрақтыларын тауып
 жүйені жазсақ
жүйені жазсақ
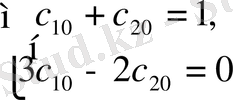 , бұдан
, бұдан
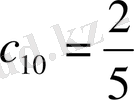 ,
,
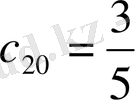 және
және
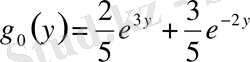 ,
,
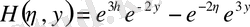 .
.
 шешілетін теңдеу
шешілетін теңдеу
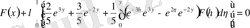
жазылады.
Енді
 және
және
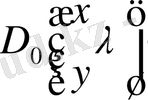 мәндерін (1. 2. 29) және (1. 2. 37) формуласы бойынша табамыз. Сонда берілген екінші және жоғарғы ретті анықтауыштары нөлге тең болса, онда
мәндерін (1. 2. 29) және (1. 2. 37) формуласы бойынша табамыз. Сонда берілген екінші және жоғарғы ретті анықтауыштары нөлге тең болса, онда
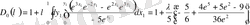 ,
,
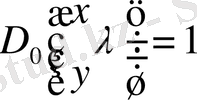 .
.
 және
және
 формуласы бойынша
формуласы бойынша
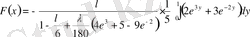 ,
,
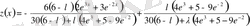 .
.
табамыз.
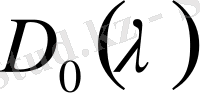 нөлге теңестіріп
нөлге теңестіріп
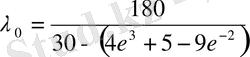
сипаттауыш мәнін табамыз.
2 ФРЕДГОЛЬМ ТЕОРЕМАСЫНЫҢ ЕКІНШІ АНАЛОГЫ
2. 1 ЖОҒАРҒЫ РЕТТІ МИНОРЛЫ ҚАТАРЛАР
Келесі қатарларды жоғарғы ретті минорлы қатар деп атаймыз
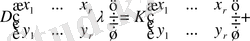
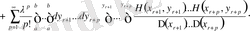
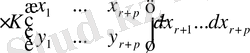 ,
,
 . (2. 1. 1)
. (2. 1. 1)
Жоғарғы ретті минорлы қатарын келесі шектеулермен
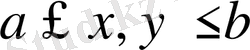 ,
,
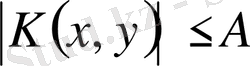 ,
,
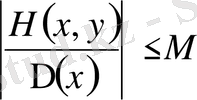 жинақтайық. Сонда Адамар теңсіздігімен сәйкесті
жинақтайық. Сонда Адамар теңсіздігімен сәйкесті
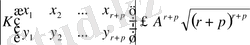 ,
,
(2. 1. 1) қатардың мүшелері үшін шектеулерді аламыз
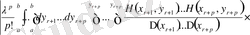
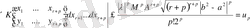 .
.
 қатары Даламбер белгісі бойынша, мұнда
қатары Даламбер белгісі бойынша, мұнда
 , сонымен
, сонымен
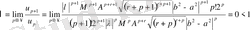
жинақталады.
Бұл шек бірінші тарауда (1. 2. 29)
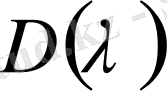 қатарының жинақтылыққа зерттеу барысында қарастырылып қойылған. Сондықтан (2. 1. 1) қатары Вейерштрасс критерии бойынша бірқалыпты және абсолютті жинақталады.
қатарының жинақтылыққа зерттеу барысында қарастырылып қойылған. Сондықтан (2. 1. 1) қатары Вейерштрасс критерии бойынша бірқалыпты және абсолютті жинақталады.
Минорлы қатарлар арасындағы оның құрамына кіретін анықтауыштарды қатар және баған элементтеріне жіктеу тәуелділігін алайық. (1. 2. 28) формуладағы
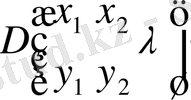 екінші ретті минорлы қатарынан бастайық.
екінші ретті минорлы қатарынан бастайық.
 үшін оның анықтауышын бірінші қатардың элементтеріне жіктейміз:
үшін оның анықтауышын бірінші қатардың элементтеріне жіктейміз:
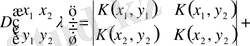
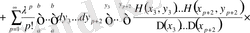
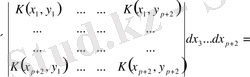
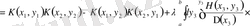
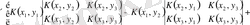
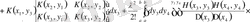
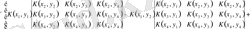
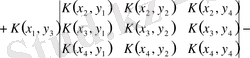
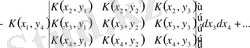 .
.
 және
және
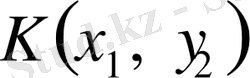 көбейткіштері бар мүшелерін топтап және ортақ көбейткішті жақша сыртына шығарып, жақша ішіне сәйкесті
көбейткіштері бар мүшелерін топтап және ортақ көбейткішті жақша сыртына шығарып, жақша ішіне сәйкесті
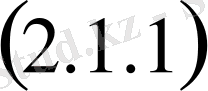 өрнекті алып,
өрнекті алып,
 және
және
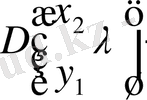 жіктеуін аламыз:
жіктеуін аламыз:
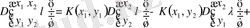
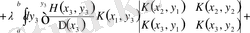
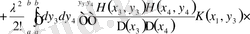
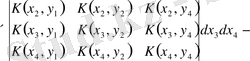
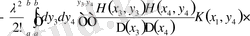
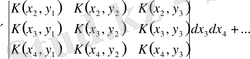
Симметриялық жазба үшін анықтауыштар қатарын алмастырып, содан соң
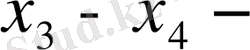 ке,
ке,
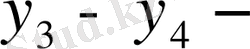 ке және қарама-қарсы
ке және қарама-қарсы
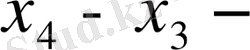 ке және
ке және
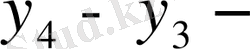 ке және т. б. ауыстырамыз
ке және т. б. ауыстырамыз
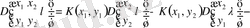
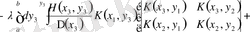
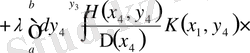
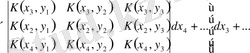
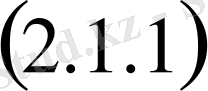 формуладағы тік жақшадағы көрсеткіш
формуладағы тік жақшадағы көрсеткіш
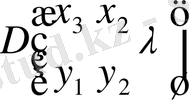 фредгольмның минорлы қатарынан екенін көреміз.
фредгольмның минорлы қатарынан екенін көреміз.
Мұндағы
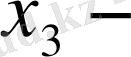 ті
ті
 ,
,
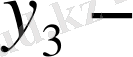 ті
ті
 ке ауыстырып, .
ке ауыстырып, .
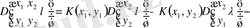
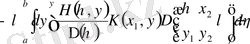 . (2. 1. 2)
. (2. 1. 2)
аламыз.
Бесінші минорды үшінші қатардағы элементтен (жекеше түрде) (1. 2. 29) түсінігін пайдаланып, ажыратып аламыз. Сонда бұл (2. 1. 1) қатар былай жазылады
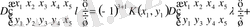
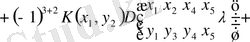
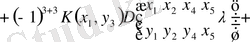
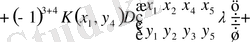
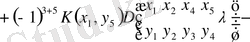
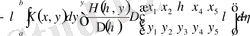
немесе
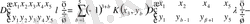
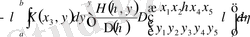 . (2. 1. 3)
. (2. 1. 3)
 ның қатар бойынша
ның қатар бойынша
 минорға жіктеу үшін формуланы аламыз
минорға жіктеу үшін формуланы аламыз
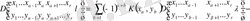
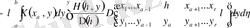 . (2. 1. 4)
. (2. 1. 4)
Енді аналогиялық түрде
 ны баған бойынша
ны баған бойынша
 минорға жіктеу формуласын алуға болады
минорға жіктеу формуласын алуға болады
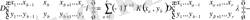
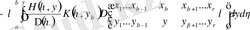 . (2. 1. 5)
. (2. 1. 5)
(1. 1. 10) біртекті емес теңдеудің арнайы түріне сәйкесті біртекті интегралдық теңдеуді жазамыз
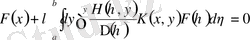 . (2. 1. 6)
. (2. 1. 6)
(2. 1. 6) теңдеудің фундаментальдық функциясын табу үшін бізге
 туындысы қажет болып, оларды табамыз
туындысы қажет болып, оларды табамыз
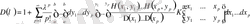 ,
,
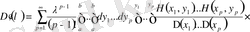
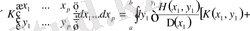
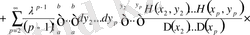
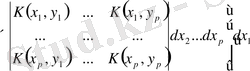 .
.
Квадратты жақшалы (2. 1. 1) формуламен сәйкес келетін
 аламыз және сонымен
аламыз және сонымен
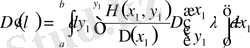 . (2. 1. 7)
. (2. 1. 7)
Аналогиялық түрде
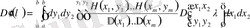 , (2. 1. 8)
, (2. 1. 8)
. . .
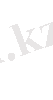
 (2. 1. 9)
(2. 1. 9)
табамыз.

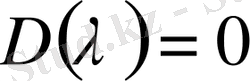 сипаттауыш теңдеудің
сипаттауыш теңдеудің
 еселі түбірі болсын, сонда
еселі түбірі болсын, сонда
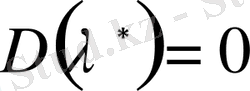 ,
,
 , . . .
, . . .
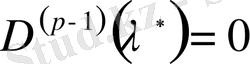 , ал
, ал
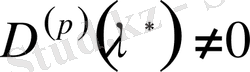 тең. (2. 1. 9) формуладағы
тең. (2. 1. 9) формуладағы
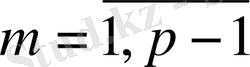 деп алсақ, сонда
деп алсақ, сонда
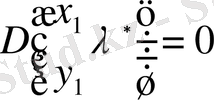 ,
,
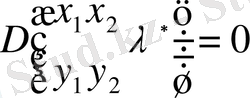 , . . . ,
, . . . ,
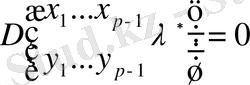 ,
,
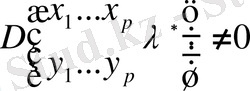 .
.
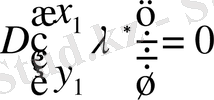 ,
,
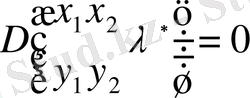 , . . . ,
, . . . ,
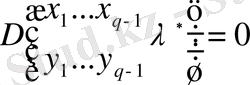 ,
,
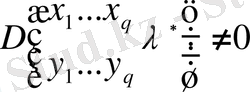 осындай формуладан керісінше
осындай формуладан керісінше
 ,
,
 , . . . ,
, . . . ,
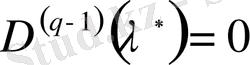 , ал
, ал
 екендігін көру қиын емес, яғни
екендігін көру қиын емес, яғни
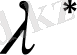 ,
,
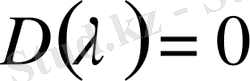 теңдеудің
теңдеудің
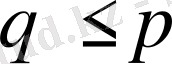 еселі түбірі болып табылады [2-3] .
еселі түбірі болып табылады [2-3] .
Анықтама. Сипаттауыш санның рангі деп жоғарғы ретті минордың бірінші реті нөлге тепе-тең емес.
Жоғарыда қарастырылған жағдайда
 сипаттауыш санның рангі
сипаттауыш санның рангі
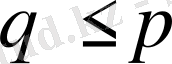 тең.
тең.
Енді
 сипаттауыш сан үшін ранг
сипаттауыш сан үшін ранг
 деп алайық.
деп алайық.
 ретті минорды
ретті минорды
 қатары бойынша жіктеп және оған
қатары бойынша жіктеп және оған
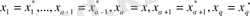 ,
,
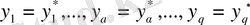
деп аламыз, мұнда
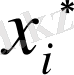 және
және
 кез-келген сан, бірақ мұндай
кез-келген сан, бірақ мұндай
 -ші минордың реті нөлге тепе-тең бола алмайды.
-ші минордың реті нөлге тепе-тең бола алмайды.
Сонда (2. 1. 6) формадағы минордың өрнегі
 болғандағы қосылғыш қосындыда жоғалып, яғни
болғандағы қосылғыш қосындыда жоғалып, яғни
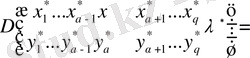
аламыз.
(2. 1. 6) біртекті интегралдық теңдеудің шешімінен
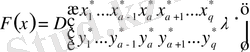
функциясын алуға болады, мұнда
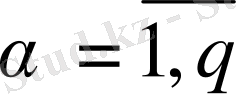 , яғни
, яғни
 әртүрлі шешімдері бар болады. Алынған шешімдерді
әртүрлі шешімдері бар болады. Алынған шешімдерді
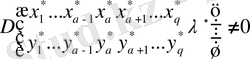 бөлейік және (2. 1. 6) теңдеу қаншалықты біртекті болса, онда функция
бөлейік және (2. 1. 6) теңдеу қаншалықты біртекті болса, онда функция
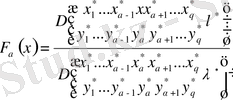 , (2. 1. 10)
, (2. 1. 10)
Мұнда
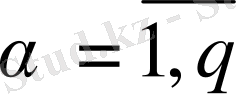 оның шешімдері болып табылады.
оның шешімдері болып табылады.
Анықтама
. (2. 1. 10) формуладығы
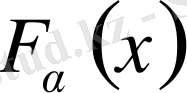 функциясын
функциясын
 сипаттауыш санның фундаментальды шешімдері деп атаймыз.
сипаттауыш санның фундаментальды шешімдері деп атаймыз.
(2. 1. 10) формуладан фундаментальды функцияның өте маңызды екі қасиеті шығады.
1)
 , 2)
, 2)

 (2. 1. 11)
(2. 1. 11)
демек бірінші жағдайда алымы бөліміне тең, ал екіншіде алымында екі бірдей қатар пайда болады [8] .
2. 2 СЫЗЫҚТЫҚ ТӘУЕЛСІЗДІК ЖӘНЕ ФУНДАМЕНТАЛЬДЫ
ФУНКЦИЯЛАР ЖҮЙЕСІНІҢ ШЕШІМДЕРІНІҢ ТОЛЫҚТЫҒЫ
Алдымен (2. 1. 10) фундаментальды функцияның сызықтық тәуелсіздігін, (2. 1. 11) формуланың қасиеттерін пайдаланып және кері жору әдістерімен дәлелдейік.
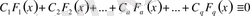
деп алсақ, мұнда
 барлықтары да нөлге тең емес. Сондықтан соңғы теңдікте тепе-теңдік орындалуы мүмкін, онда
барлықтары да нөлге тең емес. Сондықтан соңғы теңдікте тепе-теңдік орындалуы мүмкін, онда
 деп алсақ (2. 1. 11) формуладағы екінші қасиет негізінде
деп алсақ (2. 1. 11) формуладағы екінші қасиет негізінде
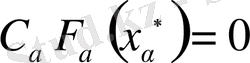 аламыз, бірінші қасиет салдарынан
аламыз, бірінші қасиет салдарынан
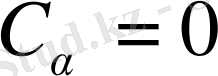 , бірақ
, бірақ
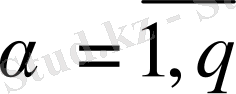 , яғни
, яғни
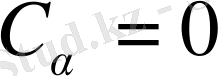 барлығы және бұдан сызықтық тәуелсіздік дәлелденді.
барлығы және бұдан сызықтық тәуелсіздік дәлелденді.
Енді шешімнің толықтығын дәлелдейік, яғни кез-келген
 сипаттауыш санға сәйкесті басқа да шешімдері сызықтық және біртекті фундаментальды функция арқылы өрнектелетіндігін көрсетейік [4] .
сипаттауыш санға сәйкесті басқа да шешімдері сызықтық және біртекті фундаментальды функция арқылы өрнектелетіндігін көрсетейік [4] .
(2. 1. 6) теңдеудің тағы да бір шешімін
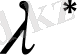 сипаттауыш санға сәйкесті
сипаттауыш санға сәйкесті
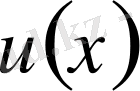 -функциясы деп алайық, сонда келесі тепе-теңдік орындалады
-функциясы деп алайық, сонда келесі тепе-теңдік орындалады
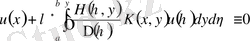 . (2. 2. 12)
. (2. 2. 12)
Әзірше анықталмаған бірақ үзіліссіз емес
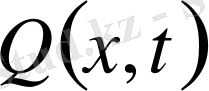 енгізейік және келесі тепе-теңдікті жазайық
енгізейік және келесі тепе-теңдікті жазайық
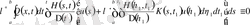 . (2. 2. 13)
. (2. 2. 13)
Содан соң (2. 2. 12) -дағы
 ді
ді
 ге,
ге,
 ті
ті
 ге алмастырып, (2. 2. 12) тепе-теңдіктен (2. 2. 13) тепе-теңдікті шегеріп және олардың қосындысын бір интегралға біріктіріп, екінші қосылғыштағы
ге алмастырып, (2. 2. 12) тепе-теңдіктен (2. 2. 13) тепе-теңдікті шегеріп және олардың қосындысын бір интегралға біріктіріп, екінші қосылғыштағы
 ті
ті
 ге,
ге,
 ны
ны
 ге ауыстырып,
ге ауыстырып,
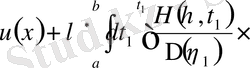
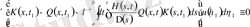 .
.
Тік жақшалы өрнектегі белгісіздерді
 арқылы белгілейміз:
арқылы белгілейміз:
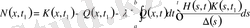 ,
,
сонда
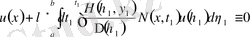 . (2. 2. 14)
. (2. 2. 14)
Бұдан әрі
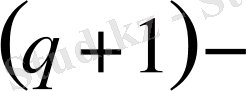 ші минорды
ші минорды
 бағаны бойынша оның құрамына кіретін анықтауыштарды (2. 1. 5) теңдеумен сәйкесті жіктелуін жазайық
бағаны бойынша оның құрамына кіретін анықтауыштарды (2. 1. 5) теңдеумен сәйкесті жіктелуін жазайық
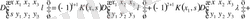
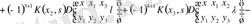
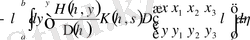 .
.
Алынған жіктеуді екіншіден бастап, барлық мүшелерін теріс таңбалы болатындай қатарды алмастырып, ал минорды
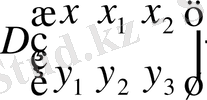 оған тең болатындай
оған тең болатындай
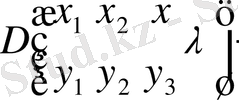 алмастырсақ, онда
алмастырсақ, онда
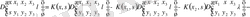
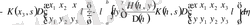 .
.
аламыз.
Аналогиялық түрде
 болғанда (2. 1. 5) жіктеудің жалпы түрін
болғанда (2. 1. 5) жіктеудің жалпы түрін
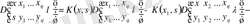

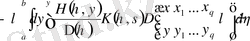 . (2. 2. 15)
. (2. 2. 15)
жазамыз.
(2. 2. 15) минорының жіктелуін
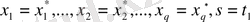 ,
,
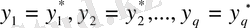 ,
,

деп аламыз.
 белгісі арқылы белгіленген санда минор
белгісі арқылы белгіленген санда минор
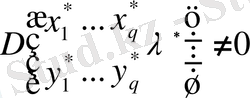
болатындай етіп таңдаймыз және оны (2. 2. 15) теңдігін белгілейміз:
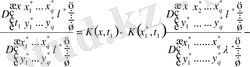
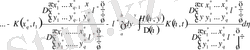 .
.
Соңғы теңдіктегі бөлшекті сол жақтан
 үшін алайық, ал қалған бөлшектің (2. 1. 10) формулаға сәйкесті
үшін алайық, ал қалған бөлшектің (2. 1. 10) формулаға сәйкесті
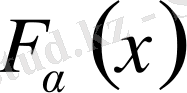 фундаментальды функциялары бар
фундаментальды функциялары бар
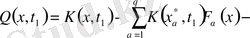
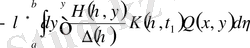 .
.
Соңғы теңдіктен
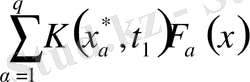 анықтап, біруақытта
анықтап, біруақытта
 ті
ті
 ға және
ға және
 ді
ді
 ке (2. 2. 14) тепе-теңдікке сәйкесті белгілеулермен ауыстырамыз
ке (2. 2. 14) тепе-теңдікке сәйкесті белгілеулермен ауыстырамыз
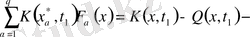
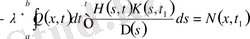 .
.
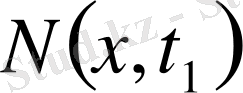 үшін алынған өрнекті (2. 2. 14) тепе-теңдігіне қоямыз:
үшін алынған өрнекті (2. 2. 14) тепе-теңдігіне қоямыз:
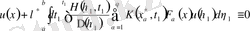
немесе
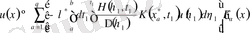 .
.
Тік жақшалы соңғы тепе-теңдіктен интегралды есептеуден соң тұрақты сандарды аламыз, оларды
 арқылы белгілесек, сонда
арқылы белгілесек, сонда
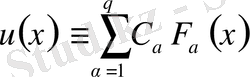 ,
,
яғни (2. 1. 6) теңдеудің кез-келген шешімі біртекті фундаментальды функция арқылы және сызықтық түрде өрнектеледі, шындығында алынған фундаментальды функциялар жүйесі толық болады [8] .
Енді Фредгольм теоремасының екінші аналогын тұжырымдайық.
Егерде

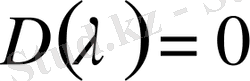 теңдеуінің түбірі болса, рангі
теңдеуінің түбірі болса, рангі
 тең, онда (2. 1. 6) біртекті шешілетін интегралдық теңдеудің
тең, онда (2. 1. 6) біртекті шешілетін интегралдық теңдеудің
 сызықтық тәуелсіз шешімдері бар, бұл
сызықтық тәуелсіз шешімдері бар, бұл
 мәніне сәйкесті және (2. 1. 10) формуламен анықталады, ал бұл теңдеудің кез-келген шешімі олар арқылы сызықтық және біртекті болып өрнектеледі.
мәніне сәйкесті және (2. 1. 10) формуламен анықталады, ал бұл теңдеудің кез-келген шешімі олар арқылы сызықтық және біртекті болып өрнектеледі.
Мысал 4 . Теңдеудің жалпы шешімін
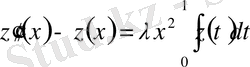
және шешілетін теңдеудің фундаментальды функция жүйесін тап.
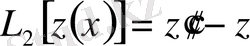 ,
,
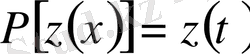 ,
,
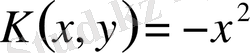
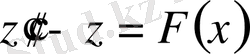 ,
,
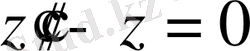 ,
,
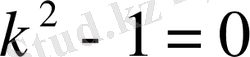 ,
,
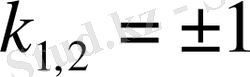 ,
,
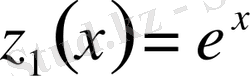 ,
,
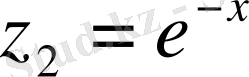 ,
,
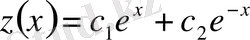 .
.
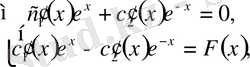
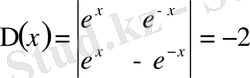 ,
,
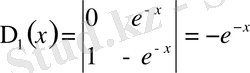 ,
,
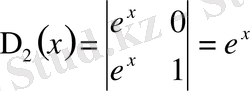 ,
,
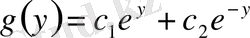 ,
,
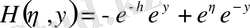 ,
,
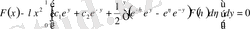 .
.
(1. 2. 29) және (2. 1. 2) қатарлар коэффициенттері
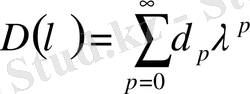 ,
,
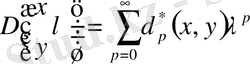
(1. 2. 33) және (1. 2. 34) формулалар бойынша табамыз
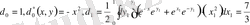 ,
,
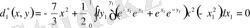 ,
,
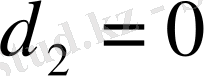 ,
,
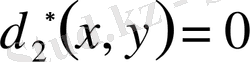 және тағы басқа.
және тағы басқа.
Сондықтан,
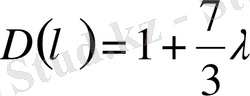 ,
,
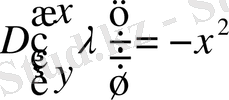 ,
,
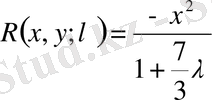 (1. 1. 20) және (1. 1. 9) формула бойынша анықтаймыз
(1. 1. 20) және (1. 1. 9) формула бойынша анықтаймыз
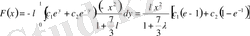 ,
,

 .
.
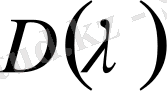 нөлге теңестіре отырып
нөлге теңестіре отырып
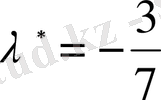 ,
,
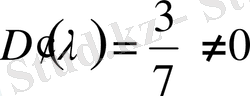 сипаттауыш мәндерін табамыз, сондықтан сипаттауыш санның рангы
сипаттауыш мәндерін табамыз, сондықтан сипаттауыш санның рангы
 және
және
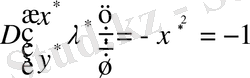 ,
,
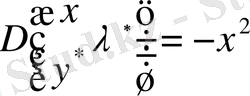 ,
,
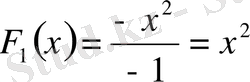 , яғни шешілетін теңдеудің фундаментальды функциясының жүйесі
, яғни шешілетін теңдеудің фундаментальды функциясының жүйесі
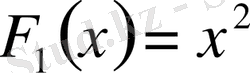 және
және
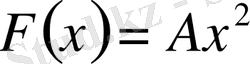
функцияларының бірінен тұрады.
Бастапқы есепті бастапқы шарттармен (1. 1. 1) интегралдық дифференциалдық теңдеу үшін қарастырамыз
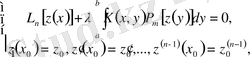 (1. 1. 1)
(1. 1. 1)
мұнда
 ,
,
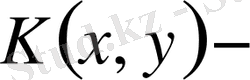 өзгешеленген ядро.
өзгешеленген ядро.
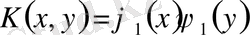 болсын, сонда (1. 1. 10) шешілетін теңдеу
болсын, сонда (1. 1. 10) шешілетін теңдеу
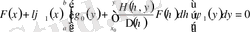
немесе
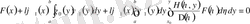
жазылады, мұнда
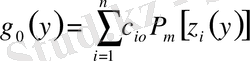 ,
,
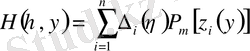 .
.
Бұдан әрі біртекті интегралдық теңдеуге сәйкесті
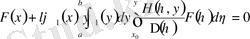 ,
,
қарастырамыз, егерде
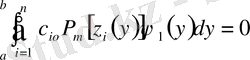 деп алсақ.
деп алсақ.
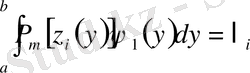 интегралын есептеуден соң
интегралын есептеуден соң
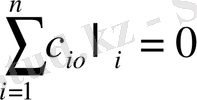 , яғни
, яғни
 тұрақтыларын біртекті теңдеулердің сызықтық тәуелсіздік жағдайларында аламыз және
тұрақтыларын біртекті теңдеулердің сызықтық тәуелсіздік жағдайларында аламыз және
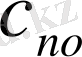 арқылы қалғандарын өрнектеуге болады:
арқылы қалғандарын өрнектеуге болады:
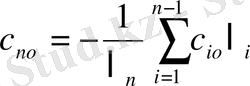 .
.
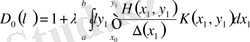
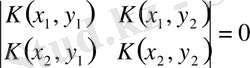 ,
,
демек
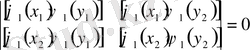 .
.
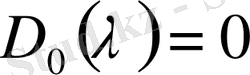 теңестіріп рангі
теңестіріп рангі
 тең болатын
тең болатын
 сипаттауыш санын табамыз және
сипаттауыш санын табамыз және
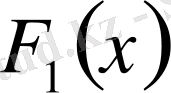 бір фундаментальды функциясын табамыз. Біртекті теңдеудің жалпы шешімі
бір фундаментальды функциясын табамыз. Біртекті теңдеудің жалпы шешімі
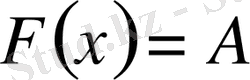
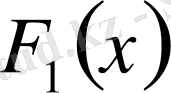 , мұнда
, мұнда
 - кез-келген тұрақты.
- кез-келген тұрақты.
(1. 1. 1) біртекті теңдеудің жалпы шешімін
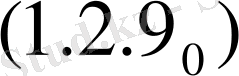 формула бойынша табамыз
формула бойынша табамыз
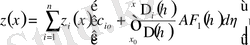 ,
,
мұнда
 тұрақтылардың бірі қалғандары арқылы табылады, сонымен бастапқы есепті шешу барысында қарама қайшылық туындаған жоқ,
тұрақтылардың бірі қалғандары арқылы табылады, сонымен бастапқы есепті шешу барысында қарама қайшылық туындаған жоқ,
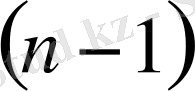 шартын жеткілікті түрде беруде
шартын жеткілікті түрде беруде
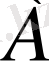 тұрақтысы анықталмаған болып қалады, яғни Коши есебінің шешімінің жалғыздығын бұзады [5] .
тұрақтысы анықталмаған болып қалады, яғни Коши есебінің шешімінің жалғыздығын бұзады [5] .
Мысал 5. Коши есебінің арнайы шешімін табу.
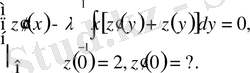
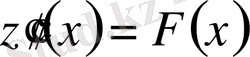 ,
,
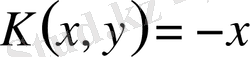 ,
,
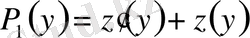 .
.
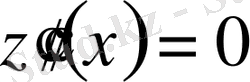 ,
,
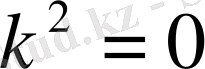 ,
,
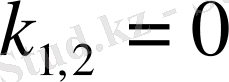 ,
,
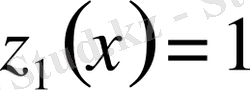 ,
,
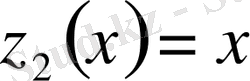 ,
,
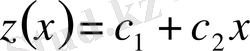 .
.
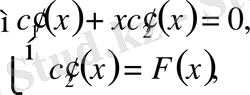
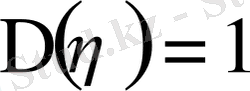 ,
,
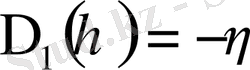 ,
,
 ,
,
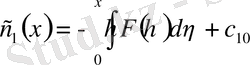 ,
,
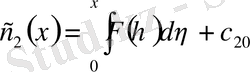 .
.
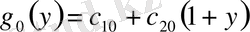 ,
,
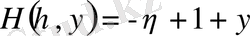 ,
,
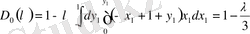 .
.
 сипаттауыш сан және (1. 1. 10) теңдеу
сипаттауыш сан және (1. 1. 10) теңдеу
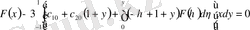
жазылады.
Біртектілік шарттан
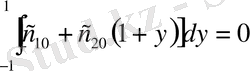 жазып,
жазып,
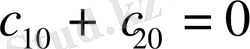 немесе
немесе
 табамыз. Біртекті теңдеу
табамыз. Біртекті теңдеу
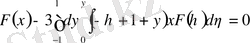
болады.
Бұдан
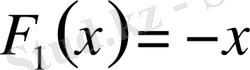 және біртекті теңдеудің жалпы шешімі
және біртекті теңдеудің жалпы шешімі
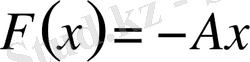 түрінде жазылады. Бұдан әрі алдымен
түрінде жазылады. Бұдан әрі алдымен
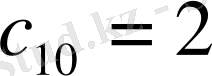 және
және
 анықтай отырып, мамандандырылған шешімді табуға болады
анықтай отырып, мамандандырылған шешімді табуға болады
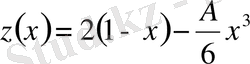 .
.
3 ФРЕДГОЛЬМ ТЕОРИЯСЫНЫҢ ҮШІНШІ АНАЛОГЫ
3. 1 ЕКІ ШЕШІЛЕТІН ИНТЕГРАЛДЫҚ ТЕҢДЕУЛЕРДІҢ
ШЕШІМДЕРІ АРАСЫНДАҒЫ БАЙЛАНЫС
Алдында біз (1. 1. 1) интегралдық диффенренциалдық теңдеулердің екі шешілетін интегралдық теңдеулердің (1. 1. 10) және
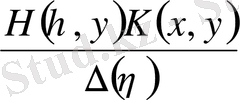 ядролы және (1. 2. 22) Фредгольм теңдеуін
ядролы және (1. 2. 22) Фредгольм теңдеуін
 ядросымен алғанбыз. Олар арқылы байланыс құрайық. Фредгольм теоремасына [6] сәйкесті (1. 2. 22) теңдеудің бірінші және жоғарғы ретті детерминантты қатарларын
ядросымен алғанбыз. Олар арқылы байланыс құрайық. Фредгольм теоремасына [6] сәйкесті (1. 2. 22) теңдеудің бірінші және жоғарғы ретті детерминантты қатарларын
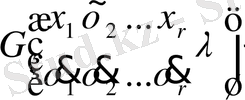 :
:
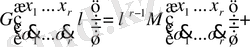
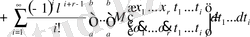 . (3. 1. 1)
. (3. 1. 1)
(1. 2. 22) теңдеудегі
 ядросының белгілеуімен сәйкесті детерминанттар өрнегін жазайық
ядросының белгілеуімен сәйкесті детерминанттар өрнегін жазайық
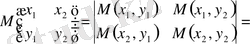
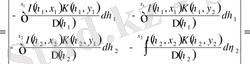
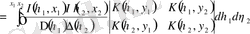 , (3. 1. 2)
, (3. 1. 2)
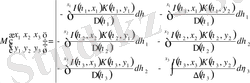
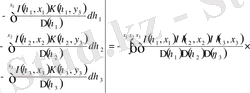
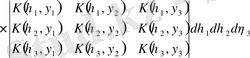 , (3. 1. 3)
, (3. 1. 3)
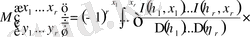
 , (3. 1. 4)
, (3. 1. 4)
(3. 1. 1) формуласын
 үшін қолдана отырып бірінші ретті Фредгольмнің детерминантты қатарының түрлендірулерінен бастайық:
үшін қолдана отырып бірінші ретті Фредгольмнің детерминантты қатарының түрлендірулерінен бастайық:
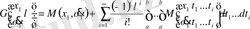 (3. 1. 5)
(3. 1. 5)
(3. 1. 4) өрнекті (3. 1. 5) қоямыз:
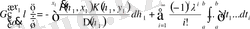 .
.
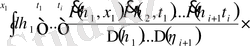
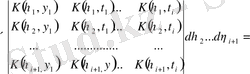
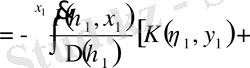
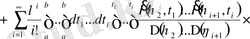
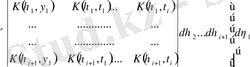 .
.
Тік жақшадан
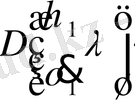 (1. 2. 28) формуласына сәйкесті алуды байқау киын емес, сонда
(1. 2. 28) формуласына сәйкесті алуды байқау киын емес, сонда
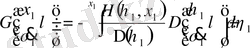 . (3. 1. 6)
. (3. 1. 6)
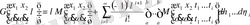
үшін аналогиялық есептеу жасаймыз, Фредгольмнің екінші шекті қатарының детерминантын табамыз
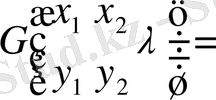
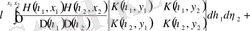
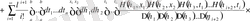

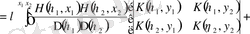
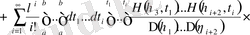
 ,
,
(2. 1. 1) өрнегіне сәйкесті квадратты жақшадағы оның мәнімен
 алмастырып
алмастырып
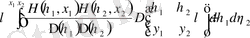 . (3. 1. 7)
. (3. 1. 7)
аламыз.
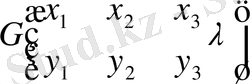
үшін аналогиялық түрде қатынасты алуға болады
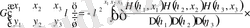
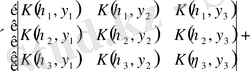
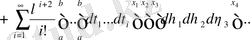
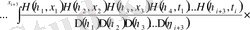

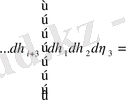
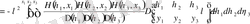 , (3. 1. 8)
, (3. 1. 8)
және индукция бойынша
 ші ретті детерминантты қатар үшін қатынасты жазамыз
ші ретті детерминантты қатар үшін қатынасты жазамыз
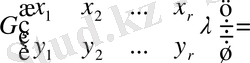
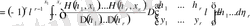 ,
,
 (3. 1. 9)
(3. 1. 9)
Бұрынырақ алынған (1. 1. 10) және (1. 2. 22) екі шешілетін интегралдық теңдеулердің шешімдері арасындағы байланысты құру үшін алдымен (1. 1. 1) интегралдық дифференциалдық теңдеу үшін мына теңдеулерді жазамыз
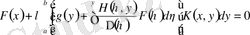
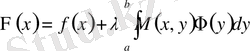 ,
,
мұнда
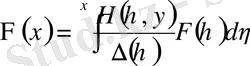 ,
,
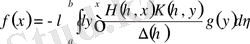 ,
,
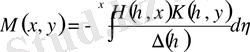 .
.
(1. 1. 10) теңдеудегі
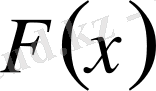 шешімі табылса, онда (1. 2. 25) теңдеудегі белгілеулерді қолдана отырып оның шешімдерін табамыз. Ал керісінше, егерде (1. 2. 25) теңдеудегі
шешімі табылса, онда (1. 2. 25) теңдеудегі белгілеулерді қолдана отырып оның шешімдерін табамыз. Ал керісінше, егерде (1. 2. 25) теңдеудегі
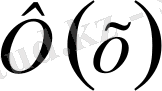 шешімі белгілі болса, онда (1. 2. 21) теңдеуді ескеріп және оны (1. 1. 10) теңдеуге қойып,
шешімі белгілі болса, онда (1. 2. 21) теңдеуді ескеріп және оны (1. 1. 10) теңдеуге қойып,
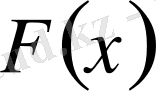 шешімін табамыз
шешімін табамыз
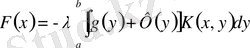 . (3. 1. 10)
. (3. 1. 10)
Егерде
 сипаттауыш сан болмаса, онда (1. 1. 10) теңдеудің шешімі (1. 2. 25) теңдеу түрінде жазылады
сипаттауыш сан болмаса, онда (1. 1. 10) теңдеудің шешімі (1. 2. 25) теңдеу түрінде жазылады
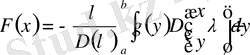 .
.
Егерде енді (1. 2. 25) -ні (1. 2. 21) формуладағы
 үшін қойсақ, онда (1. 2. 22) теңдеудің шешімін аламыз
үшін қойсақ, онда (1. 2. 22) теңдеудің шешімін аламыз
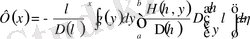 , (3. 1. 11)
, (3. 1. 11)
бірақ бұл (1. 2. 22) теңдеудің шешімін Фредгольмнің тікелей формуласы бойынша алуға болады
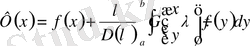 . (3. 1. 12)
. (3. 1. 12)
Енді (3. 1. 12) (3. 1. 10) қоямыз
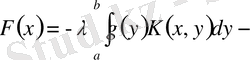
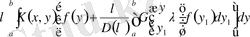
және (3. 1. 6) формула бойынша
 детерминантын
детерминантын
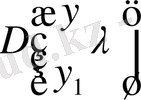 ауыстырып бұрынырақ белгілі болған
ауыстырып бұрынырақ белгілі болған
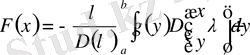
келеміз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz