Тригонометриялық функциялар

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 55 бет
Таңдаулыға:

КІРІСПЕ

Тарих пәніне үңіліп, оған назар аударған кез келген индивид мынадай логикалық көсе-көлденең сұрақтарға тап болуы ғажап емес. Жалпы Адам ата жаралғанна бергі оның біздерге келіп жеткен тарихи мәліметтері? Оны көптеген философтар, зерттеушілер, антропологтар, генетиктер, теологтар зерттеген, зерттеп те жатыр. Яғни, олай болса, тарих пәнінің өзі де осы айтылып өткен ғылым салаларының тармақтарына жүгінетіні даусыз. Ақиқат пен таным теориясының анықтамалары бойынша:

(Зерттеліп отырған, объекті жөніндегі толық емес білімді салыстырмалы ақиқат, ал толық және дәл білімді абсолюттік ақиқат деп атайды. Салыстырмалы ақиқат пен абсолюттік ақиқат әлеуметтік, тарихи процесс ретіндегі объективтік ақиқаттың көрініс сәттері. Объективтік ақиқат салыстырмалы - абсолюттік формада ғана өмір сүреді) . Тарих баспалдағы Жер планетасының пайда болуынан туындайды, сондай-ақ алғашқы бір клеткалы, сонан соңғы жерде биологиялық даму кезеңдеріне байланысты материалистік көзқараста маймылдан адамға ауысу сатысымен шенеледі. Ал дін этаптарына тоқталсақ, табиғат, барлық планеталар жер панетасындағы барлық тіршілік элементтері. Алла-тағаланың, құдіреті күшті бір құдайдың жаратқанын ескереміз.

Сонда тарих деген пәнді зерттеуге оның жалғыз өзінің қауқары жетпейтінін көруге болады, (географиялық орта, территориялық, этникалық шекаралар, дін, шаруашылық-экономикалық, саяси-әлеуметтік) факторлардың жемісі деп көруге болады. Қазақ халқының белгілі бір этаптағы арғы-бергі тарихына тоқталсақ, бір қарағанда жариялауға ауыр соғады. Ғұндар, Сақтар, Үйсіндер (б. д. д. ІІІ ғ. -б. д. ІІІ ғ. ), Оғыздар мен Қидандар (8-9 ғ. ғ. ), Моңғолдар (12-14 ғ. ғ. ), тіпті кейінгі Жоңғарлардан (17-18 ғ. ғ. ) әскери стратегия мен тактика талабынан тарих зерттеушілері уағыздайды. Ғалымдар мен зерттеушілер географиялық детерменизмнен, яғни, қоғам мен өркениет тағдырына жер жағдайы, климат, тағы сол сияқты, бір сөзбен айтқанда табиғи ортаның әсерін бағалаудан қаша отырып, керісінше географиялық нигилизмге (Л. Н. Гумилев), жеткізгенде табиғи ортаның маңызын мүлдем есепке алмауға ұрынғандығын байқамай да қалатыны бар. Бұл бойынша Қазақстан территориясы физикалық-географиялық сипаттамасы жағынан негізгі үш бөліктен тұрады. (В. М. Чупахин Физическая география Казахстана. А-Ата -1968. стр11-12) Батыс, Солтүстік Батыс Қазақстан - шөлейтті, ойпат далалы; Солтүстік және Орталық Қазақстан - далалық, шүйгін жайылымды, таулы; Оңтүстік, Оңтүстік Шығыс Қазақстан өзенді-көлді, жайылымды, таулы. Осындай этнотерритриялық дәріптеулер, тарих пәнін математикалық аспектілер бойынша нақтыландырруға көмек көрсетеді. Негізгі қарастырылып отырған тақырыпты жоғарыда айтылып өтілген көзқарастармен және де математикалық мектеп программасынан аспайтын заңдылықтармен дәлелдеп сынға алуға тырысайық. Тарихи деректерді зерттеп жарыққа осы тақырыпты (Қазақ әдебиеті, 16 қазан 1992 жыл) Қарағандды мемлекеттік университетінің оқытушысы, профессор Талғат Әбдіразақов шығарған. Ал, бұл мақаладағы жарияланатын жұмыстың негізгі сипаттамасы, Талғат Әбдіразақовтың мақаласына (математикалық, логикалық, информатикалық) тұрғыда мектеп қабырғасында математика тарих пән аралық байланысының бір бөлігін насихаттау. Негізгі бөлімнің маңызы, мынандай сұрақтың айналасындағы зерттеулерден тұрады: Қазақтар мен Жоңғарлар арасындағы ұзаққа созылған жаугершіліктің төркіні неде? 150 млн. Жыл бұрын Қазақстан территориясының орнында Тэтип мұхиты болғанның әсерінен де көп нәрсе туындайды.

1 МЕКТЕП КУРСЫНДА ТРИГОНОМЕТРИАЛЫҚ ФУНКЦИЯЛАРДЫ ҮЙРEНУДІҢ ЖАЛПЫ МӘСЕЛЕЛЕРІ

1. 1 ТРИГОНОМЕТРИАЛЫҚ ФУНКЦИЯ ТУРАЛЫ ҚЫСҚАША ТАРИХИМАҒЛҮМАТТАР

Көне заманда тригонометрия астрономияның, жер өлшеуінің, суда жүзу және құрылыс жұмыстарының сұраныстарына байланысты пайда болды. Қандайда бір элементтер арқылы есептеу әдістерін ойлап табуға алып келеді.

Мысалы, олардың көмегімен қол жетпейтін заттарга дейінгі қашықтықты анықтау және географиялық карталарды құрастыруға арналған жергілікті жердің геодезиалық көшірмесін жасау жұмыстары бір қатар оңайлатылды.

Тригонометриалық танымдардың негізі ежелгі заманда пайда болды. Бастапқы кезде тригонометрия астрономиямен тығыз байланыста дамыды, оның көмекші тарауы болды.

«Тригонометрия» атауының өзі грек сөзінен аударғанда «үшбұрыштарды өлшеу» деген ұғымды білдіреді.

Ежелгі грек ғалымы, белгілі астроном Птолемей ( ІІғ. ) «Алмагест» атты еңбегінде жазғандай, «хорда тригонометриясын» ойлап тапты. Птолемей жарты және екі еселенген бұрыштың, екі бұрыштың қосындысы мен айырымының қазіргі кездегі формулаларына мәндес болатын шеңбердің sdsdsd хордалары арасындағы (ол кезде математикалық белгілеулер қолданылмағандықтан, есептерді шығару жолы сөзбен жазылған) келесі қатынастарды шығарды:

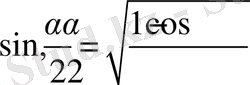
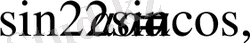
яғни таза геометриялық сипатта болады және негізінен хордаларды есептеуді» кұрады. Уақыт озуымен оған біртіндеп кейбір аналитикалық моменттер ене бастады. [1-7]

Хордаларды синустармен ауыстырып, тригонометрияның әрі қарай дамуына Үндістандық ғалымдар үлкен үлес қосты. Бұл жаңа енгізу VIII ғасырда тригонометрияны бірте-бірте астрономия тарауынан бөліп алып, жеке ғылымға айналдырды. Олараб тіліндегі жақын және алыс Батыс мемілекеттерінің математикасына ауысты. Синустан басқа тригонометриялық функциялар да енгізілді және олар үшін де кестелер күрылды.

Тригонометрияны өзіндік ғылыми пэн ретінде қалыптастыруда ІХ-ХІІІ ғасырлардағы Орта азиялық ғалымдардың еңбектері орасан зор. Орта азиялық математиканың дамуы астрономия, география, геодезия үсынған есептеу тапсырмаларын шешу қажеттілігімен тығыз байланысты болады. Сондықтан тригонометрия өзіндік зерттеу эдістері бар жеке ғылым, оның мақсаты қарапайым геометриалық фигуралардың элементтерін, жазық және сфералық үшбұрыштарды есептеу тэсілдерін табу болды. Тригонометриялық функциялар туралы ілім геометрия негізінде жасалды. Геометриялық тәсілдермен орындалған тригонометриялық функциялар арасындагы алгебралық қатыстар осы функцияларды зерттеуге, алгебралық тәсілдерді қолдануға, түрлендірулер жүргізуге, геометриялық фигуралардың элементтердің арасында әртүрлі қатынастарды қорытуга мүмкіндік берді. Осылайша геометрияға негізделген және алгебралық әдістерді кең қолданатын тригонометрияға ерекше сипаттамг берілді.

Тригонометрия туралы жалпы ұғымдар, тригонометриялық функциялардын белгілеулері және анықтамалары ұзақ тарихи даму процесінде қалыптасты. Негізгі тригонометриялық ұғымдарды енгізу кезінде тригонометриялық дөңгелектің радиусын 1 -ге тең деп алу оңай тәрізді, бірақ бұл қарапайым идея Х-ХІ гасырларда ғана игерілді. Егер біз тікбұрышты үшбұрыштағы α бұрышының синусы қарсы жатқан ВС катетінің ОС гипотенузасына қатынасы деп түсінсек, онда орта ғасырда «синус» терминін ВС синус сызығының өзі деп белгіледі. Тура осылай косинусты да, ОВ косинусының сызығы деп және баска да тригонометриалық функцияларды осылай түсінген.

Ғылымның әрі қарай дамуы тригонометриялық функциялардың периоттык процестерді игеру кезінде физикада, техникада маңызды мэні бар екенін көрсетті. Ж. Фурье қандайда бір периодтық қозғалысты кез келген дәлдікпен қарапайым синусоидалық тербелістің қосындысы түрінде беруге болатынын дәлелдеді. Сондықтан тригонометрияның мазмұны кеңейді, өйткені ондағы сая аргументіне қатысты тригонометриялық функцияларды зерттеу өзіндік мәнге ие болды.

1. 2 МЕКТЕП КУРСЫНДА -ЛАРДЫ ҮЙРЕНУДІҢ ЖАЛПЫ МӘСЕЛЕЛЕРІ

Кіріспеде алгебра және анализ бастамаларының мектеп курсында тригонометриялық функцияларды оқытудың қажеттілігі туралы айтылды. Бұл қажеттілікке не себепші?

Сонымен, тригонометриялық функцияларын оқытудың негізгі мақсаттары:

1) оқушыларды функциялардың жаңа түрілерімен таныстыру;

2) есептеу практикасының дағдыларын дамыту (функциялармен жүмыс көбінесе көп есептеулерді талап етеді) ;

3) функцияның барлық негізгі қасиеттерін көрнекі иллюстрациялау (эсіресе периодтығын) ;

4) практикамен байланыстарды тагайындау (маятник тербелісін, электр тогын, жарықтың толқындық теориясын оқыту тригонометриялық функцияларсыз мүмкін емес) ;

5) логикалық пікірлеуді дамыту (формулалардың көптігі зерттеу сипатындагы алгебралық сипатта болмайтын түрлендірулер қажеттілігін туғызды) ;

Тригонометриялық функцияларды үйренуде келесі басқыштарды атап көрсетуге болады.

Геометриядагы бүрыштық аргументті тригонометриялық функциялармен алгашқы танысады. Аргумент мэні (0°, 90°) аралыгында қарастырылады. Бұл бүрышқа оқушылар, оның градустық шамасына байланысты, кестелік мәндермен, негізгі тригонометриялық тепе-теңдікпен және кейбір келтіру формулаларымен танысады.
(0°, 180°) бүрыштары үшін синус, косинус, тангенс жәнекотангенс үгымдарын жалпылау. Бұл басқышта тригонометриялық функцияларының және жазықтықтагы нүкте координаттары өзара байланыста қарастырылады, синустар және косинустар теоремалары дэлелденеді, үшбүрыштарды тригонометриялык қатынастар арқылы шешу мәселесі қарастырылады.

III. Сандық аргументтік тригонометриялық функциялар үғымын енгізу.

Тригонометриялық функцияларды анықтаудың бірнеше тәсілі бар екендігін ескереміз. Оларды екі топқа бөлуге болады: аналитикалық және геометриялык.

Аналитикалық тэсілге $y = \ \sin x$ функцияны $f"\ (x) = \ - c*\ f(x) $

дифференциалдық теңдеудің шешімі ретінде немесе

$\sin{x = x - x^{3}}/3! + x^{2}/5!. . \$ дәрежелік қатардың қосындысы ретінде анықталады. Геометриялық тэсілдерге тригонометриялық функцияларды проекциялаг және радиус-вектордың координаттар негізінде анықталғандарды, бүрышты үшбүрыштың қабырғаларының қатынасы арқылы анықтауды және сандык шеңбер көмегінде анықталады. Мектеп курсында басымдылық қарапайым жәве көрнекілігі себепті геометриялық тәсілдерге беріледі.

Мектеп курсында тригонометриялық функцияларды үйрену кейбір ерекшеліктерге ие болатынын ескереміз. [8-15]

Біріншіден, тригонометриялық функцияларды үйренуге дейін, у = f(х) түріндегі функция қарастырылады, ал Бұл оқушылар үшін біршама міндетке сай емес болады. Бүдан басқа, алдын барлық функциялар формулалармен берілетін, онда айқын түрде функция мэнін алу үшін аргумент мәндері үстінде оқушылар кестелік түрде берілген функцияларға кездеседі.

Сонымен, тригонометриялық функцияларды оқытуда оқушылар функция үғымыныц мән-мағынасын дүрыс түсіне бастайды. Олар, кез келген обьектілер жиындарыныц арасындағы байланыс, егер әртүрлі табиғатқа ие болса да, (тек аргументтің әрбір мэніне функцияның бір ғана мэні сәйкес келетін болса) функция болатынын түсіне бастайды.

1. 3 ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАР

Алгебра және анализ бастамалары курсында «тригонометриялық функциялар» тақырыбын оқыту әдістемесі

Мектепте тригонометриялық функцияларды оқытуда екі негізгі басқышты атап өтуге болады.

Геометрия курсында (8-9сынып) бұрыштық аргументтің тригонометриялық функциялармен алғашқы танысу.

Алгебра және анализ бастамалары курсында (9-10 сынып) тригонометриялық функциялар туралы білімдерді кеңейту және жүйелеу.

Бірінші басқышта оқытылатын байланыстар функциялар екендігі дәлелденбейді және анықталмайды. Бүрыштың өзгеруінде синус және косинустың өзгеруінің қасиеттері негізінде дэлелденеді.

Бұл үғымдар геометрия курсы үшін жеткілікті түрде абстракті, сондықтан жақсы меңгерілмейді және 90-градустан жоғары аргументке өту үлкен қиыншылықтар тудырады. Себебі, біз тригонометриялық функцияларды тікбүрышты үшбүрыштың қабырғаларының қатынасы арқылы анықтадық, ал тікбүрышты үшбүрышта 90- нан үлкен градустық өлшемдегі бүрыштың болмайтындығы белгілі. Осы факті түсіндіру үшін осы басқышта шеңберді қарастыруға тура келеді жәнеБұл алгебра және анализ бастамалры курсында сан аргументті тригонометриялық функциялар шеңбер көмегінде енгізу үшін өзіне тэн жүмыс болып табылады.

Екінші басқышта бүрыштық аргументтен сандыққа өту жүргізіледі. Курстың басынан кез келген шамадағы бүрыштық тригонометриялық функцияларын қарастыруымыз керек. Демек, оқушыларды алдын ала бұрыштан -∞ тен +∞ -ге дейін өзгере алатын шама екендігімен таныстыру керек. Геометрия курсында бұндай ұғым жоқ болатын, сондықтан бұны екінші басқышта толықтыру қажет. Сонымен сандық шеңберді енгізу қажеттілігі туындайды және екінші басқышта өткізген мақсатқа сай.

Сандық шеңбердің моделін үйрену үшін пропедевтикалық жұмыстар сипатында берілген радиустағы шеңбердің ширек жарты және үштен бір ұзындықтағы доғасын табуға арналған геометриялық есепті қарастырған жөн. Алынған нэтижелерді жалпылап, оқушыларды алдындағы жүмыстар үшін кез келген радиуыстағы емес, бірлік радиуыстағы шеңберді таңдаған тиімді екендігіне әкелу қажет.

Сандық шеңбермен жүмыс процесінде оқушыларда келесі біліктіліктер қалыптасқан болуы керек;

Сандық шеңберде п санының үлестерінде өрнектелген және п санының үлестерінде өрнектелмеген, берілген сандарға сәйкес келетін нүктелерді табу;

Сандық шеңбердің доғасы үшін аналитикалық жазуларды құрастыру;

Бір мезгілде екі координат жүйесінде жұмыс істеу - қисық сызықты және тік бүрыштыны табу;

Декарттық және бір координат жүйесінен екіншісіне өтуді орындауды;

Сандық шеңберде нүктелердің координаттарын табуды және сандык шеңберде берілген координаттары бойынша нүктелерді табуды.

Бұл үшін келесі типтегі тапсырмаларды қарастырған мақсатқа сай:

Сандық шеңберде π/2, 9 π, 26 π/3, 5 π/4, 7 π/6, . . . нүктелерді тап
Сандық шеңберде 1, 2, -7, 4, 5, -31, . . . нүктелерді тап
21π/4, -37π/6, 10, -95 нүктелері қай ширектерге тиісті екендігін анықта

4) келесі теңсіздіктерді қанағаттандыратын t нүктелерін сандық шеңберде белгілеңіз.

a) π/6+2kπ≤t≤2π/3+2kπ; k∈Z

b) -π/3+2kπ≤t≤3π/4+2kπ; k∈Z

5) π/4, -З π/2, 23 π/6, -13 π/3, . . . сандарына сәйкес келетін нүктелердің декарттық координаттарын анықта

6) (1/2; √3/2) (-√2/2; / √2/2), (√3/2; -1/2), (-1; 0), . . . координаттар нүктелері сәйкес келетін оң және бүрыштарды сандарды тап.

7) Сандық шеңберде ординаталары √3/2, 1/2, - √2/2, 0 -ге тең болатын, ал абциссалары теріс болатын күктелерді тап және олар қай сандарға сәйкес екендігін жаз.

8) Сандық шеңберде √2/2 ординаттар нүктелерін тап және олар қай сандарға сәйкес келетінін жаз.

Сандық шеңбермен жүмыс істеу процесінде келесі моменттерге назар аудару керек.

Мүғалімнің қолында минимум екі сандық шеңбері бар макет болуы қажет. Олардың бірінде 0, π/6, π/4, π/6, π/2, 2π/3 нүктелері көрсетілген және есептеу оң бағытта жүргізілген болуы, ал екіншісінде, теріс бағытта және

0, -π/6, -π/4, -π/6, -π/2, -2π/3 нүктелері көрсетілген болуы керек, және де екінші макет оқушылардан « Егер нүкте оң бағытта емес, теріс бағытта қозғалатын болса, онда не болады?» деген сүраққа жауап беретін немесе жауап беруге әрекеттенетін болғаннан соң ілген жөн болады.

Бұл мотивациялық есеп сандық шеңбермен сандық түзу арасындағы байланысты жүргізуге мүмкіндік береді. Сандық түзуде тек оң мәндері емес, сондай-ақ теріс мәндері де, және де соншалықты үлкендерінде қоюға болады. Сандық шеңберді де осылай етуге болады, бірақ түзуде нүктелер арасындағы сәйкестік өзара бір мәнді, ал шеңберде әрбір нүктенің шексіз көп аттары болатынын, олар бір-бірінен 2πк -ға бүнда к е 2, айырмашылығы болатын фактін ескеру керек.

Бұл басты ерекшелікті оқушылар айқын түсінуі және сезінуі керек. Бұл үшін сандық шеңберді дөңгелекпен, ал сандық түзуді бойында нүктелер белгіленген шексіз үзын жіппен салыстыруы мүмкін.

Жіпті дөңгелекке орап, алдын-ала нөлдік нүктелерді сәйкестендіріп бірлік радиуыстағы сандық шеңбердің ұзындығы дэл 2π -ді қүрайтындығын 2п -мен өзгешеленетін нүктелер дөңгелекте бір орынға түсетіндігін байқауға болады. Шеңберде нүктелермен сандар арасындағы сәйкестіктің бірмәнді еместігімен байланысты проблема келесі түрдегі мәселені шешуде келіп

шығады: «Сандық шеңберде √3/2 -ден үлкен ординаталы нүктелерді табыңыз және олар қай сандарға сәйкес екендігін жазыңыз ».

Доғаны сипаттайтын бүндай теңсіздіктерді бастапқы басқышта екі қадамда қүрастырылу үсынылады. Бірінші қадамда, аналитикалық жазудың «ядросы» деп аталатын π/3<t<2π/3 -ті қүрастыру және тек екінші қадамда жалпы жазу π/3+2кπ<t<2π/3+2кπ -ны қүрастыру керек (мүндағы к∈Z) . Көптеген жағдайларда бүны шынында ешқандай кедергісіз орындауға болады, бірақ теңдеулердің немесе теңсіздіктердің шешімін анықтауда немесе функцияға белгілі бір шектеулерді қойғанда, к параметрі барлық а-ларды қабылдамауында, мысалы, тек оң немесе тек жүп мәндерді қалай болады?

+2πк жазуға бейімделген оқушылар к параметрі қандай мәндерді қабылдауын ойланбастан осындай жағдайда +2πк деп жазады, ал Бұл олардың шешімдерін автомат түрде қате деуге алып келеді.

Ал Бұл мысалы, 4πк, мүнда к ∈Z және 2πк, мүнда к е 2Z сәйкес деген фактіні түсінбеуіне алып келеді. Бұл өз кезегінде, периоды 4π -ға тең функцияларды қарастырғанда қиыншылықтарға алып келуі мүмкін.

Ал «Тригонометриялық функциялар» тақырыбын үйренуде бүндай функцияларға аз уақыт бөлінбейді.

Сонымен, ең кішкене деталдарға дейін, сандық шеңберді үйренуде ешқандай деталдарды назардан тыс қалдыруға болмайды, Бұл тригонометриялық функцияларды үйренуде білімдегі үлкен кемшіліктердің болуына себеп болуы мүмкін.

Тригонометриялық функцияларды сандық шеңбер көмегінде анықтау оқушылар санасында жақсы қабылданбайтындығын бір ғана қарапайым себеппен болатындығын естен шығармауы керек:бірінші басқышта анықтама геометриялық трактовкада (түсіндірмеде) берілген болатын тікбүрышты үшбүрыштың қабырғалар арасындағы қатынас ретінде.

Психологшдан белгілі: «Егер қандайда бір маңызды үғым алғаш енгізіліп жатса, онда оған сәйкес ассоциациялар оқушылар санына берік енеді. Келесі әсерлер босаңдау болуы және алғаш берілген үғымдарды жоя алмауы мүмкін».

Бүрыштық қабылдайтын мәндер жиынының кеңеюі басқышында синус және косинусының «жаңа» анықтамасын енгізу үшін біз шеңберді пайдаланганымызға қарамастан және бір рет тікбүрышты үшбүрышпен сандық шеңбер арасындағы байланысты айқындау қажет.

Мектеп оқулықтарында Бұл фактіге неліктен айтарлықтай көңіл бөлінбейтінін ескертеміз (әртүрлі мектеп оқушыларында «Тригонометриялық функциялар» тақырыбын баяндаудың талдау тарауына қараңыз), сондықтан мүғалім осы басқышта триғонометриялық функцияларды енгізуде келесі моменттердің айтылуына назар аудару керек.

Тікбүрышты декарттық координаттарды орналасқан бірлік радиустағы сандық шеңберді қарастырамыз.

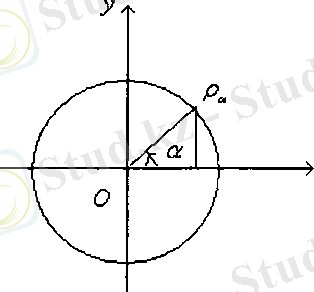
$C:\Users\deettt\AppData\Local\Temp\FineReader11\media\image4.png$

Сурет 1

ОХ өсінен оң бағытта 0<α<90° болатындай α бұрышты қоямыз. Шеңберде алынған нүктені Рα - нүктесінде О х -осіне перпендикуляр жүргіземіз және М нүктені аламыз. Алынған ОМ Рα тікбүрышты үшбүрышты қарастырамыз. Анықтама бойынша, зіпа МРα/ОРα қатынасына тең, бірақ шеңбердің ОРа радиусы 1 - ге тең. Демек, Sinα = МРα. Дэл осылай, cosα = ОМ. Тікбүрыштыдекарттық координат жүйесінде ОМ ұзындығыБұл Рα нүктесінің абциссасы, ал МРα ұзындығы оның ординатасы. Сонымен α бүрышының синусы мен косинусы Рα нүктенің ординатасы және абциссасымен анықталады, Бұл тікбүрышты декарттық координат жүйесінде жүмыс істеуге қолайлы.

Сандық шеңбермен жүмыс істеуде бірлік шеңбердің доғасының ұзындығы, доғаға тірелетін центрлік бүрышпен оңай өрнектелетін фактын біз алдын меңгердік, сондықтан, Рα нүктесін басқа тэсілмен де қүруға болады берілген үзындықтағы доганы салумен. Доғаның ұзындығы барлық уақытта нақты сан болғандықтан, демек, бүрыштық аргументті тригонометриялық функцияларға оңай өтуге болады. Енді α бүрышына қойылған шектеулерге қайтайық. α бүрышы 0° тан 90° дейінгі аралыққа тиісті, демек, доға ұзындығы 0 мен π/2арасында жатады. Геометриялық интерпретацияны пайдаланып, Бұл анықтамаларды кез келген бүрыш және сандарға таратуға болады.

Тангенс және котангенс ұғымдарын екі түрге келтіріп шығаруға болады. Синустың косинусқа (косинустың синусқа) қатынасы ретінде және шеңберге ((1; 0), (0; 1) ) нүктедегі жанаманың және ОРα түзудің қиылысу нүктесінің ординатасы (абсциссасы) ретінде. [16-24]

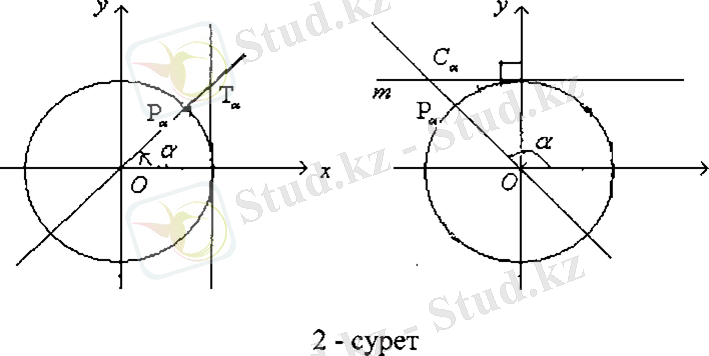
Сурет 2

Жалпы айтқанда, синус пен косинус функцияларын анықтап, оларды сандық шеңберге тангенс және котангенс ұғымдарын енгізу үшін қүрал ретінде қарастыруға біз мүқтаж емеспіз. Осы моделмен жүмыс істеуді алғандығымыздан, тек геометриялық анықтаманы ғана пайдаланып, тангенс және котангенс функцияларын анықтауды көрсету жөн болады. («α бүрыштың тангенсі - Бұл синус α-ға қатынасы» сөйлемдері анықтама болып табылмайтынын олар қасиеттер екендігін ескереміз) .

Екінші жанасуды пайдалану тригонометриялық функцияларды үйрену басқышында ғана емес, сондай-ақ тригонометриялық теңдеулерді және теңсіздіктерді шешу басқышында да көмектеседі. Сондықтан дэл осы екінші жанасуды пайдалану мақсатқа сай, ал тангенс α-синус α -тың косинус α -ға қатынасы анықтамасын қасиет ретінде қарастыру жөн.

Сонымен, біз барлық тригонометриялық функциялар үғымын енгіздік (бағдарламамен көзделген) .

Бірақ, графиктерді қүру және зерттеуге өтуге алдын, оқушыларда келесі дағдылардың болуын бақылау қажет:

•«Басты» нүктелерді барлық тригонометриялардың мәндерін табу.

•Қарапайым тригонометриялық теңдеулерді және теңсіздіктерді шешу.

•Тригонометриялық функциялардың берілген нүктелердегі мәндерін анықтау.

•Негізгі тригонометриялық тепе-теңдікті және келтіру формулаларын пайдаланумен өрнектерді ықшамдау.

•Бір тригонометриялық функцияның берілген мәндері бойынша қалған барлық тригонометриялық функциялардың мэнін табу.

Жоғарыда аталған дағдыларды игеріп, оқушылар тригонометриялық функциялардың графиктерін ілгері күру және зерттеу үшін жеткілікті құралдар арсеналын алады.

Графиктерді құру және функцияларды зерттеу жұмысы екі тэсілмен жүргізілуі мүмкін:

1) Алдымен нүктелер бойынша график құралады, содан соң графиктік интерпретация көмегінде функцияның барлық қасиеттері зерттеледі.

2) Графикті кұру функцияны зерттеуден соң жүргізіледі, ал қасиеттер туралы көрнекті түсініктерді оқушылар функцияның сандық шеңбердегі өзгеруін талдаудан алады.

Екінші жанасуды қолданған мақсатқа сай Бұл жанасуда, біріншіден, тригонометриялық функцияның барлық қасиеттері екі моделде де бейнеленеді (сандық шеңберде де, графикте де), ал екіншіден, бұл туынды көмкгінде функцияларды зерттеу және графиктерді құруды әрі қарай оқыту үшін жақсы дайындық жұмысы болып табылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.