Жиын уғымы

1.Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3

2 Негізгі бөлім ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5
2.1 Жиын уғымы. Жиынның элементтері ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
2.2 Жиын элементтерінің арасындағы қатыстар ... ... ... ... ... ... ... ... ... ... .14
2.2 Жиындармен жүргізілетін сабақ жоспарлары ... ... ... ... ... ... ... ... ... ... 23

3. Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..26

Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 27

Бастауыш класстарда математика оқытудың мақсаттары, міндеттері мен мазмұны.
1. Бастауышда жұмыс істеуде орта мектепте математика оқытуда жоспарланған жалпы мәселелерді есепке алу және бұл мәселелерді шешудегі бастауыш білімнің рөлін дұрыс бағалай білу.
2. Орта мектеп математика жоспарына қатысты көптеген мәселелер бастауыштың өзінде тиісті дәрежеде берік үйретілуі керек, яғни олар оқушылар санасында өмір бойы сақталып қалатын болсын, ал кейбір мәселелер жоғары сыныпта толық түрде өтілуіне қарай, бастапқы ұғымдар, дайындық есебінде қаралады. Немесе біліктілік пен дағқыларды қалыптастыру процессінде пікірлеу қабілетін арттыру мақсатында қаралады.
Міндеттері
1. Оқушыларда саналы және берік (автомат түрде) есептеу біліктілігін қалыптастыру

1. Әбілқасымова А.Е. және басқалар. Математиканы оқытудың теориясы мен әдістемесі. А., Білім, 1998ж. 202 бет
2. Әбілқасымова А.Е Математикадан дидактикалық тапсырмалар жинағы А., Қазақ университеті баспасы. 1991ж. 71 бет
3. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. М., Просвещение. 1984, 335 стр.
4. Оспанов Т.Қ. Бастауыш кластарда математиканы оқыту методикасы. А., Мектеп, 1997ж. 160 бет.
5. Рахымбеков Д. Кенешев Ә. Математикалық ұғымдарды оқыту. Жезқазған., ЖУ. 1997 -61 бет
6. 1,2,3,4 кластарға арналған Математика оқулықтары
7. Оспанов Т.Қ., Қурмалина Ш.Х. Математиканың бастауыш курсын оқыту әдістемесі ІІ болім А. Республикалық баспа кабинеті 1996
8. Абдрахманова К. Төменгі жастағыларды оқыту ерекшеліктері // Бастауыш мектеп. – 1989. - №9. - 10-12 бет.
9. Бантова М.А. Бастауыш кластарда математиканы оқыту методикасы. - Алматы: Мектеп, 1978. - 125 бет.
10. Бидосов Ә. Математиканы оқыту методикасы. - Алматы: Мектеп, 1981. - 145 бет.
11. Делман И.Я. Матаматиканың логикалық бет ашары. - Алматы, 1970. – 265 б.
12. Елубаев Е. Есепті қалай шығару керек. - Алматы: Мектеп, 1984. - 260 бет.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Мазмұны

1.Кіріспе ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... .3

2 Негізгі
бөлім ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ..5
2.1 Жиын уғымы. Жиынның
элементтері ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
2.2 Жиын элементтерінің арасындағы
қатыстар ... ... ... ... ... ... ... ... ... ... ..14
2.2 Жиындармен жүргізілетін сабақ
жоспарлары ... ... ... ... ... ... . ... ... ... ...23

3.
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... 26

Пайдаланылған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... 27

1 Кіріспе
Бастауыш класстарда математика оқытудың мақсаттары, міндеттері мен
мазмұны.
1. Бастауышда жұмыс істеуде орта мектепте математика оқытуда
жоспарланған жалпы мәселелерді есепке алу және бұл мәселелерді шешудегі
бастауыш білімнің рөлін дұрыс бағалай білу.
2. Орта мектеп математика жоспарына қатысты көптеген мәселелер
бастауыштың өзінде тиісті дәрежеде берік үйретілуі керек, яғни олар
оқушылар санасында өмір бойы сақталып қалатын болсын, ал кейбір мәселелер
жоғары сыныпта толық түрде өтілуіне қарай, бастапқы ұғымдар, дайындық
есебінде қаралады. Немесе біліктілік пен дағқыларды қалыптастыру
процессінде пікірлеу қабілетін арттыру мақсатында қаралады.
Міндеттері
1. Оқушыларда саналы және берік (автомат түрде) есептеу біліктілігін
қалыптастыру
2. Оқушыларға үйренген білім, дағды және біліктіліктерін әр түрлі
жағдайларда қолдануға үйрету.
3. Оқушыларда қисынды (логикалық) пікірлеу қабілетін қалыптастыру.
4. Оқушыларға толық, нақты, қысқа да нұсқа математикалық сөйлеуді
үйрету
5. Оқушыларды еңбекке баулу, сана тәртіптілігі, еңбекті нақтылай
ұйымдастыру, пікірді бір орынға топтау және нақтылауға үйрету.
Мақсаттары
1. Білім беру
2. Тәрбиелеу
3. Өмірлік -практикалық білім - дағды дарыту
1. Математиканы оқытудың білімдін мақсаты барлық оқушыларды математика
ғылыми негіздері туралы жүйелі білімдермен және оларды толық, сапалы да
берік игеруге қажетті біліктіліктермен, дағдылармен қаруландыру болып
табылады.
Осындай білім алу нәтижесінде оқушылардың ақыл ойы дамиды.
2. Тәрбиелік мақсат - математиканы үйрету барысында оқушыларды жан-
жақты тәрбиелеуге мүмкіндік беретін барлық қолайлы сәттерді пайдалану болып
табылады. Тәрбиенің кейбір негізгі түрлері:
а) оқушыларда ғылыми дүние танымын қалыптастыру (Тарихи -
математикалық мағлуматтар көмегімен)
б) Шәкірттерде озық моралдық қасиеттерді қалыптастыру (саналы тәртіп,
белсенділік, қиындықты жеңе білу бастаған істі аяғына дейін жеткізе білу,
табандылық адалдық, жауапкершілік т.б.)
в) Математика сабағында - патриотизм және интернационализм рухында
тәрбилеу (Ал-Фараби, әл-Хорезми т.б.)
г) Эстетикалық тәрбие (әдемілік) фигуралардың қасиеттері, симметрия.
Ең әсем шешуін табу.
3. Өмірлік -практикалық мақсат
а) өмірлік -практиканың қарапайым есептерін шешуге физика, химия,
сызу, ақпараттану т.б. пәндерді оқып үйренуге пайдалану білу
б) математикалық құралдармен аспаптарды пайдалана алу
в) шәкірттердің өз бетінше білім алуын қамтамасыз ету
г) политехникалық оқуды жүзеге асыруға қолтабыс тигізу

2 Негізгі бөлім

Жиын уғымы. Жиынның элементтері
Жиын ұғымы математикада негізгі (анықтауға болмайтын, бастапқы) ұғым
болып саналады. Сондықтан оны тек мысылдармен ғана түсіндіруге болады.
Мысалы, қайсыбір класс оқушыларының жиыны туралы, Әлемдегі планеталар жиыны
туралы айтуға болады. Жиын сөзі математикада жиынтық, класс, жинақ,
коллекция деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын
сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықты
бір ғана нәрсе болуы немесе бірде-бір нәрсе болмауы мүмкін.
Жиын құратын кез-келген нәрселер (адамдар, үйлер, кітаптар, елдер,
геометриялық фигуралар, сандар т. б.) оның элементтері деп аталады. Мысалы,
3 саны - бір таңбалы натурал сандар жиынының элементі. Жиын мен оның
элементтерінің арасындағы элементті болады деген байланысты тиісті
сөзінің көмегімен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал
сандар жиынына тиісті деп айтуға болады.
Соңғы сөйлемде символдың көмегімен қысқаша жазуға болады: 3ÏА. Бұл
жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды
латын алфавитінің бас әріптерімен белгілейді), ал Îбелгісі тиісті сөзін
алмастырады.
Жалпы аÎА жазуы а нәрсесі А жиынының элементті, немесе а нәрсесі А
жиынына тиісті, немесе А жиынында а элементі бар деп оқылады. аÏА жазуын
а нәрсесі А жиынына тиісті емес, немесе А жиынында а элементті жоқ,
немесе а нәрсесі А жиынының элементі емес деп оқуға болады.
Жиын элементтерінің саны шектеулі де, шектеусіз болуы мүмкін. Мысалы,
қайсыбір педучилище оқушыларының жиының элементтерінің саны шектеулі, ал
түзудегі нүктелер жиыны шектеусіз.
Жиын ұғымы және онымен байланысты басқа да ұғымдар математиканы алғаш
оқытудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда
жиын термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде
пайдаланылады, ал бір қатар эксперимент кітаптарда жиын ұғымы
символикасымен қоса айқын түрде пайдалалынылады. Сан, натурал сандарды қосу
және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты
маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық -
жиындық негізде жүзеге асады.
Жиындардың жазылуы мен оның берілу тәсілдері
Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес
екендігін айта алатын болсақ, онда жиын берілген деп саналады.
Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады.
Егер де а, b, c, d - әр түрлі нәрселердің белгіленулері болса, онда осы
нәрселердің жиынын А={ а, b, c, d } түрінде жазып, оны А жиыны а, b, c, d
элементтерінен тұрады деп оқиды.
Әрбір нәрсе жиынға тек бір рет қана енеді. Мысалы, 32 545 882 санының
әр түрлі цифрларынан тұратын жиын {3, 2, 5, 4, 8}, ал есеп деген сөздегі
әр түрлі әріптер жиыны {e, c, п} түрінде жазылады.
Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ
қасиетін атау болып табылады. Мұндай қасиетті cипаттамалық қасиет деп
атайды. Мысалға, 7-ден кем натурал сандардың А жиынын қарастырайық. Бұл
жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда,
олардың натурал және 7-ден кіші сан болуы аталып отыр. Қарастырылып
отырған А жиынының элементтерін атап шығу қиындыққа түспейді: А={1, 2, 3
,4, 5, 6}
Жиынның осылай берілу тәсілі математикада жиі қолданылады. Мысалға
радиусы r, центрі О болатын шеңбердің центрі О және радиусы r болатын
шеңбер деп жазықтықтың О нүктесінен r қашықтықта жататын нүктелер жиынын
атайды деген анықтамасын еске түсірейік. О-дан r қашықтықта және бір
жазықтықта жату - центрі О және радиусы r болатын шеңбердің барлық
нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде бір
нүкте ие бола алмайды.
Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға
болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады.
Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын
элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы, 7-ден кіші
натурал сандар жиыны А былайша жазылады:
А={xx- натурал сан, x7}
Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін
атап шығу, не оның элементтеріне тән қасиетті көрсету керек. Екінші тәсіл
біріншіге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның
элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын
элементтерінің ортақ қасиетін жиын шектеулі болғанда ғана мү мкін, ал жиын
элементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да
көрсетуге болады.
Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып
жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы
белгілеп мына түрде
N= {1, 2, 3, 4, ...} жазуға болады.
Әрине жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда
ғана осы түрде жазуға болады.
Барлық натурал сандардан және нольден тұратын жиынды N0 арқылы
белгілеп, былай жазады:
N0={1, 2, 3, 4, ...}
Бұл жиынды оң бүтін сандар жиыны деп атайды.
Барлық бүтін сандар жиынын Z әрпі арқылы белгілеу келісілген: Z={...,
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}
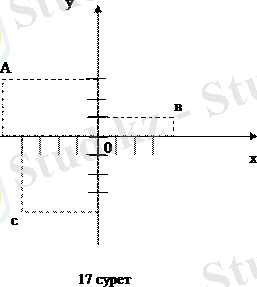
сан болады: -5, 3.

Жиындардың декарттық көбейтіндісі
Бізге Алматыдан және Астанадан, Стамбул, Москва және Пекин қалаларына
барлық мүмкін маршруттардың жиынын құру керек болсын. Бұл маршруттар:
Алматы-Стамбул, Алматы-Москва, Алматы-Пекин, Астана-Стамбул, Астана-Москва,
Астана-Пекин.
Алматы және Астана қалаларынан тұратын жиынды Х арқылы, ал Стамбул,
Москва, Пекин қалаларынан тұратын жиынды У арқылы белгілейік, яғни
Х={Алматы, Астана}, У={Стамбул, Москва, Пекин}. Онда маршруттардың жиыны
(18-сурет) бірінші компоненті Х жиынының, ал екінші компоненті У жиынының
элементі болатын жұптардың жиыны екенін көреміз. Олай болса, маршруттардың
жиынын былайша жазуға болады: {Алматы-Стамбул, Алматы-Москва, Алматы-
Пекин, Астана-Стамбул, Астана-Москва, Астана-Пекин}.

Осылайша құрылған жұптар жиыны Х және У жиындарының декарттық
көбейтіндісі деп аталады. Жалпы, Х және У жиындарының декарттық
көбейтіндісі деп бірінші компоненті хÎХ, ал екінші компоненті уÎУ болатын
барлық х, ужұптарының жиынын айтады.
Х және У жиындарының декарттық көбейтіндісін Х´У арқылы белгілейді,
яғни
Х´У={х, у ïхÎХ, уÎУ}.
Тағы да мысал келтірейік. Х={1, 2, 3, 4} және У={а, в, с} жиындарының
декарттық көбейтіндісін табу керек болсын. Анықтамасы бойынша ол мынадай
жұптардан тұрады: Х´У={1, а, 1, в, 1, с, 2, а, 2, в, 2, с, 3,
а, 3, в, 3, с, 4, а, 4, в, 4, с}.
Осы декарттық көбейтіндіні таблица арқылы жазған қолайлы:
Х´У жиынының әрбір элементі таблицаның сәйкес жолы мен бағанасының
қиылысқан клеткасына жазылады. Олай болса, таблицаның клеткаларының жиыны
Х={1, 2, 3, 4} және У={а, в, с} жиындарының декарттық көбейтіндісін береді
екен.
Сәйкестіктер
Жиындар арасындағы сәйкестік
Қайсыбір класс оқушылары Арманға, Еділге, Қайратқа, Динаға, Талғатқа
және Сәулеге: ²Сендер футбол, волейбол, жүзу, гимнастика және теннис сияқты
спорт түрлерімен шұғылданасыңдар ма?²деп сұрақ қойылған. Олардың жауаптары
кестеге орналастырылды.
ФутболВолейболЖүзуГимнастикаТе ннис
Арман
Еділ
Қайрат
Дина
Талғат
Сәуле

Кестеден Арманның волейболмен және тенниспен шұғылданатынын, Динаның
волейболмен шұғылданатыны, Талғаттың спорттың ешбір түріне қатыспайтындығы
көрініп тұр. Сонымен қатар, сұралған оқушылардың арасында спорт түрінің ең
әйгілісі волейбол екені, ал гимнастиканың оларды қызықтырмайтындығы да
таблицада көрініп тұр.
Бұл мысалда екі жиын берілген: оқушылар аттарының жиыны және спорт
түрлері аттарының жиыны. Бірінші жиынды Х, ал екінші жиынды У арқылы
белгілейік. Сонда Х={Арман, Еділ, Қайрат, Дина, Талғат, Сәуле}, ал
У={футбол, волейбол, жүзу, гимнастика, теннис} деп жазуға болады. ²Спорттың
қайсыбір түрімен шұғылдану² деген сөз арқылы осы екі жиын элементтерінің
арасында қандай да бір байланыс тағайындалып отыр. Осындай байланыс
математикада сәйкестік деп аталады. Таблицада бұл сәйкестілік штрихталған
клеткалармен көрсетілген. Осы таблицадағы барлық клеткалардың жиыны Х және
У жиындарының декарттық көбейтіндісі болатындығы белгілі. әрбір штрихталған
клетка осы жиынға тиісті болғандықтан, штрихталған клеткалар жиыны
декарттық көбейтінді Х´У жиынының ішкі жиыны болады. Сонымен, Х және У
жиындарының арасындағы сәйкестікті біз үш жиынды пайдаланып тағайындадық:
оқушылар аттарының Х жиыны, спорт түрлері аттарының У жиыны және Х´У
декарттық көбейтіндінің ішкі жиыны.
Декарттық көбейтіндінің ішкі жиынын G әрпімен белгілеп, оның
элементтерін атап шығайық: G={Арман, волейбол, Арман, теннис, Еділ,
футбол, Еділ, волейбол, Еділ, теннис, Қайрат, футбол, Қайрат,
жүзу, Дина, волейбол, Сәуле, волейбол, Сәуле, теннис}.
Жалпы, Х және У жиындарының арасындағы сәйкестік деп жиындар үштігі
аталады: Х жиыны, У жиыны және Х´У декарттық көбейтіндінің қандай да ішкі
жиыны G. Х - жиыны сәйкестіктің шығу жиыны У жиыны сәйкестіктін келу жиыны,
ал GÌ Х´У жиыны осы сәйкестіктің графигі деп аталады.
Жиындар арасындағы сәйкестікті R,P,Q,S,T әріптермен белгілеуге
келісейік. Осы келісімді пайдаланып, жоғарыдағы мысал туралы былай деуге
болады: біз оқушылар аттарының жиыны Х (шығу жиыны) және спорт түрлері
аттарының жиыны У (келу жиыны) арасында R сәйкестігін анықтадық, мұндағы R
- ²оқушы хÎХ спорттың уÎУ түрімен айналысады².
Х´У декарттық көбейтінді хÎХ уÎУ болатын барлық мүмкін болатын
х;ужұптардан турады. Егер Х және У жиындары арасындағы сәйкестік R, ал G
жиыны оның графигі және х;у ÎG екендігі белгілі болса, онда R сәйкестікте
у элементі х элементіне сәйкес немесе х және у элементтерінің арасында R
сәйкестігі орындалады дейді, және оны хRу түрінде жазады. хRу жазуын былай
оқиды: ²R сәйкестікте у элементі х элементіне сәйкес болады².
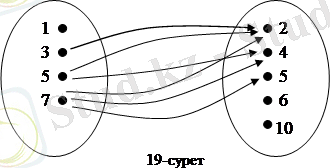
Мысалы, егер Х={1, 3, 5, 7}, У={2, 4, 6, 8, 10}, ал Х және У
арасындағы қандайда бір R сәйкестігінің графигі G={3, 2, 5, 2, 5, 4,
7, 2, 7, 4, 7, 6} болса, онда, мәселен G жиынының 3, 2жұп туралы
3ÎХ және 2ÎУ сандарының арасында R сәйкестілігі орындалады деп немесе R
сәйкестігінде 2 саны 3 санына сәйкес келеді деп айтуға болады және оны
былай жазуға болады: 3R2.
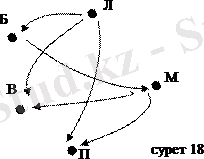
Осы мысалдағы R сәйкестігіне сөзбен айтқанда мынадай нақтылы мағына
беруге боладв: ²Х жиынынан алынған х саны У жиынынан алынған у санынан
үлкен². Сонда, 3R2 жазуын былай оқуға болады: ²Х жиынынан алынған 3 саны У
жиынынан алынған 2 санынан үлкен². ²х саны у санынан үлкен² деген Х={1, 3,
5, 7} және У={2, 4, 6, 8, 10} жиындарының арасындағы R сәйкестігін чертеж
арқылы көрнекті түрде елестетуге болады. Ол үшін берілген жиындарының Эйлер-
Венн диаграммаларын құрып, олардың элементтерін нүктелер арқылы
кескіндейміз. Сонаң соң сәйкестіктің графигіне тиісті әрбір х,ужұптарының
элементтерін басы х элементін кескіндейтін нүктеде, ал соны у элементін
кескіндейтін нүктеде болатын стрелкамен қосамыз (19-сурет). Сонда шыққан
чертежді R сәйкестігінің графы деп атайды.
Егер Х және У жиындарының арасында қандайда бір R сәйкестігі
тағайындалған болса, онда Х шығу жиынының элементіне а) У келу жиынының
бірнеше (тіпті шектеусіз көп) элементтерінің сәйкес келуі;
б) У жиынының тек бір ғана элементі сәйкес келуі;
в) У жиынының бірде-бір элементі сәйкес келмеуі мүмкін.
Шынында да егер R Х={1, 3, 5, 7} және У={2, 4, 6, 8, 10} жиындарының
арасындағы ²х саны у санынан үлкен² сәйкестік болса, онда 7ÎХ элементіне У
жиынының үш элементі сәйкес келеді: 7R2, 7R4, 7R6. Графта (19-сурет) 7
санын өрнектейтін нүктеден үш стрелка шығатындығы көрініп тұр. 3ÎХ
элементіне У жиынын тек қана бір элементі 2 сәйкес келеді. Графта 3 санын
өрнектейтін нүктеден бір ғана стрелка шығады. Ал 1ÎХ элементіне У жиынының
бірде-бір элементі сәйкес келмейді, сондықтан да графта оны өрнектейтін
нүктеден ешқандай стрелка шықпайды.
Келу У жиынының элементі шығу Х жиынының бірнеше элементтеріне, не тек
бір элементіне сәйкес келуі, немесе бірде-бір элементіне сәйкес келмеуі
мүмкін. Бұл ескертуді түсіндіретін мысалдарды өздеріңіз оңай-ақ келтіре
аласыз.
Жиындар арасындағы сәйкестік ұғымы математикадағы негізгі ұғымдарының
қатарына жатады. Олай болатын себебі: бұл ұғым математикадағы функция және
бейнелеу сияқты аса маңызды ұғымдарды анықтаудың негізі болып табылады.
Сонымен қатар арасындағы кез келген ғылымда объектілердің өздері ғана емес,
олардың арасындағы байланыстар да зерттеледі. Мысалы, географияда қалалар
жиыны Х және елдер жиыны У арасында ²х қаласы у у еліне қарайды² деген
сәйкестік қарастырылады. Қазақ тілінде ²х сөзі у сөз табына жатады ² деген
сияқты әр түрлі сөздер жиыны мен сөз таптары жиынының арасындағы сәйкестік
кеңінен таралған. Физикада: ²х денесінің массасы у-ке тең²; химияда: ²х
затының формуласы у болады².
Сәйкестік графигі
Х және У жиындарының арасындағы R сәйкестігінің графигі Х´У декарттық
көбейтіндінің ішкі жиыны болатындықтан, ХУдекарттық көбейтіндінің
графигі туралы айтылғандардың бәрі R сәйкестігінің графигі үшін де тура
болады.
Мысалы, Х={а, в, с}, ал У={m,n} болсын және G={а,m, в, m, с,n,
в,n}- берілген Х және У жиындарының арасындағы қайсыбір R сәйкестігінің
графигі болсын. Онда - суретте көрсетілген нүктелердің жиыны берілген R
сәйкестігінің графигін кескіндейді.
Декарттық көбейтінді сияқты Х және У жиындарының арасындағы R
сәйкестігінің графигін де тік бұрышты координаталар системасында нүктелер
жиыны ретінде кескіндеуге болады. Мысалы, егер Х={5, 10}, У={1, 2, 3} және
G={5, 1, 10, 1, 10, 2}-Х және У жиындарының арасындағы қайсыбір R
сәйкестігінің графигі болса, онда координаттық жазықтықта координаталары G
жиынының жұптары болатын барлық нүктелерді салатын болсақ, ол R
сәйкестігінің графигі болады (20-сурет).

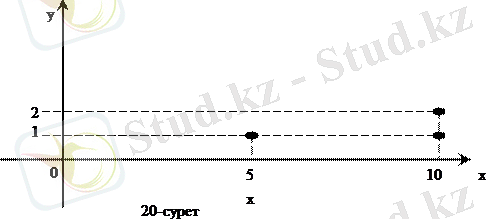
Х=У=Zжәне R-Х және у жиындарының арасындағы ²х саны у санынан 3
саннына артық² деген сәйкестік болсын. Тік бұрышты координаталар
системасында осы сәйкестіктің графигін салайық. Графикке тиісті жұптардың
жиыны шектеусіз, олай болса, біз координаттық жазықтықта абсциссасы бүтін
сан, ал ординатасы абсциссасынан 3 бірлікке кем болатын нүктелердің
шектеусіз жиынын аламыз. Біз графиктің тек қайсыбір бөлігін ғана құра
аламыз, мысалы, мынадай 1, -2, 0, -3, 5, 2, 10, 7, -3, -6
нүктелерді (21-сурет). Осы нүктелердің барлығы бір түзу бойында жатады.

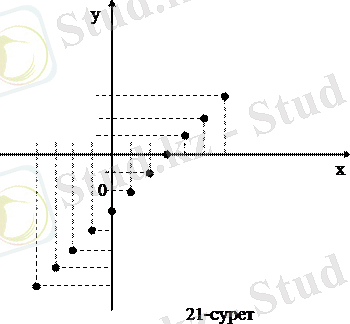
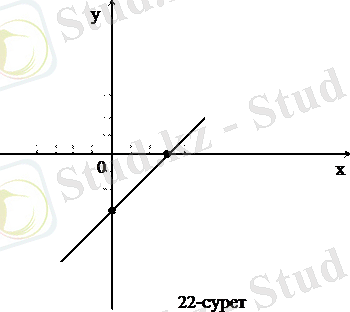
Егер Х=У=R, ал сәйкестік алдағы мысалдағыдай болса, онда ол
сәйкестіліктің графигі түзу сызық болады (22-сурет).

Кері сәйкестік
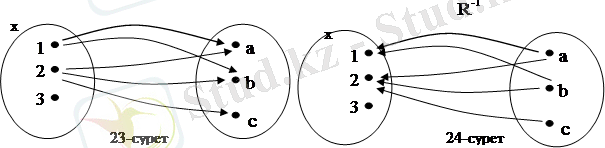23-суретте Х={1, 2, 3} және У={а, в, с} жиындарының арасындағы
қайсыбір R сәйкестігінің графы берілген. Бұл жерде 1ÎХ элементіне У
жиынының а және в элементтері сәйкес, яғни 1Rа, 1Rв, 2Rа, 2Rв, 2Rс екенін
көреміз.
Біздің мысалымызда Х және У жиындарының арасындағы R сәйкестігінің
графигі мынадай: {1, а, 1, в, 2, а, 2, в, 2, с}, ал R
сәйкестігіне кері У және Х жиындарының арасындағы R-1 сәйкестігінің графигі
мынадай жиын болады: {а, 1, в, 1, а, 2, в, 2, с, 2}, яғни егер R
сәйкестігінің графигіндегі оған тиісті әрбір жұптың компоненттерінің
орындарын ауыстырса, онда R-1 сәйкестігінің графигі келіп шығады.
R және R-1 сәйкестіктерін тік бұрышты координаталар системасында
кескіндегенде олардың графиктері өзара қандай байланыста болатынын
анықтайық. Х={-3, -2, -1, 0} және У={0, 1, -2} жиындарының арасындағы ²хÎХ
саны уÎУ санынан аз² деген R сәйкестік бар болсын. Сонда R сәйкестігінің
графигі {-3, 0, -3, 1, -3, -2, -2, 0, -2, 1, -1, 0, -1, 1,
0, 1} болады да, тік бұрышты координаталар системасында 25-суретте
көрсетілген сегіз нүкте болады.

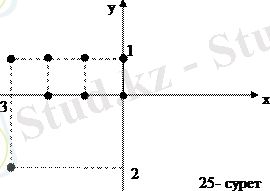
Берілген сәйкестікке кері R-1 сәйкестігінің графигі мынадай болады:
{0, -3, 1,-3 , -2, -3, 0, -2, 1, -2, 0, -1, 1,-1, 1, 0}.
Оның координаттық жазықтықтағы кескінін сіздер 26-суреттен көріп
отырсыздар.
R және R-1 сәйкестіктерінің графиктерін бір чертежге салайық (27-
сурет). Енді R және R-1 сәйкестіктерінің графиктері бірінші және үшінші
координаталық бұрыштардың биссектрисасына қарағанда симметриялы екендігіне
оңай-ақ көз жеткізуге болады

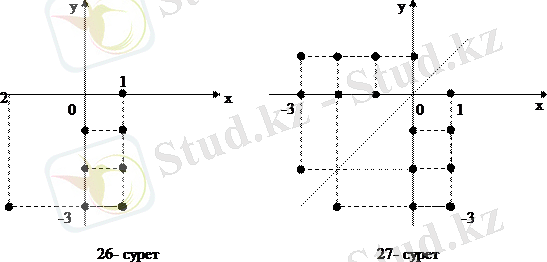
Біздің мысалымызда У және Х жиындарының арасындағы R-1 сәйкестігін
²уÎУ саны хÎХ санынан көп² деген сөйлеммен білдіруге болатындығын
ескертеміз.
Сонымен, егер Х және У жиындарының арасындағы сәйкестік R болса, онда
У және Х жиындарының арасындағы уR-1х, уÎУ, хÎХ болатындай R-1сәйкестігі
хRу болғанда және тек сонда ғана R сәйкестігіне кері сәйкестік болып
табылады.
Кері сәйкестік ұғымын біз жиі пайдаланамыз. Бірнеше мысал келтірейік.
Х - әр түрлі қазақ сөздерінің жиыны, ал У - қазақ тіліндегі сөз
таптарының жиыны болсын. Осы жиындардың арасында ²х сөзі у сөз табына
жатады² деген сәйкестік бар (мысалы, ²үй²сөзі - зат есім, ²жаз² - сөз
-етістік т.с.с.). Осы сәйкестікке кері У және Х жиындарының арасындағы
сәйкестік ²у сөз табына х сөзі жатады² (мысалы, зат есімге ²үй²сөзі,
етістікке ²жаз² сөзі жатады деп айтамыз) түрінде айтылатын болады.
Егер Х - әлемдегі мемлекеттер жиыны, ал У - олардың астаналарының
жиыны болатын болса, онда Х және У арасындағы R сәйкестігі ²х мемлекетінің
астанасы у² деген түрде болуы мүмкін. Онда У және Х жиындарының арасындағы
R-1 сәйкестігін біз ²у қаласы - х мемлекетінің астанасы² деген түрде
тұжырымдауымыз керек.
Сәйкестіктің жеке түрлері

2.2 Жиын элементтерінің арасындағы қатыстар
Біз екі жиын элементтерінің арасындағы әр түрлі сәйкестік болатынын
анықтадық. Бірақ әр түрлі байланыстар мен қатыстар бір ғана жиын
элементтерінің арасында да болады.
Мысалы, әлемдегі барлық елдер жиынын қарастырсақ, онда елдер арасында
мынадай қатыстар белгілеуімізге болады. ²х елінің халқы у елінің халқынан
көп, х және у елдері шекаралас² т.с.с. Ал адамдар арасындағы қатыстар
түрлері қаншама десеңізші: ²х деген кісі у деген кісінің әкесі², ²х деген
кісі у деген кісіні оқытады², ²х және у деген кісілер - достар², ²х деген
кісі у-тің бауыры² деген сияқты адамдар арасындағы мүмкін болатын қатыс
түрлерін сіздер оп-оңай жалғастыра аласыздар.
Математикада да бір ғана жиынның элемнттері арасындағы қатыстар біздің
назарымызды аударады. Натурал сандар жиынында біз мынадай қатыстарды
қарастырамыз. ²х саны у санына тең², ²х саны у санынан артық², ²х саны у
санына бөлінеді² т.с.с. Геометрияда ²х фигурасы у фигурасына конгруфнтті²,
²х фигурасы у фигураның бөлігі², ²х фигурасы у фигурасына ұқсас² т.с.с.
қатыстарды оқимыз. Жалпы, Х жиындағы қатыс деп осы жиын элементтерінің
арасындағы сәйкестікті айтады. (Қатыс терминін математикада екі санның
бөліндісі үшін қолданылатын ²қатынас²терминімен шатастырмау керек).
R қатысын анықтап беру үшін екі жиынды. Х жиынын және хÎХ, уÎУ болатын
х; ужұптарының G жиынын (GÌХ´Х) қарастыру керек. G жиынын Х жиынындағы R
қатысының графигі деп атайды.
Қатыс сәйкестіктің дербес түрі болғандықтан, бұрынғы сәйкестік және
оның графигі туралы айтылғандардың барлығын қатыс туралы да айтуға
болады.осы айтылғандарды нақты мысалдармен сипаттайық.
1-мысал. Х= {1, 2, 3, 4} жиынының элементтері арасында ²х саны у
санынан кіші², әрі х,уÎХ, деген R қатысы орындалатын болсын. Х жиынының R
қатысында болатын элементтерінің барлық жұптарын атап шықсақ, онда осы
қатыстың графигін шығарып аламыз:
G= { 1, 2, 1, 3, 1, 4, 2, 3, 2, 4, 3, 4}.
Көрсетілген R қатысын граф арқылы кескіндеуге болады. Ол үшін Х
жиынының элементтерін нүктелер арқылы белгілеп және х санынан у сандарына
қарай стрелка жүргіземіз, мұнда у саны х санынан үлкен (28-сурет). Сонда
берілген қатыстың графындағы әрбір стрелка ²кіші² деген сөзді алмастырады:
1 саны 2-ден кіші, 2 саны 3-тен кіші т.с.с.
2-мысал. Х= {1, 2, 3, 4} жиыны элементтерінің арасында ²х саны у
санына еселі², х, уÎХ деген Sқатысы да орындалсын. S қатысының графын
құрайық. Барлық сан 1-ге еселі болғандықтан, Х жиынының әрбір санынан1-ге
қарай стрелка жүргіземіз: кез келген сан өзіне бөлінеді, ендеше, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.