Сүт өнімі туралы мәлімет

Пән: Ет, сүт, шарап өнімдері
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

Кіріспе

Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан ір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.

Математикалық есептерді шешкенде мектеп оқушыларында логикалық ойлау қабілеті мен олардың өнертапқыштық қасиеттері дамитындығы белгілі. Жоғарғы сынып оқушыларының математика пәнін оқу кезінде олардың төмендегі қасиеттері дамитындығы белгілі:

1. Берілген есеп белгілі бір есептердің класына жататындығын ұғыну; Есепті әртүрлі әдістермен шешіп және ол әдістердің жеңіл және қиын жақтарын ескере отырып, оның «керемет» шешу жолын анықтау. Есептің шығарылу әдістерін салыстыру және талдау арқылы, оқушылар өздерінің алған білімдерін терңдетуге және нықтауға мүмкіндік алады. Сондықтан бір типтегі есептердің бірнешеуін шешкеннен, бір есепті бірнеше әдіспен шешу тиімділігін ұғынады.

2. Өздігінше бірнеше белгілі әдістерді комбинациялайды.

3. Есепті шешу кезінде ең кем дегенде жаңаша бір әдіс алу мүмкіндігі дамиды.

Зерттеудің өзектілігі: Оқушылардың творчествалық дамуы үшін қиын және стандартты емес есептерді шешу өте маңызды. Қиын математикалық есептерді шешу үшін, оқушылардың мұндай есептерді шешуде тәжербиесінің, оларды шешу әдістері мен оларға түрлендірулер пайдалана білу қабілеттіліктерін мол болуы талап етеді. Стандартты емес есептер - нақты бір шешу алгоритмі жоқ есептер. Сондықтан мұндай есептерді шешу кезінде оқушыларда математикалық мәдениет, ой - өрісінің тереңдігі дамиды. Қорыта айтқанда, стандартты емес есептер оқушылардың интелектуалдық мүмкіндіктерін арттырады, ал стандартты есептер мұндай мүмкіндікті бермейді.

Стандартты емес есептер көбіне математикалық олимпиада есептері мен конкурстық есептерде кездеседі. Әдетте стандартты емес есептерді шешу үшін, стандартты емес әдістер қолданылатындығы түсінікті. Мұндай есептерді шешу үшін оқушыларда қосымша стандартты емес есептерді шешу әдістерінің қоры болуы керек.

Мектеп курсындағы алгебралық теңдеулерді тригонометриялық түрлендірулердің көмегімен шешу стандартты емес әдістердің бірі болып табылады. Тригонометриялық түрлендірулер өте күрделі және көпқадамды есептерді жеңіл шешуге мүмкіндік береді. Ол көбіне, негізгі әдістермен шешілмейтін немесе өте қиын шешілетін есептерді шешуде қолданылады.

Математиканың тереңдетіп оқыту сыныптарында, тригонометриялық турлендірулер көмегімен алгебралық есептерді шешуге қосалқы сағаттар беріледі, ал қарапайым сыныптарда мұндай сағаттар бөлінбейді. Сондықтан математикалық олимпиадаларда, көбіне математиканы тереңдетіп оқытатын сыныптардың оқушылары жоғарғы орындарды иеленіп жатады.

Зерттеу мақсаттары: Жоғарыда айтылғандарды ескере келіп, алгебралық теңдеулерді тригонометриялық түрлендірулердің көмегімен шешу әдістерін барлық мектеп сыныптарында енгізу қажеттілігі туындайды. Себебі:

1. Тереңдетіп оқыту курсты әртүрлі стандартты емес есептермен толықтыруға мүмкіндік береді. Ал ол өз кезегінде оқушылардың творчествалық мүмкіндіктерін дамытуға зор үлесін тигізеді. Сонымен қатар, тригонометриялық түрлендірулер күрделі олимпиада есептерін шешудің тиімді әдістерінің бірі болып табылады.

2. Математикалық мектептерге, немесе математиканың тереңдетіп оқыту мектептеріне және т. б. қабылдағанда оқушыларға күрделі есептер ұсынатындығы белгілі. Оқушыларға бұл есептерді шешу барысында стандартты емес әдістерді пайдалану қажеттілігі туындайды. Сондай әдістердің бірі тригонометриялық түрлендірулер болып табылады.

3. Тригонометриялық алмастырулар көмегімен шешілетін есептер жеткілікті түрде жоғарғы деңгейлі алгебралық мүмкіндіктер қандай қажеттілік тудырса, тригонометриялық алмастырулардың да соншалық мүмкіндігі бар. Бұл дегеніміз белігілі бір есепті шешуде қолайлы әдісті пайдаланып, оның шешу әдістерін бағалау болып табылады.

4. Оқушы тригонометриялық алмастыруларды қолдану барысында есепті шешу үшін алмастыру енгізу аргументтерін толықтай үйренеді.

Дипломдық жұмыс кіріспе, үш тарау, қорытынды, пайдаланған әдебиеттер тізімінен тұрады. «Стандартты емес теңдеулер мен теңсіздіктерді шешуді оқыту әдістемесі» атты тарауында негізгі түсініктер мен теңдеулерді шешу жолдары қарастырылған. «Алгебралық теңдеулерді шешуде тригонометриялық алмастыруларды қолдану» атты тарауында иррационал, рационал, көрсеткіштік және тағы басқа теңдеулерді тригонометриялық алмастыруларды қолданып шешу жолдары көрсетілген есептер қарастырылып, аталған тақырыптарға мысалдар келтірілген. «Алгебралық теңдеулерді шешуде компьютерлік технология көмегімен шешу» атты тарауында теңдеулерді заманауи талапқа сай арнайы математикалық пакеттердің көмегімен алгебралық теңдеулердің нақты шешімдері көрсетілген.

Пәні: Математиканы оқыту әдістемесі.

Зерттеу объектісі: Математикалық стандарты емес теңдеулер мен теңсіздіктер ұғымы.

Алгебралық есептерді шешу барысында тригонометриялық алмастыруларды қолдану бағытында математиканың әртүрлі бөлімдерімен өзара байланыс жасалған. Атап айтсақ, алгебра мен тригонометрия. Сонымен қатар есептерді шешу барысында туындайтын мәселелерді тез шешуге, есептерді шешуге қолайлы әдістерді іздеу арқылы белгілі нәтижеге қол жеткізу оқушыларды батылдылыққа, ізденімпаздыққа тәрбиелейді.

1 Стандартты емес теңдеулер мен теңсіздіктерді шешуді оқыту әдістемесі

1. 1 Теңдеулер мен теңсіздіктер жайлы ұғымның қысқаша тарихы

4000 жылдай бұрыңғы уақыттың өзінде-ақ вавилондықтар мен мысырлықтар жер өлшеу, құрылыс және әскери істерінің әр түрлі есептерін теңдеулер құрып шығарған. Бірінші және екінші дәрежелі теңдеулерді ежелгі заманда Қытай және Үнді ғалымдары да шеше білген.

Теңдеулер арқылы шығарылатын есептер ең ежелгі көптеген текстерде кездеседі. Мысалы, өсімдіктерден жасалған орам түріндегі Мәскеулік папируста б. э. дейінгі 1850 ж. шамасында жасалған жазуда және Ахмес папирусында кездесетін есептерде белгісіз шама ерекше символмен көрсетілген және “хау” немесе “аха” деп аталған. Ал бұл атау “мөлшер”, “үйме” деген мағынадағы сөз. “Үйме есептеуі”, немесе “хау есептеуі” деп аталған есептеу біздің, есепті теңдеулер арқылы шешуімізге азды-көпті сәйкес келеді.

Ахмес папирусындағы бір есеп және оны шешу мысалы мынадай:

1-есеп. “Мөлшер мен оның, төрттен бір бөлігін бірге алғанда 15 болады”.

Бұл есепті қазіргіше шығарғанда

х +1/4х=15 тендеуі құрылады.

Мұны шешкенде табатынымыз: х= 12.

Ахмес папирусында есеп шешуі былай басталады: “4-тен бастап сана; оның ширегін, яғни 1-ді алуға тиіссің; онымен бірге алғанда 5”. Мұнан кейін 15 саны 5-ке бөлінеді, бөлінді 4-ке көбейтіледі, сонда белгісіз 12 шығады.

Шешудің бұл мысырлық методы мәнісі жағынан болжау методы болып табылады. Шешуге кіріскенде белгісіз шама ретінде кез келген сан, бұл жерде 4 саны алынды, өйткені оның ширегі, 1, оп-оңай табылады. Онан кейін 4+1 = 5. Алайда есеп шарты бойынша нәтиже 5 емес, 15 болуға тиіс, демек, 15 саны 5-тен неше есе артық болса, белгісіз шама еркін алынған 4 санынан сонша есе артық болуға тиіс. [1]

Бұл метод орта ғасырларда Азия мен Европада кеңінен қолданылған және “жалған болжам методы” деп аталған. “Екі жалған болжам методы” да қолданылған болатын, ал бұл туралы сөз кейініректе болады.

Теңдеулер құруға берілген есептердің ең ежелгі алғашқыларына, сірә, ежелгі мысырлық Мәскеулік папирустағы кейбір есептерді жатқызуға болар. (Бұл папирус Мәскеудегі бейнелеу өнері музейінде сақтаулы. Оны зерттеген және жазуын анықтап таныған орыс ғалымдары. ) .

Мәскеулік папирустағы есептердің біреуі мынау.

2 - е с е п. “Сан және оның жартысы 9 болады” . Санды табу керек.

Бұл есепті шешуге арналған теңдеуді қазіргіше жазғанда мы-

нандай болады:

х+1/2х=9.

Ежелгі гректердің “геометриялық алгебрасында” теңдеулерді шешу мәселесі олардың оң шешімдері ретінде алынатын кесінділерді салу мәселесіне келіп саятын. Жаңа арифметикалық алгебраның бастамасы тек Диофантта кездеседі.

Грек математикасындағы біздіп, заманымыздың I-II ғасырларында басталған бетбұрыс, жана қаркын III ғасырдың ортасында өзінің шарықтау шегіне жетеді. Бұл самғау ежелгі дүниенін ең соңғы ұлы математигі Диофанттың математикалық шығармашылығынан көрінеді.

Диофант біздің заманымыздың 250 жылдары Александрияда өмір сүрген. Тек кана VI ғасырда грамматик Метродор антологиясында оның қанша жасағаны туралы бір жұмбақ есеп бар. Диофанттың кабірінің басына қойылған құлпытасқа осы жұмбақ есеп жазылса керек.

Диофанттың 13 кітаптан түратын, “Арифметика” деп аталатын көлемді еңбегінің бізге алтауы ғана жеткен. Бұл енбек түгелдей арифметика мен алгебра есептеріне арналған. Онда 180 есептің шығарылу жолы көрсетіледі. Арифметика Дионосий дейтін замандасына арнап жазылған. “Құрметті Дионосий, - деп бастайды еңбегін Диофант, - сенің сандар араласатын мәселелерді ерекше ынтамен оқып-зерттейтінінді ескеріп, мен олардың табиғаты мен құдіретін ең басынан бастап баяндап беруді мақұл көрдім”

Диофант “Арифметикасының” баяндау стилінің ежелгі грек математиктерінің канондарынан сапалы түрде екі өзгешелігі бар. Ол теңдеулердің шешуін геометриядан тыс таза арифметикалық-алгебралык әдістер арқылы жүргізеді.

Диофант теңдеулерінде белгісіз сан (аритмос) S сан коэффиценті болғанда белгісіздің таңбасынан кейін жазылады. Мысалы: s<a=11 аритомс-11x. Белгісіздің дәрежелерін Диофант сәйкес грек атауларының бас әріптерімен таңбалайды. x ² -“диафанис”S ^v x ³ -“кюбос” H ^v т. с. (алтыншы дәрежеге дейін ) . Диофантта белгісіздің кері шамасы да және оның дәрежелері де таңбаланады. Қосу, көбейту, бөлу таңбалары жоқ, азайту үшін ↑таңбасы алынған. Теңдік сөзбен немесе і әрпімен жазылады. Теңдеудің бос мүшесі үшін арнайын μ ⁰ таңбасы алынған, ол бірлік (монес) сөзінің бас әріпі. Сандар әріптер арқылы кескінделеді. Мысалдар келтірейік:

а) H ^v αsη↑δ ^v εμ ⁰ αιsα бізше x+8x-(5x ² +1) =теңдеуін белгілейді.

б) H ^v αδ ^v ιγδεεμ ⁰ βι бізше x ³ +13x ² +5x+2 көпмүшесін білдіреді.

Диофанттың “Арифметикасында” осындай символикамен белгіленген анықталған, анықталмаған теңдеулерге келтірілетін есептердің шешуі беріледі, ал ережелер мысалдар арқылы көрсетеді. Теңдеулердің оң бүтін және бөлшек шешулерін табуға аса назар аударылады. Шешуі теріс сан болатындай теңдеуді ол мағынасыз теңдеу деп санап, бүтіндей қарастырмайды. Диофонт иррацианал сандарды қолданбайды. Егер теңдеудің түбірі иррацианал болып келсе, есептің шартындағы берілгендерді іріктей отырып, жауабы рационал сандарға келетіндей етіп, есепті қайта құрады.

Анықталған теңдеуге арналған есептер сызықтық, квадрат, тек бір дербес жағдайда куб теңдеуге келеді. Диофант берілген теңдеуді канондық түрге келтіру үшін ұқсас мүшелерін топтау, теңдеудің екі жағына бірдей шамалар қосу арқылы теріс мүшені жою ережелерін көрсетеді. Ол тек бір оң, түбір табумен қанағаттанады. [9. 104]

а және Ь өзара жай сандар болып келген жағдайда ах+Ьу=1 түріндегі Диофант теңдеулерінің жалпы теориясын XVII ғасырдағы француз математигі Баше де Мезариа (1589-1638) құрады. Ол 1621 жылы Диофанттың “Арифметикасын” грек және латын тілдерінде түсініктемелер жазып бастырып шығарады. Екінші дәрежелі Диофант теңдеулерінің жалпы теориясын жасау жолында П. Ферма Дж. Валлис, Л. Эйлер, Ж. Лагранж, К. Гаусс сияқты көрнекті математиктер көп еңбек сіңірді. Осынын нәтижесінде, XIX ғасырдың басында екі белгісізі бар екінші дәрежелі рационал коэффициентті

ax ³ +bxy+cy ² +ax+by+f=0

теңдеуін жалпы түрде шешу проблемасы қарастырады. Диофант теңдеулері қазіргі математикада да жан-жақты зерттелуде.

Орта ғасырлар заманында алгебра, алгебралық символика бойынша жинақталған мағұлматтар, қол жеткен табыстар нәтижесіне XVI ғасырдың математиктері күн тәртібіне бұрыннан қойылған, көптен бері шешуі табылмай келе жатқан бірсыпыра ірі мәселелерді қолға алады. Солардың бірі- үшінші және төртінші дәрежелі теңдеулерді шешу үшін формулаларды қорытып шығару. Омар Хайям және басқа Шығыс оқымыстылары бұл проблеманы шеше алмай, болашаққа аманат ретінде қалдырып кеткенін жоғарыда айтқанбыз. Үшінші дәрежелі теңдеуге арналған осындай формуланы математика тарихында тұңғыш рет XVI ғасырда өмір сүрген Итальян математиктері Николо Тарталья (1500-1557) және Джироламо Кардалано (1501-1556) табады.

Үшінші және төртінші дәрежелі теңдеулерді радикалдар арқылы арқылы шешетін формуланы табу қайта өрлеу заманы математикасының үлкен жетістігі болды, міне осыдан бастап Европа математиктері ежелгі грек және орта ғасырдағы арай оқымыстылары жеткен деңгейге жетіп қана қоймай, олардан көш ілгері кетеді. Осыдан кейін енді математиктер бесінші және одан жоғары дәрежелі теңдеулерді шешудің жалпы формулаларын іздей бастады. Бұл сырт қарағанда шешілуі күмән туғызбайтын мәселе болғанымен, оның радиоканалдар арқылы формуланы табу оңай шаруа болмайды, осы бағытта көп ғасырлар 300 жыл бойы зерттеулер жүргізіп, XIX ғасырда n>4 болғанда алгабралық теңдеулерді жалпы түрде радикал арқылы шешуге болмайтының дәлелдейді. Мұны анықтағандар жас математиктер Галуа мен Абель болды.

Ал қазіргі заманда теңдеу мен теңсіздіктің классификациясы жасалып, стандартты емес түрлері ажыратылды. Осы тұста негізгі назарды Пойяның “Как решить задачу” (М. 1959. ) еңбегінде, Л. М. Фридманның “Теоретические основы методики обучения математике” (М. 1998), Сондай- ақ, осы ғалымның Е. Н. Турецкиймен бірігіп жазған “Как научиться решать задачи” (М. 1998. ) атты еңбектеріне аудару керек. Осында стандартты емес теңдеулер мен теңсіздіктерге, жалпы математикалық есептер жайлы түсінік беріп, оларды шешудің ең тиімді жолдарын көрсеткен. Сондай-ақ оқушылардың осы стандартты емес есептерден қиыншылықтарға ұшырайтындарының есебі анықталып, олардың алдын алу, стандартты емес есептерді шығара білуге үйретудің тиімді әдістеріне сәтті тоқталған.

1. 2 Стандартты емес есеп пен стандартты есеп арасындағы айырмашылықтары

Берілген есеп түріндегі есепті шешу алгоритмі бойынша мектеп курсындағы барлық есептер екі класқа жіктеледі: Стандартты немесе алгоритмдік есептер. Оларды шешу үшін мектеп курсында белгілі алгоритм болады. А. А. Ляпуновтың алгоритмге берген анықтамасын қабылдайық: “Берілген есепті шешу үшін алынатын алгоритм кез келген бастапқы мәндер, демек бастапқы ақпарат бойынша дұрыс жауапқа әкелетін жұмыс тәртібін қамтамассыз ететін элементарлы схема шегі тексерілген шарттардың бірігуі. ”

Стандартты емес есептер. Бұларды шешу үшін мектеп курсында нақты алгоритм жоқ. Стандартты емес есептерді шешу бір немесе бірнеше стандартты есепті шешуге әкеледі.

Неліктен мектеп оқушылары көп жағдайда есепті дұрыс шығарып, таныс емес есепті шешудің ең тиімді әрі жеңіл әдісін үйрене алмайды. Бұл мектепте есеп шығарудың дәстүрлі әдістемесімен байланысты (көбінесе солай аталса да, бұл әдістемені есеп шығаруды үйрету әдістемесі деп атау қиын) .

Мұғалімдердің жұмыс тәжірибесінің талдауы онда оқытудың бірнеше әдісін әр түрлі пропорцияда көрсетеді.

Алғашқы әдісте оқушылар шығару керек деп есептелетін барлық есептер көптеген типке бөлінеді. Бұл типтердің саны әртүрлі болуы мүмкін. Осылайша өткен ғасырда құралдар қатарына есептің жүзден артық типі ерекшеленетін, ал осы шақта олар азайса да, саны аз емес. Бұл есеп типологиясы есеп сюжетінің сызығымен де (сату мен сатып алу есептері, қозғалыс есептері, бірлескен жұмыс, қоспалар, т. б. есептер), мектепте оқытылатын математикалық алгоритм сызығымен де жүрді (алгебралық өрнектерді қалыпты түрге келтіру, қысқарған көбейту формулалары арқылы көпмүшені көбейткіштерге жіктеу, сызықтық теңдеу мен теңдеулер жүйесін шешу, рационалды теңсіздіктерді шешу, үшбұрыш жақтарын есептеу, көпбұрыштар, жазықтық пен қарапайым денелер көлемінің ауданын есептеп шығару, т. б. ) .

Есептің осындай әрбір типі үшін мұғалім бірнеше, мысал арқылы жете көрсететін, ғасырлар бойы қалыптасқан шығарудың типтік әдісі (алгоритм) бар. Содан соң, оқушылар бұл типтегі есептерді тақтада, үйде не сыныпта өз бетімен көп көлемде шығарады.

Бұл барлық есептер стандартты есептер класын құрады. Бұнда тек бір нәрсені ескеру керек.

Мәселе-мектепте оқытылатын есепті шығару алгоритмі оқу құралдарында, сондай - ақ мұғалімдер мазмұндамасында қысқартылған түрде беріледі. Математиканы жақсы меңгерген мұғалімге қысқарған алгоритмді ойша-ақ жіктеп ашу ешқандай қиындық келтірмейді. Бірақ оқушы (әсіресе әлсіз, керекті деңгейде оқытылмаған) қысқартылған алгоритмді қадамдар жіктелген бағдарламаға ойша ашу қиын.

Қысқартылған алгоритмдер математика курсында әртүрлі берілуі мүмкін: ауызша ережелер, формулалар, теоремалар және т. б. Осындай әрбір қысқартылған алгоритмді оқушыларды қадамдап жіктелген бағдарламаға, алдымен әрине әр қадамның тұжырымынан, содан соң осы әрекетті меңгергені бойынша ойша ашу керек.

Қысқартылған алгоритмдерді қадамдап жіктеу бағдарламасын қалай ашуға болатынын көрсететін мысал келтірейік:

1. Ауызша ереже. Осындай ереженің мысалы ретінде туынды дәрежесіне көтеру ережесі бола алады: туындының дәрежелерінің қосындысына тең.

Осы ереже негізінде осындай алынған алгоритмді құруға болады.

1 қадам - туындының барлық көбейткіштерін анықтау.

2 қадам - әр көбейткіштің берілген дәрежесін табу.

3 қадам - 2-ші қадам нәтижесін көбейту.

2. Формула. Мектепте төменде көрсетілген түрде берілетін квадрат теңдеу түбірінің формуласы осындай формуланың мысалы бола алады.

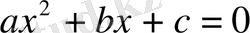теңдеуінің түбірлерін

(егер 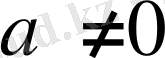және 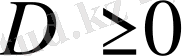, мұндағы )

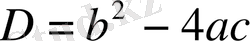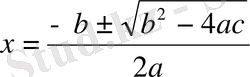формуласы арқылы табуға болады.

Бұл формуланы (қысқартылған алгоритм) осындай қадамдап жіктеу бағдарламасына ашу керек:

1 қадам - 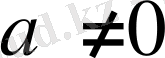шартын тексереміз. Егер ол орындалса, онда келесі қадамға көшеміз; егер де ол орындалмаса, онда берілген теңдеу квадрат емес және берілген формула қолданылмайды.

2 қадам -

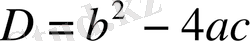
3 қадам - 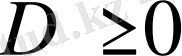шартын тексереміз. Егер ол орындалса, онда келесі қадамға көшеміз, егер ол орындалмаса, онда берілген теңдеу квадратты емес және берілген формула қолданылмайды.

4 қадам - түбір мәнін 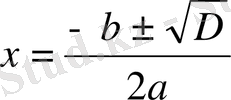формуласы арқылы табамыз.

2 және 4 - қадамдар күрделі және оларды қарапайым қадамдарға бөлуге болатынын байқаймыз.

3. Тепе-теңдік. Мысал ретінде 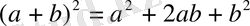теңдігін алайық.

1 қадам - екі мүшеліктің алғашқы мүшесін табу

2 қадам - екі мүшеліктің екінші мүшесін табу

3 қадам - екі мүшеліктің алғашқы мүшесін квадратқа шығару

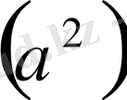
4 қадам - екі мүшеліктің екінші мүшесін квадратқа шығару

5 қадам - екі мүшеліктің бірінші, екінші мүшелерінің туындысын

табу

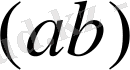
6 қадам - бесінші қадамның нәтижесін екіеселеу

7 қадам - үшінші, төртінші және алтыншы қадам нәтижелерін қосу.

Оқушыларға екімүшеліктің айырмасы үшін тепе-теңдік беру қажет емес екенін байқаңыз. Берілген тождество екімүшеліктің кез келген белгілері үшін қолданылады.

Мысал келтірейік:

4. Теорема. Көптеген теоремалар негізінде кез-келген өлшемдерді табу үшін ереже құруға болады.

Мысалы: осылайша Пифогор теоремасы бойынша егер катет ұзындығы немесе катет ұзындығын табу ережесі бар болса, егер гипотенуза ұзындығы немесе басқа катет ұзындығы берілген болса, гипотенуза ұзындығын табу ережесін құруға болады.

5. Анықтама. Кейде кейбір есептерді шешу ережесінің негізі ретінде сәйкес ұғымның ережесін алуға болады. Мысалы, бір айнымалысы бар теңсіздіктер жүйесінің шешімін анықтау негізінде: ”Бір айнымалысы бар теңсіздіктер жүйесінің шешімі деп - жүйенің әрбір теңсіздігіне қойғанда дұрыс болатын айнымаланың мәнін атайды”, - теңсіздіктер жүйесін шешудің осындай бағдарламасын құруға болады:

1 қадам - әрбір теңсіздік айнымалы үшін сандық аралықты оның шешімін алып, жүйенің әрбір теңсіздігін шешу;

2 қадам - алынған санды аралықтардың ортақ бөлігін табу.

1. 3 Жалпы стандартты емес есептерді шығару әдістемесі

Оқушылардың математикалық даму дәрежесі олардың есеп шығара білуінен анық байқалады. Есеп дегеніміздің өзі - әрбір мектеп оқушысының ақыл-ойын ұштаудың негізгі құралы. Әдеттен тыс, қызықты есептердің шешімін табу балалардың математикалық шығармашылығында маңызды орын алады. Ең әуелі, есеп шығаруды үйрену - оның шешімін табу екенін есте ұстаған жөн.

Кез келген қиын есепті шығару оқушыдан үлкен еңбекті, ерен күші мен табандылықты талап етеді. Бұл қасиеттер баланың есепке ынтасы оянғанда күшейе түседі. Қызықты есептер ақыл-ой энергиясын қозғалысқа келтіретіндіктен, оларды шешу оңайға түседі. Міне, сондықтан мүғалім оқушылар қызығып, өз еріктерімен шығаратын есептерді таңдап алуы қажет.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.