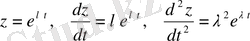Лаплас түрлендірулері арқылы сызықты дифференциалдық теңдеулерді шешу әдістері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:
М А З М Ұ Н Ы
КІРІСПЕ . . . 3
1. Сызықты дифференциалдық теңдеулер . . . 9
- Біртекті сызықты дифференциалдық теңдеулер . . . 9
1. 2 Біртекті емес дифференциалдық теңдеулердің жалпы
шешімінің құрылымы . . . 12
1. 3 Тұрақтыларды вариациялау әдісі . . . 13
1. 4 Тұрақты коэффициентті біртекті сызықтық дифференциалдық
теңдеудің фундаменталды шешімін Эйлер әдісімен құру . . . 16
1. 5 Тұрақты коэффициентті біртекті емес сызықтық дифференциал-
дық теңдеудің дербес шешімін құру . . . 20
2. Лаплас түрлендірулерінің сызықты дифференциалдық
теңдеулерді шешуде қолданылуы . . . 29
2. 1 Лаплас түрлендірулерінің негізгі түсініктері . . . 29
2. 2 Лаплас түрлендірулерінің қасиеттері . . . 31
2. 3 Лаплас түрлендіруін кері түрлендіру . . . 42
2. 4 Лаплас түрлендірулері арқылы дифференциалдық теңдеулерді
шешу . . . 51
ҚОРЫТЫНДЫ . . . 59
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 60
Кіріспе
Жаратылыстану ғылымындағы ең негізгі проблемалардың бірі-өзімізді қоршап тұрған табиғат құбылыстарындағы алуан түрлі процестерді зерттеу.
Қандай түрде болмасын құбылысты немесе процесті аяғына дейін білу үшін оның бүкіл ағымын басқаратын заңдылықты, былайша айтқанда өзгерісі қандай заңға бағынатынын зерттеу керек. Ал бұл заң - құбылыстың немесе процестің әрбір мезгілдегі күйінің өзгерісі және оны туғызушы бір себептің екіншісіне тәуелділігі өзімізді қоршап тұрған реалды дүниедегі алуан түрлі табиғаттық, қоғамдық процестерді ғылыми жолмен талдау, түптеп келгенде функциялық тәуелділікке келуден бұрын құбылыстың жалпы ағымын зерттеп, кез-келген уақыттағы оның күйін есептеп білу керек. Міне мұны шешу үшін кең түрде математикалық әдіс қолданылады.
Сызықты жәй дифференциалдық теңдеулер, дербес туындылы дифференциалдық теңдеулер, орама типті интегралдық теңдеулер, қолданбалы математиканың көптеген есептерін шешуде операциялық есептеулер қолданылады.
Операциялық есептеулер Лейбниц, Л. Эйлер, Лагранж, Лаплас, Фурье, Коши жұмыстарында қарастырылған. Ағылшын инженер-электригі Оливер Хевисайд операциялық есептеуді дифференциалдық теңдеулерді шешуде қолданып сымдағы электромагниттік толқындар теориясының күрделі мәселелері бойынша маңызды нәтижелер алған. Физикалық-техникалық есептерді шешу үшін қолданылатын символдық есептеулер қосымшаларын бірінші болып зерттеген О. Хевисайд болды. Сондықтан символдық есептеу- лерді О. Хевисайд атымен атады. Операциялық есептеулер зерттеуі Дж. Карсон, Бромвич, Леви және тағы басқа ғалымдар жұмыстарында интегралдық түрлендірулер негізінде мақұлданып зерттеу аясы кеңейе түсті.
Лаплас түрлендіруі
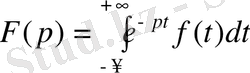 нақты айнымалы
нақты айнымалы
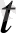 -нің түп-нұсқа функциялары
-нің түп-нұсқа функциялары
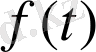 -нің кейбір кластарын комплекс айнымалы
-нің кейбір кластарын комплекс айнымалы
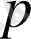 -нің бейне функциясы
-нің бейне функциясы
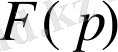 -ға түрлендіреді.
-ға түрлендіреді.
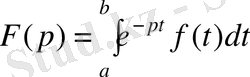 түрлендіруін алғашқы болып Л. Эйлер енгізді. Бұл түрлендірудің қасиеттерін Лаплас анықтап шексіз шектермен интегралдауды енгізді. Нәтижесінде Эйлер-Лаплас түрлендіруі басқа салаларда да қолданылатын болды. Америкалық инженер Дж. Карсон операциялық есептеу мен Лапластың интегралдық түрлендіруі арасындағы байланысты көрсетті және түпнұсқа
түрлендіруін алғашқы болып Л. Эйлер енгізді. Бұл түрлендірудің қасиеттерін Лаплас анықтап шексіз шектермен интегралдауды енгізді. Нәтижесінде Эйлер-Лаплас түрлендіруі басқа салаларда да қолданылатын болды. Америкалық инженер Дж. Карсон операциялық есептеу мен Лапластың интегралдық түрлендіруі арасындағы байланысты көрсетті және түпнұсқа
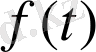 мен бейне
мен бейне
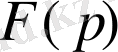 арасындағы қатынасты белгісіз
арасындағы қатынасты белгісіз
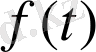 функциясына байланысты
функциясына байланысты
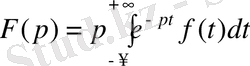 интегралдық теңдеу арқылы тағайындады. Ал түпнұсқа
интегралдық теңдеу арқылы тағайындады. Ал түпнұсқа
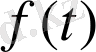 мен бейне
мен бейне
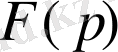 арасындағы кері тәуелділікті
арасындағы кері тәуелділікті
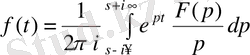
контурлы интеграл түрінде ағылшын математигі Томас Джон Бромвич алды.
Ол операциялық есептеулерді Лаплас түрлендіруі арқылы негіздеп математикалық көзқараспен қарағанда қатаң және нәтижелері Хевисайд жасаған операциялық есептеулердей әдіс жасады. Бірақ Хевисайдтың операциялық әдістеріне негіз алғаннан кейін тәжірибеде контурлы интеграл әдісінен гөрі Хевисайд әдісін бастапқы түрінде қолданылғаны тиімді деген қорытындыға келді.
Дипломдық жұмыстың мақсаты: Лаплас түрлендіруін пайдалана отырып дифференциалдық теңдеулер шешімін табу.
Дипломдық жұмыстың негізгі нәтижелері: Дипломдық жұмысымда жәй дифференциалдық теңдеулер шешімін Лаплас түрлендірулері арқылы табу жолдары қарастырылған.
Нақты айнымалы
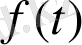 функциясының
Лаплас түрлендіруі
деп,
функциясының
Лаплас түрлендіруі
деп,
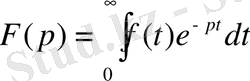 (1)
(1)
формуласымен анықталaтын комплекс айнымалы
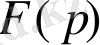 функциясын айтады.
функциясын айтады.
Теңдіктің оң жағындағы комплекс
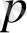 тәуелді меншіксіз интеграл
Лаплас интегралы
деп аталады.
тәуелді меншіксіз интеграл
Лаплас интегралы
деп аталады.
Үш шартты
1)
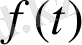 -функциясы
-функциясы
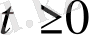 мәндерінде бөлшектеп - үздіксіз, яғни функция не үздіксіз немесе бірінші түрдегі санаулы үзіліс нүктелері бар.
мәндерінде бөлшектеп - үздіксіз, яғни функция не үздіксіз немесе бірінші түрдегі санаулы үзіліс нүктелері бар.
2)
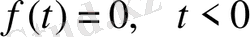 (2)
(2)
3)
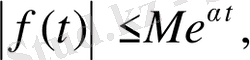
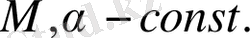 (3)
(3)
орындайтын кезкелген
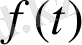 функциясын
түпнұсқа
(оригинал) деп атайды. (1) формуламен анықталатын
функциясын
түпнұсқа
(оригинал) деп атайды. (1) формуламен анықталатын
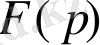 функциясы оның
бейнесі
(Лаплас бойынша бейнесі) деп аталады. Түпнұсқа
функциясы оның
бейнесі
(Лаплас бойынша бейнесі) деп аталады. Түпнұсқа
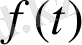 мен бейнесі
мен бейнесі
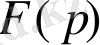 арасындағы сәйкестік мынадай түрде өрнектеледі:
арасындағы сәйкестік мынадай түрде өрнектеледі:
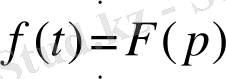 ,
,
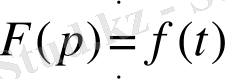
Теорема.
Функция
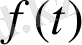 түпнұсқа делік. Онда Лаплас интегралы
түпнұсқа делік. Онда Лаплас интегралы
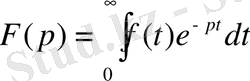
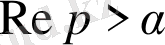 (яғни
(яғни
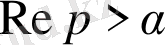 жарты жазықтығында),
жарты жазықтығында),
 3) шартындағы мәндерінде абсолютті жинақты және
3) шартындағы мәндерінде абсолютті жинақты және
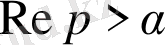 жарты жазықтығында аналитикалық функция болып, бейнені анықтайды.
жарты жазықтығында аналитикалық функция болып, бейнені анықтайды.
Лаплас түрлендірулерінің
негізгі қасиеттеріне
тоқталайын. Түпнұсқа функцияларды
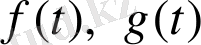 , . . . деп белгілеп, олардың Лаплас бойынша бейнелерін
, . . . деп белгілеп, олардың Лаплас бойынша бейнелерін
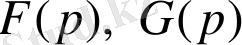 , . . . арқылы белгілейміз:
, . . . арқылы белгілейміз:
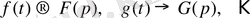 .
.
1. Сызықтық теоремасы.
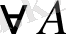 және
және
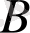 тұрақтыларында
тұрақтыларында
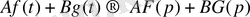 (4)
(4)
2. Ұқсастық теоремасы.
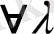 -тұрақтысында
-тұрақтысында
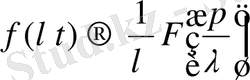 (5)
(5)
3. Өшу теоремасы
Кезкелген нақты немесе комплекс
 саны үшін
саны үшін
 .
.
4. Кешігу теоремасы.
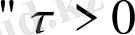 тұрақтысы үшін
тұрақтысы үшін
 . (6)
. (6)
5. Параметр бойынша дифференциалдау теоремасы.
Егер
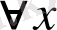 мәнінде
мәнінде
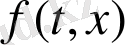 түпнұсқасына
түпнұсқасына
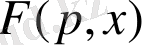 бейнесі сәйкестендірілсе, онда
бейнесі сәйкестендірілсе, онда
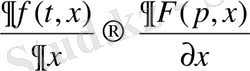 . (7)
. (7)
6. Түпнұсқаны дифференциалдау теоремасы
Егер
 болса, онда
болса, онда
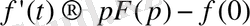 . (8)
. (8)
Дербес
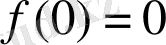 жағдайда
жағдайда
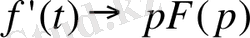 . (9)
. (9)
7. Түпнұсқаны интегралдау теоремасы.
Егер
 және
және
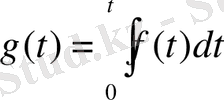 болса, онда
болса, онда
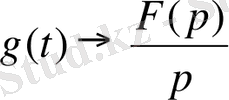 . (10)
. (10)
8. Бейнені дифференциалдау теоремасы.
Егер
 болса, онда
болса, онда
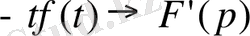 . (11)
. (11)
Бұл формула аналитикалық функцияны
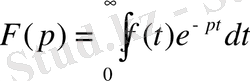 дифференциалдау ережесінен шығады
дифференциалдау ережесінен шығады
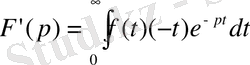 .
.
9. Бейнені интегралдау теоремасы.
Егер интеграл
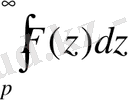 жинақы болса, онда
жинақы болса, онда
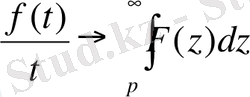 . (12)
. (12)
Анықтама.
Екі функцияның
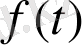 және
және
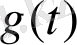 орамы деп
орамы деп
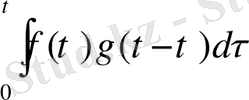
интегралын айтады.
Бұл интеграл
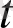 айнымалысының функциясы, айнымалы интеграл астындағы өрнекке де және жоғарғы шегі айнымалы етіп интеграл шегіне де енген. Функциялар орамын әдетте
айнымалысының функциясы, айнымалы интеграл астындағы өрнекке де және жоғарғы шегі айнымалы етіп интеграл шегіне де енген. Функциялар орамын әдетте
 түрінде белгілейді:
түрінде белгілейді:
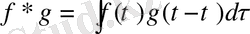 . (13)
. (13)
10. Бейнелерді көбейту теоремасы
Егер
 және
және
 болса, онда функциялар орамына
болса, онда функциялар орамына
 бейнелердің көбейтіндісі сәйкес
бейнелердің көбейтіндісі сәйкес
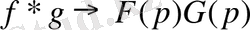 . (14)
. (14)
Көбейту теоремасы бойынша
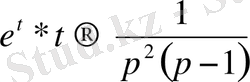 ,
,
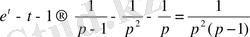 .
.
Осы сияқты
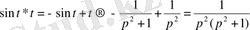 .
.
Қолданыста
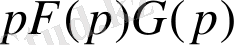 көбейтіндісі де кездеседі.
көбейтіндісі де кездеседі.
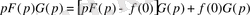 ,
,
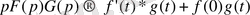 .
.
Орамды ашып жазсақ
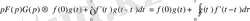 . (15)
. (15)
Формула (15) Дюамель интегралы деп аталады.
 ,
,
 және
және
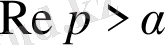 осы екі Лаплас интегралы да абсолютті жинақталатын жарты жазықтық делік.
осы екі Лаплас интегралы да абсолютті жинақталатын жарты жазықтық делік.
Екі бейненің орамы деп
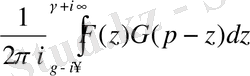 (16)
(16)
интегралын айтады, интегралдау сызығы
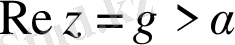 ,
,
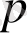 -комплекс айнымалы,
-комплекс айнымалы,
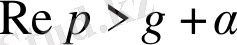 .
.
11. Түпнұсқаларды көбейту теоремасы
Егер
 және
және
 болса, онда
болса, онда
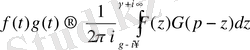 . (17)
. (17)
Кері түрлендіру теоремасы.
Егер
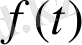 түпнұсқа,
түпнұсқа,
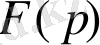 оның бейнесі болса, онда түпнұсқа
оның бейнесі болса, онда түпнұсқа
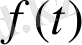 үзіліссіз болатын кезкелген
үзіліссіз болатын кезкелген
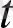 нүктесінде
нүктесінде
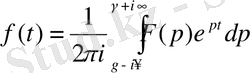 , (18)
, (18)
мұнда интегралдау
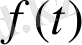 функциясының Лаплас интегралы абсолютті жинақты болатын жарты жазықтықтың кезкелген шексіз түзуі
функциясының Лаплас интегралы абсолютті жинақты болатын жарты жазықтықтың кезкелген шексіз түзуі
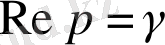 бойымен орындалады.
бойымен орындалады.
Жордан леммасы.
Функция
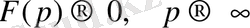 делік. Онда интеграл
делік. Онда интеграл
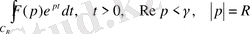
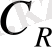 шеңбері бойымен
шеңбері бойымен
 нольге ұмтылады
нольге ұмтылады
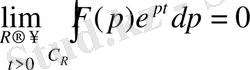 . (19)
. (19)
- Сызықты дифференциалдық теңдеулерБіртекті сызықты дифференциалдық теңдеулер
Екінші ретті дифференциалдық теңдеуді қарастырайық
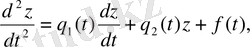 (1. 1)
(1. 1)
Дифференциалдық теңдеу шешімі деп (1. 1) дифференциалдық теңдеуін, қанағаттандыратын, үзіліссіз дифференциалданатын функцияны айтады.
Біртекті сызықтық теңдеудің үш негізгі қасиетіне тоқталайық.
. Егер
біртекті (1. 1) теңдеуінің шешімі болса, яғни
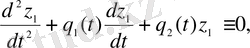
онда
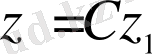 , (1. 2)
, (1. 2)
мұндағы С-кез-келген тұрақты, функциясы да осы теңдеудің шешімі болады.
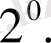 Егер
Егер
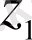 және
және
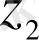 біртекті (1. 1) теңдеуінің шешімі болса, онда олардың қосындысы да
біртекті (1. 1) теңдеуінің шешімі болса, онда олардың қосындысы да
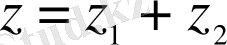 ,
,
(1. 1) теңдеуінің шешімі болады.
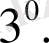 Егер
Егер
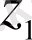 және
және
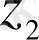 біртекті (1. 1) теңдеуінің шешімі болса, онда олардың сызықты комбинациясы да
біртекті (1. 1) теңдеуінің шешімі болса, онда олардың сызықты комбинациясы да
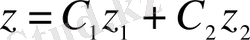 (1. 3)
(1. 3)
мұндағы
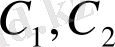 -кез-келген тұрақтылар, (1. 1) теңдеуінің шешімі болады.
-кез-келген тұрақтылар, (1. 1) теңдеуінің шешімі болады.
Анықтама.
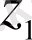 ,
,
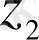 функциялары
функциялары
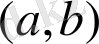 интервалында сызықты тәуелсіз деп аталады, егер олардың арасында мынадай қатынас орындалса:
интервалында сызықты тәуелсіз деп аталады, егер олардың арасында мынадай қатынас орындалса:
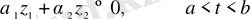 (1
.
4)
(1
.
4)
мұндағы
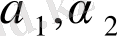 - барлығы бірдей нөлге тең емес тұрақты сандар.
- барлығы бірдей нөлге тең емес тұрақты сандар.
Қарсы жағдайда
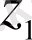 ,
,
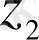 сызықты тәуелді деп аталады. (1. 4) шартын мынадай түрде түрлендіріп жазуға болады:
сызықты тәуелді деп аталады. (1. 4) шартын мынадай түрде түрлендіріп жазуға болады:
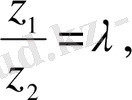 мұндағы
мұндағы
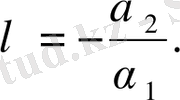
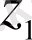 ,
,
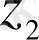 функцияларының бірінші ретті туындысы бар деп жорымалдап, анықтауыш құрамыз:
функцияларының бірінші ретті туындысы бар деп жорымалдап, анықтауыш құрамыз:
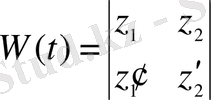
Бұл
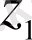 және
және
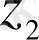 функциялары үшін Вронский анықтауышы немесе вронскиан деп аталады.
функциялары үшін Вронский анықтауышы немесе вронскиан деп аталады.
Сызықты тәуелділіктің қажетті және жеткілікті шарты келесі теоремада тұжырымдалады.
Теорема 1.
Егер
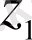 және
және
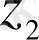 функциялары
функциялары
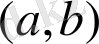 интервалында сызықты тәуелді болса, онда оның вронскиан
интервалында сызықты тәуелді болса, онда оның вронскиан
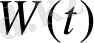 анықтауышы осы интервалда нөлге тепе-тең болады.
анықтауышы осы интервалда нөлге тепе-тең болады.
Теорема 2.
Егер коэффициенттері
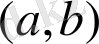 -да үзіліссіз
-да үзіліссіз
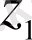 және
және
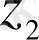 функциялары (1. 1) теңдеуінің сызықты тәуелсіз шешімдері болса, онда олардың Вронскиан
функциялары (1. 1) теңдеуінің сызықты тәуелсіз шешімдері болса, онда олардың Вронскиан
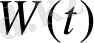 анықтауышы
анықтауышы
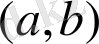 интервалының бірде-бір нүктесінде нөлге тең емес.
интервалының бірде-бір нүктесінде нөлге тең емес.
Тұжырымдардан мынадай қорытынды шығаруға болады: (1. 1) теңдеуінің екі шешімі сызықты тәуелсіз болуы үшін
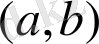 интервалының бірде-бір нүктесінде олардың вронскианы нөлге тең болмауы қажетті және жеткілікті.
интервалының бірде-бір нүктесінде олардың вронскианы нөлге тең болмауы қажетті және жеткілікті.
Шынында, егер
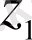 және
және
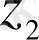 функциялары
функциялары
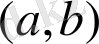 интервалында сызықты тәуелсіз болса, онда
интервалында сызықты тәуелсіз болса, онда
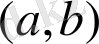 интервалында
интервалында
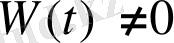 . Бірақ (1. 1) теңдеуінің екі шешімінің сызықты тәуелсіз екенін анықтау үшін вронскиан
. Бірақ (1. 1) теңдеуінің екі шешімінің сызықты тәуелсіз екенін анықтау үшін вронскиан
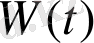 анықтауышының кемінде бір нүктеде нөлге тең емес екенін білу жеткілікті.
анықтауышының кемінде бір нүктеде нөлге тең емес екенін білу жеткілікті.
Анықтама. (1. 1) дифференциалдық теңдеуінің анықталған және сызықты тәуелсіз екі шешімі осы интервалда фундаменталды шешімдер жүйесі деп аталады.
Теорема 4
. Егер (1. 1) теңдеуінің коэффициенттері
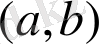 интервалында үзіліссіз болса, онда осы интервалда анықталған фундаменталды шешімдер жүйесі бар болады.
интервалында үзіліссіз болса, онда осы интервалда анықталған фундаменталды шешімдер жүйесі бар болады.
Дәлелдеуі.
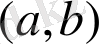 интервалынан
интервалынан
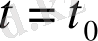 нүктесін алып бастапқы шарттары
нүктесін алып бастапқы шарттары
 (1. 5)
(1. 5)
болатын
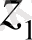 шешімін құрамыз. Сонан соң бастапқы шарттары
шешімін құрамыз. Сонан соң бастапқы шарттары
 (1. 6)
(1. 6)
болатын екінші шешім
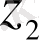 құрамыз. Құрылған шешімдердің
құрамыз. Құрылған шешімдердің
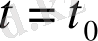 нүктесінде вронскианын есептейміз, сонда
нүктесінде вронскианын есептейміз, сонда
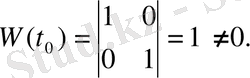
Ендеше
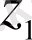 және
және
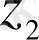 -әрбіреуі
-әрбіреуі
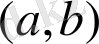 интервалында анықталған фундаменталды шешімдер жүйесі.
интервалында анықталған фундаменталды шешімдер жүйесі.
Теорема 4 дәлелденді.
(1. 5), (1. 6) теңдіктерінде 1 және 0 сандарының орнына анықтауышы нөлден өзгеше болатын кез-келген 4 санды алуымызға болады. Сонда
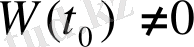
және тағы да фундаменталды шешімдер жүйесі алынады.
Анықтама.
Екінші ретті теңдеудің жалпы шешімі деп құрамында берілген теңдеудің барлық шешімі бар
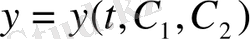 өрнекті айтады.
өрнекті айтады.
Негізгі теорема.
Егер
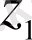 және
және
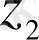 (1. 1) теңдеуінің фундаменталды шешімдер жүйесі болса, онда
(1. 1) теңдеуінің фундаменталды шешімдер жүйесі болса, онда
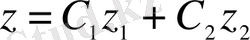 (1. 7)
(1. 7)
мұндағы
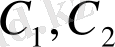 - кез келген тұрақтылар,
- кез келген тұрақтылар,
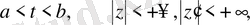 (1. 8)
(1. 8)
аймағында (1. 3) теңдеуінің жалпы шешімі болады.
Теорема 5. (1. 1) теңдеуінің екі сызықты тәуелсіз дербес шешімі бар болады.
Дәлелдеуі
. Дифференциалдық теңдеудің үш дербес шешімі бар болсын
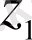 және
және
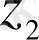 ,
,
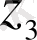 . Алғашқы екі шешімін қарастырайық. Егер олар сызықты тәуелді болса, онда үш шешімде сызықты тәуелді, өйткені мынадай қатынас орындалады:
. Алғашқы екі шешімін қарастырайық. Егер олар сызықты тәуелді болса, онда үш шешімде сызықты тәуелді, өйткені мынадай қатынас орындалады:
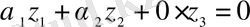
мұндағы
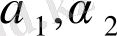 бірдей нөлге тең емес сандар. Егер
бірдей нөлге тең емес сандар. Егер
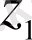 ,
,
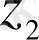 ,
,
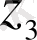 үш шешімі де сызықты тәуелсіз болса, онда негізгі теорема бойынша кез келген шешім, соның ішінде
үш шешімі де сызықты тәуелсіз болса, онда негізгі теорема бойынша кез келген шешім, соның ішінде
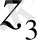 шешімі де
шешімі де
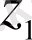 және
және
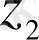 арқылы сызықты өрнектеледі:
арқылы сызықты өрнектеледі:
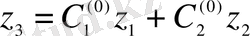 .
.
Олай болса
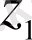 ,
,
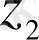 ,
,
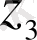 шешімдері қайтадан сызықты тәуелді.
шешімдері қайтадан сызықты тәуелді.
1. 2 Біртекті емес дифференциалдық теңдеулердің жалпы
шешімінің құрылымы
Біртекті емес дифференциалдық теңдеуді қарастырайық
(1. 9)
мұндағы
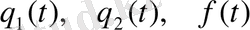 -
-
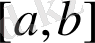 -да үзіліссіз.
-да үзіліссіз.
- теңдеуі үшіндербес шешімі табылған болсын. Ендеше
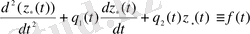 ,
(1. 10)
,
(1. 10)
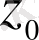 жаңа функцияны келесі формула бойынша енгіземіз
жаңа функцияны келесі формула бойынша енгіземіз
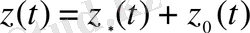 . (1. 11)
. (1. 11)
(1. 10) - дің оң жағын (1. 9) -ға қойсақ шығатыны:
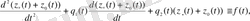
яғни
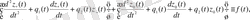
- теңдігі бойыншабіртекті теңдеуді қанағаттандыруы тиіс
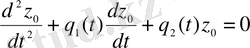 .
(1. 12)
.
(1. 12)
Алғашқы бөлімде көрсетілгендей егер
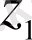 және
және
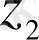 (1. 9) теңдеуінің фундаменталды шешімдер жүйесі, ал
(1. 9) теңдеуінің фундаменталды шешімдер жүйесі, ал
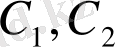 - кез келген тұрақтылар болса, онда оның жалпы шешімі
- кез келген тұрақтылар болса, онда оның жалпы шешімі
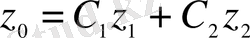 (1. 13)
(1. 13)
түрінде беріледі. (1. 13) теңдігінің оң жағын (1. 11) теңдеуіне қоямыз, сонда шығатыны:
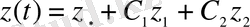 . (1. 14)
. (1. 14)
(1. 9) теңдеуінің барлық шешімі (1. 14) теңдеуінің құрамында бар. (1. 14) функциясы (1. 9) теңдеуінің берілген аймағындағы жалпы шешімі болып табылады. Сонымен, (1. 9) біртекті емес теңдеуінің жалпы шешімін табу үшін оның бір дербес шешімін тауып оған сәйкес біртекті (1. 12) теңдеуінің шешімін қоссақ жеткілікті.
Егер (1. 9) біртекті емес теңдеуінің оң жағы
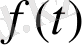 -функциясы екі қосындыдан тұратын болсын, яғни
-функциясы екі қосындыдан тұратын болсын, яғни
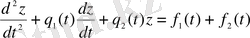 . (1. 15)
. (1. 15)
Бұл жағдайда берілген теңдеуді екі теңдеу түрінде қарстырамыз. Бірінші теңдеудің
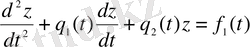
дербес шешімі
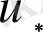 , ал екіншінің
, ал екіншінің
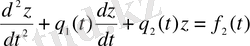
дербес шешімі
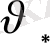 болса, онда
болса, онда
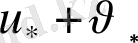 (1. 15) теңдеуінің дербес шешімі болады.
(1. 15) теңдеуінің дербес шешімі болады.
1. 3 Тұрақтыларды вариациялау әдісі
Екінші ретті біртекті емес дифференциалдық теңдеуді қарастырайық
(1. 16)
мұндағы
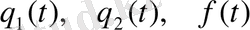 -
-
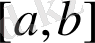 -да үзіліссіз.
-да үзіліссіз.
Бұл теңдеудің жалпы шешімін біртекті теңдеудің
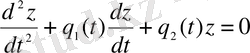 (1. 17)
(1. 17)
жалпы шешімі белгілі болғанда ғана анықтай аламыз.
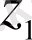 ,
,
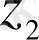 функциялары (1. 17) теңдеуінің фундаменталды шешімдер жүйесі болсын. Онда оның жалғыз шешімі
функциялары (1. 17) теңдеуінің фундаменталды шешімдер жүйесі болсын. Онда оның жалғыз шешімі
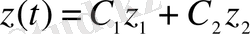 .
.
Тұрақтыларды вариациялау әдісін пайдаланамыз. Ол үшін
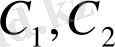 тұрақтыларын функция түрінде қолданамыз, яғни
тұрақтыларын функция түрінде қолданамыз, яғни
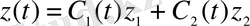 . (1. 18)
. (1. 18)
(1. 18) функциясы (1. 16) теңдеуінің шешімі болатындай етіп
 функцияларын таңдаймыз. Бұл функциялар (1. 18) функциясын (1. 16) теңдеуіне қойғанда пайда болатын тек бір ғана қатынасқа тәуелді. Сондықтан белгісіз
функцияларын таңдаймыз. Бұл функциялар (1. 18) функциясын (1. 16) теңдеуіне қойғанда пайда болатын тек бір ғана қатынасқа тәуелді. Сондықтан белгісіз
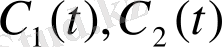 функцияларын анықтау үшін кез келген бір шартқа бағындыруға болады.
функцияларын анықтау үшін кез келген бір шартқа бағындыруға болады.
 тұрақтыларын анықтауда қарапайым теңдеулер жүйесін алу үшін (1. 18) функциясынан
тұрақтыларын анықтауда қарапайым теңдеулер жүйесін алу үшін (1. 18) функциясынан
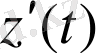 туындысын есептеп
туындысын есептеп
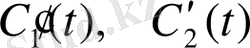 тұрақтылары бар өрнектерді нөлге теңестіреміз. Сонда мынадай теңдік аламыз
тұрақтылары бар өрнектерді нөлге теңестіреміз. Сонда мынадай теңдік аламыз
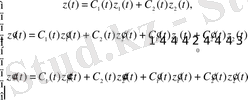
Табылған
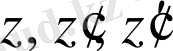 - мәндерді (1. 16) теңдеуіне қойсақ мынадай теңдік аламыз:
- мәндерді (1. 16) теңдеуіне қойсақ мынадай теңдік аламыз:


немесе
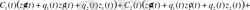
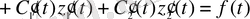 .
.
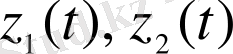 функциялары біртекті (1. 17) теңдеуінің шешімі болғандықтан
функциялары біртекті (1. 17) теңдеуінің шешімі болғандықтан
яғни
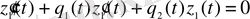 ,
,
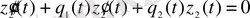 ,
,
соңғы теңдікті өзгертіп қайта жазайық
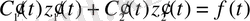 .
.
Сонымен
 белгісіздерін анықтау үшін келесі теңдеулер жүйесін алдық
белгісіздерін анықтау үшін келесі теңдеулер жүйесін алдық
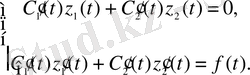 (1. 19)
(1. 19)
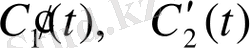 белгісіздеріне байланысты (1. 19) алгебралық теңдеулер жүйесі болғандықтан оның шешімі:
белгісіздеріне байланысты (1. 19) алгебралық теңдеулер жүйесі болғандықтан оның шешімі:
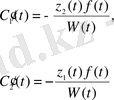 (1. 20)
(1. 20)
мұндағы
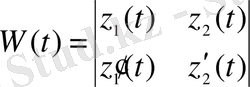 .
.
(1. 20) теңдігінің екі жағында интегралдаудан шығатыны:
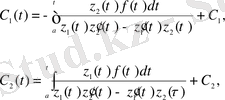
мұндағы
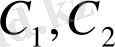 кез келген тұрақтылар.
кез келген тұрақтылар.
 функцияларының табылған мәндерін (1. 18) теңдеуіне қойсақ:
функцияларының табылған мәндерін (1. 18) теңдеуіне қойсақ:
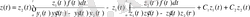
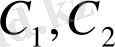 тұрақтылары нөлге тең болған жағдайда (1. 16) біртекті емес дифференциалдық теңдеуінің дербес шешімін аламыз
тұрақтылары нөлге тең болған жағдайда (1. 16) біртекті емес дифференциалдық теңдеуінің дербес шешімін аламыз
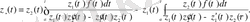 (1. 21)
(1. 21)
Дербес шешім (1. 21) бастапқы шарттарды қанағаттандырады, яғни
 .
.
Сонымен, (1. 16) біртекті емес дифференциалдық теңдеудің жалпы шешімін табу үшін (1. 17) біртекті теңдеудің фундаменталды шешімдер жүйесін құра білу жеткілікті. Сонан соң (1. 16) теңдеуінің жалпы шешімі квадратура арқылы табылады.
1. 4 Тұрақты коэффициентті біртекті сызықты дифференциалдық
теңдеудің фундаменталды шешімін Эйлер әдісімен құру
Біртекті емес дифференциалдық теңдеудің жалпы шешімін табу үшін оған сәйкес
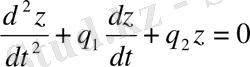 (1. 22)
(1. 22)
біртекті теңдеудің фундаменталды шешімдер жүйесін құру жеткілікті. (1. 22) дифференциалдық теңдеуінің фундаменталды шешімдер жүйесі элементар функциялардан құралады.
Бірінші ретті біртекті дифференциалдық теңдеудің
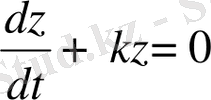 ,
,
Мұндағы
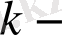 кез-келген тұрақты нақты сан
кез-келген тұрақты нақты сан
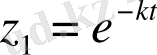
түрінде дербес шешімі бар. Эйлер бойынша (1. 22) екінші ретті біртекті сызықтық теңдеулер үшін дербес шешімді
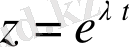 , (1. 23)
, (1. 23)
мұндағы
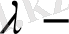 кез-келген уақытша анықталмаған тұрақты сан, түрінде іздестіреміз.
кез-келген уақытша анықталмаған тұрақты сан, түрінде іздестіреміз.
(1. 23) функциясының туындыларын
(1. 22) теңдеуіне қоямыз:
. (1. 24)
теңдікті
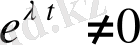 -не қысқартсақ мынадай теңдеу аламыз:
-не қысқартсақ мынадай теңдеу аламыз:
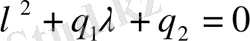 (1. 25)
(1. 25)
(1. 24) теңдігінен
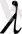 саны (1. 25) теңдеуінің шешімі болғанда ғана
саны (1. 25) теңдеуінің шешімі болғанда ғана
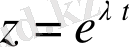 функциясы (1. 22) теңдеуінің шешімі екендігі анық. Бұл теңдеуді (1. 22) біртекті сызықты теңдеудің характеристикалық теңдеуі, ал оның түбірлерін характеристикалық саны деп атайды. Характеристикалық теңдеуді құру үшін (1. 22) теңдеуіндегі
функциясы (1. 22) теңдеуінің шешімі екендігі анық. Бұл теңдеуді (1. 22) біртекті сызықты теңдеудің характеристикалық теңдеуі, ал оның түбірлерін характеристикалық саны деп атайды. Характеристикалық теңдеуді құру үшін (1. 22) теңдеуіндегі
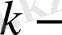 шы ретті туындыны
шы ретті туындыны
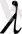 -ның
-ның
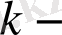 шы ретті дәрежесімен алмастыру жеткілікті.
шы ретті дәрежесімен алмастыру жеткілікті.
(1. 25) квадрат теңдеу болғандықтан оның екі шешімі болады. (1. 25) характеристикалық теңдеуді шешуде үш жағдай болуы мүмкін:
Жағдай 1.
(1. 25) теңдеуінің
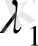 және
және
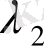 түбірлері нақты және әртүрлі:
түбірлері нақты және әртүрлі:
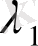 ,
,
 ,
,
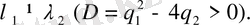 Бұл жағдайда (1. 25) теңдеуінің дербес шешімі
Бұл жағдайда (1. 25) теңдеуінің дербес шешімі
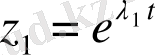 және
және
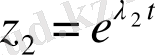 функциялары болады. Олар фундаменталды шешімдер жүйесін құрайды, өйткені олардың вронскианы
функциялары болады. Олар фундаменталды шешімдер жүйесін құрайды, өйткені олардың вронскианы
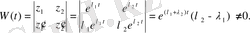
Демек, (1. 25) теңдеуінің жалпы шешімі формуласы бойынша мынадай болады:
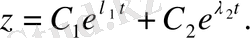 (1. 26)
(1. 26)
Жағдай 2.
(1. 25) теңдеуінің
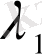 және
және
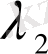 түбірлері нақты және бір-біріне тең:
түбірлері нақты және бір-біріне тең:
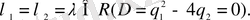
Бұл жағдайда тек жалғыз ғана дербес шешімі болады.
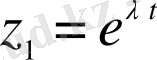 . Бірінші
. Бірінші
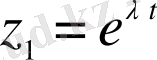 шешімімен бірге
шешімімен бірге
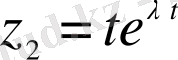 функциясы да (1. 22) теңдеуінің шешімі болатындығын көрсетеміз. Ол үшін
функциясы да (1. 22) теңдеуінің шешімі болатындығын көрсетеміз. Ол үшін
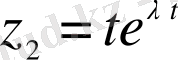 функциясын (1. 22) теңдеуіне қоямыз. Сонда:
функциясын (1. 22) теңдеуіне қоямыз. Сонда:
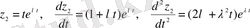
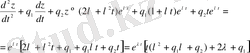
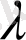 -саны (1. 25) теңдеуінің шешімі болғандықтан
-саны (1. 25) теңдеуінің шешімі болғандықтан
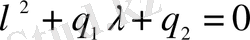
болады. Ендеше
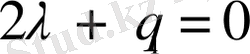 .
.
Шарт бойынша
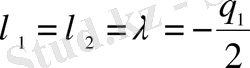 .
.
Сондықтан
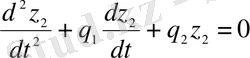 ,
,
яғни
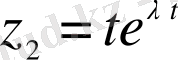
функциясы да (1. 25) теңдеуінің шешімі болады.
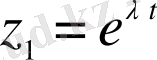 ,
,
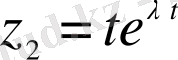
дербес шешімдері фундаменталды шешімдер жүйесін құрайды, өйткені
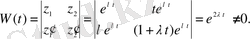
Сондықтан (1. 22) тұрақты коэффициентті сызықты біртекті дифференциалдық теңдеудің жалпы шешімі
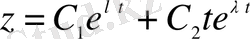 (1. 27)
(1. 27)
функциясы болады.
Жағдай 3.
(1. 25) теңдеуінің түбірлері
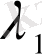 және
және
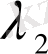 түйіндес - комлексті:
түйіндес - комлексті:
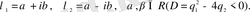
Ендеше шешім мынадай түрде болады:
 немесe
немесe
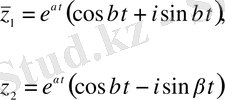 .
.
(1. 22) теңдеуінің екі дербес шешімін табамыз. Ол үшін екі сызықты комбинация құрамыз

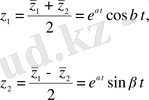 .
.
Екінші ретті біртекті сызықты дифференциалдық теңдеу шешімінің 3-ші қасиетінен
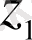 және
және
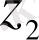 функциялары (1. 22) теңдеуінің шешімі болады. Бұл шешім фундаменталды шешімдер жүйесін құрайды, өйткені
функциялары (1. 22) теңдеуінің шешімі болады. Бұл шешім фундаменталды шешімдер жүйесін құрайды, өйткені
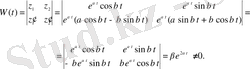
Сондықтан (1. 22) теңдеуінің жалпы шешімі мынадай түрде жазылады:
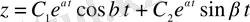
немесе
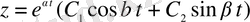 . (1. 28)
. (1. 28)
1. 5 Тұрақты коэффициентті біртекті емес сызықты дифференциал-
дық теңдеудің дербес шешімін құру
Екінші ретті сызықты біртекті емес тұрақты коэффициентті теңдеуді қарастырамыз
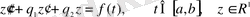 (1. 29)
(1. 29)
мұндағы
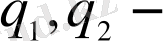 кез келген нақты сан,
кез келген нақты сан,
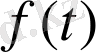 функциясы -
функциясы -
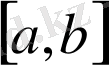 - да үзіліссіз. Егер сызықты біртекті теңдеудің фундаменталды шешімдер жүйесі табылса, онда (1. 29) теңдеуінің жалпы шешімін Лагранж әдісі бойынша анықтауға болады.
- да үзіліссіз. Егер сызықты біртекті теңдеудің фундаменталды шешімдер жүйесі табылса, онда (1. 29) теңдеуінің жалпы шешімін Лагранж әдісі бойынша анықтауға болады.
Егер
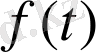 функциясы арнайы түрде болса
функциясы арнайы түрде болса
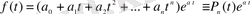
немесе
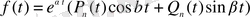
тұрақты коэффициентті (1. 29) теңдеуі үшін дербес шешімді табудың қарапайым жолы бар.
Бұл әдіс, яғни белгісіз коэффициенттер әдісінің негізгі мақсаты мынада: (1. 29) теңдеуіндегі
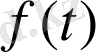 функциясының түріне қарап дербес шешім
функциясының түріне қарап дербес шешім
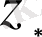 -ны белгісіз коэффициенттер арқылы жазып, (1. 29) теңдеуіне қояды да табылған тепе-теңдіктен белгісіз коэффициенттер мәндерін анықтайды.
-ны белгісіз коэффициенттер арқылы жазып, (1. 29) теңдеуіне қояды да табылған тепе-теңдіктен белгісіз коэффициенттер мәндерін анықтайды.
Жағдай 1. (1. 29) теңдеуінің оң жағы
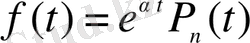
мұндағы
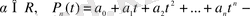
 ші дәрежелі көпмүшелік. Бұл жағдайда
ші дәрежелі көпмүшелік. Бұл жағдайда
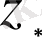 дербес шешімді келесі түрде іздестіреміз
дербес шешімді келесі түрде іздестіреміз
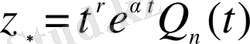 ,
,
мұндағы
 берілген теңдеуге байланысты құрылған
берілген теңдеуге байланысты құрылған
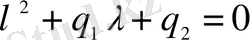
характеристикалық теңдеудің түбірі
 болғандағы еселігі, ал
болғандағы еселігі, ал
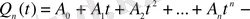
белгісіз коэффициенттер
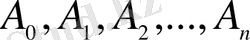 арқылы жазылған
арқылы жазылған
 ші дәрежелі көпмүшелік.
ші дәрежелі көпмүшелік.
а)
 саны
саны
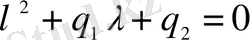 (1. 30)
(1. 30)
характеристикалық теңдеудің түбірі емес, яғни
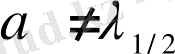 . Демек
. Демек

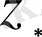 функциясын (1. 29) теңдеуіне қойғаннан кейін теңдеудің екі жағында
функциясын (1. 29) теңдеуіне қойғаннан кейін теңдеудің екі жағында
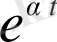 өрнегіне бөлеміз, сонда:
өрнегіне бөлеміз, сонда:

 яғни
яғни
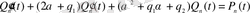 . (1. 31)
. (1. 31)
Соңғы теңдіктің сол жағында белгісіз коэффициенттермен жазылған
 ші дәрежелі көпмүшелік, ал оң жағында коэффициенттері белгілі
ші дәрежелі көпмүшелік, ал оң жағында коэффициенттері белгілі
 ші дәрежелі көпмүшелік.
ші дәрежелі көпмүшелік.
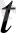 - нің бірдей дәрежесіндегі коэффициенттерін теңестіру арқылы
- нің бірдей дәрежесіндегі коэффициенттерін теңестіру арқылы
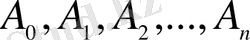 коэффициенттерін анықтау үшін
коэффициенттерін анықтау үшін
 алгебралық теңдеуден тұратын жүйе аламыз.
алгебралық теңдеуден тұратын жүйе аламыз.
Мысал 1.
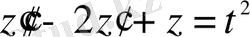 теңдеуінің жалпы шешімін табайық.
теңдеуінің жалпы шешімін табайық.
Шешімі. Берілген теңдеуге сәйкес біртекті теңдеудің
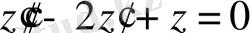
жалпы шешімін табамыз. Ол үшін оның характеристикалық теңдеуін құрамыз:
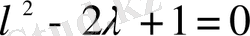 .
.
Бұл теңдеудің бір біріне тең екі түбірі
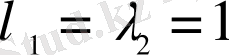 бар. Өйткені квадрат теңдеудің дискриминанты нөлге тең, яғни
бар. Өйткені квадрат теңдеудің дискриминанты нөлге тең, яғни
 . Ендеше біртекті теңдеудің жалпы шешімі
. Ендеше біртекті теңдеудің жалпы шешімі
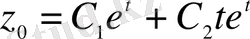
болады. Енді біртекті емес теңдеудің дербес шешімін іздестіреміз. Оның оң жағы
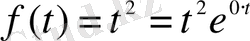 мына түрдегі
мына түрдегі
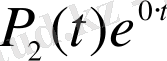 формулаға сәйкес келеді, мұндағы
формулаға сәйкес келеді, мұндағы
 характеристикалық теңдеудің түбірі емес. Сондықтан (2. 12) формуласы бойынша
характеристикалық теңдеудің түбірі емес. Сондықтан (2. 12) формуласы бойынша
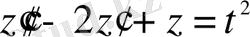
теңдеуінің дербес шешімін мына түрде іздестіреміз.
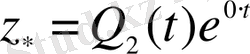 ,
,
яғни
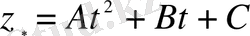 ,
,
мұндағы
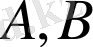 және
және
 - белгісіз коэффициенттер. Онда
- белгісіз коэффициенттер. Онда
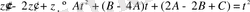 .
.
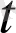 -нің бірдей дәрежедегі коэффициенттерін теңестіріп, белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін аламыз
-нің бірдей дәрежедегі коэффициенттерін теңестіріп, белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін аламыз
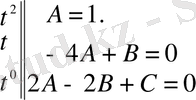
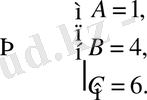 .
.
Сондықтан бастапқы теңдеудің дербес шешімі
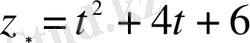 болады, ал біртекті емес теңдеудің жалпы шешімі
болады, ал біртекті емес теңдеудің жалпы шешімі
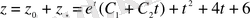 .
.
в)
 саны (1. 30) характеристикалық теңдеудің жәй түбірі болсын, яғни
саны (1. 30) характеристикалық теңдеудің жәй түбірі болсын, яғни
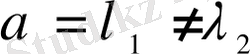 . Көпмүшеліктер тепе-теңдігін алу үшін
. Көпмүшеліктер тепе-теңдігін алу үшін
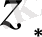 шешімінде
шешімінде
 -ші дәрежелі көпмүшелік алуымыз керек. Сондықтан
-ші дәрежелі көпмүшелік алуымыз керек. Сондықтан
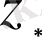 дербес шешімді
дербес шешімді

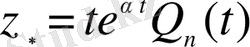 (1. 32)
(1. 32)
түрінде іздестіреміз.
Мысал 2.
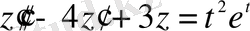
теңдеудің жалпы шешімін тап.
Шешімі.
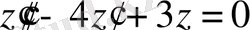
біртекті сызықты дифференциалдық теңдеу шешімін табамыз.
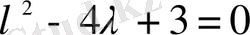
характеристикалық теңдеудің түбірлері
 . Демек, біртекті дифференциалдық теңдеудің жалпы шешімі
. Демек, біртекті дифференциалдық теңдеудің жалпы шешімі
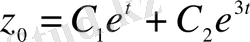 .
.
Енді біртекті емес теңдеудің дербес шешімін табамыз. Оның оң жағы
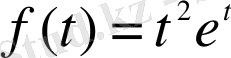
келесі формула
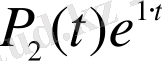 түріне келеді. Мұндағы
түріне келеді. Мұндағы
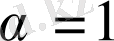 характеристикалық теңдеудің жәй түбірі. Сондықтан, (1. 32) формуласы бойынша теңдеудің дербес шешімі
характеристикалық теңдеудің жәй түбірі. Сондықтан, (1. 32) формуласы бойынша теңдеудің дербес шешімі
 ,
,
яғни
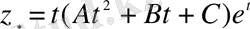 ,
,
мұндағы
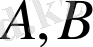 және
және
 - белгісіз коэффициенттер, түрінде іздестіріледі. Онда
- белгісіз коэффициенттер, түрінде іздестіріледі. Онда
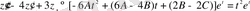 ,
,
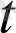 -нің бірдей дәрежедегі коэффициенттерін салыстыра отырып, белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін аламыз:
-нің бірдей дәрежедегі коэффициенттерін салыстыра отырып, белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін аламыз:
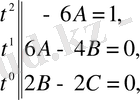
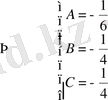
Сондықтан бастапқы теңдеудің дербес шешімі
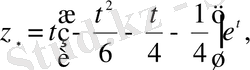 немесе
немесе
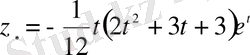 .
.
Ендеше тұрақты коэффициентті сызықты біртекті емес теңдеудің жалпы шешімі
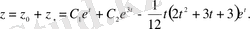
с)
 саны (1. 30) характеристикалық теңдеудің екі еселі түбірі болсын., яғни
саны (1. 30) характеристикалық теңдеудің екі еселі түбірі болсын., яғни
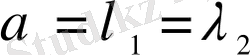 . Бұл жағдайда біртекті емес (1. 28) теңдеуінің дербес шешімін мынадай түрде іздестіреміз
. Бұл жағдайда біртекті емес (1. 28) теңдеуінің дербес шешімін мынадай түрде іздестіреміз

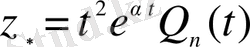 . (1. 33)
. (1. 33)
Мысал 3.
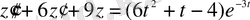 теңдеуінің жалпы шешімін тап.
теңдеуінің жалпы шешімін тап.
Шешімі.
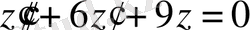 біртекті дифференциалдық теңдеудің шешімін табайық. Ол үшін характеристикалық теңдеу құрамыз
біртекті дифференциалдық теңдеудің шешімін табайық. Ол үшін характеристикалық теңдеу құрамыз
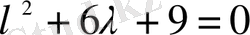 .
.
Бұл теңдеудің түбірлері
 . Демек, біртекті теңдеудің жалпы шешімі
. Демек, біртекті теңдеудің жалпы шешімі
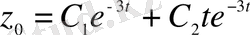
болады. Енді біртекті емес теңдеудің дербес шешімін қарастырайық. Берілген дифференциалдық теңдеудің оң жағы
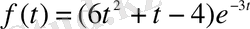
-
ке сәйкес келетін формула
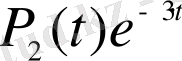 түрінде болады. Мұндағы
түрінде болады. Мұндағы
 характеристикалық теңдеудің екі еселі түбірі. Сондықтан, (1. 33) формуласына сәйкес теңдеудің дербес шешімін келесі түрде іздестіреміз
характеристикалық теңдеудің екі еселі түбірі. Сондықтан, (1. 33) формуласына сәйкес теңдеудің дербес шешімін келесі түрде іздестіреміз
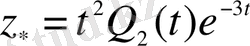 , яғни,
, яғни,
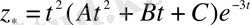 .
.
Мұндағы
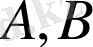 және
және
 -белгісіз коэффициенттер. Онда
-белгісіз коэффициенттер. Онда
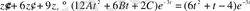 .
.
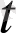 -нің бірдей дәрежесіндегі коэффициенттерді салыстырып белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін құрамыз:
-нің бірдей дәрежесіндегі коэффициенттерді салыстырып белгісіз коэффициенттерді анықтайтын теңдеулер жүйесін құрамыз:
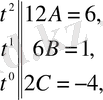
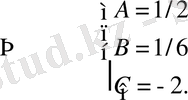
Сондықтан бастапқы теңдеудің дербес шешімі
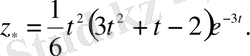
Ендеше тұрақты коэффициентті сызықты біртекті емес теңдеудің жалпы шешімі
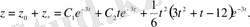
Жағдай 2. (1. 28) теңдеуінің оң жағы
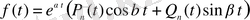 (1. 34)
(1. 34)
мұндағы
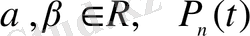 және
және
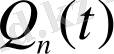 -кемінде біреуі
-кемінде біреуі
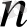 , жалпы дәрежесі
, жалпы дәрежесі
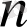 -нен аспайтын,
-нен аспайтын,
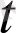 -дан тәуелді көпмүшелік. Олар тұрақты сан болуы немесе нөлге тепе-тең болуы да мүмкін. (1. 28) теңдеуі мынадай түрде жазылады:
-дан тәуелді көпмүшелік. Олар тұрақты сан болуы немесе нөлге тепе-тең болуы да мүмкін. (1. 28) теңдеуі мынадай түрде жазылады:
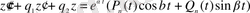 . (1. 35)
. (1. 35)
 және
және
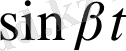 функцияларын Эйлер формуласы бойынша жазсақ
функцияларын Эйлер формуласы бойынша жазсақ
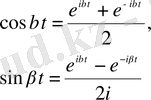
(1. 34) теңдеуі мынадай түрге келеді:
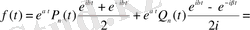
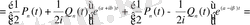 (1. 36)
(1. 36)
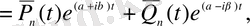
мұндағы
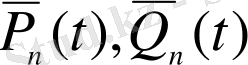
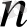 -ші дәрежелі көпмүшеліктер.
-ші дәрежелі көпмүшеліктер.
а)
егер
 және
және
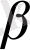 сандары
сандары
 (1. 30) характеристикалық теңдеудің түбірі болмайтындай сандар болса, онда (1. 35) теңдеуінің дербес шешімі мынадай түрде анықталады
(1. 30) характеристикалық теңдеудің түбірі болмайтындай сандар болса, онда (1. 35) теңдеуінің дербес шешімі мынадай түрде анықталады
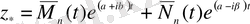
немесе нақты түрде
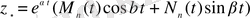 . (1. 37)
. (1. 37)
Мысал 4.
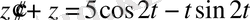 теңдеуінің жалпы шешімін тап.
теңдеуінің жалпы шешімін тап.
Шешімі.
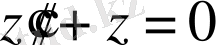 біртекті сызықты теңдеудің жалпы шешімін табамыз. Характеристикалық теңдеудің
біртекті сызықты теңдеудің жалпы шешімін табамыз. Характеристикалық теңдеудің
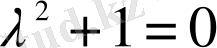
комплекс түдірлері бар, яғни
 . Демек, біртекті теңдеудің жалпы шешімі
. Демек, біртекті теңдеудің жалпы шешімі
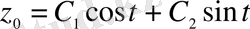 түрінде жазылады. Енді бастапқы теңдеудің дербес шешімін іздестіреміз. Берілген теңдеудің оң жағы
түрінде жазылады. Енді бастапқы теңдеудің дербес шешімін іздестіреміз. Берілген теңдеудің оң жағы
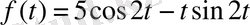
- ке сәйкес келетін формула
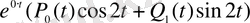 , мұндағы
, мұндағы
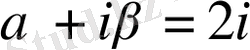
характеристикалық теңдеудің түбірі емес. Сондықтан (1. 37) формуласы бойынша берілген теңдеудің дербес шешімі
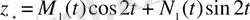 , яғни
, яғни
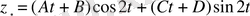
мұндағы
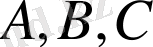 және
және
 - белгісіз коэффициерттер. Онда
- белгісіз коэффициерттер. Онда
 .
.
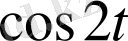 және
және
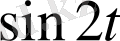 функцияларының коэффициенттерін салыстыру арқылы теңдеулер жүйесін құрамыз
функцияларының коэффициенттерін салыстыру арқылы теңдеулер жүйесін құрамыз

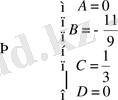
Сонымен
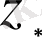 дербес шешімі мынадай:
дербес шешімі мынадай:
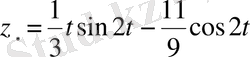 , ал бастапқы теңдеудің жалпы шешімі
, ал бастапқы теңдеудің жалпы шешімі
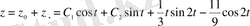 болады.
болады.
в)
егер
 және
және
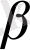 сандары
сандары
 (1. 30) характеристикалық теңдеудің түбірі болатындай сандар болса, онда (1. 35) теңдеуінің дербес шешімі мынадай түрде анықталады
(1. 30) характеристикалық теңдеудің түбірі болатындай сандар болса, онда (1. 35) теңдеуінің дербес шешімі мынадай түрде анықталады
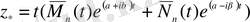
немесе нақты түрде
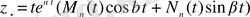 (1. 38)
(1. 38)
іздестіріледі.
Мысал 5.
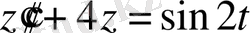 теңдеуінің жалпы шешімін тап.
теңдеуінің жалпы шешімін тап.
Шешімі.
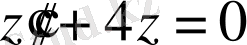 біртекті сызықты теңдеудің жалпы шешімін табамыз. Характеристикалық теңдеудің
біртекті сызықты теңдеудің жалпы шешімін табамыз. Характеристикалық теңдеудің
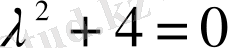 комплекс түдірлері бар, яғни
комплекс түдірлері бар, яғни
 . Демек, біртекті теңдеудің жалпы шешімі
. Демек, біртекті теңдеудің жалпы шешімі
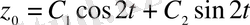
түрінде жазылады. Енді бастапқы теңдеудің дербес шешімін іздестіреміз. Берілген теңдеудің оң жағы
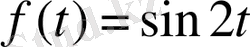 -
ке сәйкес келетін формула
-
ке сәйкес келетін формула
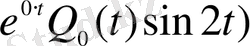 , мұндағы
, мұндағы
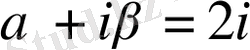
характеристикалық теңдеудің түбірі . Сондықтан (1. 38) формуласы бойынша берілген теңдеудің дербес шешімі

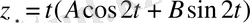
мұндағы
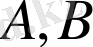 - белгісіз коэффициерттер. Онда
- белгісіз коэффициерттер. Онда
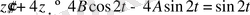 .
.
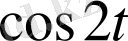 және
және
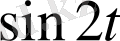 функцияларының коэффициенттерін салыстыру арқылы теңдеулер жүйесін құрамыз
функцияларының коэффициенттерін салыстыру арқылы теңдеулер жүйесін құрамыз
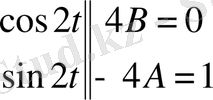
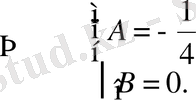
Сонымен
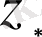 дербес шешімі мынадай:
дербес шешімі мынадай:
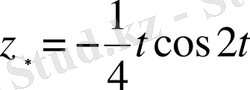 , ал бастапқы теңдеудің жалпы шешімі
, ал бастапқы теңдеудің жалпы шешімі
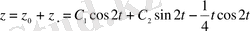
болады.
2 Лаплас түрлендірулерінің сызықтық дифференциалдық
теңдеулерді шешуде қолданылуы
2. 1 Лаплас түрлендірулерінің негізгі түсініктері.
Нақты айнымалы
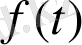 функциясының Лаплас түрлендіруі деп,
функциясының Лаплас түрлендіруі деп,
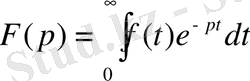 (2. 1)
(2. 1)
формуласымен анықталaтын комплекс айнымалы
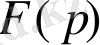 функциясын айтады.
функциясын айтады.
Теңдіктің оң жағындағы комплекс
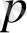 тәуелді меншіксіз интеграл Лаплас интегралы деп аталады.
тәуелді меншіксіз интеграл Лаплас интегралы деп аталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz