Жартылай жылу өткізбейтін қабатпен қапталған бірөлшемді стержендердегі жылу таралу мен термо-кернеулерді шекті элементтер әдісімен сандық модельдеу


Кіріспе
Өмірде күнделікті қолданылатын құрал саймандардың, техникалық жабдықтардың жасалу формасы, оның құрамы, физикалық өлшемдері және басқа да қасиеттеріне байланысты, оның қолдану ортасына бейімделіп, оған төзетіндей етіп жасап шығарылатынын біріміз білсек, біріміз білмейміз. Өйткені, табиғаттағы барлық денелердің физикалық қасиеттерін күрт өзгертіп жіберетін бір фактор бар, ол температура. Температура әсерінен физикалық денелер өзінің бастапқы күйінен айырылып қалпына келе алмай қалады. Осы факторды есепке ала отырып жасалып шығарылатын детальдің физикалық қасиеттерін өзгертіп жасап шығаруға болады. Яғни, сол ортаның температурасы белгілі болған жағдайда, физикалық дененің бойымен жылу таралу заңдылығын анықтап, ол жерге қойылатын детальдің қандай материалдан жасап шығарылуы керек екендігін анықтап беруге болады. Бұл өмірде көптеген инженерлік құрылымдарда кездесетін, нақты шекті шарттарда болатын бір өлшемді конструкциялық элементтердегі жылу таралу сияқты күрделі процеске шекті элементтер әдісін қолдану әдістемесін түсіндіру жолдары қарастырылған. Сонымен қатар күрделі құрылымды, кей жерінде жылу ағымдары, ішкі жабық қуыстар (көлбеу (горизонталь) орналасқан қуыстар) бар, жылу өткізбейтін және әртүрлі қоршаған ортамен жылу алмасатын бір өлшемді конструкциялық элементтердегі жылу таралу процессінің математикалық моделін құру әдістемесін, терең түрде талдап, зерттеулер жүргізуге мүмкіндік береді. Физикалық өлшемдерді және олардың интерпретациясын толық түрде көрсету, сол сияқты қарастырылатын мәселенің варияциялық қойылымына, шешілетін теңдеулер жүйесіне және есептеу алгоритіміне үлкен мән беріледі.
Нақты қолдану аясына байланысты конструкцияның әртүрлі элементтерінің стационарлы жылу таралуына күрделі есептердің шешімдері келтірілген. Сондай - ақ, өндірісте көптен - көп ішкі жабық қуыстары бар стержендер кездеседі. Нақты айтқанда, дизелмен жүретін жүк машиналарының клапондары іші қуыс етіп жасалады. Оның бірден - бір себебі, клапонның төңірегінде 2000 - нан жоғары температура болады. Сондықтан клапон балқып кетпес үшін, оның бойындағы температураны тез таратып жіберу мақсатында істетіледі. Яғни, ішінде қалған қуыстың жылу өткізгіштік қасиеті өте жоғары болады. Ішкі жабық қуыстары бар стержендер қолдану аясына байланысты өте күрделі болып келеді. Сондықтан сондай стерженнің бойымен жылу таралу процесін зерттеп анықтауда өте күрделі болады. Ол үшін құрылған математикалық моделді, күрделі интегралдарды шешу үшін компьютердің көмегіне жүгінеміз. Ең бастысы стерженді бөлшектеу (дискреттеу) арқылы стерженнің бойындағы жылу таралу процесін үлкен дәлдікпен анықтай аламыз.
Жұмыстың мақсаты . Жылу энергиясы мен потенциалдық энергияның минимумын табуда шекті элементтер әдісін қатар қолдана отырып жартылай жылу өткізбейтін қабатпен қапталған сырықтық элементтерге тұрақталған әртүрлі жылу көздері әсер еткенде, негізгі шешуші теңдеулер жүйесін құру және оны шешу арқылы жылжу, сығу, деформация және кернеулердің сырық ұзындығы бойынша таралу өрісін анықтап, термо - кернеулік есептерін сандық шешу және оларды талқылау.
Ғылыми жаңалығы . Жартылай жылу өткізбейтін қабатпен қапталған шекті ұзындықтағы жылу энергиясын өрнектейтін функционалды үш нүктелі квадраттық шекті элементтердің түйін нүктелеріндегі температуралар бойынша минимизациялап, зерттеліп жатқан сырық ұзындығы бойынша жылу өрісі заңдылығын табу.
Практикалық құндылығы . Жартылай жылу өткізбейтін қабатпен қапталған шекті ұзындықтағы сырықтардың әртүрлі жылу көздері мен созушы күштер әсерінде жұмыс жасағанда олардың ұзындықтары бойынша жылу таралу заңдылықтарымен қатар, жылжу, серпімділік деформация, кернеу, температуралық кернеу өрістерін табумен негізгі кернеу және сығушы күш мәндерін зерттеудің сандық алгоритміне сәйкес DELPHI объектілі бағдарлама кешенін жасаумен анықталды.
Жұмыстың көлемі мен құрылымы . Дипломдық жұмыс 62 компьютерлік бетті құрайтын кіріспе, 2 бөлім, негізгі нәтижелермен тұжырымдардан, қорытындыдан және пайдаланылған әдебиетер тізімінен тұрады.
Бұл диплом жұмысы физика, механика және қолданбалы математика саласында оқитын студенттермен қатар, өндірістің қолданбалы есептерін шешу үшін пайдалы болуы мүмкін.
Осылардың барлығы түсінікті болуы үшін көптеген математикалық және есептеуіш процедуралар DELPHI-6 объектіні бағдарлау бағдарламасында бағдарламалық кешені жасалды.
- ЖЫЛУ ҚҰБЫЛЫСТАРЫ. КОНСТРУКЦИЯЛЫҚ ЭЛЕМЕНТТЕР
ТҮСІНІГІ. ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІ
- Жылу өткізгіштік, конвекция
Энергияның басқа түрлері сияқты, ішкі энергия да бір денеден екінші денеге берілуі мүмкін. Жылу берілуінің мұндай түрін жылу өткізгіштік деп атайды. Жылу өткізгіштікті мына тәжірибеден байқауға болады. Жуан мыс сымның бір ұшын штативке қысып ұстатып қойып, оған балауызбен бірнеше ұсақ шеге жапсытырып қояды (1. 1. 1-сурет) .

1. 1. 1-сурет. Металдардың жылу өткізгіштігі
Сымның бос ұшын спирт шамның жалынына ұстап қыздырғанда, балауыз еріп, шегелер сымнан біртіндеп ажырап түсе бастайды. Сонда алдымен олардың сымның бос ұшына жақынырақ тұрғандары түседі, содан соң қалғандары кезегімен біртіндеп түсе береді.
Жылу сымның бойымен қалай беріледі?
Ыстық жалын әуелі сымның бір ұшындағы металл бөлшектерінің тербелмелі қозғалысын күшейтеді, сонда оның осы ұшының температурасы жоғарылайды. Сонан соң қозғалыстың осы күшеюі көрші бөлшектерге беріледі де, олардың тербелістерінің жылдамдығы артады, яғни сымның келесі бөлігінің температурасы жоғарылайды. Бұдан соң келесі бөлшектердің тербеліс жылдамдығы артады т. с. с. Мұндағы бір ескеретін нәрсе, жылу өткізгіштікте заттың өзі дененің бір ұшынан екінші ұшына қарай орын ауыстырмайды.
Әр түрлі заттардың жылу өткішгіштігі әртүрлі болады. Бұған әр түрлі металдардан жасалған стерженьдердің бойымен жылудың қалай берілетіндігіне тәжірибе жасап көз жеткізуге болады (1. 1. 2-сурет) .

1. 1. 2-сурет. Металдардың жылу өткізгіштік қасиетін салыстырмалы түрде көрсетілуі.
Бір заттардың екінші бір заттарға қарағанда жылуды жақсы өткізетіндігін біз өмір тәжірибесінен де білеміз. Мысалы, темір шегені құр қолмен ұстап тұрып, ұзақ уақыт қыздыруға болмайды, ал жанып тұрған шырпыны жалыны қолға тигенше, ұстап тұруға болады.
Жылуды металдар, әсіресе күміс пен мыс жақсы өткізеді. Балқыған металдардан, мысалы сынаптан, басқа сұйықтардың жылу өткізгіштігі шамалы ғана болады. Газдардың жылу өткізгіштігі одан да нашар болады. Өйткені олардың молекулалары бірінен - бірі алыс орналасады да, қозғалыстың бір молекуладан екіншісіне берілуі қиынға соғады.
Жүн, түбіт, аң терісі талшықтарының араларында ауа болады да сондықтан олар жылуды нашар өткізеді. Жануарларды суықтан олардың жүні, түбіті сақтайтындығы да осыған байланысты. Жануарларды суықтан ет пен тері арасындағы май қабаты да сақтайды, мұндай май суда жүзетін құстарда, киттерде, морждарда, ит балықтарда болады.
Жылуды ең нашар өткізетін - вакуум, яғни сиректелген газ. Мұны былай түсінуге болады: жылу өткізгіштік, яғни энергияның дененің бір бөлігінен екінші бөлігіне тасымалдануы, молекулалар немесе басқа бір бөлшектер арқылы іске асырылады, демек, бөлшектер жоқ жерде жылудың өткізілуі де болмақ емес.
Жылуды нашар өткізетін заттар жылуды сақтау қажет болатын жерлерде пайдаланылады. Мысалы, кірпіш қабырғалар үй ішіндегі жылуды сақтауға септігін тигізеді. Жылуды нашар өткізгіштердің жәрдемімен денені қызып кетуден де сақтауға болады. Мысалы, погребтегі (жер төледегі) мұз еріп кетпес үшін, погребті сабан, ағаш үгінділері, топырақ сияқты жылуды нашар өткізгіштермен жауып, қымтап қояды.
Конвекция.
Сұйықты және газды әдетте төменгі жағынан қыздырады. Суы бар шәйнекті отқа қояды, бөлме ішіндегі ауаны жылытатын батареяны терезе түбіне, еденге жақын орнатады. Бұл кездейсоқ жағдай ма?
Қолымызды ыстық плитаның немесе жанып тұрған лампаның үстіне ұстасақ, біз олардан жылы ауа ағыны жоғары көтерілетіндігін байқаймыз. Бұл ағын лампаның үстіне орналастырылған кішкене қағаз зырылдауықты шыр айналдыруы да мүмкін (1. 1. 3-сурет) .

1. 1. 3-сурет.
Бұл жерде біз жылу берілісінің конвекция деп аталатын басқа бір түрін бақылап отырмыз.
Конвекцияда жылу газдың немесе сұйықтың ағыны арқылы тасымалданады. Ыстық плитаға немесе лампаға тиіп тұрған ауа қызады да ұлғаяды. Ұлғайған ауаның тығыздығы суық ауаның тығыздығынан кем болады, сондықтан жылы ауа қабаты суық ауаның ішімен өрлей жоғары көтеріледі. Өйткені жылы ауаға суық ауа тарапынан жоғары қарай әсер ететін архимедтік күш жылы ауаға төмен қарай әсер ететін ауырлық күшінен артық болады. Сонан кейін суық ауаның келесі қабаты қызады да, жоғары қарай көтеріле бастайды т. с. с.
Сұйықты қыздырғанда да жылу дәл осылайша тасымалданылып беріледі. Қыздырғанда сұйық қабаттары орын ауыстырып араласатындығын байқау үшін ішінде суы бар шыны колбаның түбіне бір бояғыш заттың, мысалы марганец қышқыл калийдің ұсақ кристалын тастайды да, колбаны отқа қояды. Сонда су тұйық сызықтар бойымен орын ауыстыра бастайды - циркуляция жасайды, судың қызған астыңғы қабатын суық су ығыстырып жоғары шығарады (1. 1. 4-сурет) .
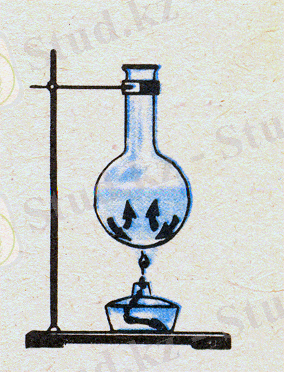
1. 1. 4-сурет.
Осы циркуляцияның нәтижесінде су тұтасымен біркелкі қызады. Мұнда да, газдағы сияқты, жылуды бір орыннан екінші орынға заттың - судың - ағыны тасымалдайды.
Конвекция құбылысы өзіміз тұратын бөлмелерде де болып жатады (1. 1. 5-сурет), соның арқасында үй ішіндегі ауа бір қалыпты жылынып тұрады.

1. 1. 5-сурет.
Біз табиғи немесе еркін конвекцияны қарастырдық. Егер біркелкі қызбаған сұйықты (немесе газды) насоспен немесе араластырғышпен араластырса, онда еріксіз конвекция болады.
Пробиркаға құйылған суды (1. 1. 6-сурет) көрсетілгендей етіп ысытып көрейік.

1. 1. 6-сурет.
Судың жоғарғы қабаты қайнайды да, төменгі қабаттары сол суық күйінде қала береді. Егер пробирка түбіне ұсақ мұз кесектері салынған болса, олар тіпті ерімейді де. Бұл неліктен? Суды осылайша қыздырғанда конвекция болмайды, өйткені судың қызған үстіңгі қабаты оның төменгі ауырырақ суық қабаттарының астына түсе алмайды. Мүмкін су жылу өткізгіштік арқылы қызатын болар? Бірақ тәжрибеге қарағанда судың жылу өткізгіштігі аз, сондықтан су түгел қызу үшін көп уақыт кеткен болар еді. Пробиркадағы ауаны үстіңгі жағынан қыздырғанда (1. 1. 7-сурет), оның неге түгел қызбайтындығын да дәл осылайша түсіндіруге болады.

1. 1. 7-сурет.
Молекулаларының қозғалысы шектеулі болатын қатты денелерде конвекция бола алмайды. Кристалл қатты заттардың әрбір бөлшегі айналасындағы басқа бөлшектермен өзара күшті тартылысып, бір ғана нүктенің төңірегінде тербеліп тұратындығын еске түсірейік. Сондықтан қатты денені қыздырғанда онда зат ағыны пайда бола алмайды. Күнделікті тәжірибе де осыны дәлелдейді. Қатты денелерде жылу тек жылу өткізгіштік арқылы ғана беріледі.
- Бірөлшемді конструкциялық элементтерге шекті элементтер әдісін қолданудың негізгі әдістемесі
Ең алдымен бірөлшемді конструкциялық элементтер дегеніміздің не екенін негіздейік. Бұлар көлденең қимасы тұрақты және айнымалы болатын биік телемұнаралар, фермалық көпірлер, қалың қабырғалы трубалар, арматуралар, рельстер элементтері және т. с. с. Ұзыннан ұзақ мұнай құбырлары мен темір жол арнасы да бірөлшемді конструкциялық элементтер болып табылады.
Енді шектелген L ұзындықты бірөлшемді конструкцияны қарастырайық
(1. 2. 1 а-г- сурет) .
1. 2. 1 а-г - сурет. Бірөлшемді конструкциялық элементтер түрлері.
Қолайлы болу үшін 1. 2. 1-в-суретіне тоқталайық. Осы стерженнің ұзындығымен, қандай да бір (1. 2. 2-сурет) заңдылықпен температураның мәні таралсын.
1. 2. 2-сурет. Бірөлшемді толық стерженнің ұзындығы бойынша температура мәнінің таралуы.
Берілген стерженді 4 түйіннің көмегімен ойша әртүрлі үш бөлікке бөлейік (1. 2. 3-сурет) .
1. 2. 3-сурет. Қарастырылып жатқан стерженнің дискреттелуі (бөлінуі) .
(Бұл жерде айта кету керек, берілген стерженді ұзындығы әртүрлі болатын қалағанымызша бөліктерге бөлуге болады) .
 Қарастырылып жатқан стерженнің әрбір бөлігі екі түйінмен шектелген. Мысалы нүктелерімен шектелген стерженнің бөлігі бірінші шекті элемент (ШЭ) болады, ал шектелген бөлігі екінші ШЭ болады да, соңғы нүктелермен шектелген бөлігі үшінші ШЭ болады. 1, 2, 3 және 4 нүктелері бірөлшемді сызықты шекті элементтер түйіндері деп аталады. Бұл элементтердің сызықтығы, температураның мәні әрбір шекті элемент аралығында сызықты таралады деген ұйғарымнан шығады. Әрине мұндай ұйғарым шындыққа жанасады, егер әрбір шекті элементтің ұзындығы жеткілікті аз болса.
Қарастырылып жатқан стерженнің әрбір бөлігі екі түйінмен шектелген. Мысалы нүктелерімен шектелген стерженнің бөлігі бірінші шекті элемент (ШЭ) болады, ал шектелген бөлігі екінші ШЭ болады да, соңғы нүктелермен шектелген бөлігі үшінші ШЭ болады. 1, 2, 3 және 4 нүктелері бірөлшемді сызықты шекті элементтер түйіндері деп аталады. Бұл элементтердің сызықтығы, температураның мәні әрбір шекті элемент аралығында сызықты таралады деген ұйғарымнан шығады. Әрине мұндай ұйғарым шындыққа жанасады, егер әрбір шекті элементтің ұзындығы жеткілікті аз болса.
Стерженнің 1, 2, 3, 4 нүктелеріндегі температураның мәнін сәйкесінше Т 1 , Т 2 , Т 3 және Т 4 арқылы белгілейік. Олар температураның түйіндік мәндері деп аталады. Олай болса шекті ұзындықты толық стерженнің ұзындығы бойынша температура мәні таралуының дискретті моделі 1. 2. 4-суреттегідей көрініс табады.
1. 2. 4-сурет. Толық стерженнің ұзындығы бойынша температураның таралу ауданының дискретті моделі.
Бұл сызықты дискретті моделде, әрине температураның мәні әрбір шекті элемент аралығында сызықты өзгереді. Яғни Т 1 және Т 2 , Т 2 және Т 3 , Т 3 және Т 4 -ті байланыстыратын сызықтар түзу болады (1. 2. 5-сурет) .
1. 2. 5-сурет. Әрбір шекті элемент аралығында температура мәнінің сызықты таралуының дискретті моделі.
Бұл жерде айта кету керек, әрбір шекті элемент аймағында температураның таралу аймағын квадратты, кубты және т. с. с. апроксимация жасауға болады. Бірақ та жылу өткізгіштіктің қолданбалы мәселелерін шешу үшін ШЭӘ қолдануды толық түрде түсіндіру жолында әрбір шекті элемент аймағында температура алаңын сызықты апроксимациялаумен шектелдік.
- Форманың сызықты функциясын құрудың әдістемесі
(Т, х) жүйесінде кез - келген бір i және j шектелген түйіндері бар ұзындығы l болатын шекті элементті қарастырайық (1. 3. 1-сурет) .
1. 3. 1-сурет. Дискретті шекті элемент.
Температураның (i) түйініндегі мәнін T i арқылы, (j) түйініндегі мәнін T j арқылы белгілейік. Форманың сызықты функциясы деп қандай да бір Т(х) функциясын атаймыз, егер ол, қарастырылып жатқан (i) және (j) түйіндерімен шектелген шекті элементтің аймағында, температура мәнінің таралуының сызықты заңы болып табылса.
(i) және (j) екі түйін арасында температураның мәні сызықты өзгереді деген ұйғарымымызға байланысты (x
i
 x
x
 x
j
) аралығында Т(х)
x
j
) аралығында Т(х)
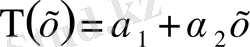 (1. 3. 1)
(1. 3. 1)
заңымен сипатталады. Бұл жерде
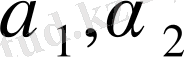 тұрақтылар.
тұрақтылар.
x=x
i
нүктесінде температураның мәні T(x
i
) =T
i
; ал x=x
j
нүктесінде T(x
j
) =T
j
деп ұйғарайық. Онда (1. 3. 1) бойынша
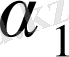 және
және
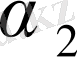 коэффициенттеріне байланысты екі теңдеуден тұратын теңдеулер жүйесін аламыз
коэффициенттеріне байланысты екі теңдеуден тұратын теңдеулер жүйесін аламыз
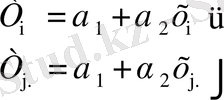 (1. 3. 2)
(1. 3. 2)
Бірінші теңдеуді екіншіден шегеріп келесі өрнекті аламыз
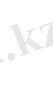
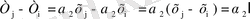
Бұл жерден шығатыны
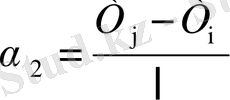 (1. 3. 3)
(1. 3. 3)
Енді табылған
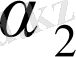 мәнін (1. 2. 2) теңдеулер жүйесінің бірінші теңдеуіне қоямыз
мәнін (1. 2. 2) теңдеулер жүйесінің бірінші теңдеуіне қоямыз
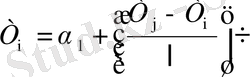 ,
,
бұл жерден
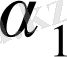 - ді анықтаймыз
- ді анықтаймыз
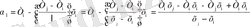
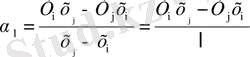 . 3 (1. 3. 4)
. 3 (1. 3. 4)
Табылған
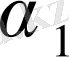 және
және
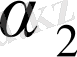 тұрақтыларының мәндерін (1. 3. 1) формуласына қойып, қарастырылып жатқан шектелген
тұрақтыларының мәндерін (1. 3. 1) формуласына қойып, қарастырылып жатқан шектелген
 ұзындықты элемент аймағында температура мәнінің таралу заңын анықтайтын өрнек аламыз.
ұзындықты элемент аймағында температура мәнінің таралу заңын анықтайтын өрнек аламыз.
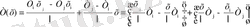
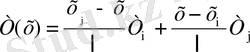 (1. 3. 5)
(1. 3. 5)
(1. 3. 5) өрнегінде T
i
және T
j
түйіндік мәндерінің алдындағы сызықты функцияларды қарастырайық, және сәйкесінше оларды
 және
және
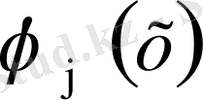 арқылы белгілейік.
арқылы белгілейік.
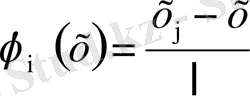
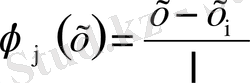 (1. 3. 6)
(1. 3. 6)
Бұл функциялар екі түйінді бірөлшемді шекті элемент үшін форманың функциясы деп аталады. Форма функциясының төменгі индекстері осы функцияның қай түйінге тиісті екенін көрсетеді. Бұл форма функциялары келесі қасиеттерге ие.
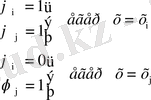 (1. 3. 7)
(1. 3. 7)
Сонымен қатар бұл форма функцияларының келесі қасиеттері бар
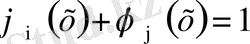
яғни,
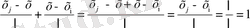
Бұл жерде айта кететін жайт, түйіндерді i және j арқылы нөмірлеу шартты түрде болды. Түйіндердің нөмірлері 1 мен 2, 5 пен 6, 20 мен 21 және т. с. с. болуы да мүмкін. Бірақ кез келген жағдайда (1. 3. 5) пен (1. 3. 6) өрнектері, сол сияқты (1. 3. 7) қасиеттері өз күшінде болады.
Бұл үшін келесі мысалды қарастырайық.
1-Мысал.
Толық стерженнің екі нүктесіндегі температураның мәні белгілі. Мысалға x і =6 координаталы нүктесінде температураның мәні Т 6 =218°С-қа тең, ал x j =10 координаталы нүктесінде T 10 =43°С.
Толық стерженнің 6
 x
x
 10 бөлігінде температураның мәні сызықты таралған деп алып, қарастырылып жатқан бөліктегі температура алаңының таралу заңын және температура градиентінің мәнін табу керек. Температураның мәнін x=7 см, x=8 см және x=8, 7 см координаталы нүктелерде табу керек.
10 бөлігінде температураның мәні сызықты таралған деп алып, қарастырылып жатқан бөліктегі температура алаңының таралу заңын және температура градиентінің мәнін табу керек. Температураның мәнін x=7 см, x=8 см және x=8, 7 см координаталы нүктелерде табу керек.
Шешуі. Қарастырылып жатқан есептің құрылымдық сызбасын құрайық (1. 3. 2-сурет) .
1. 3. 2-сурет. Есептің құрылымдық сызбасы
x
i
=6 см, x
j
=10 см, T
i
=218°С және T
j
=43°С деп алып (1. 3. 5) формуладан толық стерженнің 6
 x
x
 10 бөлігіндегі температураның таралу заңын табамыз.
10 бөлігіндегі температураның таралу заңын табамыз.
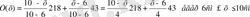
Т(х) өрнегін пайдаланып координата бойынша температура градиентінің мәнін табамыз
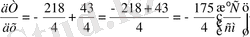
Бұл градиенттің физикалық мағынасы мынада, температураның мәні әр см ұзындықта
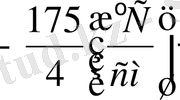 -ке азаяды. Мысалы x=6см нүктесінде температураның мәні 218°С тең, ал x =10 см нүктесінде, яғни келесі төртінші см ұзындықта оның мәні
-ке азаяды. Мысалы x=6см нүктесінде температураның мәні 218°С тең, ал x =10 см нүктесінде, яғни келесі төртінші см ұзындықта оның мәні
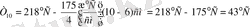 болады.
болады.
Сол сияқты градиенттің мәнін пайдаланып x=7 см, x=8 см и x=8, 7см координаталы нүктелерде де температураның мәнін табуға болады. Мысалы:
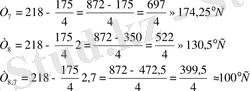
Бұл жерде, Т(х) толық стерженнің бөлігінде х-тің орнына сәйкесінше x=7 см, x=8 см және x=8, 7 см қойып, температура алаңының анықталған таралу заңын пайдаланып Т 7 , Т 8 және Т 8. 7 мәндерін табуға болады.
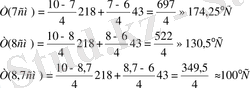
Осылайша, қарастырылап отырған шекті элемент аймағында температураның таралу заңы немесе температура градиентінің мәні арқылы (температураның түйінді мәндері белгілі болғанда) қарастырылып жатқан элементтің кез келген нүктесінде температураның мәнін есептеуге болады.
Енді осы мысалға форма функциясының қасиеттерін қарастырайық. Қарастырылып жатқан мысал үшін форма функциясының өрнегі келесідей болады.

Бұл жерде осы мысалда да форма функциясының қасиеттері сақталғанын көруге болады.
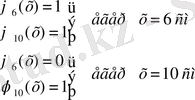
Форма функциясының басқа да қасиеттерін тексеруге болады.
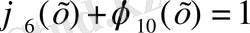
Шынымен де
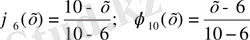 болады.
болады.
Олай болса
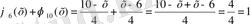
Осылайша форма функциясының қасиеттері барлық жерде бірдей болатынын анықтадық.
Екі түйінді бірөлшемді элементтер үшін форма функцияларын құруды толық меңгеру үшін, сонымен қатар осы функциялардың қасиеттерін апробациялау үшін келесі мысалды қарастырайық.
2-Мысал.
Екі түйінді бірөлшемді шекті элемент үшін форма функциясын құру қажет. Түйіндердің координаталары келесі: x 1 =7 см, x 2 =11, 6 см.
Берілген шекті элементке форма функциясын құру үшін (1. 3. 6) формуласын пайдалану қажет. Бұл жерде x i =х 1 =7 см, x j =x 2 =11. 6 см деп алу керек. Онда қарастырылып жатқан мысал үшін форма функциясының соңғы өрнегі келесі түрде болады:
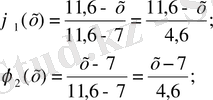
Енді форма функциясының қасиеттерін зерттейік
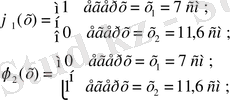
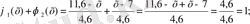
Екі түйінді бір өлшемді шекті элементтер үшін форма функцияларын құру әдістемесі қуыс трубалық стержендер, көлденең қимасы айнымалы болатын стержендер болған кезде де дәл осындай болады. Бірақ интегралдау процедурасын жасау кезінде бұл детальдар міндетті түрде ескеріледі.
2 СЫРЫҚТЫҢ ӘР ТҮРЛІ ЖЫЛУ КӨЗДЕРІ ӘСЕРІНЕН КЕРНЕУЛІК ДЕФОРМАЦИЯЛЫҚ КҮЙІН ЗЕРТТЕУ
2. 1 Жартылай жылу өткізбейтін қабатпен қапталған екі шеті қатаң бекітілген сырықта жылу табудың сандық алгоритмі
Бізге шекті ұзындықты
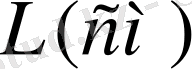 , көлденең қима ауданы ұзындығы бойынша тұрақты
, көлденең қима ауданы ұзындығы бойынша тұрақты
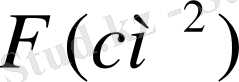 , бүйір беті жартылай жылу өткізбейтін қабатпен қапталған сырық беріліп, оның екі шеті қатаң бекітілсін (2. 1. 1-сурет) .
, бүйір беті жартылай жылу өткізбейтін қабатпен қапталған сырық беріліп, оның екі шеті қатаң бекітілсін (2. 1. 1-сурет) .
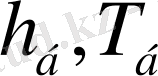
2. 1. 1-сурет. Әр түрлі жылу көздерінің әсеріндегі
екі шеті қатаң бекітілген сырық
Мұндай әр түрлі жылу көздерінің әсерінен сырықтың ұзындығы бойынша белгілі бір заңдылықпен жылу өрісі таралады. Ол заңдылықта шекті элементтер әдісі және жылу энергиясының функционалын түйін нүктелердегі температура мәндері бойынша минимизациялау әдісі арқылы табуға болады. Берілген сырықты үш нүктелі квадраттық шекті элементтермен бөлеміз және әрбір элемент үшін жылу энергиясын өрнектейтін арнайы функционалды жазамыз.
1) Шекті элементтің бүйір беті жылу өткізбейтін қабатпен қапталған, ал оның сол жақ шетіндегі көлденең қима ауданы арқылы
 жылу ағыны беріліп, оң жақ шетіндегі
жылу ағыны беріліп, оң жақ шетіндегі
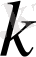 -нүктесі ішкі нүкте болсын (2. 1. 2-сурет) .
-нүктесі ішкі нүкте болсын (2. 1. 2-сурет) .
2. 1. 2-сурет. Сол жақ шетіндегі көлденең қима ауданы арқылы
 жылу ағыны берілген шекті элемент
жылу ағыны берілген шекті элемент
Мұндай элемент шегіндегі температураның таралуын үш нүктеден өткен екінші дәрежелі қисық сызық деп қарасақ, онда
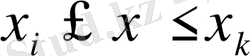 аралығында
аралығында
(2. 1. 1)
болып, мұнда
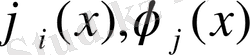 және
және
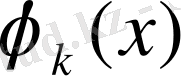 функциялары үш нүктелі квадраттық шекті элементтің пішін функциялары және олар (1. 1. 8) формулалар арқылы өрнектеледі.
функциялары үш нүктелі квадраттық шекті элементтің пішін функциялары және олар (1. 1. 8) формулалар арқылы өрнектеледі.
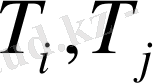 және
және
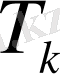 -лар элементтің
-лар элементтің
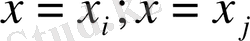 және
және
 нүктелеріне сәйкес температураның мәндері. Осы элемент шегіндегі температураның градиенті мынадай болады
нүктелеріне сәйкес температураның мәндері. Осы элемент шегіндегі температураның градиенті мынадай болады
, (2. 1. 2)
мұнда
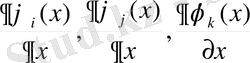 -туындылар (1. 1. 12) формуласы арқылы өрнектеледі. Онда жоғарыда сызылған элемент үшін жылу энергиясын өрнектейтін функционалдың көрінісі мынадай болады
-туындылар (1. 1. 12) формуласы арқылы өрнектеледі. Онда жоғарыда сызылған элемент үшін жылу энергиясын өрнектейтін функционалдың көрінісі мынадай болады
... жалғасы
, (2. 1. 3)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz