Цилиндрлік функциялар: Бессель, Ханкель және модификацияланған түрлерінің теориясы, қасиеттері және қолданылуы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 46 бет
Таңдаулыға:
М А З М Ұ Н Ы
КІРІСПЕ . . . 3
Арнайы функциялар теориясының жалпы теңдеулері . . . 4
Цилиндрлік функциялар түрлері . . . 6
0. 1 Бессель функциялары . . . 6
0. 2 Ханкель функциясы . . . 8
0. 3 Модифицирленген Бессель функциялары . . . 13
0. 4 Бурже функциялары . . . 14
0. 5 Біртекті емес Бессель функцияларының дербес шешімдері . . . 15
0. 6 Параболалық цилиндрлік функциялар . . . 17
0. 7 Кельвин функциялары . . . 19
1 Бессель теңдеулері
1. 1 Бессель теңдеулері . . . 22
1. 2 Бессель теңдеуінің шешімдері. Бірінші текті Бессель функциясы . . . 23
1. 3 Бессель теңдеуінің жалпы шешімі . . . 31
1. 4 Екінші текті Бессель функциясы . . . 33
1. 5 Бессель теңдеуіне келтірілетін теңдеулер . . . 37
1. 6 Бессель функциялары үшін рекурентті қатынас . . . 40
1. 7 Үшінші текті Бессель функциясы . . . 44
2 Модифицирленген Бессель функциялары
2. 1 Модифицирленген Бессель функциялары . . . 46
2. 2 Бессельдік функциялар жүйесінің туындылаушы (өңдеуші) функциясы.
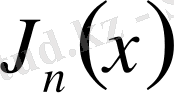 интегралдық көрсетілуі . . . 48
интегралдық көрсетілуі . . . 48
2. 2. 1 Натурал индексті Бессель функциялары бойынша жіктелуі . . . 48
2. 2. 2 Бессель функциясының интегралдық бейнелеуі . . . 51
3 Цилиндрлік функцияның асимптотикалық көрінісі
3. 1 Цилиндрлік функцияның асимптотикалық көрінісі . . . 55
3. 2 Цилиндрлік функциялардың нольдерінің үлестірілуі. Цилиндрлік функциялардың графиктері . . . 57
3. 3 Цилиндрлік функциялар жүйесінің ортогональдығы. Бессельдік функциялар бойынша қатарға жіктелуі . . . 61
ҚОРЫТЫНДЫ . . . 66
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 67
КІРІСПЕ
Дипломдық жұмыста цилиндрлік функциялар және олардың қолданылулары қарастырылған. Яғни цилиндрлік функциялардың түрлеріне тоқталып өткен және Бессель теңдеуінің шешімдері болатын Бессель функцияларының, модифицирленген Бессель функциялары және цилиндрлік функцияларның асимптотикалық көрінісі мен олардың қасиеттері берілген.
Диплом жұмысы кіріспеден, үш тараудан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады. Жұмыстың бірінші тарауында Бессель теңдеуінің анықтамасы және Бессель функциясының қасиеттері келтірілген. Ал екінші тарауында Бессель теңдеуінің шешімі туралы, І-текті, ІІ-текті, ІІІ-текті Бессель функциялары және модифицирленген Бессель функциясы туралы айтылған. Үшінші тарауда цилиндрлік функциялардың нольдерінің орналасуы туралы, интегралдық көрінісі туралы, ортогональдық жүйесі туралы және Бессель функциясының қатарға жіктелуі туралы, сонымен қатар цилиндрлік функциялардың асимптотикалық көрінісі туралы айтылған.
Диплом жұмысының мақсаты: Арнайы функциялар - цилиндрлік функциялардың түрлерін және олардың қолданылуын баяндау.
Арнайы функциялар теориясының жалпы теңдеулері
Тұрақты коэффициентті математикалық физика (жалпы түрде дербес туындылы) теңдеулерінің есептерін шешуде қолданатын айнымалылары бойынша жіктеп шешу тәсілін қолданғанда міндетті түрде Штурм-Лиувиль есебіне келеміз. Ол есеп бойынша: біртекті
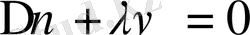 теңдеудің
теңдеудің
 аймақ шекарасы
аймақ шекарасы
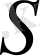 -те
-те
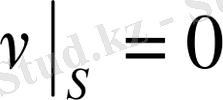 шекаралық шартын қанағаттандыратын сондай
шекаралық шартын қанағаттандыратын сондай
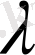 (меншікті) санға сәйкес нөлдік емес,
(меншікті) санға сәйкес нөлдік емес,
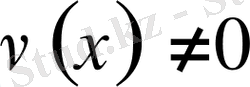 шешімін (меншікті функцияны) табу керек.
шешімін (меншікті функцияны) табу керек.
Егер
 аймақ
аймақ
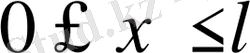 - кесінді;
- кесінді;
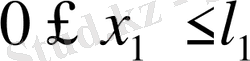 ,
,
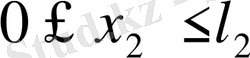 -төртбұрыш; параллепипед болса, онда
-төртбұрыш; параллепипед болса, онда
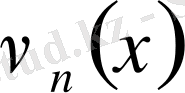 - меншікті функциялар тригонометриялық функциялармен өрнектелетін болады. Ал
- меншікті функциялар тригонометриялық функциялармен өрнектелетін болады. Ал
 аймақ шеңбер, цилиндр немесе шар түрінде болса, онда Штурм-Лиувиль түріндегі есептің меншікті функцияларын табу үшін цилиндрлік және сфералақ функциялар деп аталатын жаңа арнайы функциялар енгізіледі.
аймақ шеңбер, цилиндр немесе шар түрінде болса, онда Штурм-Лиувиль түріндегі есептің меншікті функцияларын табу үшін цилиндрлік және сфералақ функциялар деп аталатын жаңа арнайы функциялар енгізіледі.
Әдетте, физика теңдеулеріне қойылған есептерді айнымалыға жіктеп шешу тәсілі - жуықтап шешу тәсілі болғандықтан, жуық шешімнің жинақтылығын дәлелдеу үшін арнайы функцияларды талдап зерттеу мәселесі өте өзекті.
Қарапайым арнайы функциялар
Қарапайым арнайы функциялар
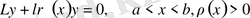 (0. 1)
(0. 1)
теңдеуінің шешімі болып келеді, мұндағы
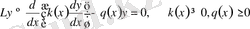
Дәлірек айтқанда, оның ішіндегі ең қарапайымы
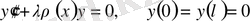
шеттік есептің, яғни (1) теңдеудегі
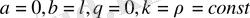 үшін меншікті функциялары тригонометриялық функцияларға сәйкес келеді.
үшін меншікті функциялары тригонометриялық функцияларға сәйкес келеді.
Енді, басқа арнайы функциялар үшін төмендегі теңдеулерді қарастырайық:
Бессель теңдеуі.
Бұл (1) теңдеудің
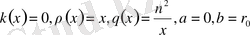 мәндеріне сәйкес келетін теңдеу:
мәндеріне сәйкес келетін теңдеу:
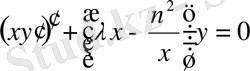
Лежандр теңдеуі
. Бұл (1) теңдеудің
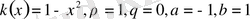 мәндеріне сәйкес келетін теңдеу:
мәндеріне сәйкес келетін теңдеу:
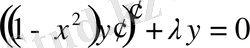
Лежандрдың жалғасушы функциясының теңдеуі.
Бұл (0. 1) теңдеудің
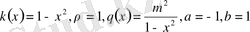 мәндеріне сәйкес келетін теңдеу:
мәндеріне сәйкес келетін теңдеу:
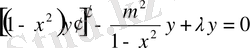
Чебышев-Эрмит теңдеуі.
Бұл (0. 1) теңдеудің
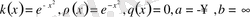 мәндеріне сәйкес келетін
мәндеріне сәйкес келетін
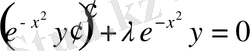
немесе
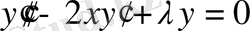
теңдеулер.
Чебышев-Лагерра теңдеуі.
Бұл (0. 1) теңдеудің
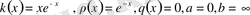 мәндеріне сәйкес келетін
мәндеріне сәйкес келетін
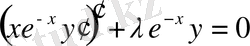
немесе
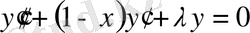
теңдеулер.
Бұл теңдеулердегі көңіл бөліп, арнайы қарайтын жағдайлар - теңдеулердегі
 коэффициенттің
коэффициенттің
 интервалының ең болмағанда бір шеткі нүктесіндегі нөлге айналуы. Себебі, осы
интервалының ең болмағанда бір шеткі нүктесіндегі нөлге айналуы. Себебі, осы
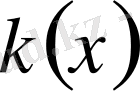 функцияның бұл қасиеті жоғарыдағы (1) теңдеулер үшін шекаралық есептердің қойылымында ерекше роль ойнайды. Бұл төменде осы
функцияның бұл қасиеті жоғарыдағы (1) теңдеулер үшін шекаралық есептердің қойылымында ерекше роль ойнайды. Бұл төменде осы
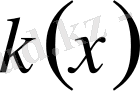 функцияның нөлге айналатын ерекше нүкте төңірегіндегі (0. 1) теңдеудің шешімінің қалай өзгеретінінің кейбір жағдайларын қарастырамыз.
функцияның нөлге айналатын ерекше нүкте төңірегіндегі (0. 1) теңдеудің шешімінің қалай өзгеретінінің кейбір жағдайларын қарастырамыз.
Цилиндрлік функциялар түрлері
Цилиндрлік функциялар - математикалық физика теңдеулері үшін айнымалыны алмастыру әдісін қолданып алынған қарапайым дифференциалдық теңдеулердің шешімі болатын бір айнымалылы арнайы функциялардың жалпы атауы болып табылады. Мысалы, цилиндрлік координаталардағы Лаплас теңдеулері, Пуассон теңдеулері, Гельмгольц теңдеуі және тағы басқалар. Негізінен айнымалы ретінде осьтерге дейінгі қашықтық алынады. Цилиндрлік функциялардың гармониялық функциялармен көбейтіндісі цилиндрлік гармонияны береді.
Жиі кездесетін цилиндрлік функциялар:
- Бессель функциялары
А) бірінші текті, шектелген;
Б) екінші текті («Нейман функциялары» деп те аталады), нольде шектелмеген;
2. Ганкель функциялары, бірінші және екінші текті - Бессель және Нейман функцияларының комплексті сызықты комбинациялары;
3. Модифицирленген Бессель функциялары - шектелмеген, монотонды, комплекс аргументтен тәуелді Бессель функциялары:
А) бірінші текті («Инфельд функциялары» деп те аталады) ;
Б) екінші текті («Макдональд функциялары» деп те аталады) ;
4. Бурже функциялары - Бессель функцияларының жалпыланған интегралдық бейнеленуі;
5. Біртекті емес Бессель функциялары дербес шешімдері:
А) Ангер функциялары;
Б) Вебер функциялары;
В) Струве функциялары;
Г) Ломмель функциялары;
6. Параболалық цилиндрлік функциялар;
7. Кельвин функциялары.
0. 1 Бессель функциялары
Анықтама . Бессель теңдеуі деп коэффициенттері айнымалы болатын, мынадай екінші ретті сызықты дифференциал теңдеуді айтамыз:
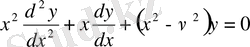 (0. 2)
(0. 2)
немесе
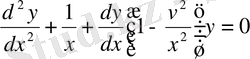 .
.
(0. 2) теңдеу сызықты болғандықтан, онда оның жалпы шешімі мына түрде жазылады:
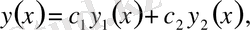
Мұндағы
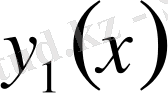 және
және
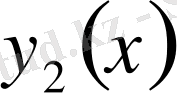 - екі тәуелсіз дербес шешімдер, ал
- екі тәуелсіз дербес шешімдер, ал
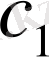 және
және
 - тұрақты шама.
- тұрақты шама.
(0. 2) теңдеудің шешімі Бессель функциясы немесе цилиндрлік функциялар деп аталатын арнайы функцияларды береді.
Теңдеуге енетін
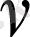 саны тұрақты шама болады. Ол (0. 2) теңдеудің
индексі
деп аталады, сонымен бірге
сәйкес цилиндрлік функцияның
реті
немесе
индексі
деп аталады.
саны тұрақты шама болады. Ол (0. 2) теңдеудің
индексі
деп аталады, сонымен бірге
сәйкес цилиндрлік функцияның
реті
немесе
индексі
деп аталады.
А) Бірінші текті Бессель функциялары
Анықтама: Мына қатармен анықталған функция,
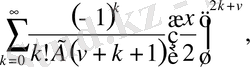
яғни
x
-тің кез келген мәнінде жинақталатын,
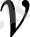 индексті бірінші текті
Бессель функциясы
деп аталады.
индексті бірінші текті
Бессель функциясы
деп аталады.
Бұл функцияны
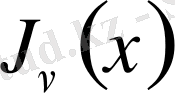 арқылы белгілеу қабылданған, яғни
арқылы белгілеу қабылданған, яғни
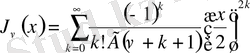 (0. 3)
(0. 3)
Б) Екінші текті Бессель функциялары
Бессель теңдеуінің бұл шешімі анықталмаған өрнек болады. Лопиталь ережесін пайдаланып, оның
 болғандағы шегін табамыз:
болғандағы шегін табамыз:
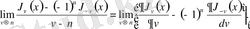
Бұл шекті
 болғандағы (0. 2) теңдеудің екінші шешімі ретінде қарастыруға болады.
болғандағы (0. 2) теңдеудің екінші шешімі ретінде қарастыруға болады.
Мұндай дербес шешім ретінде, мысалы, келесіні алуға болады:
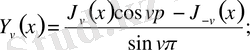 (0. 4)
(0. 4)
Бұл
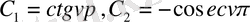 болғандағы Бессель теңдеуінің жалпы шешімінен алынады.
болғандағы Бессель теңдеуінің жалпы шешімінен алынады.
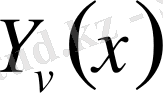 шешімі
бүтін емес индексті екінші текті Бессель функциясы
немесе
Нейман функциясы
деп аталады.
шешімі
бүтін емес индексті екінші текті Бессель функциясы
немесе
Нейман функциясы
деп аталады.
0. 2 Ханкель функциясы
Ханкель функциясы (үшінші текті Бессель функциялары) - бұл бірінші және екінші текті Бессель функцияларының сызықтық комбинациясы, ал олай болса, Бессель теңдеуінің шешімі болып табылады. Оны неміс математигі Герман Ханкельдің құрметіне қойған.
Индексі 0 болатын Ханкель функциялары Гельмгольц теңдеуінің фундаменталь шешімдері болып табылады.
Келтірілген Бессельдің бірінші текті функциясынан басқа Бессель теңдеуінің шешімі болатын функциялар да баршылық. Олардың ішінде
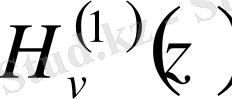 және
және
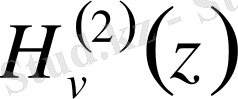 Ханкельдің бірінші және екінші текті арнайы функциялары болып табылады. Бұл функциялар Бессель теңдеуінің комплекс түйіндес шешімдері болып есептелінеді. Міне, сондықтан бұл функциялар Бессель теңдеуінің шешімдері болғандықтан, цилиндрлік функциялар ретінде мынадай:
Ханкельдің бірінші және екінші текті арнайы функциялары болып табылады. Бұл функциялар Бессель теңдеуінің комплекс түйіндес шешімдері болып есептелінеді. Міне, сондықтан бұл функциялар Бессель теңдеуінің шешімдері болғандықтан, цилиндрлік функциялар ретінде мынадай:
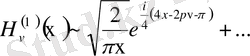 (*)
(*)
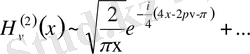 (**)
(**)
асимтотикалық өрнектермен беріледі, бұлардағы көп нүктелер қосылғыш
 -тың (
-тың (
 ) жоғарғы ретті аздық шама бар деп түсіндіріледі. Бұл (*) және (**) өрнектер жоғарыдағы
) жоғарғы ретті аздық шама бар деп түсіндіріледі. Бұл (*) және (**) өрнектер жоғарыдағы
 функцияның
функцияның
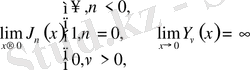 ,
,
асимтотикалық өрнектеріне байланысты,
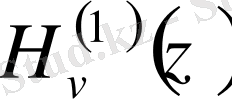 және
және
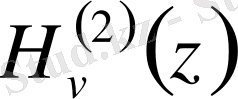 функциялары бірмәнді анықтайды. Бұл функцияларды нақты және жорамал бөліктерге ажыратып төмендегіше жазайық:
функциялары бірмәнді анықтайды. Бұл функцияларды нақты және жорамал бөліктерге ажыратып төмендегіше жазайық:
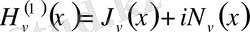 - бірінші текті Ганкель функциясы,
- бірінші текті Ганкель функциясы,
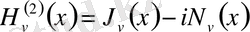 - екінші текті Ханкель функциясы,
- екінші текті Ханкель функциясы,
мұндағы
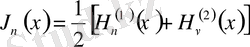
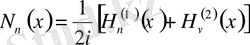
Ал бұл соңғы екі функциялар үшін
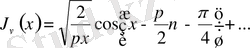
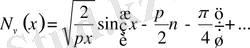
асимтоталық өрнектер орынды (бұлар (*) және (**) өрнектерден алынады) .
Егер бірінші текті Бессель функциялардың мәндерін пайдалансақ, онда
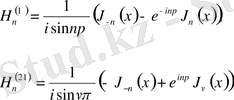
мұндағы
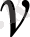 -бүтін емес; ал егер
-бүтін емес; ал егер
 бүтін болса, онда жоғарыдағы Лопиталь қағидасын қолдану керек.
бүтін болса, онда жоғарыдағы Лопиталь қағидасын қолдану керек.
Осылайша талдау арқылы төмендегі
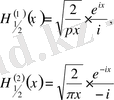
өрнектерін аламыз.
Ал бірінші және екінші текті Ханкель функцияларынан
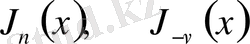 функцияларын анықтасақ, онда
функцияларын анықтасақ, онда
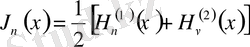 ,
,
түріндегі, кәдуілгі
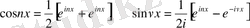
Эйлер формуласы секілді өрнектерді аламыз.
Интегралдық кескіні
Интегралдық өрнекпен бірінші рет Пуассон шұғылданған. Алдымен
 функцияны қатарға жіктеп, одан кейін Гамма және Бета функция байланыстарын
функцияны қатарға жіктеп, одан кейін Гамма және Бета функция байланыстарын
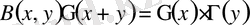 формуланы қолданып төмендегіше жазамыз:
формуланы қолданып төмендегіше жазамыз:
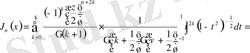
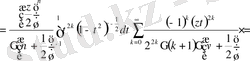 (0. 5)
(0. 5)
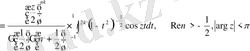 .
.
Егер біз
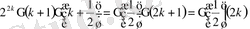
өрнегін пайдаланып және
 алмастыру енгізсек онда (0. 5) өрнекті
алмастыру енгізсек онда (0. 5) өрнекті
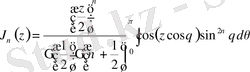 (0. 6)
(0. 6)
түріне келтіреміз. Міне бұл (0. 6) осы функцияның интегралдық өрнектерінің бірі деп қабылдауға болады.
Келесі түрін алу үшін комплекс анализдің мына
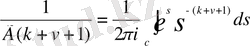
өрнегін пайдалансақ, онда
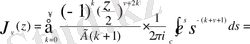
(0. 7)
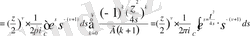
Егер z>0 деп және s= aлмастыру енгізсек, онда (0. 7) өрнектен
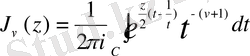 (0. 8)
(0. 8)
түрге келтіріледі, мұндағы
деп жоғарындағы С контур секілді. Бұл (0. 8) өрнeкті
 функциясының интегралдық өрнектерінің біреуі деп қабылдауға болады.
функциясының интегралдық өрнектерінің біреуі деп қабылдауға болады.
Егер (0. 8) формулаға алмастыру енгізіп, ондағы радиусты (шеңбердің) бірге тең деп алсақ, онда
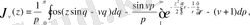
Ал бұған деп алмастырсақ, онда
 (0. 9)
(0. 9)
Мұнда Rez>0, v-кез келген сан.
Егер (0. 9) өрнекте
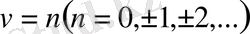 болса, онда оң жақтағы екінші қосылғыш нөлге тең болып, қарапайымданады.
болса, онда оң жақтағы екінші қосылғыш нөлге тең болып, қарапайымданады.
Осылайша талдаулар жасап Бессельдің екінші және үшінші текті функциялары үшін де интегралдық өрнектер алуға болады.
Мәселен, (0. 9) өрнекке
 және
және
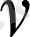 бүтін емес деп қабылдап
бүтін емес деп қабылдап
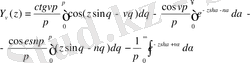
өрнекті аламыз. Ал, егер бұл өрнектің оң жағындағы үшінші интегралдағы
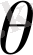 айнымалыны
айнымалыны
 айнымалыға алмастырсақ, онда қарапайым түрлендіруден кейін
айнымалыға алмастырсақ, онда қарапайым түрлендіруден кейін
 үшін
үшін
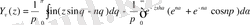 (0. 10)
(0. 10)
өрнегін аламыз.
Осы соңғы (0. 9) -(0. 10) формулалардан
 үшін мына Ханкель функциясы үшін интегралдық өрнекті
үшін мына Ханкель функциясы үшін интегралдық өрнекті
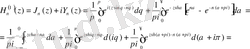
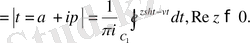
Осылайша
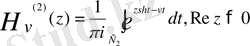 (0. 11)
(0. 11)
бұлардағы
Ханкель функцияларының қасиеттері:
Бірінші текті Бессель функциялары арқылы бейнеленуі:
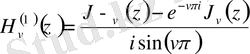
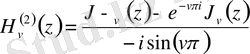
Вронский анықтауышы:
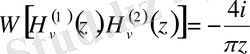
Индекстері бойынша симметриялы:
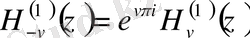
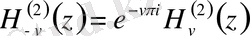
Асимптотикалық бейнеленуі:
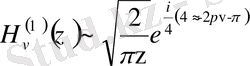 Equation. 3, если
Equation. 3, если
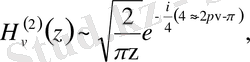 если
если
0. 3 Модифицирленген Бессель функциялары
А) бірінші текті модифицирленген Бессель функциялары
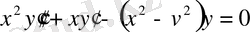 (0. 12)
(0. 12)
теңдеуі
 болғандағы (0. 2) теңдеудің дербес жағдайы, яғни
болғандағы (0. 2) теңдеудің дербес жағдайы, яғни
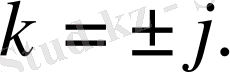 Оның дербес шешімі жорамал аргументті
Оның дербес шешімі жорамал аргументті
 функциясы түрінде жазылуы мүмкін.
функциясы түрінде жазылуы мүмкін.
Бірақ
 функциясын қарастырудың тиімсіздігі
х
-аргументтің нақты мәндерінде олар, жалпы айтқанда, комплекс мән қабылдайды. Мұны болдырмас үшін, мынадай функция енгіземіз:
функциясын қарастырудың тиімсіздігі
х
-аргументтің нақты мәндерінде олар, жалпы айтқанда, комплекс мән қабылдайды. Мұны болдырмас үшін, мынадай функция енгіземіз:
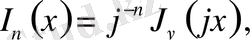
яғни х-тің нақты болғанда нақты мән қабылдайды. Шын мәнінде,
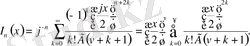
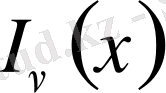 функциясы
жорамал аргументтің цилиндрлік функциясы
немесе
модифицирленген цилиндрлік функция
деп аталады.
функциясы
жорамал аргументтің цилиндрлік функциясы
немесе
модифицирленген цилиндрлік функция
деп аталады.
Б) екінші текті модифицирленген Бессель функциялары
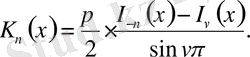
 болғанда шекке көшеміз:
болғанда шекке көшеміз:
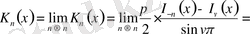
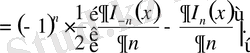
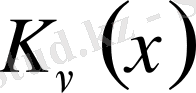 Equation. 3 функциясы
екінші текті модифицирленген функция
немесе
Макдональд функциясы
деп аталады.
Equation. 3 функциясы
екінші текті модифицирленген функция
немесе
Макдональд функциясы
деп аталады.
0. 4 Бурже функциясы
Бурже функциясы - бессельдік функциялардың интегралдық жалпыланған элементар функциялары болады. Ол фунцкияларды 1861 жылы Ж. Бурже енгізген. Ол мына түрде анықталады:
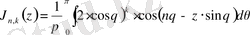
Дербес жағдайда, яғни k=0 болғанда Ангер функциясы келіп шығады.
0. 5 Біртекті емес Бессель функциялары дербес шешімдері
А) Ангер функциясы
Ангер функциясы - элементар функция емес, яғни біртекті емес Бессель теңдеулерінің дербес шешімі болып табылады:
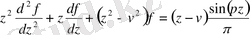
Ангер функциясының интегралдық өрнек түрінде бейнеленуі:
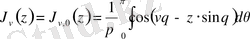
мұндағы
 Бурже функциясы.
Бурже функциясы.
Бүтін
 -дер үшін Ангер функциясы Бессель функциясымен беттеседі. Сондықтан Бессель функциясының анықтамасын бергенде, Ангер функциясына ұқсас, қысқартылған интеграл беріледі. Шынында да, бүтін емес
-дер үшін Ангер функциясы Бессель функциясымен беттеседі. Сондықтан Бессель функциясының анықтамасын бергенде, Ангер функциясына ұқсас, қысқартылған интеграл беріледі. Шынында да, бүтін емес
 -дер үшін олардың арасында айтарлықтай айырмашылық бар:
-дер үшін олардың арасында айтарлықтай айырмашылық бар:
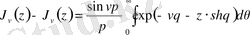
Вебер функциясымен ара қатынасы:
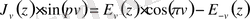 Equation. 3 .
Equation. 3 .
Б) Вебер функциясы
Вебер функциясы - біртекті емес Бессель теңдеулерінің дербес шешімі болып табылатын элементар емес функция:
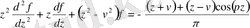
Вебер функциясының интегралдық өрнектелуі мына түрде болады:
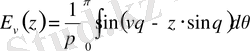
Ангер функциясымен ара қатынасы:
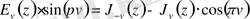
Бүтін
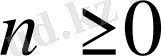 -дер үшін Вебер функциясының Струве функциясымен байланысты ара қатынасы:
-дер үшін Вебер функциясының Струве функциясымен байланысты ара қатынасы:
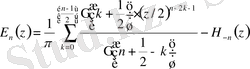
В) Струве функциясы
Струве функциясы - біртекті емес Бессель функцияларының дербес шешімдері болатын элементар емес функциялар болып табылады:
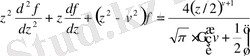
Струве функциясының интегралдық өрнектелуі мына түрде болады:
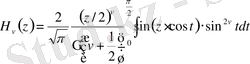
Қатарға жіктелуі мына түрде болады:
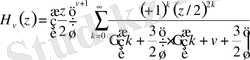
Модифицирленген Струве функциясы мына түрде жазылады:
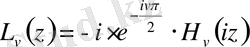
Г) Ломмель функциялары
Ломмель функциясы - біртекті емес Бессель функцияларының дербес шешімдері болатын элементар емес функциялар болып табылады:
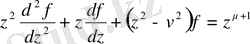
Бұл функцияны неміс математигі Эйген фон Ломмель енгізген.
Ломмель функциясының интегралдық өрнектелуі мына түрде белгіленеді:
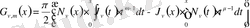
мұндағы
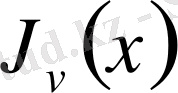 Equation. 3 - Бессель функциясы;
Equation. 3 - Бессель функциясы;
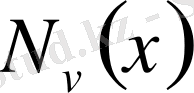 Equation. 3 - Нейман функциясы.
Equation. 3 - Нейман функциясы.
Ломмель функциясының қатарға жіктелуі мына түрде болады:
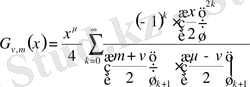 .
.
0. 6 Параболалық цилиндрлік функциялар ( Вебер функциясы)
Лаплас теңдеуі сияқты, Пуассон теңдеуі сияқты, Гельмгольц теңдеулері сияқты математикалық физиканың теңдеулері үшін параболалық цилиндрлік координаталар жүйесінде айнымалыларды ажырату әдісін пайдаланып алынатын дифференциалдық теңдеулердің шешімдері болып табылатын арнайы функциялар үшін жалпы атауы болып табылады.
Жалпы жағдайда цилиндрлік параболалық функциялары - келесі түрдегі теңдеулердің шешімдері болады
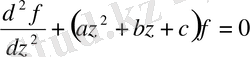 (0. 13)
(0. 13)
Осы теңдеулерге сызықты түрлендірулер жасасақ, онда келесі теңдеу пайда болады:
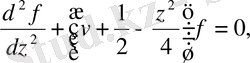
Яғни бұл теңдеудің шешімдері Вебер функциялары деп аталады және ол былайша белгіленеді
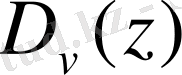 .
.
 ,
,
 ,
,
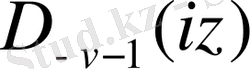 ,
,
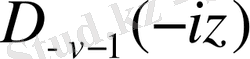 функциялары Вебер теңдеуінің шешімдері болып табылады, сонымен бірге бүтін емес
функциялары Вебер теңдеуінің шешімдері болып табылады, сонымен бірге бүтін емес
 үшін
үшін
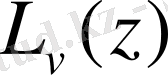 ,
,
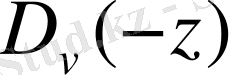 функциялары сызықты тәуелсіз.
функциялары сызықты тәуелсіз.
Барлық
 үшін
үшін
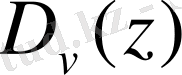 ,
,
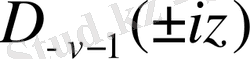 функциялары да сызықты тәуелсіз болады.
функциялары да сызықты тәуелсіз болады.
Практикада цилиндрлік параболалық функциялардың басқа да функциялары жиі қолданылады, (0. 13) теңдеуде
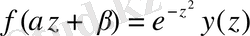 алмастыруын пайдаланып, Эрмит теңдеулерінің шешімі болатын Эрмит функцияларын қолданылады
алмастыруын пайдаланып, Эрмит теңдеулерінің шешімі болатын Эрмит функцияларын қолданылады
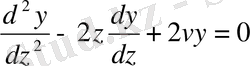 . (0. 14)
. (0. 14)
Эрмит функциялары келесі түрде белгіленеді
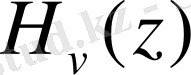 . (0. 14) теңдеудің жалпы шешімі мына түрде болады:
. (0. 14) теңдеудің жалпы шешімі мына түрде болады:
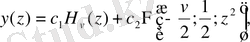
мұндағы
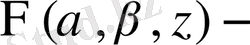 туындалатын гипергеометриялық функция.
туындалатын гипергеометриялық функция.
Теріс емес бүтін
 болғанда Эрмит функциясы Эрмит көпмүшелігімен беттеседі. Теріс бүтін
болғанда Эрмит функциясы Эрмит көпмүшелігімен беттеседі. Теріс бүтін
 болғанда Эрмит функциясы қателік функциялар арқылы тұйық түрде туындалады.
болғанда Эрмит функциясы қателік функциялар арқылы тұйық түрде туындалады.
Рекуррентті қатынастар
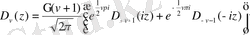
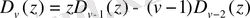
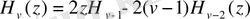
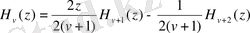
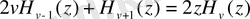
Дифференциалдау формулалары
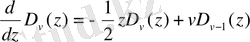
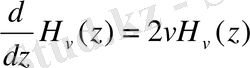
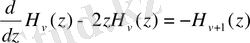
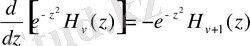
0. 7 Кельвин функциялары
Егер (0. 1) - дифференциалдық теңдеуде
 болса және x айнымалыны t-ға алмастырсақ, теңдікті t
бөліп, нәтижеде
болса және x айнымалыны t-ға алмастырсақ, теңдікті t
бөліп, нәтижеде
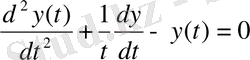 (0. 15)
(0. 15)
теңдеуді аламыз. Бұл теңдеудің бір-біріне сызықты тәуелсіз дербес шешімдері:
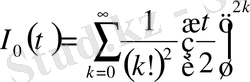 , (0. 16)
, (0. 16)
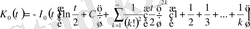
қатарлар болады.
Ал (0. 15) теңдеуге
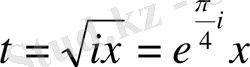 алмастыруын енгізсек, онда
алмастыруын енгізсек, онда
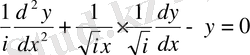
немесе
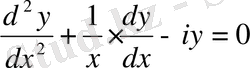
теңдеуді аламыз. Онда жоғарыдағы (0. 16) жеке шешімдер бойынша
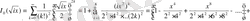
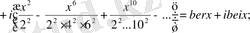
мұндағы
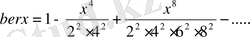
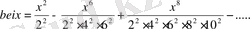
Дәл осылайша талдап, (0. 16) шешімді төмендегідей жазамыз:
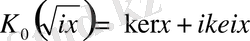 (0. 17)
(0. 17)
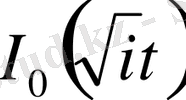 және
және
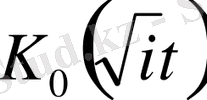 Бессель функцияларымен анықталады.
Бессель функцияларымен анықталады.
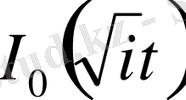 ,
,
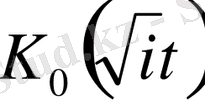 функциялары комплексті функциялар болады.
функциялары комплексті функциялар болады.
Олардың нақты және жорамал бөліктерін бөліп алсақ:
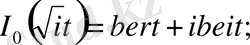
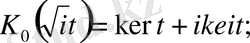
ber және bei ker және kei белгілеулерін Кельвин енгізді.
Кельвин функцияларының бірқатар қатынастар бар; олардың кейбіреулерін біз дәлелдеусіз келтіреміз:
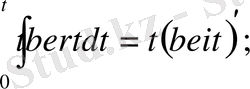
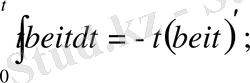
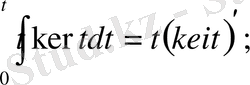
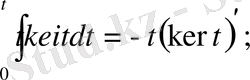
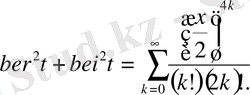
Егер жоғарыдағы Бессель теңдеуіне
 қабылдағандағы шешімдерін
қабылдағандағы шешімдерін
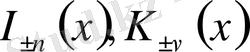 деп қабылдасақ, онда олар арасында
деп қабылдасақ, онда олар арасында
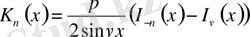
өрнекті аламыз. Бұл өрнекті Макденольд функциясы деп атаймыз.
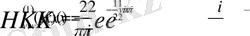
өрнегіне
 деп алсақ, онда
деп алсақ, онда
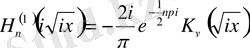
теңдікке келеміз.
Егер бұларда
 болса, онда
болса, онда
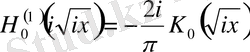
Ал
 комплекс функция болғандықтан оны
комплекс функция болғандықтан оны
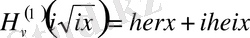
деп қабылдасақ, онда
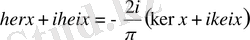
Бұл комплекс функциялардың сәйкес нақты және жорамал бөліктерін теңестіріп
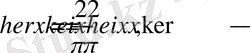
теңдіктерін аламыз.
1 Бессель теңдеулері
1. 1 Бессель теңдеулері
Дифференциалдық теңдеулер теориясынан, шешімдері элементар функциялар интегралының ақырлы сандар көмегімен өрнектеле алмайтын теңдеулер бар болатыны, белгілі, яғни ондай теңдеулер квадратурада өрнектеле алмайды. Оларға жоғарғы математиканың жалпы курсында қарастырылатын Риккати теңдеуі
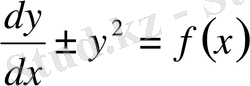
жатады.
Қосымшаларда көбінесе, шешімдері элементар функциялардың ақырлы санымен анықтала алмайтын дифференциал теңдеулер жиі кездеседі, яғни шешімдері бар, бірақ шешімдерді қандай да бір жинақталатын дәрежелік қатарлар түрінде өрнектеледі. Осындай теңдеулердің бірімен біз қазір танысамыз.
Анықтама . Бессель теңдеуі деп коэффициенттері айнымалы болатын, мынадай екінші ретті сызықты дифференциал теңдеуді айтамыз:
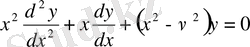 (1. 1)
(1. 1)
Немесе
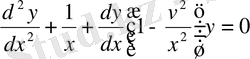 .
.
(1. 1) теңдеу сызықты болғандықтан, онда оның жалпы шешімі мына түрде жазылады:
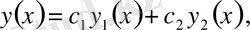
Мұндағы
 және
және
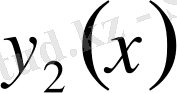 - екі тәуелсіз дербес шешімдер, ал
- екі тәуелсіз дербес шешімдер, ал
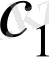 және
және
 - тұрақты шама.
- тұрақты шама.
(1. 1) теңдеудің шешімі Бессель функциясы немесе цилиндрлік функциялар деп аталатын арнайы функцияларды береді.
Теңдеуге енетін
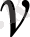 саны тұрақты шама болады. Ол (1. 1) теңдеудің
индексі
деп аталады, сонымен бірге
сәйкес цилиндрлік функцияның
реті
немесе
индексі
деп аталады.
саны тұрақты шама болады. Ол (1. 1) теңдеудің
индексі
деп аталады, сонымен бірге
сәйкес цилиндрлік функцияның
реті
немесе
индексі
деп аталады.
Осылайша, әрбір
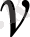 мәніне өзінің
мәніне өзінің
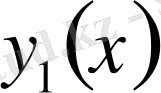 және
және
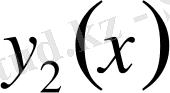 жүйесі сәйкес келеді.
жүйесі сәйкес келеді.
(1. 1) дифференциалдық теңдеуге көптеген физикалық құбылыстарды сипаттайтын теңдеулер келтіріледі: Негізінде, (1. 1) теңдеуді 1766 жылы дөңгелек лембрананы зерттеу кезінде Л. Эйлер дәлелдеген. Шындығында,
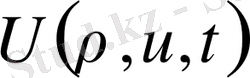 функциясы, яғни t уақыт моментіндегі мембрананың орнын анықтайтын функциясы цилиндрлік координата жүйесінде қарастырылатын толқындық теңдеуді қанағаттандырады:
функциясы, яғни t уақыт моментіндегі мембрананың орнын анықтайтын функциясы цилиндрлік координата жүйесінде қарастырылатын толқындық теңдеуді қанағаттандырады:
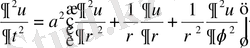
Сонымен қатар, оны Фурье әдісімен шешу кезінде Бессель функциясына келтіріледі. Міне осыдан, (1) теңдеудің шешімінің - цилиндрлік функция аталуы шыққан.
(1. 1) теңдеуі - немістің математигі және астрономы, яғни 1824 жылы цилиндрлік функциялар теориясын жүйелі түрде мазмұндаған, Бессельдің аты бойынша аталған. Бірақ, бұл атау онша дұрыс емес, ақталмайды, себебі Бессель функциялары бұған дейін Д. Бернулли және Л. Эйлер жұмыстарында кездескен болатын.
1. 2 Бессель теңдеуінің шешімдері. Бірінші текті Бессель функциясы
Енді (1. 1) теңдеудің шешімін табамыз. Ол үшін, дифференциал теңдеулер теориясынан кейбір ұғымдар керек болады, біз оларды дәлелдеусіз келтіреміз.
Мына теңдеу берілген болсын:
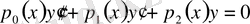 (1. 2)
(1. 2)
Мұндағы
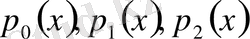 коэффиценттері
х
- ке қатысты көпмүшеліктер,
коэффиценттері
х
- ке қатысты көпмүшеліктер,
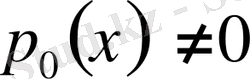 . Сонда осы теңдеудің шешімі бүтін, теріс емес
х-
тің дәрежелері бойынша жинақталатын дәрежелік қатармен өрнектеледі, яғни мына түрдегі қатар бойынша :
. Сонда осы теңдеудің шешімі бүтін, теріс емес
х-
тің дәрежелері бойынша жинақталатын дәрежелік қатармен өрнектеледі, яғни мына түрдегі қатар бойынша :
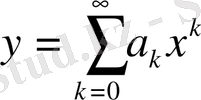 (1. 3)
(1. 3)
(1. 3) формуладағы
 коэффиценттерді, мысалы, (1. 3) қатарды (1. 2) теңдеуге қойып және табылған теңдіктің сол жағындағы
х
- тің әртүрлі дәрежесіндегі коэффиценттерді нольге теңестіру арқылы анықтаймыз.
коэффиценттерді, мысалы, (1. 3) қатарды (1. 2) теңдеуге қойып және табылған теңдіктің сол жағындағы
х
- тің әртүрлі дәрежесіндегі коэффиценттерді нольге теңестіру арқылы анықтаймыз.
Егер
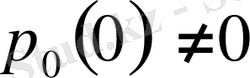 , болса, онда (1. 2) теңдеудің шешімін
, болса, онда (1. 2) теңдеудің шешімін
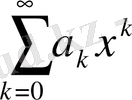 қатары түрінде іздей аламыз, себебі
қатары түрінде іздей аламыз, себебі
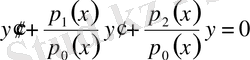
теңдеуінің коэффиценттерін (1. 2) теңдеудің екі жағына да
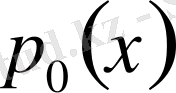 - ке бөлгеннен соң алынған коэффиценттер енді
x
=0 болғанда үзіліссіз емес (болмайды) . Бұл келеңсіздіктен шығу мүмкін болады, егер (1. 2) теңдеудің шешімі қарастырылып отырған жағдайда, жалпыланған дәрежелік қатар түрінде іздеу керек болса,
- ке бөлгеннен соң алынған коэффиценттер енді
x
=0 болғанда үзіліссіз емес (болмайды) . Бұл келеңсіздіктен шығу мүмкін болады, егер (1. 2) теңдеудің шешімі қарастырылып отырған жағдайда, жалпыланған дәрежелік қатар түрінде іздеу керек болса,
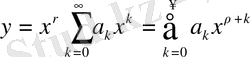
яғни кәдімгі дәрежелік қатардан айырмашылығы тек
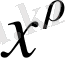 көбейткішінде ғана. Мұнда
көбейткішінде ғана. Мұнда
 бүтін болуы міндетті емес, теріс сан болуы да мүмкін.
бүтін болуы міндетті емес, теріс сан болуы да мүмкін.
Бессель теңдеуіне қайта оралайық.
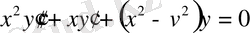 (1. 1
/
)
(1. 1
/
)
Мұнда
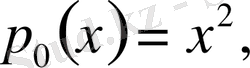 және
және
 болғанда, бұл коэффицент нольге айналады. Сондықтан, (1. 1
/
) теңдеудің жалпыланған дәрежелік қатар түріндегі шешімін тауып көрейік:
болғанда, бұл коэффицент нольге айналады. Сондықтан, (1. 1
/
) теңдеудің жалпыланған дәрежелік қатар түріндегі шешімін тауып көрейік:
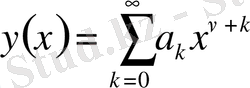 (1. 4)
(1. 4)
Сонда
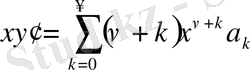 ;
;
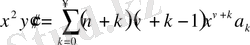 ;
;
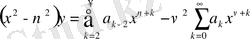 .
.
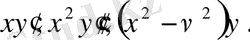 -мәндерін (1. 1
/
) теңдеудің сол жағына қойып және
х
- тің әртүрлі дәрежесіндегі коэффиценттерді нольге теңестіріп:
-мәндерін (1. 1
/
) теңдеудің сол жағына қойып және
х
- тің әртүрлі дәрежесіндегі коэффиценттерді нольге теңестіріп:
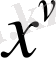
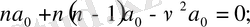
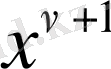
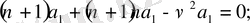
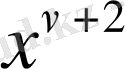
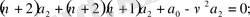
. . .
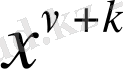
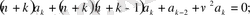
. . .
Немесе
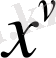
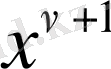
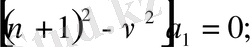
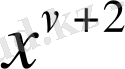
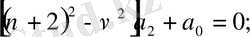
. . .
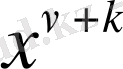
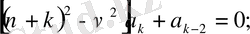
. . .
 -ны анықтау үшін алынған шексіз теңдеулер жүйесі екі жүйеге тарайды: біріншісі - тақ индексті
-ны анықтау үшін алынған шексіз теңдеулер жүйесі екі жүйеге тарайды: біріншісі - тақ индексті
 коэффиценттері үшін, екіншісі - жұп индексті коэффициенттер үшін:
коэффиценттері үшін, екіншісі - жұп индексті коэффициенттер үшін:
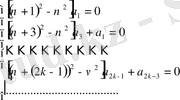
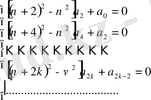
Бірінші жүйенің шешімдері қатар коэффиценттерінің нольдік мәндері болады:
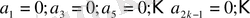
Екінші жүйеде
 - ді кез келген етіп, таңдамай алса болады, сонда
- ді кез келген етіп, таңдамай алса болады, сонда
 коэффициенттері
коэффициенттері
 арқылы бірмәнді өрнектеледі, егер
арқылы бірмәнді өрнектеледі, егер
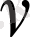 - бүтін теріс емес сан болмаса:
- бүтін теріс емес сан болмаса:
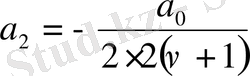 ;
;
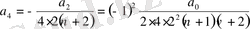 ;
;
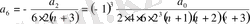 ;
;
. . .
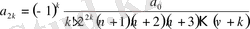 ;
;
. . .
Табылған
 мәндерді (4) -ке қоямыз. Сонда Бессель теңдеуін қанағаттандыратын, мынадай қатар аламыз:
мәндерді (4) -ке қоямыз. Сонда Бессель теңдеуін қанағаттандыратын, мынадай қатар аламыз:
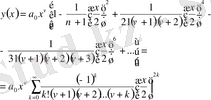 (1. 5)
(1. 5)
Бұл қатар
 -дің оң болғандағы және теріс болғандағы мәндерінде де (1. 1) теңдеуді қанағаттандырады. Жарамсыз жағдайы тек
-дің оң болғандағы және теріс болғандағы мәндерінде де (1. 1) теңдеуді қанағаттандырады. Жарамсыз жағдайы тек
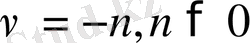 болғанда.
болғанда.
Негізінде,
 болғанда,
болғанда,
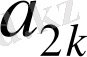 коэффиценттерін табатын алгебралық теңдеулер жүйесі шешілмейтін болып қалады. Сондықтан (1. 5) қатары,
коэффиценттерін табатын алгебралық теңдеулер жүйесі шешілмейтін болып қалады. Сондықтан (1. 5) қатары,
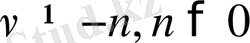 болғандағы, яғни
болғандағы, яғни
 -дің бүтін оң және бөлшек мәндеріндегі (1. 1) теңдеудің шешімін анықтайды.
-дің бүтін оң және бөлшек мәндеріндегі (1. 1) теңдеудің шешімін анықтайды.
 индексіне сәйкес мәніндегі Бессель теңдеуінің шешімін
индексіне сәйкес мәніндегі Бессель теңдеуінің шешімін
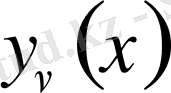 арқылы белгілейміз.
арқылы белгілейміз.
Осылайша,
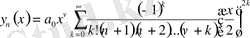
Енді Бессель теңдеуінің шешімінің анықталу облысын табамыз. Бұл (1. 5) қатардың жинақты болғандағы х мәндерінің жиыны болатыны, анық. (1. 5) дәрежелік қатар х - тың кез келген мәнінде жинақты болады, бұған Даламбер белгісі бойынша оның жинақтылық радиусын анықтап, оңай көз жеткізуге болады:
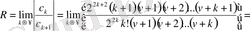
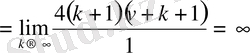
Жинақтылық радиусы шексіздікке тең болғандықтан, (1. 5) қатардың жинақтылық облысы барлық сандық ось болады. Зерттеліп отырған дәрежелік қатар өзінің жинақтылық облысында бірқалыпты жинақталады.
(1. 5) қатардың жалпы мүшесі үшін өрнегіне
 тұрақты шамасы кіреді.
тұрақты шамасы кіреді.
 ретінде кез келген санды алуға болады. Бессель теңдеуінің шешімін анықтайтын қатардың жалпы мүшесі жинақты формада жазылатындай етіп
ретінде кез келген санды алуға болады. Бессель теңдеуінің шешімін анықтайтын қатардың жалпы мүшесі жинақты формада жазылатындай етіп
 - ді таңдап алуға болады ма? Әрине, болады екен. Ол үшін бізге гамма-функция үшін келтіру формуласы көмектеседі.
- ді таңдап алуға болады ма? Әрине, болады екен. Ол үшін бізге гамма-функция үшін келтіру формуласы көмектеседі.
Шынында да,
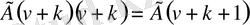
Егер енді (1. 5) қатардың жалпы мүшесіндегі бөлшектің бөлімін
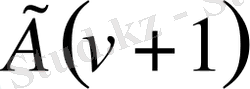 ге көбейтсек, онда мынаны аламыз:
ге көбейтсек, онда мынаны аламыз:
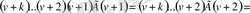
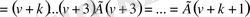
Бұдан, осы бөлшектің бөлімін
 -ға көбейтейік, өйткені
-ға көбейтейік, өйткені
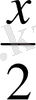 айнымалысын бір дәреже таңбасының астына жазуға болар еді.
айнымалысын бір дәреже таңбасының астына жазуға болар еді.
Ендеше,
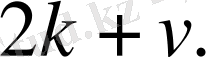 ретінде мына өрнекті таңдаймыз:
ретінде мына өрнекті таңдаймыз:
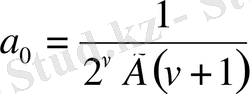
Сонда (1. 5) қатардың орнына мына түрдегі қатарды аламыз:
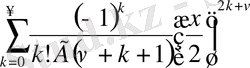
Анықтама. Мына қатармен анықталған функция,
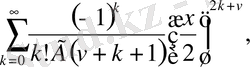
яғни
x
-тің кез келген мәнінде жинақталатын,
 индексті бірінші текті
Бессель функциясы
деп аталады.
индексті бірінші текті
Бессель функциясы
деп аталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz