Нақты газдардың идеалдықтан ауытқуы: молекулалық өзара әрекеттесу, Ван-дер-Ваальс теңдеуі және фазалық өтулер


НАҚТЫ ГАЗДАР
Клапейрон - Менделеев теңдеуі жуықталған тендеу болып табылады. Ол жеткілікті төмен қысымдар кезінде орындалады жоне де қысым неғүрлым аз болса, оның орындалу дәлдігі солғүрлым жоғары. Қьісым артқан кезде, Кла-пеЙрон-Менделеев тендеуінің салдары болып табылатын Бойль-Мариотт, Гей-Люссак зандары тәріздІ газ заңдарынан ауытқулар арта түседі екен. Бүған таңғалатындай ештеңе жоқ, ол үшін идеал газдарға өткен кездерде қандай ескермеушіліктерді жібергенімізді еске түсірсек жеткілікті. Біз идеал газды өзара әрекеттеспейтін молекулалардан түратын газ деп алдық, ал молекула-лардың өздері материалдық нүктелер болып табылады дедік, яғни біз олар-дық молшерлерін (колемдерін) ескергеніміз жоқ. Шын мөнісінде молекула-лардың меншікті көлемдері де, олардың арасында өзара өрекеттесу күштері де бар. Бүлар әсіресе газдың қысымы жоғарылап, молекулалар тығызырақ орналасқан кезде күштірек біліне бастайды.
4. 1. Газдың қасиеттерінің идеалдықтан ауытқуы
Төменде келтірілген кестеде Ы 2 азоттыңбір молініңалатын V көлемінің түрліше р қысымдар және 0"С температура кезіндегі төжірибеде алынған мондері және рҮ көбейтіндісінің мәндерІ келтірІлген. Осы кестеден көріп отырғанымыздай, 100 атм қысым кезінде-ақ V колемнің мөнінің теорялық мәннен 7% айырмашылығы бар екендігін көреміз. Қысым одан өрі артқан кезде газдың көлемі Клапейрон-Менделеев тендеуі бойынша есептелген мәннең алшақтай түседі де, 1000 атм қысым кезіндегі газдың көлемі идеал газ күйі теңдеуі беретін мәннен екі есе артык болады. Клапейрон-Менделеев тендеуі бойынша барлык қысымдар кезінде түрақты болып қалатын^К кобейтіндісі де осындай жағдайда. Қысым жоғарылаған кезде бүл көбейтіндінің мөні де артып отырады. (кесте)
Азоттың бір молІнің түрліше қысымдар кезіндегі көлемі
р, атм V, 10*У рУ\0 л атмм ъ р, атм У\0\м ъ рУ\О 4 атмм г
1 224 224 700 0, 532 372 100 2, 4 240 900 0, 483 437 300 0, 85 255 1000 0, 460 461 500 0, 625 322
Осы келтірілген мәндерге қарайтын болсақ, жеткілікті үлкен қысымдар кезінде нақты газдардың сырткы күштің әсерінен Клапейрон-Менделеев тең-деуінен күтетінімізге карағанда кош аз сығылатындығын көреміз.
Газ колемінің қысымға осы келтірілген емес, сапалық та сипаттары болады екен. Бүл аса маңызды сапалық сипаттар жеткілікті жоғары қысымдар мен сәйкес температуралар кезінде білінеді.
Әрбір газға тән белгілі бір температура болады (Бойль температурасы), осы температура кезіндерК көбейтіндісі қысымның қайсы-бір интервалын-да қысымға тәуелсіз болады, яғни бүл температурада газ Бойль-Мариотт заңына бағынады.
Қысымның және температураның белгілі мәндері кезінде газдар кокден-сациялакады, яғни сүйық күйге өтеді. Бүл күбылысты идеал газ күйінің тең-деуінен шығарып алу мүмкін емес.
Енді осы процесті тередірек қарастырайық.
4. 2., Молекулалар аралык күштер. Идеал газ зандарынан ауытку
I. Идеал газ заңдары - жуықталған заңдар. Олардан ауытқулардың сандық та, сапалық та сипатгары бар. Сандық ауытқуларға келсек, Менделеев-Юіапей-рон теидеуірГ=. #Гнақты газдар үшін тек жуықталып қана орындалады. Ал са-палық ауытқуларға келсек, оның сипаты тереңІрскте жатыр. Нақты газдарды сүйық жоне қатты күйлерге откізуге болады. Ал егер газдар Менделеев-Клапей-рон тендеуіне катал бағынатын болса, онда бүл мүмкін болмаған болар еді.
Идеал газ заңдарынан ауытқулар газ молекулаларының арасында идеал газ теориясында ескерілмеген күштердің әсер етуімен байланысты. Бүл күштердің химиялық қосылыстардың пайда болуына әкелуі мүмкін. Бүл жағ-дайда олар химиялыц немесе валенттік куштер деп аталады. Егер химиялық қосылыстар пайда болмайтын болса, онда молекулалардың жөне атомдар-дың арасындағы өзара өрекеттесу күштері молекулалыц күштер деп атала-ды. Біздің бүл жерде тоқталатынымыз тек нейтрал атом және молекулалар арасындағы молекулалық күштер ғана болып табылады.
2. Алыс қашықтықтарда молекулалык күштер тартылыс күштері болып табылады. Бүл тартылыс күштерІн нақты газдардың молекулалық теориясы-ның негізін қалаған голланд ғалымының есімімен Ван-дер-Ваальс (1837-1923) куштері деп атайды. Түтастай алғанда электр нейтрал болатын, элементар зарядтардан түзілген бүл күрделі болшектердің арасында тартылыс күштері қалай пайда болуы мүмкін? Мүны түсіну үшін екі жағдайға назар аудару ке-рек. Біріншіден қарама-карсы зарядтар белшек ішінде бір нүктеде жинақтал-маған. Осының арқасында олардың сырткы орісі өшпейді - кезкелген атом немесе молекуланың төңірегінде қашықтық артқан кезде жеткілікті тез өшстін электр өрісі болады. Екіншіден, сыртқы өрістің әсерінен молекула ішіндегі за-рядтардың орны немесе қозғалысы оң зарядтар өріс бағытында, ал теріс заряд-тар - қарсы бағытта ығысатындай болып, сәл-пәл өзгереді. Бүл қүбылыс электр поляризациясы деп аталады. ЕндІ бір-бірінен өте азғантай қашықтықта орна-ласқан 1 және 2 күрделі нейтрал бөлшектерді қарастырайык; әлі де болса, Е, ерісініңмәні назар аударалықтай болсын. Осы Е, орістің өсерінен 2 болшек полярланады, сейтіп оның бірінші бөлшек түрған жердегі Е 2 элекгрөрісікүшейеді. Е 2 өрістің әсерінен бірінші бөлшек те полярланады да, бүл да Е, өрістің күшеюіне өкеп тірейді және т. с. с. Осылардың нәтижесінде бөлшектер бір-біріне қарама-қарсы зарядталған бүйірлерімен бүрылып түратын болады. Олар бір-біріне қарама-қарсы полгостерімен қарап түрған магниттер тәрізді тартылатын болады. Қара-стырылған күштер дисперсиялық куштер деп аталады.
Дисперсиялық күштермен катар газ молекулалары арасында диполдік-ба-гытталгыш күштер де өсер ете алады. Бүлар да тартылыс күштері, тек олар дисперсиялық күштерден әлсіз болады. Сонымен қатар, диполдік-бағытгал-ғыш күштер газдың температурасына тәуелді болады. Олар газ молекулала-ры сыртқы электр орісі жоқ кездін, өзінде-ақ полярланған кезде пайда бола-ды. Мүндай молекулалар полярлық деп аталады. Сыртқы электр өрІсІнде по-лярлық молекулалар магнит ерісіндегі магнит тілшікгерІ тәрізді бүрылады. Енді өзара әрекеттесетін екі полярлық молекуланы көзге елестетейік. Бір молекуланың электр өрісіндегі екінші молекула бүрыла бастайды. Молекула-лар өздерінің қарама-қарсы зарядталған жақтары бір-біріне қарап түратын-дай болып бүрылады. Осының нәтижесінде тартылу пайда болады. Бағдар-лануды жылулық қозғалыс үнемі бүзып отыратындыктан, диполдік-бағдар-лағыш күштер газ температурасына тәуелді болуы тиіс.
Егер молекулалардың ара қашықты олардың мелшерлерімен салыстыр-ғанда үлкен болатын болса, онда дисперсиялық және диполдық-бағдарлағыш күштердің қашықтықтың жетіншІ дәрежесіне кері пропорционал болатын-дығын дәлелдеуге болады екен. Бірақ бүл деректі біз еш жерде қолданбай-мыз, сондықтан ол жайлы тек сөз етіп кана кетіп отырмыз.
Өзара өрекеттесетін бөлшектердің электрондық қабықшалары бір-біріне еніп кететіндей жуық қашықтықтар кезінде, молекулалық тартылыс күштері тебілу күшіне айналады. Кванттық механикаға сүйенетін теория өзара өре-кеттесетін бөлшектердің ара қашықтығы азғантай болатын кезде, тебілу күштерінің аса зор болатындығын көрсетеді. Бүл күштер қашықтық артқан кезде тез азаяды. Қашықтық өзара әрекеттесетін бөлшектердің диаметрінен асқан кезде, тебілу күші қа
шықтық артқан сайын экспонента түрінде өшеді.
3. Молекулалардың өзара әрекеттесуІн ІДх) өзара әрекетгесу потенциалдық энер-гиясымен сипаттаған ыңгайлы, бүл фнукция өзара жақындаған молекулалардың центр-лерінің х ара қашықтығына тәуелді. Айты-лып кеткендерге сай 13(х) функцияның түрін жобалап 4. 1-суреттегідей түрде беруге бола-ды. Оның минимумы бар, онда тартылыс күштері тебілу күштерімен теңгеріседі.
Газдар теориясының көптеген мәселеле-рінде 1_І(х) функциясы үшін
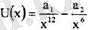
жуықталуын пайдаланады, мүндағы а, және а 2 - түрақтылар. Бүл функция Леннард-Джонс потенциалы деп аталады. БіріншІ мүше тебілу күштеріне, ал екінші мүше - Ван-дер-Ваальс тартылыс күштеріне сәйкес келеді. Тартылыс күштері қашықтықтың жетінші дәрежесіне кері пропорционал болады (себебі
Ғ = -<Ю/с1х) . Бірінші мүше жай ғана жуықталу деп қарауға болады.
Ван-дер-Ваальстың күй теңдеуі теориясындағы жуықталу бойынша, ІДх) функциясының графигіндегі сол жақтағы тік дерлік котерілетін учаскесІ вер-тикал түзумен алмастырылады. Егер сі осы түзуден координаттар басына дейінгі кашықтық болса, онда озара орекеттесуші бөлшектердің центрлері қашықтықтан кіші қашықтыққа тең бола алмайды, олар бүдан жақынырақ жерге ксле алмайды. Қарастырылып отырған жуықталу арасында тартылыс күштері осер ететін серпІмді қатты шарлар моделіне сәйкес келеді. Осы мо-делді біз алда да пайдаланамьгз. Тебілу күштерін ескеру арқылы біз шарлар-дың молшерлерін шектеулі деп санаймыз. Бүл күштср тек соқтығысулар кез-інде ғана пайда болады. сІ қашықтық молекулаиың диаметрі рөлін атқарады.
4. 3. Ван-дер-Ваальс теңдеуі
Жоғары қысымдар кезіндегІ газдардың касиеттерін және сұйық-газ фаза-лық өтуіи Мендлеев-Клапейрон теңдеуі сипаттай алмайды, бүл тендеу тек томенгі қысымдар кезіндегі газдар үшін ғана орындалады екен. Бірақ бүл тең-деуді нақты газдардың кезкелген қысымдар кездегі смпатгарын ғана емес, со-нымен катар жеткілікті дәлдікпен сүйықтардың касметтерін жөне газ күйінен сүйық күйге фазалық өтуді де сііпатгай алатын түрде түзетуге болады.
Бүл үшін газ молекулалары дегеніміз ешқандай мөлшерлері жоқ материалдық нүктелер деген көзқарастардан және молекулалар арасында ешқандай өзара әрекеттесу жок деген тоқтамнан бас тарту керек. Егер шындығында да молекулалар аралық күштер бар деп және молекулалардың белгілі мөлшер-лері болады деп алатын болсак және Мендлеев-Клапейрон тендеуіне қажетгі түзетулерді енгізетін болсақ, онда тәжірибе нәтижелерімен жақсырақ үйлесімді болатын нақты газдардың жаңа күй теңдеуін алуға болады деп үміттенуге болады.
Молекулалардың молшерлері де, молекулалар арарсындағы өзараәрекет-тесу күштері де ескерілген жаңартылған күй теңдеуін 1873 жылы Ван-дер-Ваальс үсынды және ол қазір оның есімімен аталады.
Айта кететін нәрсе, қарастырғалы отырған нақты газдардың күй теңдеуі де жуықталған тендеу, себебі молекулалардың арасындағы озара өрекеттесу күштерін дәл есептеу әлі де мүмкін болмай отыр.
Идеал газдың бір молі үшін жазылған
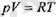
күй теңдеуінде V деп газ түрған ыдыстың колемін түсшеміз. Екінші жағынан онда қозғалып жүрген газ молекулаларынын, кезкелгенінің кезкелген жерде бола алатын көлемі, себебі идеал газдьтң материалдық нүкте-молекулалары үшін ыдыстың кезкелген жері бос, әр молекула үшін ыдыста одан басқа мо-лекула жоқ тәрізді. Шындығында газда ыдыстың барлық көлемі молекулалар үшін бос емсс, себебі әр молекула белгілі келем алып түр және ыдыстың бүл болігінде басқа молекулалар бола алмайды.
Бүл жағдайды ескеру үшін ыдыстың көлемінен молекулалар қозғала ал-майтын, олардың оздері алып түрған колемін алып тастау керек. Оны Ь деп белгілейік. Сонда (3. 1) тендеу мына түрде жазылады:
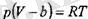
мүндағы Ь түзету газдың қысымды шексіз артгырған кезде ( газ молекулала-рын әбден тығыздаған кезде) алатын шектік көлемі. Шындығында да (4. 3) теңдеуді
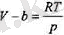
түрінде жазып, р - «> кезінде колемнің V = Ь болатындығын көреміз. Ь мөні : Ъ = {\6ІЪ) жг 2 М 0 , мүңдағы Л^-Авогадросаны.
Ъ түзетуді енгізу аркылы ескерілген молекулалардың меншікті көлемімен катар тағы да молекулалар арасындағы тартылыс күштері де бар. Бүл күштердің өсерінен газ молеі^лаларының кезкелген ауданшаға, мысалға, кысымы кезкелген бірдей жағдайларда идеал газға карағаңда азырақ болады.
Шындығында да, ыдыстың қабырғасына жуық орналасқан кезкелген мо-лекуланың бір жағындагы "көршілері" екінші жағындағы "көршілерінен" артык, болады да, оған түсірілетін басқа молекулалар тарапынан пайда бола-тын қорытқы тартылыс кұші басы артық молекулалар саны бар жағына қарай, яғни ыдыстыц Ішіне қарай бағытталады. Осының арқасында ыдыстың қабы-рғасына түсірілетін кысым қайсы-бір Др шамасына кем болады. Сөйтіп, қысым үшін (4. 4) ернектің орнына мынандай өрнекке келеміз:
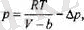
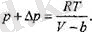
немесе
Молекулалардың арасындағы тартылыс күші сларды өзара жақындатуға тырысады. Сыртқы қысым да дәл осылай әсер етеді.
Енді осы қосымша қысымның неге тәуелді болатындығын қарастырайық.
Ыдыс қабырғасына жуык қабатқа газ молекулалары тарапынан болатын қысымның осы қабаттың бірлік ауданына келетін барлық молекулаларға әсер ететін кұшке тсң болатындығы анык. Бүл күштің молекулалардың п тығыз-дығына тәуелдІ болатыны анық. Екінші жағынан, қабырғаға жуық қабаттағы тартылысқа үшыраған молекулалар саны да п санына пропорционал болады.
Демек, Ар - гг , п шамасы газдың бір молінің алатын көлеміне кері пропорционал болатындықтан, Ар - аІУ 2 , мүндағы Ғгаздың молдік келемі де, ал а- пропорционалдық коэффицкенті, оның сан мәні молекулалардың арасын-дағы тартылыс күшінің сипатына тәуелді болады.
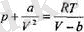
Сонымен, газдың қысымы үшін өрнекті молекулалар арасындағы тарты-лыс күшін ескере отырып, былайша жазуға болады екен:
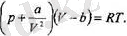
осыдан
Газдың қысымын, колемін және температурасын байланыстыратын бүл теңдеу нацты газдың күй теңдеуі болып табылады.
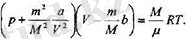
Мүнда т- газдың массасы, М ~ оның молдік массасы, V- газдың алып түрған көлемі.
(3. 3) тендеу газдың молі үшін жазылған. Газдың кезкелген мөлшері үшін оны мына түрде жазуға болады:
Тығызырақ газдар үшін Ван-дер-Ваальс теқдеуі сандық қатынас ретінде жарамайды. Бірақ сапалық жағынан ол мүндай газдардың да төуір сипатта-масын береді. Сондықтан заттың сапалық сипаттамаларын зерггеу үшін Ван-дер-Ваальс теңдеуін кысымдар мен температуралардың барлык өзгеріс аума-ғында да қолданатын боламыз. Бүл жағдайда оны жуыцталган жартылай змпирикалық теңдеу деп қарастыруымыз керек. Ван-дер-Ваальс тендеуіне толық бағынатын газдарды Ван-дер-Ваальс газдары деп атайды.
4. 4. Ван-дер-Ваал ьс газының нзотермалары
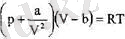
тендеудің екі жағында ү 2 -қа көбейтеміз. Жақшаларды ашқаннан кейін юо-терманың түрі
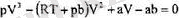
Ван-дер-Ваальс газьшың изотермаларын кезкелген температураларда қарастыру үшін
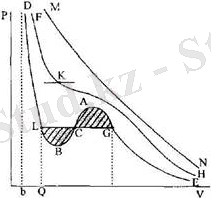
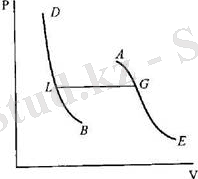
болады. Бүл V бойынша үшінші дөрежелі теңдеу, бүған р қысым параметр ретінде кІреді. Коәффициенттері нақты, заттық болатындықтан, теңдеудің бір заттық түбірі, немесе үш түбірі болады. Әрбір түбірге (р, У) жазықтығында р=сопзі изобараның изотерманы қиып өтетін нүктесі сөйкес келеді. Бір түбір болатын бірінші жағдайда қиылысу нүктесі де біреу болады. Бүл жағдай тем-ператураның жеткілікті жоғары болуына сәйкес келеді. Изотерма монотонды түсіп келе жатқан МЫ қисығы түрінде болады (4. 2-сурет) . Төменірек темпе-
ратуралар кезінде және р қысымның белгілі мондерінде (4. 8) теңдеудің
УрУ^. Уз үш түбірлері болады. Мүндай кездерде изобара изотерма-ны үш Ь, С, С нүктелерінде қиып өтеді (4. 2-сурет) . Изотерманың өркештенген ЬВСАО учаскесі бар. Ол әуелі монотонды түседі ( ВВ учас-ке), сосын ВА учаскеде монотонды көтеріледі, ал содан соң А нүктеден кейін тағыда монотонды түседі. Қайсы бір аралык температура кезін-
де барлық үш V,, У 2 , V-, түбірлер те-
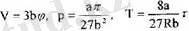
деп табамыз. Осы өрнектерді Ван-дер-Ваальс тендеуіне қойғаннан кейін ол
ңеседі. Мүндай температура және оған сәйкес келетін изотерма кризистік деп аталады. Кризистік ҒКН изотерма, изотерманың иілу нүктесі болып та-былатын бір ғана К нүктеден баска жерлерде монотонды төмен түседі. Ол нүктеде изотермаға жанама горизонтал болып табылады. К нүкте кризистік
деп аталады. Оғансәйкес келетін р к қысым, У к көлем және Т к температу-ралар да кризистік деп аталады. Осы күйдегі затты (қысымы, көлемі жөне температурасы кризистік күйдегі) кризистік куйде түр дейді.
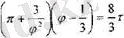
р к , У к , Т к кризистік параметрлерді табу үшін кризистікнүктеде(4. 8) тең-деудің
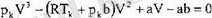
теңдеуге өтетіндігін пайдаланамыз. Бүл жерде барлық үш түбір де бірдей және Ү к болатындықтан, теңдеуді
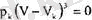
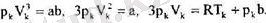
Оларды шешсек, онда:
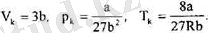
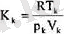
қатынасы кризистік коэффициент деп аталады. Ван-дер-Ва-
альс теңдеуі бойынша кризистік коэффициент
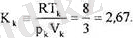
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz