Екінші ретті дискретті цифрлық сүзгілер: z-жазықтықтағы нөлдер мен полюстер, импульстік жауап және амплитуда-жиіліктік сипаттаманы талдау


КОММЕРЦИЯЛЫҚ ЕМЕС АКЦИОНЕРЛІК ҚОҒАМ
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Аэрокосмостық және ақпараттық технологиялар факультеті
«Электроника» кафедрасы
«Сигналдарды цифрлық өңдеудің негіздері» пәні бойынша
Курстық жұмыс
Орындаған: ПСк тобының
Студенті:
Нұсқа:78
Тексерген: аға оқытушы
Бакирова Н. С.
Алматы 2014
Кіріспе
Курстық жұмыстың негізгі мақсаты сызықты дискретті жүйені математикалық суреттеу сияқты, екінші ретті ШИС-сүзгілер мен СИС-сүзгілердің параметрлерін бағалаумен білімді нығайту және толықтыру болып табылады.
№1 және №2 есептеу-сызба жұмыстары беріліс функциясы түрінде көрсетілген екінші ретті ШИС-сүзгінің уақыттық пен жиілік талдауымен, z -жазықтығының талдауымен, ал №3 есептеу-сызба жұмысы берілген кіріс сипаттамалары бойынша рекурсивті емес сүзгінің шығыс параметрлерінің бағалауымен байланысты.
№1 тапсырма
Цифрлық сүзгі беріліс функциясының көпмүшелері
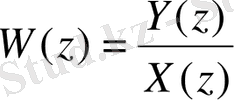 студенттің сынақ кітапшасы нөмірінің соңғысының алдындағы (N
соңғ. алд.
) және соңғы (N
соңғы
) цифрларына байланысты 1 кестенің берілген нұсқасына қарай таңдалады.
студенттің сынақ кітапшасы нөмірінің соңғысының алдындағы (N
соңғ. алд.
) және соңғы (N
соңғы
) цифрларына байланысты 1 кестенің берілген нұсқасына қарай таңдалады.
1 кестеде берілген бойынша 2-ретті нормаланбаған ШИС-сүзгісінің
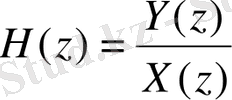 беріліс функциясының келесі тапсырмаларын орындау қажет.
беріліс функциясының келесі тапсырмаларын орындау қажет.
1. 1 Нөлдер және полюстер картасын салу.
1. 2 Сүзгінің орнықтылығын бағалау.
1. 3 Импульстік сипаттаманың формуласын жазу және сол бойынша импульстік сипаттаманың 5 санауын есептеу.
1. 4 Импульстік сипаттаманың графигін салу (5 санау) .
1 кесте
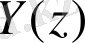
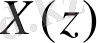
Беріліс функциясы тапсырмасының мысалын келесі көпмүшеліктер түрінде қарастырамыз:
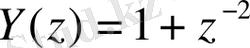 ;
;
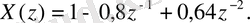
Онда
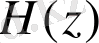 келесі түрде болады:
келесі түрде болады:
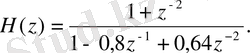
Нөлдер мен полюстер картасын саламыз, ол үшін беріліс функциясын теріс дәрежесіз түрге түрлендіреміз
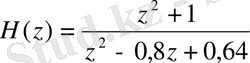 .
.
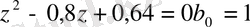
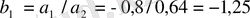
Д<0
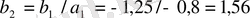
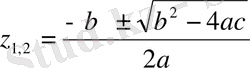
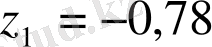
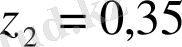
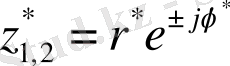 ,
,
мұндағы
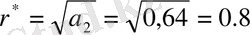 ,
,
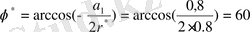
Нөлдер мен полюстер картасы 1 суретте көрсетілгендей түрде болады.
Im
+1 Re
-1 1
1 сурет
Импульстік сипаттаманың есебі келесі формула бойынша шығарылады:
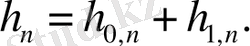
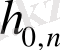 құраушы импульстік сипаттаманың бес нүктесі бойынша есеп жүргіземіз:
құраушы импульстік сипаттаманың бес нүктесі бойынша есеп жүргіземіз:
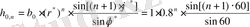 ;
;
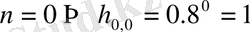 ;
;
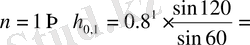 ;
;
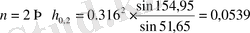 ;
;
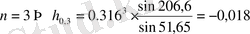 ;
;
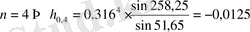 .
.
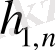 құраушы импульстік сипаттаманың бес нүктесі бойынша есеп жүргіземіз:
құраушы импульстік сипаттаманың бес нүктесі бойынша есеп жүргіземіз:
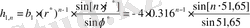 ;
;
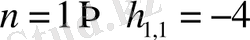 ;
;
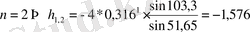 ;
;
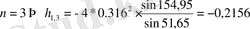 ;
;
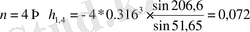 .
.
Импульстік сипаттаманың бес жүргізілген санаудың есебін 2 кестеге енгіземіз.
2 кесте
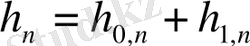
Импульстік сипаттаманың графигі 2 суретте көрсетілген.
№2 тапсырма
1 кестеде берілген бойынша 2-ретті нормаланбаған ШИС-сүзгісінің
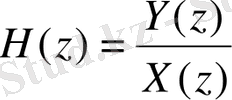 беріліс функциясының келесі тапсырмаларын орындау қажет:
беріліс функциясының келесі тапсырмаларын орындау қажет:
1) экспресс-талдау формулалары бойынша АЖС максимумына шамалас орналасқан
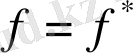 және нөлге, 0, 25-ке, 0, 5-ке тең нормаланған жиіліктерде амплитудалы-жиіліктік сипаттаманы (АЖС) есептеу;
және нөлге, 0, 25-ке, 0, 5-ке тең нормаланған жиіліктерде амплитудалы-жиіліктік сипаттаманы (АЖС) есептеу;
2) АЖС формуласын жазу және оның максимумын анықтау;
3) кешенді-түйістірілген нөлдердің болуы кезінде минимумы немесе нөлі шамалас келетін АЖС нүктесін анықтау, яғни
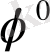 бұрышына сәйкесті
бұрышына сәйкесті
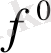 нормаланған жиілікті анықтау;
нормаланған жиілікті анықтау;
4)
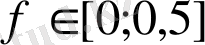 нормаланған жиілік аралығында нормаланбаған сүзгінің АЖС графигін тұрғызу және сүзгінің іріктелуін анықтау;
нормаланған жиілік аралығында нормаланбаған сүзгінің АЖС графигін тұрғызу және сүзгінің іріктелуін анықтау;
5) сүзгінің нормалануын орындау;
6)
 нормаланған жиілік интервалында нормаланған сүзгінің АЖС графигін тұрғызу.
нормаланған жиілік интервалында нормаланған сүзгінің АЖС графигін тұрғызу.
Айғақты коэффициенттері бар сүзгінің жиіліктік сипаттамасын толық суреттеу үшін оны
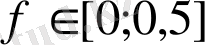 нормаланған жиіліктің негізгі жолағында беру жеткілікті.
нормаланған жиіліктің негізгі жолағында беру жеткілікті.
Екінші ретті буынның АЖС-ын бағалауға
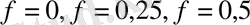 үшін экспресс-талдау формулаларын пайдалануға болады, ол мына түрде болады
үшін экспресс-талдау формулаларын пайдалануға болады, ол мына түрде болады
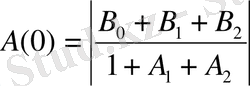 ;
;
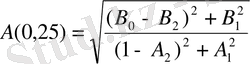 ;
;

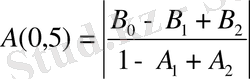 .
.
АЖС максимумы
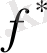 нормаланған жиілікке шамалас орналасады, ол
z
- жазықтығындағы полюс жағдайындағы
нормаланған жиілікке шамалас орналасады, ол
z
- жазықтығындағы полюс жағдайындағы
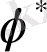 бұрышына сәйкес келеді
бұрышына сәйкес келеді
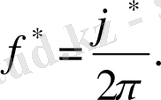
Амплитудалы-жиіліктік сипаттаманың формуласын жазамыз және ол бойынша
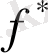 жиілігінде АЖС максимумын анықтаймыз.
жиілігінде АЖС максимумын анықтаймыз.
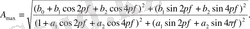
2 кесте
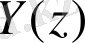
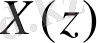
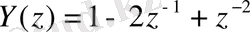 ;
;
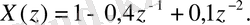
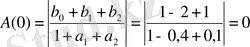 ;
;
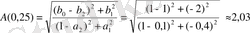 ;
;
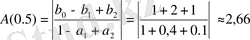 .
.
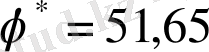
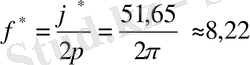
Бұл максимумның есебін мына формула бойынша шығарамыз:
 .
.
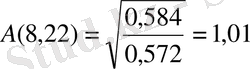
Төрт есептеу нүктелері бойынша тұрғызылған АЖС графигі 3 суретте көрсетілген.
Нормаланған көбейткіш мына формула бойынша анықталады:
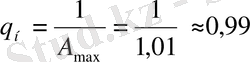 .
.
Онда нормаланған сүзгінің беріліс функциясы мынаған тең
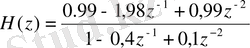 .
.
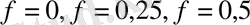 нормаланған жиіліктерде нормаланған сүзгінің АЖС-ң үш мәнінің есебін шығарамыз:
нормаланған жиіліктерде нормаланған сүзгінің АЖС-ң үш мәнінің есебін шығарамыз:
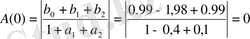 ;
;
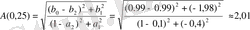 ;
;
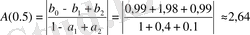 ;
;

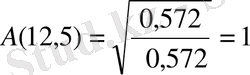
4 суретте
 [0, 1] жиілік диапазонында тұрғызылған нормаланған сүзгінің АЖС-ң графигі көрсетілген.
[0, 1] жиілік диапазонында тұрғызылған нормаланған сүзгінің АЖС-ң графигі көрсетілген.
№3 есептеу-сызба жұмысы
3 кесте бойынша, сынақ кітапшасы нөмірінің соңғы цифрымен анықталатын берілген нұсқаға сәйкес, { x( n ) } кіріс дискретті тізбектілігінің санауы мен { h(m) } импульсті сипаттаманың сәйкесті санауын анықтау керек, осылар бойынша келесі әрекеттерді орындау қажет:
1) кіріс дискретті тізбектіліктің Z - түрленуін есептеу;
2) берілген импульсті сипаттама бойынша дискретті бұрауды анықтау және есептелген {y(n) } шығыс санауларының графигін тұрғызу;
3) H(z) беріліс функциясын анықтау және рекурсивті емес сүзгінің сұлбасын тұрғызу.
3 кесте
{x(n) } кіріс дискретті тізбектіліктің тура Z-түрленуін мына формула бойынша алуға болады
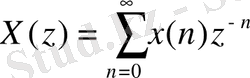 .
.
Мысалы, егер {x(n) } = {1, 1, 0} берілсе, онда
 .
.
Дискретті тізбектің шығысындағы сигнал тізбектің кірісіндегі сигналмен байланысты екені дискретті бұрау формуласымен белгілі, сондықтан дискретті шығыс тізбектіліктің n-ші санауы мына формуламен анықталады:
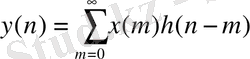 ,
,
мұндағы h(n-m) - дискретизацияның m периодқа қалып тұрған импульсті сипаттамасы.
Сызықты дискретті жүйенің реакциясын нөлдік бастапқы шарттар кезінде {y(n) } бұрау формуласы бойынша есептеу үшін оның әсері тіркелген, ал солдан оңға қарай жылжымалысы - төменде көрсетілгендей импульстік сипаттама болып келеді:
- n=0,
h(0-m),
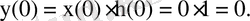
- n=1
h(1-m)
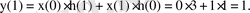
- n=2
h(2-m)

- n=3
h(3-m)

- n=4
h(4-m)

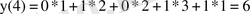
- n=5
h(5-m)
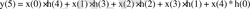
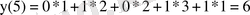
- n=6
h(6-m)

- n=7
h(7-m)
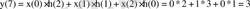
- n=8
h(8-m)
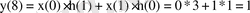
- n=9
h(9-m)
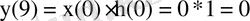
H(z) дискретті тізбектің беріліс функциясы былай анықталады
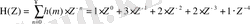 .
.
Қорытынды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz