Кванттық теорияның басты тұжырымдарын тәжірибе жүзінде негіздеу.Франк және Герц тәжірибелері

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министрлігі

Семей қаласының Шәкәрім атындағы Мемлекеттік университеті

АГРАРЛЫҚ ФАКУЛЬТЕТ

Физика пәнінен

СӨЖ

Тақырыбы: Кванттық теорияның басты тұжырымдарын тәжірибе жүзінде негіздеу. Франк және Герц тәжірибелері.

Орындаған: ғылыми биология мамандығының

2 курс студенті Еркінов. М. Е.

БЛ-409

Тексерген: Рахимбердина. А. Т.

Семей қаласы, 2015 жыл

Жоспар

Кванттық теорияның басты тұжырымдарын тәжірибе жүзінде негіздеу:

Атомдық спектрлер. Сериялық заңдылықтар
Спектрлiк терм. Комбинациялық принцип
Бор постулаттары.
Сутегi атомының энергия деңгейлерi және спектрi
Сутегi атомын модельдiк (Бор моделi тұрғысынан) қарастыру.
Франк-Герц тәжірибелері
Қорытынды
Пайдаланылған әдебиеттер

Атомдық спектрлер. Сериялық заңдылықтар.

19-ғ. екiншi жартысында жүргізiлген зерттеулер нәтижесiнде әрбiр химиялық элементтiң атомдарының буы белгiлi бiр қолайлы жағдай жасалып қоздырылғанда сызықтық спектр деп аталатын жеке сызықтар жиынтығынан тұратын сызықтық спектр шығаратындығы; және де әрбiр химиялық элемент атомдарына тек осы элементке тән нақты сызықтық спектр сәйкес келетiндiгi тағайындалды.

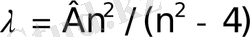Сутегiнiң сызықтық спектрiн егжей-тегжейлi зерттеп, швейцариялық мектеп мұғалiмi И. Бальмер (1885) спектрде сол кезде белгiлi тоғыз сызықтың толқын ұзындықтарын мына формула бойынша

табуға болатындығын тапты; мұндағы В=364, 6 нм, ал n=3, 4, 5, . . . бүтін мәндерiн қабылдайды.

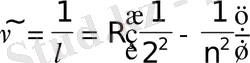Соңғы формуланы Швед ғалымы И. Ридберг (1890) басқа түрде жазуды ұсынды:

мұндағы -спектрлiк сызықтың толқындық саны, см-1, -толқын ұзындығы, R-тұрақты шама, Ридберг тұрақтысы деп аталады; n=3, 4, 5, . . . формула өте жоғары дәлдiкпен тәжiрибеге сәйкес келетiн нәтижелер бередi.

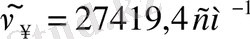
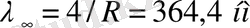Ридберг тағайындаған формула қамтитын сутегi атомының спектрлiк сызықтар тобы Бальмер сериясы деп аталады. Осы формулаға қарағанда n-нiң мәнi ұлғайған сайын көршiлес сызықтардың толқын ұзындық айырмасы кеми бередi, спектрлiк сызықтар арасы жақындай түседi. Ең соңында, n болғанда Бальмер сериясының шекарасы

немесе пайда болады.

Сутегi атомы спектрiнде Бальмер сериясынан басқа сызықтар да бар.

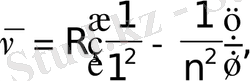Спектрдiң ультракүлгін бөлiгiндегi бiр топ сызықтар Лайман (1906) сериясы деп аталады:

n=2, 3, 4, . . .

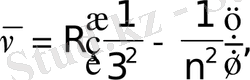Сутегi спектрiнiң жақын инфрақызыл бөлiгiнде Пашен (1908) сериясы деп аталатын бiр топ сызық бар.

n=4, 5, 6, . . .

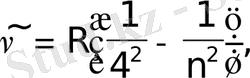Бұдан басқа спектрдiң алыс инфрақызыл бөлiгiнде үш серия бар.

Брэкет сериясы (1922) : n=5, 6, 7, . . .

П фунд сериясы (1924) : n=6, 7, 8, . . .

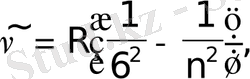Хэмфри сериясы (1953) : n=7, 8, 9, . . .

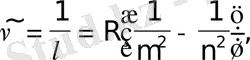Сонымен, сутегi атомының барлық спектрлiк сызықтарын мынадай жалпы формуламен өрнектеуге болады:

мұндағы m және n-бүтін сандар, және m<n; берiлген серия үшін n= m+1, m+2, . . . болады. Лайман сериясы үшін m=1, Бальмер сериясы үшін m=2 және т. т.

Спектрлiк терм. Комбинациялық принцип

Классикалық физика заңдарына құрылған планетаарлық жүйе болып табылатын және $\mathrm{\Delta}$ бөлшектерінің шашырауы бойынша жүргізілген тәжірибелердің нәтижелерін талдауға негізделген Резерфордтың атомдық моделі тәжірбиелік фактілермен толық қарама-қарсы қайшылықта болды. Біріншіден, классикалық теорияға сәйкес, электрон ядроның айналасында дөңгелектік орбита бойынша қозғала отырып, үздіксіз сәуле шығаруға тиіс. Шындығында, атом тек кейбір шарттар негізінде ғана сәуле шығарады. Екіншіден, Резерфордтың атомдық моделі тұрақсыз болды, бірақ шындығында атом тұрақты жүйе болып табылады. Үшіншіден, Резерфорд моделіндегі атомның сәуле шығару спектрі үздіксіз (тұтас) болуы керек еді, ал бірақ тәжірибеде атомның сәуле шығаруы сызықтық спектр болып табылады. Бұл деген сөз, классикалық физика заңдарын атом теориясына біркелкі қолдану тәжірибелік фактілермен қарама-қарсы қайшылықта болуға әкелді.

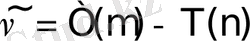Атомдардың сызықтық спектрлерiн зерттеу нәтижелерiне сүйенiп, Ридберг (1889) берiлген серияның барлық сызықтарының толқындық сандары (жиiлiктерi) мына қатынасты

қанағаттандырады деген қорытынды жасады; мұндағы m-тұрақты, серияны анықтайтын тұрақты мәнге ие сан, ал n cанының өзгерiсi (n=m+1, m+2, . . . ) берiлген серияның барлық сызықтарын бередi;

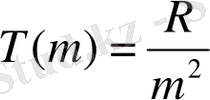Сутегi атомының сериялық формуласымен салыстырудан спектрлiк термдердiң тиiсiнше мына қатынастарға

және тең болатындығы келiп шығады.

Бор постулаттары.

Аталған қарама-қайшылықтарды шешу үшін жаңа түсінiктер қажет болды. Н. Бор (1913) алғаш болып атомның планетарлық моделiн ендi ғана жаңадан пайда бола бастаған кванттық теориямен (Планк гипотезасы) байланыстыру керектiгiн алғашқы болып түсіндi.

Бор теориясының негiзiне екi постулат алынған.

1-постулат (стационарлық күйлер постулаты) : атомды нақты дискреттiк энергия мәндерiмен сипатталатын стационарлық уақытқа байланысты өзгермейтiн күйлер болады, бұл күйлерде ол энергия шығармайды. Атомның стационарлық күйлерiне стационарлық орбиталар сәйкес келедi; осы орбиталар бойынша электрондар қозғалады. Электрондар стационарлық орбиталар бойымен қозғалғанда электромагниттiк толқындар шығармайды.

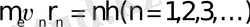Атомның стационарлық күйiндегi дөңгелек орбита бойынша қозғалатын электронның импульс моментi шартын қанағаттандыратын дискреттi квантталған мәндер қабылдауы тиiс; мұндағы me-электрон массасы, n-радиусы rn n-i орбитадағы оның жылдамдығы; =h/2.

2-постулат (жиiлiктер ережесi) : атом бiр стационарлық күйден басқасына ауысқан жағдайда энергиясы тиiстi стационарлық күйлер энергияларының айырымына фотон шығарылады (жұтылады) .

E _m < E _n болған жағдайда фотон шығарылады, E _m > E _n болғанда фотон жұтылады. Мүмкін болатын кванттық ауысуларға сәйкес келетiн дискреттiк v = (E _n - E _m ) /h жиiлiктер жиыны атомның сызықтық спектрiн анықтайды.

Бiрiншi постулат орнықты атомның болатындығын растайды. Ал екiншi постулат тiкелей комбинациялық принциппен байланысқан.

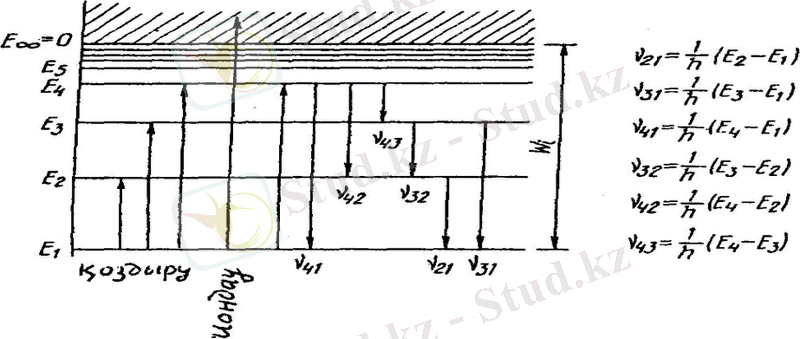Бор постулаттарына сүйенiп комбинациялық принциптi көрнекi түрде көрс ететiн диаграммасын тұрғызуға болады

Сутегi атомының энергия деңгейлерi және спектрi

Сутегi атомының энергетикалық спектрi мына формуламен анықталады:

мұндағы A=hcR энергетикалық тұрақты; 1, 2, 3, . . .  мәндерiн қабылдайтын n саны бас кванттық сан деп аталады. Ол сутегi атомының энергия деңгейлерiн анықтайды. Энергияның терiс таңбалы болуы атомдағы электронның байланысқан күйде тұрғандығын көрсететiндiгi жайында айтылған болатын.

Сутегi атомын модельдiк (Бор моделi тұрғысынан) қарастыру.

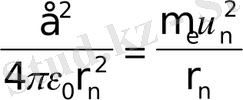Сутегi атомындағы электронның қозғалысын қарастырайық; Кулондық күш әсерiнен шеңбер бойымен қозғалатын электрон үшін Ньютонның 2-заңы негiзiнде мына теңдiктi жазамыз

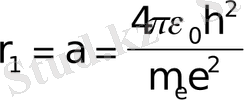
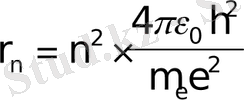Осы теңдiкке квантталу шартынан n жылдамдықты қойып, теңдiктi rn-ге қатысты шешемiз; сонда n-i стационарлық орбита радиусы үшін өрнек алынады: (n=1, 2, 3, . . . )

Ядроға ең жақын орбитаға n=1 сәйкес келедi;

Бұл тұрақты шама Бор радиусы деп аталады және ол сутегi атомының ең кiшi орбитасының мөлшерiн анықтайды.

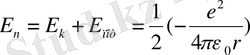Сутегi атомындағы электронның толық энергиясы оның кинетикалық энергиясы мен ядроның электростатикалық өрiсiндегi потенциалдық энергиясының қосындысына тең:

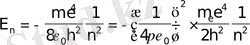Стационарлық орбиталар радиустары үшін квантталған мәндерiн ескергенде

мұндағы минус таңбасы электрон байланысқан күйде тұрғандығын бiлдiредi. Осы өрнектен сутегi атомындағы электрон энергиясы тек дискреттi мәндер қабылдайтындығы, яғни атом энергиясының квантталғандығы келiп шығады.

Франк-Герц тәжірибесі

Атомдардағы стационарлық күйлердің (дискретті энергетикалық деңгейлердің) пайда болуы туралы Бор постулаттары және жиіліктердің ережесі 1913 жылы Д. Франк пен Г. Герцтің тәжірибелерінде өзінің орнын тапты.

Өте қатты қызған спираль түріндегі К катоды электрондарды шығарады, электрондар электр өрісінің әсерінен гальванометрге жалғанған А анодқа қарай қозғалады. Катод пен анодтың арасында S тор электроды бар. Бұл барлық жүйе ішінен ауасы сорылып алынған шыны баллонына орналастырылады. Баллонда, шамамен 15 Па дейінгі қысымда сынап булары енгізілген. Катод пен тор арасында потенциалдар айырымы U1 болатын үдеткіш электр өрісі жасалған, ал тор мен анод арасында потенциалдар айырымы U2 болатын шамасы 0, 5 В-тан аспайтын әлсіз тежеуші кернеу өрісі жасалған. Электрондар сынап атомдарымен екі жақты әсерлеседі. Соқтығысудың бірінші түрі серпімді соққылар, олар электрондардың жылдамдығын өзгерусіз қарапайым шашырауға әкеледі. Мұндай серпімді соққылар тізбектегі толық токтың болмауының себебі бола алмайды, ол үдеткіш U1 потенциалдар айырымы артуына байланысты өседі. Соққының екінші түрі - электрондардың сынап атомдарымен серпімсіз соққысы - электрондардың энергия жоғалтуына байланысты және ол бұл энергияларды сынап атомдарына беруіне байланысты. Бірақ, Бор постулаттарына сәйкес, сынап атомы кез-келген энергияны қабылдамауы мүмкін, ол тек әртүрлі энергетикалық деңгейлердегі энергиялар айырымына тең энергияның белгілі үлесін ғана қабылдайды. Сынап атомының негізгі күйіне жақын күй - қозған күй болып табылады, ол негізгі күйден 4, 86 эВ энергия айырымына өзгереді.

Осымен байланысты өрістің үдететін электрондары энергия айырымы еU14, 86 эВ-қа дейін жеткенше тек серпімді соққыларға ие болады. Электрондар энергиясы 4, 86 эВ жетісімен серпімсіз соққылар басталады, бұл кезде электрон толық энергияны сынап атомына береді. Сынап атомымен соқтығысу нәтижесінде өзінің энергиясын жоғалтқан электрон тор мен анод арасындағы тежеуші өрісті жеңе алмай, нәтижесінде электрон анодқа жете алмайды. Бұл анод тогының кенет тез түсуіне әкеледі.

Осындай құбылыс еU124, 86 эВ кезінде де болады, жалпы айтқанда еU1n4, 86 эВ кезінде де болатындығын Бор постулаттары дәлелдейді.

Бор теориясы атомдық физикасының дамуы барысында өте зор орын алады. Ол сутегі атомы энергиясының сәулеленуі мен жұтылуының сызықтық спектрлерін түсіндіруге, теориялық түрде сутегі типтес жүйелер үшін Ридберг тұрақтысын есептеуге, атомның тұрақтылығын, рентгенттік сәулеленудің табиғатын және тағы басқа құбылыстарды түсіндіруге мүмкіндік берді. Бірақ Бор атомының моделі атомдағы электрондардың қозғалысы туралы жартылай классикалық көзқарасқа байланысты өз ішінде қайшылықтар болды. Бор теориясы ядродан басқа екі электроннан құралған гелий атомының моделін жасай алмады. Сонымен бірге, Бор теориясы спектралды сызықтардың интенсивтігіндегі әртүрлілікті түсіндіре алмады. Оларды есептеу үшін Бор тағайындаған сәйкестік принципін қолдануға тура келді. Бұл принцип бойынша кванттық механиканың нәтижелері үлкен кванттық сандар кезіндегі классикалық нәтижелерге сәйкес болуы керек. Бұл принцип, классикалық теорияның дамуы болып табылатын кез-келген теория мен алғашқы классикалық теория арасында заңды байланыс болатынын, яғни жаңа теория ескі теорияға шекті жағдайларда ауысатындығын көрсетеді.

Қорытынды

Сонымен, қорыта келгенде, сызықтық спектр әрбір химиялық элементтiң атомдарының буы белгiлi бiр қолайлы жағдай жасалып қоздырылғанда шығады және ол жеке сызықтар жиынтығынан тұрады . 19 ғасырдың ІІ жартысындағы зерттеулер нәтижесінде әрбiр химиялық элемент атомдарына тек осы элементке тән нақты сызықтық спектр болатындығы анықталған. Сутегiнiң сызықтық спектрiн 1885 жылы егжей-тегжейлi швейцариялық мектеп мұғалiмi И. Бальмер зерттеген болатын. Ол сол кезде спектрде белгілі тоғыз сызықтың толқын ұзындығын анықтауға болатындығын көрсетті. Ал Ридберг тағайындаған формула қамтитын сутегi атомының спектрлiк сызықтар тобы Бальмер сериясы деп аталады. Бұл серия бойынша нақты сандардың мәнi ұлғайған сайын көршiлес сызықтардың толқын ұзындық айырмасы кеми бередi, спектрлiк сызықтар арасы жақындай түседi және ең соңында оның шекарасы пайда болады. Осы сериядан басқа сутегi атомы спектрiнде: ультракүлгін бөлiгiндегi бiр топ сызықтар Лайман сериясы, ал жақын инфрақызыл бөлiгiнде Пашен сериясы, және бұлардан басқа спектрдiң алыс инфрақызыл бөлiгiнде Брэкет сериясы, П фунд сериясы, Хэмфри сериясы деп аталатын үш сериясы бар.

1911 ж. Резерфорд атомның ядролық (планетарлық) моделiн (үлгiсiн) ұсынды; бұл атом құрылысы жөнiндегi қазiргi көрiнiстерге келудегi маңызды қадам болды. Осы модельге сәйкес Ze оң заряды бар ядроны дөңгелек (немесе эллипстiк) орбита бойынша электрондар электростатикалық тартылыс күшi әсерiнен айналып жүредi (гравитациялық тартылыс күштерi әсерiнен планеталардың Күндi айналатындығына ұқсас) . Ядро заряды электрондардың қосынды зарядына тең, өйткенi атомдар электрлiк бейтарап жүйе. Резерфорд моделi, алайда, классикалық физика шеңберiнде орнықсыз болады. Классикалық электродинамика заңдарына сәйкес ядроны айнала қозғалатын электрон электромагниттiк толқындарды үздіксiз шығаруға, сондықтан да ол өз энергиясын жоғалта беруге тиiс. Осының нәтижесiнде электрондар ядроға бiрте-бiрте спираль бойымен жақындап, соңында ядроға құлайды. Осы қорытындылар атомдардың бақыланатын орнықтылығына қарама-қайшы келедi. Осы қарама-қайшылықтарды шешу үшін Н. Бор 1913 жылы өзінің әйгілі постулаттарын ұсынды. Оның ұсынған посулаттарына келетін болсақ, бірінші посулатында, атомда электрондар қозғалатын стационар орбиталар бар. Стационар орбитадағы атомдар сәуле шығармайды десе, екінші посулатында, электрон энергиясы Е _n стационар орбитадан энергиясы Е _m стационар орбитаға ауысқанда, энергия кванты түрде жұтылады не шығарылады деген тұжырымдар жасады. Н. Бордың бiрiншi постулаты орнықты атомның болатындығын растайды. Ал екiншi постулаты тiкелей комбинациялық принциппен байланысқан. Н. Бордың кванттық теориясын дәлелдеуде Франк - Герц тәжірибелері маңызды рөл атқарды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.