Дөңгелек қуыстың маңайындағы серпімдіпластикалық ағысын есептеу

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

Әл-Фараби атындағы Қазақ Ұлттық Университеті

Механика-математика факультеті

Механика кафедрасы

«Қорғауға жіберілді» «»

Кафедра меңгерушісі

ф. -м. ғ. д., профессор Қалтаев А. Ж

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: « ДӨҢГЕЛЕК ҚУЫСТЫҢ МАҢАЙЫНДАҒЫ СЕРПІМДІПЛАСТИКАЛЫҚ АҒЫСЫН ЕСЕПТЕУ »

мамандық 050603 - «Механика»

Орындаған Нургалиева А. Е.

Ғылыми жетекші Ысқақбаев Ә. Ы.

ф. -м. ғ. д., профессор

Норма бақылаушы Туралина Д. Е.

ф. -м. ғ. к., доцент

Алматы, 2013 ж.

Реферат

Жұмыстың көлемі: жұмыс 20 беттен, 1 графиктен, 4 суреттен тұрады.

Зерттеу объектісі: дөңгелек қуысы бар пластинаның серпімдіпластикалық күйін зерттеу.

Жұмыстың мақсаты : дөңгелек қуысы бар пластинаның көтеру қабілеттілігін ыдырату әдісі бойынша зерттеу. Қуыстың маңайындағы кернеуленген күйді сипаттайтын анықтауыш теңдеулерді есептеу.

Зерттеу әдісі: Марle қолданбалы программа арқылы есептің графикалық кескінің шығару.

Мазмұны

I. КІРІСПЕ . . . . . . 5

II. Есептің қойылымы . . . 6

1. 1-есеп. Дөңгелек қуысы бар пластинаның серпімді күйін талдaу.

1. 1 Дөңгелек қуысты жазықтықты жан-жақты бірқалыпты созу . . . 7

1. 2 Эридің кернеулер функциясы . . . 8

1. 3 Mизес шарты . . . 9

1. 4 Cерпімдіпластикалық теңдеулерді ыдырату (Кукуджановтың əдісі) . . . 11, 12, 13

2. 2-есеп. Серпімді аймақта шекаралық есепті талдау . . . 14

3. 3-есеп . Уилкинс-кукуджанов ыдырату әдісі бойынша кернеу девиаторының компаненттерін табу . . . 15

3. 1. Сығылмайтын идеал пластикалық дененің көтеру қабілеттілігі [6] . . . 16

3. 2. Пластикалық ағу теориясы . . . 17

4. 4 -есеп. Пластикалық аймақта шекаралық есепті шығару . . . 18

4. 1. Жазық деформация . . . 19

5. Жазық деформация кезіндегі қуыс маңайындағы пластикалық кернеуленген күйді қарастырамыз. . . . 20, 21

III. қОСЫМША

III. ҚОРЫТЫНДЫ…… . . . . . . 22

Пайдаланылған әдебиеттер тізімі … . . . . . . … . . . 23

Шартты белгілер:

$\sigma_{ij}^{e}$ - серпімді аймақтағы кернеу тензорларының құраушылары;

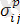$\sigma_{ij}^{p}$ - пластикалық аймақтағы кернеу тензорларының құраушылары;

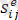
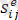- серпімді аймақтағы кернеу девиаторының құраушылары;

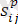
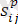- пластикалық аймақтағы кернеу девиаторының құраушылары;

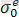$\sigma_{0}^{e}$ - серпімді аймақтағы орташа нормаль кернеу;

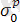
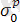- пластикалық аймақтағы орташа нормаль кернеу;

$r, \theta, z -$ цилиндрлік координаттар;

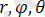$r, \varphi, \theta$ - сфералық координаттар;

$\tau_{i}^{e}$ -серпімді аймақтағы жанама кернеулердің жиілігі;

$\sigma_{T}$ - созылу кезіндегі аққыштық шегі;

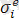$\sigma_{i}^{e}$ -серпімді аймақтағы кернеу жиілігі;

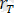$r_{T}$ - серпімді және пластикалық аймақты бөлетін шекаралық радиус;

а - внутренний радиус полого шара

b - наружный радиус полого шара

I. КІРІСПЕ

Пластикалық ағу теориясының негізгі болжамдары:1. Деформацияның жылдамдығы. [1]
$\ \ \ \ \ \ \ \ \ \ \ \ \ \dot{\varepsilon_{ij}} = {\dot{\varepsilon}}_{ij}^{e} + {\dot{\varepsilon}}_{ij}^{p}$ , (1. 1)

мұндағы ${\dot{\varepsilon}}_{ij}^{e}$ - серпімді деформацияның жылдамдығы, ${\dot{\varepsilon}}_{ij}^{p} -$ пластикалық деформацияның жылдамдығы.

2. Пластикалық шарт:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ F\lbrack I_{i}(\widehat{\sigma}$ ), $I_{i}(\widehat{\varepsilon}$ , ${), I}_{i}\left( \widehat{\dot{\varepsilon}} \right), L_{K}\rbrack = 0,$ (1. 2)

(i=1, 2, 3; k=1, 2, . . n)

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (I}_{i}(\widehat{\sigma}$ ) - кернеу тензорының инварианттары, $I_{i}(\widehat{\varepsilon}$ ) - деформация тензорының инварианттары, $I_{i}\left( \widehat{\dot{\varepsilon}} \right) -$ деформация жылдамдығы тензорының инварианттары, $L_{K} - ортаның$ ішкі параметрлері.

3. Байланыстырылған ағу заңы.

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ έ_{ij}^{p} = \dot{\Lambda}\frac{\partial F}{\partial\sigma_{ij}}$ (1. 3)

F - аққыштық бет теңдеуі. (1. 3)

4. Ортаның ішкі параметрлерін анықтау үшін эволюциялық параметрлер

${\dot{\ L}}_{k} = f_{k}\lbrack I_{i\ }\left( \widehat{\sigma} \right), L_{k}$ ] . (1. 4)

[5] -ші жұмыста серпімдіпластикалық ағыстарды есептеудің жаңа тәсілін қарастырып, есепті төртке бөлген:

1-ші есеп. Материал серпімді болсын деп серпімді сызықты табу үшін, шекаралық есепті шығарамыз. Мизес пластикалық критерийін пайдаланып, пластикалық аймақты табамыз.

2-ші есеп. Серпімді аймақ пен пластикалық аймақтың шекарасында Мизес пластикалық шарты орындалады деп, серпімді аймақта шекаралық есепті шығарамыз.

3-ші есеп. Кукуджанов ыдырату әдісін пайдаланып, пластикалық аймақта кернеу девиаторының компаненттерін табамыз.

4-ші есеп. Пластикалық аймақта Мизес шарты орындалады деп, шекаралық есепті шығарамыз.

II. ЕСЕПТІҢ ҚОЙЫЛЫМЫ

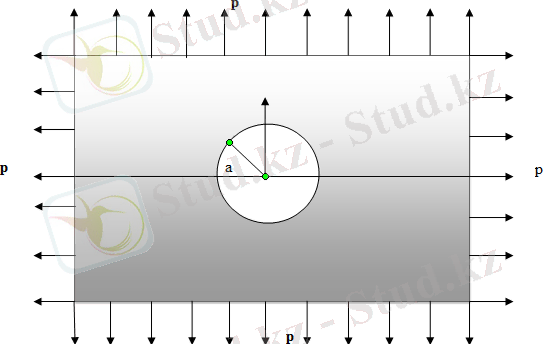
1 cурет-Дөңгелек қуысы бар пластина

[5 ] -ші әдісті пайдаланып, ыдырату әдісімен ''Дөңгелек қуыстың маңайындағы серпімдіпластикалық ағысын есептеу'' есебін талдаймыз.

1-ші есеп. Дөңгелек қуысы бар пластинаның серпімді күйін талдаймыз.

2-ші есеп. Серпімді аймақта шекаралық есепті талдау.

3-ші есеп. Пластикалық аймақта кернеу девиаторының компаненттерін анықтау.

4-ші есеп. Пластикалық аймақта шекаралық есепті талдау.

1. 1-ЕСЕП. ДӨҢГЕЛЕК ҚУЫСЫ БАР ПЛАСТИНАНЫҢ СЕРПІМДІ КҮЙІН ТАЛДAУ.

1. 1 Дөңгелек қуысты жазықтықты жан-жақты бірқалыпты созу [6]

Алдымен серпімді шектелмеген жазық пластинаны қарастырайық . [6] Оны шексіздікте берілген тұрақты кернеулермен p жан- жақты созатын болсақ, онда пластинада жалпыланған жазық кернеуленген күй жағдайы орын алады: декарттық координаталар жүйесінде (x, y, z)

$\sigma_{x} = \sigma_{y} = \sigma_{0}$ , $\tau_{xy} = 0, \ \sigma_{z}$ =0; ( 1. 11)

Цилиндрлік координаталар жүйесінде (r, θ, z)

$\sigma_{r}$ = $\sigma_{\theta}$ =p, $\tau_{r\theta} = 0, \sigma_{z} = 0.$ (1. 12)

Енді шектелмеген жазық пластинада радиусы а болатын қуыс пайда болсын деп есептеп оның пластинадағы кернеулердің өзгерісіне ықпалын зерттейміз.

Бұл есептің шектік шарттарын мына түрде жазамыз:

$\ \ \ {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{r}_{r = a} = 0;$

$\sigma_{r\ }_{r = \infty} = p,$ (1. 13)

мұндағы p-берілген тұрақты кернеу .

Эри функциясы Ф(r, θ) арқылы төмендегі түрде кіргізуге болады:

$\sigma_{\theta}$ = $\frac{\partial^{2}Ф}{\partial r^{2}}$

$\sigma_{r} = \frac{1}{r^{2}}\frac{\partial^{2}Ф}{\partial\theta^{2}} + \frac{1}{r}\frac{\partial Ф}{\partial r}\$

$\tau_{\tau\theta}$ = $\frac{\partial}{\partial r}$ ( $\frac{1}{r}\frac{\partial Ф}{\partial\theta})$ (1. 14)

${\ \nabla}^{2}\nabla^{2}$ Ф=0 (1. 15)

Эри функциясы Ф(r, θ) бигармоникалық теңдеуді (1. 15) қанағаттандыру керек, мұндағы Лаплас операторы

${\ \ \nabla}^{2}$ = $\frac{\partial^{2}}{\partial r^{2}} + \ \frac{1}{r}\frac{\partial}{\partial r}$ + $\frac{1}{r^{2}}\frac{\partial^{2}}{{\partial\theta}^{2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 16)

Қойылған есептің кернеуленген күйінің θ-бұрышына тәуелсіз екенін ескере отырып, бигармоникалық теңдеудің (1. 15; 1. 16) шешімін мына түрде жазамыз

$\ \ Ф(r) = Alnr + Br^{2}lnr + Cr^{2} + D$ (1. 17)

А, В, С, Dбелгісіз тұрақтылар.

Осы жалпы интегралды Эри формуласына (1. 15) қойып, кернеулерді табамыз.

${\ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{r}$ = $\frac{A}{r^{2}}$ +2Blnr+B+2C

${\ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{\theta} = - \frac{A}{r^{2}} + 2Blnr + 3B + 2C\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 18)

${\ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{Z}$ =0

Шекаралық шарттарды пайдаланып белгісіздерді табамыз.

A=- $pа^{2}$

2C=p

$B = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 19)

Қарастырылып отырған есептің кернеулері (1. 18) -ге (1. 19) -ді қойсақ мынандай формуланы аламыз.

$\ \ \ \ \ \ \ \ \ \ \ \left\{ \begin{array}{r} \sigma_{r} = p(1 - \frac{a^{2}}{r^{2}}) \\ \sigma_{\theta} = p(1 + \frac{a^{2}}{r^{2}}) \\ \sigma_{z} = 0 \end{array} \right. \ \ \ \$ p>0 (1. 20)

1. 2 ЭРИДІҢ КЕРНЕУЛЕР ФУНКЦИЯСЫ. [6]

Статикалық біртекті теңдеулерін ( $\frac{\partial\sigma_{x}}{\partial x} + \frac{\partial\tau_{xy}}{\partial y} + F_{x} = 0, \ \frac{\partial\tau_{xy}}{\partial x} + \frac{\partial\sigma_{y}}{\partial y} + F_{y} = 0$ ) ( 2. 42[6] ) қарастырайық:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\ \partial\sigma_{x}}{\partial x} + \frac{\partial\tau_{xy}}{\partial y} = 0, \frac{\partial\tau_{xy}}{\partial x} + \frac{\partial\sigma_{y}}{\partial y} = 0$ (1. 21)

Бұл жүйенің (1. 22) шешімін табу үшін, жаңадан Ф(x, y) функциясын - Эридің кернеулер функциясын, енгіземіз:

${\ \sigma}_{x} = \frac{\partial^{2}Ф}{\partial y^{2}}$ , $\sigma_{x} = \frac{\partial^{2}Ф}{\partial X^{2}}$ , $\tau_{xy} = - \frac{\partial^{2}Ф}{\partial x\partial y^{}}$ (1. 23)

Бұл шешім (1. 23) статиканың біртекті теңдеулерін (1. 22) қанағаттандырады.

Енді (1. 21) теңдеулер жүйесінің жалпы шешімін мына түрде жазуға болады:

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{x} = \sigma_{x}^{0} - \frac{\partial^{2}Ф}{\partial y^{2}}$ , $\sigma_{x} = \sigma_{y}^{0} - \frac{\partial^{2}Ф}{\partial X^{2}}$ , $\tau_{xy} = \frac{\partial^{2}Ф}{\partial x\partial y^{}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 24)

$\sigma_{z} = v\left( \sigma_{x}^{0} + \sigma_{y}^{0} \right) + v\nabla^{2}\ Ф,$

Мұндағы $\sigma_{x}^{0}, \ \sigma_{y}^{0}, \ \tau_{xy}^{0} - (1. 21) жүйенің\$ дербес шешімі, $\nabla^{2}(x, y) -$ Лаплас операторы.

1. 3 МИЗЕС ШАРТЫ [6]

Металдардың аққыштық күйін анықтайтын мизес шарты $\ \ {\ \ \ \ \ \ \ \ \sigma}_{i} = \sigma_{T}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 31)

мұндағы $\sigma_{i}$ - кернеулер қарқындылығы (1. 31), яғни Мизес алтыжақты призманы дөңгелек цилиндрмен алмастырған ( ә-Сурет [6] ) . Бұл цилиндрдің девиатор жазықтығындағы ізі - шеңбер ( б-Сурет [6] ), дұрыс алтыбұрышқасырттай сызылған шеңбер.

Қазіргі кезде бұл екі шарттар іс жүзінде бірдей пайдаланып кележатыр.

Енді Мизес шартын (1. 31) мына түрде жазуға болады.

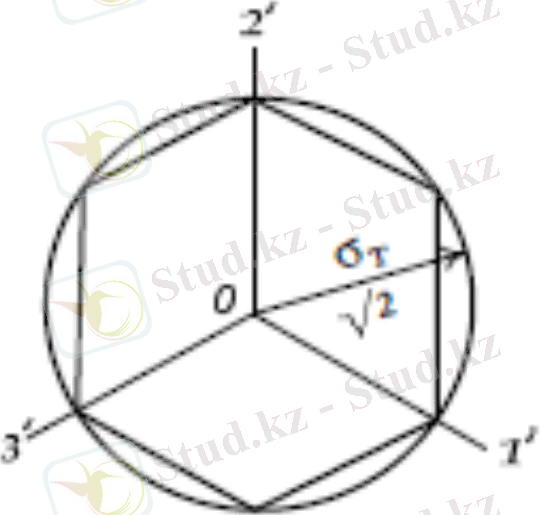
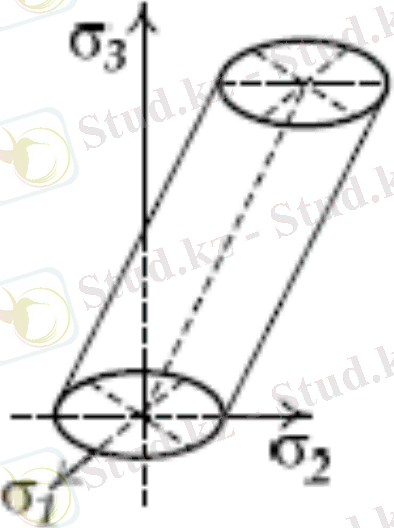
ә-сурет б-сурет

Қазіргі кезде бұл екі шарттар ісжүзіндебірдей пайдаланып келе жатыр. Енді Мизес шартын (1. 31) мына түрде жазуға болады . ${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \tau}_{i} = \tau_{T}$ (1. 32)

$\tau_{i} = \frac{1}{\sqrt{}6}\lbrack(\sigma_{r} - \sigma_{\theta}) ^{2} + (\sigma_{\theta} - \sigma_{z}) ^{2} + {(\sigma}_{z} - \sigma_{r}) ^{2}\rbrack^{\frac{1}{2}}$ (1. 33)

$\sigma_{T}$ =2 $\tau_{T}$ (1. 34)

мұндағы $\tau_{i}$ - жанама кернеулер қарқындылығы (1. 33), ал $\tau_{T}$ мен $\sigma_{T}$ арасындағы қатынас (1. 34) формуласымен анықталады.

$\sigma_{T} = 2\frac{1}{\sqrt{}6}\lbrack(\sigma_{r} - \sigma_{\theta}) ^{2} + (\sigma_{\theta} - \sigma_{z}) ^{2} + {(\sigma}_{z} - \sigma_{r}) ^{2}\rbrack^{\frac{1}{2}}$ (1. 35)

$\sigma_{T} = 2\frac{1}{\sqrt{}6}\lbrack(p(1 - \frac{a^{2}}{r^{2}}) - p(1 + \frac{a^{2}}{r^{2}}) ) ^{2} + (p(1 + \frac{a^{2}}{r^{2}}) ) ^{2} + ( - {p(1 - \frac{a^{2}}{r^{2}}) ) }^{2}\rbrack^{\frac{1}{2}}$ (А1)

(А1) -ден (20) шығады.

Мизестің пластикалық шартын (1. 31) және (A1) -ті пайдаланып, a=r болғанда

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p}_{T}$ = $\frac{1}{2}\sigma_{T}\mathbf{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ (1. 36)

табамыз.

Пластинканың жазық жалпыланған кернеуленген күйін келесі қатынаспен {I} -ді қолданып, анықталады:

$\sigma_{r} = p\left( 1 - \frac{a^{2}}{r^{2}} \right) ; \ \sigma_{\theta}$ =p(1+ $\frac{a^{2}}{r^{2}}) ; \sigma_{z} = 0,$ мұндағы p>0 (1. 37)

Пластикалық аймақ а радиусты дөңгелек қуыстың ішіне қарай таралады.

$p \geq p_{T}$ . $r_{T\ } \geq a\$

А= $\frac{r}{a}; \ \ \$ B= $\frac{\sigma_{r}}{p};$

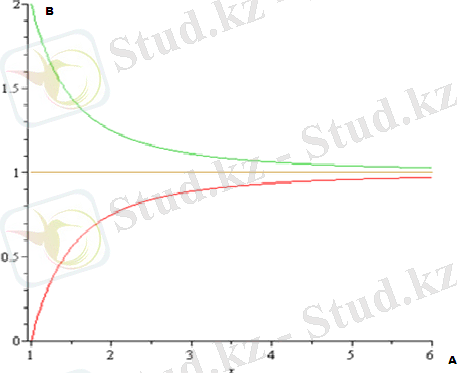
1 график- Пластинаның серпімді аймақтағы кернеуленген күйі (1. 37)

1. 4 . СЕРПІМДІПЛАСТИКАЛЫҚ ТЕҢДЕУЛЕРДІ ЫДЫРАТУ (КУКУДЖАНОВТЫҢ ƏДІСІ) [6]

Үлкен деформация кезінде орта үшін теңдеулер жүйесін Эйлер айнымалылары арқылы мына түрде жазуға болады (массаның, импульстің жəне энергияның сақталу заңдары) :

$\frac{\partial p}{\partial t} + \frac{\partial(\rho v_{k}) }{\partial x} = 0;$

$\frac{\partial(pv_{i}) }{\partial t} + \frac{\partial}{\partial x_{k}}\left( \rho v_{i}v_{k} \right) = \frac{\partial\sigma_{ik}}{\partial x_{k}};$

$\ \ \ \ \ \frac{\ \ \partial(\rho U) }{\partial t} + \frac{\partial(\rho v_{kU) }}{\partial X_{K}} = \frac{\partial(v_{i}\sigma_{ki) }}{\partial x_{k}} + \frac{\partial}{\partial x_{k}}\left( ж\frac{\partial T}{\partial X_{K}} \right) ;$ (1. 41)

Мұндағы ρ - тығыздық, $\overrightarrow{v}$ - жылдамдықвекторы, $\sigma_{ij}$ -кернеу тензорының кұраушылары, U - меншікті толық энергия, Т - температура, Ж - жылу өткізгіштік коэффициенті.

Бұл теңдеулерге (1. 41), (1. 1-1. 4) болжамдарға сүйене отырып, гипосерпімді пластикалық ортаны сипаттайтын анықтауыш теңдеулерді қосу керек. Эйлер айнымалылары арқылы ол теңдеулерді былай жазуға болады:

1. Кернеулерді анықтайтын Гук заңы

$\ \ \ \ \ \ \ \frac{D\sigma_{ij}}{Dt} = \frac{d\sigma_{ij}}{dt} + \mathrm{\Omega}_{ik}\sigma_{kj} + \mathrm{\Omega}_{ki}\sigma_{kj} = D_{ijkm}\left( \dot{ɛ_{km}} - {\dot{ɛ}}_{km}^{p} \right) + \mathrm{\Omega}_{ik}\sigma_{kj}{+ \mathrm{\Omega}}_{ki}\sigma_{kj}\ \ \ \$ (1. 42)

Мұндағы $\frac{D\sigma_{ij}}{Dt}$ - Яуманның туындысы, $D_{ijkm} -$ материалдың серпімділік модульдерінің тензор ы, $\mathrm{\Omega}_{ik} -$ иірімділік (қүйын) тензоры. 2. Изотропты орта үшін пластикалық шарт:

$\ \ \ \ \ \ \ \ F\lbrack I_{i}(\widehat{\sigma}$ ), $I_{i}\left( \widehat{\dot{\varepsilon}} \right), L_{K}\rbrack = 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 43)

мұндағы $I_{i}(\widehat{\sigma}$ ) - кернеу тензорынын инварианттары, $I_{i}\left( \widehat{\dot{\varepsilon}} \right)$ пластикалық деформация жылдамдықтарының тензорының инварианттары, Lk - дененің ішкі параметрлері.

3. Ағузаңы $έ_{ij}^{p} = \dot{\lambda}\frac{\partial F}{\partial\sigma_{ij}}$ (1. 44)

F - пластикалық потенциал (1. 44)

4. Ортаның ішкі құрылымын, беріктенуін, зақымдануын, кеуектенуін сипаттайтын параметрлерді анықтайтын эволюциялық теңдеулер

${\dot{L}}_{k} = f_{k}\lbrack I_{i\ }\left( \widehat{\sigma} \right), L_{k}\rbrack$ (1. 45)

бұл жерде нүкте арқылы уақыт бөйынша материалдық туынды белгіленген.

Жоғарыда келтірілген теңдеулер (1. 41) -(1. 45) ыдырату əдісі қолданатын теңдеулер түрінде [6. 156 бет] жазылған. Ортаның сақталу заңдарын (1. 41) ыдырату үшін Г. И. Марчуктың əдісін пайдалануға болады.

Енді серпімдіпластикалық теңдеулерге (1. 42) -(1. 45) ыдырату (декомпозиция) əдісін пайдаланамыз. Оңай болу үшін: T=const; $ɛ_{ij}$ «1; $\mathrm{\Omega}_{ij} = 0. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 46)

Ыдыратудың жалпы схемасы былай болады. Ыдыратуды тек (1. 42) теңдеуге қолданамыз, бұл формуладағы жалпы деформация жылдамдығы (1. 46) анықталады ${\ \ \ \ \ \ \ \ \ \ \ \ έ}_{ij}^{} = \frac{1}{2}\left( v_{i, j} + v_{j, i} \right),$ (1. 47)

мұндағы ν k - бөлшектердің жылдамдығы, ал үтір арқылы Эйлер айнымалылары бойынша дербес туындылар белгіленген. Предиктор (predictor) $έ_{ij}^{P}$ = 0 кезінде қолданылады. Бұл жағдайда ортаның материалы серпімді, сондықтан ∆t аралығында серпімді есепті шешу қажет:

$\ \ \ \ \ \ \ \rho\frac{\partial v_{i}}{\partial t} = \sigma_{ij, j},$

$\frac{\partial\sigma_{ij}}{\partial t} = \frac{1}{2}D_{ijkm}$ ( $v_{k, m} + v_{m, k}) . \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 48)

Бұл жүйенің (1. 48) бастапқы шарты түрінде толық серпімдіпластикалық есептің алдыңғы адымындағы шешімі пайдаланады. Корректор (corrector) (1. 42) теңдеуде $έ_{ij}^{}$ = 0 кезінде қолданылады.

Бұл жағдайда (1. 42) жəне (1. 44) қатынастарынан кернеулердің релаксациясын анықтайтын теңдеулер шығады $\frac{\partial\sigma_{ij}}{\partial t} = - \frac{d\lambda}{dt}D_{ijkm}\frac{\partial F}{\partial\sigma_{km}}$ . (1. 49)

Релаксация процесі пластикалық шарттың тұрақты мəніне жеткенше орын алады.

Классикалық серпімдіпластикалық орта жағдайында, (1. 49) жəне (1. 46) теңдеулердегі уақыт t жойып жəне λ айнымалысына көшуге болады: $\ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial\sigma_{ij}}{\partial t} = - D_{ijkm}\frac{\partial F}{\partial\sigma_{km}}.$ (1. 50)

Енді (1. 50) жəне (1. 48) теңдеулерін мына бастапқы шартты λ= $\lambda_{0}$ , $\sigma_{ij}$ = $\sigma_{ij}^{e}$ , $L_{K}$ = $L_{K}^{e}$ пайдаланып шешеміз:

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{ij} = \sigma_{ij}($ λ, $\sigma_{ij}^{e}, \ L_{K}^{e}$ ), $L_{K} = L_{K}($ λ, $\sigma_{ij}^{e}, \ L_{K}^{e}$ ) . (1. 51)

Табылған шешімдерді (1. 51) пластикалық шартқа (1. 43) қойып, белгісіз шаманы λ - табуға теңдеу аламыз:

F[ $I_{i}(\lambda), \ L_{i}(\lambda), L_{i}^{e}, I_{i}^{e}$ ] =0 (1. 52)

Бұл теңдеуден (1. 52) λ тауып, оныңмəнін (1. 53) апарыпқойып, есептің толық шешімін табамыз.

Егер пластиқалық шарт дифференциалдық түрде болса, онда (1. 51) шартынан λ анықтау үшін төмендегі дифференциалдық теңдеуге келеміз. ${\ \ \ \ \ \ \ \ \ \ \ F}_{1}(\sigma_{ij, \ }^{e}L_{k, }^{e}\lambda, \dot{\lambda) = 1. }$ (1. 53)

Бұлтеңдеуден (1. 53) $\lambda^{*}$ - табамыз

$\ \ \ \ \ \ \ \ \ \ \ \frac{\tau d\lambda}{dt} = ɸ(F) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$ (1. 54)

Мұндағы τ - релаксация уақыты, φ(0) =0. Бұл теңдеудің (1. 54) шешімін аналитикалық түрде жазуға болады.

2. 2-ЕСЕП. СЕРПІМДІ АЙМАҚТА ШЕКАРАЛЫҚ ЕСЕПТІ ТАЛДАУ

Пластикалық аймақ серпімді аймақ

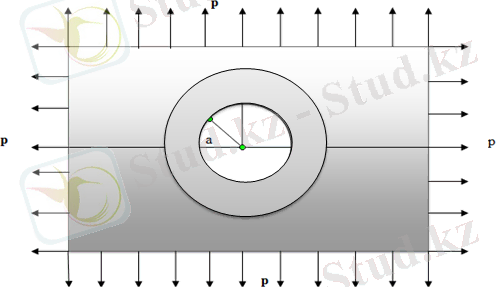
2 сурет- Дөңгелек қуысы бар пластина.

${\ \ \ \ \ r}_{T} < r < \infty$ , $r_{T} \geq a$ интервалын қарастырамыз. Кернеуді келесі түрде аламыз [4] :

("p" және "е" индекстары сәйкесінше кернеудің пластикалық және серпімді аймақтарға байланысты жазылады. )

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sigma}_{r}^{e}$ = $\frac{2}{\sqrt{3}}\sigma_{T}$ (A- $\frac{B}{r^{2}}$ ) ; ${\ \ \ \ \ \ \sigma}_{\theta}^{e}$ = $\frac{2}{\sqrt{3}}\sigma_{T}$ (A + $\frac{B}{r^{2}}$ ) ; $\sigma_{z}^{e}$ =0. (2. 1)