Тұтқырлы пластикалық сұйықтың керек ортадағы қозғалысын жылжымалы шекарасы бойынша сандық зерттеу

КІРІСПЕ4

1 Тұтқырлы пластикалық сұйықтың (TПС) ФИЛЬТРАЦИЯСЫНЫҢ КЕЙБІР МЕХАНИКАЛЫҚ МОДЕЛДЕРІ. НЕГІЗГІ ТЕҢДЕУЛЕРІ МЕН ҚАТЫНАСТАРЫ9

1. 1 Полигональды аппроксимация. Модель1. 12

1. 2 Гиперболалық аппроксимация. Модель. 216

2 СУТЕГЕУРІНДІ РЕЖИМ КЕЗІНДЕ ОРНАТЫЛҒАН ФИЛЬТРАЦИЯ. НЬЮТОНДЫҚ ТПС-ТЫ ЫҒЫСТЫРУ17

2. 1 Түзу сызықты-параллелді ағыс18

2. 2 Жазық тарамдалған ағыс29

3 ТПС-ҚА БІРТЕКТІ КЕУЕК ОРТАДАҒЫ ЕСЕП ҚОЮ39

3. 1Есеп № 139

3. 2 Есеп № 245

4 ТҰТҚЫРЛЫ-ПЛАСТИКАЛЫҚ СҰЙЫҚТЫҢ КЕУЕК ОРТАДАҒЫ САНДЫҚ ШЕШІМІН ҚАРАСТЫРУ47

4. 1 Тұтқырлы-пластикалық сұйықтың кеуек ортадағы ағысын сандық зерттеу47

4. 2 Жылжымалы шекараны торлық түйініне аулау47

4. 3 Сандық санаудың тура өту әдісі49

4. 4 Екі торлық әдісті қолдану51

5 БАСТАПҚЫ ҚЫСЫМ ГРАДИЕНТІ АЙНЫМАЛЫ БОЛҒАНДАҒЫ САНДЫҚ НӘТИЖЕЛЕРІНЕ ТАЛДАУ53

ҚОРЫТЫНДЫ58

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ59

Сансыз көп рет есептеулер мен лабораториялық тәжірибелік мәліметтер негізінде жылдамдық фильтрациясы қысым градиенті модулімен индикаторлық қисықты келесі түрде схематикалық бейнелеуге болады. $v = v(\nabla p)$ функциясы координат басынын абсцисса өсіне жантайлап барып, асимптоталық түрде монотонды өседі және мынадай қисық көрінісінде болады (1-сурет) .

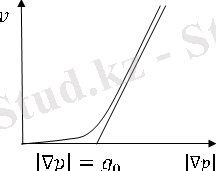
1-сурет - Сұйық жылдамдығының қысымға тәуелділігі

Қысым градиенті модулінің аз мәнінде бұл қисық абсцисса өсіне қарай аз ғана жантайып, жылжу градиенті деп аталатын кейбір қысым градиенті модулінің ( $\nabla p^{*} = g_{0})$ мәніне жетіп содан кейін жылдам өсе бастайды. Сондықтан келесі суретті көз алдымызға келтіруге болады. Қысым градиенті аз болғанда, сүзу қабатындағы қысым градиентінің айқын мөлшері байқалады. Ал қысым градиентінің үлкен немесе тең мәнінде, ТПС сүзу қабатында жылдам өзгерісті байқаймыз: сүзу жылдамдығы елеулі түрде өседі және оның қысым градиентіне тәуелділігі асимптоталық түрде сызыққа жақындайды. Жоғарыдағы айтылғандардың нәтижесінде индикаторлық қисыққа [1] әр түлі аппроксимациялау тәсілдерін қолдануға болады.

1953ж. А. Х. Мирзаджанзаде [2] феноменологиялық ТПС сүзу теориясын жылжу градиентімен сүзу пішіні негізінде ұсынды. Бұл пішінмен келісе отырып, тәжірибелік тәуелділік $v = v(\nabla p)$ асимптота графигімен сәйкес келетін және абсцисса өсінің оң бөлігіндегі кесіп алынған кесінді шамасы $\nabla p^{*} = \beta$ тең болатын жарты түзумен аппроксимацияланады. Қазіргі жағдайда Дарсидің сызықтық емес заңы мына түрде жазылыды:

$\overrightarrow{v} = \left\{ \begin{array}{r} 0, \ \ \ \ \ \nabla p \leq g_{0} \\ - \frac{k}{µ}\left( 1 - \frac{g_{0}}{\nabla p} \right) \nabla p, \ \ \ \nabla p > g_{0} \end{array} \right. \$ (к. 1)

Мұндағы $\overrightarrow{v} -$ сүзу жылдамдығы, $\nabla p -$ қысым градиенті, $k -$ өткізгіштік коэффициенті, $\mu -$ сұйықтың тұтқырлығы. Сайып келгенде, жылжу градиентімен сүзу пішінін қолданғанда сұйық ағысы тек қана пластың қысым градиенті кейбір өскен жағдайда ғана жүзеге асады. Сірә бұл пішінді қысым

болған жағдайдағы суреттегідей мәні сондай-ақ сүзіліс сыйпаттамасы өзгермеaген жағдайда сузілісті ескермеген жағдайда пайдалансақ болады. Егер қысым градиенті аз болғанда сұйықтың сүзілуі толығымен сүзілу суретіне айқын әсер етеді, сондықтан бұл жағдайда қысым градиенті $\nabla p$ аз болғандағы сұйық ағысын ескеретін сүзу пішінін қолданған жөн.

Көрсетілген пішінге, мысалы, индикаторлық қисыққа $v = v\left( \nabla p \right) \ \ \lbrack 1, \ 6\rbrack$ полигоналдық және гиперболалық аппроксимацияны қолдансақ және көрсетілген пішінге апарып қойуға болады. Сонымен бұл полигон индикаторлық қисықта бірінші бөлімінде координат басынан өтетін және қысым градиенті аз болғандағы сүзілісті сипаттайды, ал екінші бөлімінде асимптота графигімен $v = v\left( \nabla p \right)$ сәйкес келетін және қысым градиенті үлкен болғандағы сұйықтың ағысын сипаттайды. Индикаторлық қисықты гипперболалық аппроксимациялау кезін де координат басына орналастырады. Ал гиперболаның асимптотасы асимтотамен $v = v\left( \nabla p \right)$ функциясының графигі бірігеді. 2- сурет, полигон пунктир сызықтармен, ал гипербола және оның асимптотасы түзу сызықтармен көрсетілген. Индикаторлық қисық суретте пунктир штрихтармен бейнеленген.

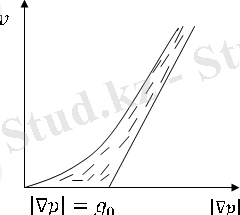
2-сурет - Сұйық жылдамдығының қысымға тәуелділігі

Индикаторлық қисықты полигональдық және гиперболплық аппроксимациялауға негізделген сүзу пішіні үшін сүзу жылдамдығы сәйкесінше келесі түрде жазылыды:

$\overrightarrow{v} = \left\{ \begin{array}{r} - \frac{k}{\mu}\nabla p, \ \ \ \ \ \nabla p < \beta \\ - \frac{k}{µ}\left( 1 - \frac{\beta\mu_{0}}{\nabla p} \right) \nabla p, \ \ \ \nabla p > \beta \end{array} \right. \$ (к. 2)

$\overrightarrow{v} = - \frac{k}{µ}\lbrack\sqrt{\beta^{2} + (\nabla p) } - \beta\rbrack\frac{\nabla p}{\nabla p}$ (к. 3)

Мұндағы $\mu_{0} = 1 - \frac{\mu}{\upsilon}$ , $v -$ қысым градиенті аз болғандағы ТПС тұтқырлығы. Серпінді, сонда әдеттегідей,

$m\gamma = \gamma_{0}\lbrack m_{0} + \beta^{*}(p - p_{0}) \rbrack$ (к. 4)

мұндағы $m -$ кеуектілік коэффициенті, $\gamma -$ сұйықтың тығыздығы, $m_{0}$ және $\gamma_{0} -$ дің мәндері кеуектілік коэффициенті және қысым $p_{0}, \ \beta^{*} -$ пластың серпінді сығылуы кезінде сәйкес келетін коэффициент. Енді узіліссіздік теңдеуін сузілген ағымға қолданамыз:

$div\left( \gamma\overrightarrow{v} \right) = - \frac{\partial}{\partial t}(m\gamma)$ (к. 5)

(к. 1), (к. 2) және (к. 3) сүзу заңынан сәйкесінше әрбір сүзу пішінінен серпімді пластағы қысымды анықтау үшін келесі дифференциялдық теңдеулерді аламыз:

$ædiv\left\lbrack \left( 1 - \frac{g_{0}}{\nabla p} \right) \nabla p \right\rbrack = \frac{\partial p}{\partial t}\, \ \ \ \ \nabla p > g_{0}$ (к. 6)

$ædiv\left( \frac{\mu}{p}\nabla p \right) = \frac{\partial p}{\partial t}$ , $\nabla p < g_{0}$ (к. 7)

$ædiv\left\lbrack \left( 1 - \frac{g_{0}\mu_{0}}{\nabla p} \right) \nabla p \right\rbrack = \frac{\partial p}{\partial t}\, \ \ \ \ \nabla p > g_{0}$ (к. 8)

$ædiv\left\lbrack \left( \frac{\sqrt{g_{0} + {(\nabla p) }^{2}} - g_{0}}{\nabla p} \right) \nabla p \right\rbrack = \frac{\partial p}{\partial t}\ .$ (к. 9)

Әрбір келтірілген дифференциялдық теңдеулерді нақты сүзу есебін шешетін кезде есептің сипаттамасынан шыққан қарапайым бастапқы және шекаралық шарттардың орнына қоюға болады. Сонымен қатар жылжу градиентімен сүзу пішініндегі есепті шығару барысында сүзудің құбылмалы облысы пайда болады, және бұл облыстағы шекрада әзірге ол пластың шекарасына жетпейді, себебі қысым градиентінің модулі жылжу градиентіне, ал қысым - бастапқы пластың қысымына тең болуы керек. Егер индикаторлық қисықты полигональдық және гиперболалық аппроксимациялауға негізделген есепті, сүзу пішінін пайдаланып шығарсақ, сүзу облысында қысым градиентінің модулі қысым градиентінің нақты мәніне теңболатын, ал одан кіретін қысым үзіліссіз ауысатын жылжымылы шекара пайда болады. Сұйықтар мен газдардың сызықты емес уақытқа тәуелді жағдайындағы теориялық жұмастарға қысқаша мәлімет береміз.

А. Х. Мирзаджанзаденің, М. Т. Абасованың [4] жұмысында жартылай шексіз пластағы тұтқырлы сұйықтың тұтқырлы-пластикалық ығысуы қарастырылған. Ал шешімін алу үшін уақыттан тәуелсіз жүйеге алмасатын әдіс қолданылады. ыыы

[5] жұмыста галлереядағы шығын тұрақты болғандағы сүзудің узік сызықты заңы түзу сызықты сүзілген ағымдағы қысым үшін теңдеудің автопішінді шешімін алуға қолайлы жағдай туғызды. Жоғарыда айтылған теңдеу шешімі оңашаланған кескінде табылған екі қарапайым сызықтық теңдеуден тұратын жүйеге қоямыз. Шекаралық өткелде схеманың жылжымалы градиенті үшін шешім табылған.

[7] жұмыста, серпімді күйдегі және скважинаның дебиті тұрақты болғандағы шексіз пласта бірлік скважинаға ағатын сұйық қарастырылады. Интегралдық қатынас [6] әдісімен біреуі жылжу градиентімен пішіндеуге келетін сүзілістің екі сызықтық емес заңы үшін есептің асимптоталық шешімі алынған. Ары қарай қысым өзгерісі жүріп жатқан қисықты бақылаумен сүзу заңының параметрлерін анықтау жүзеге асырылады.

Жылу градиенті және дебитпен алынған пішін үшін [11] жұмыста шексіз пластағы, жазық радиалды сүзу бірлік скважинада $\sqrt{t}$ - ға пропорционал болатын есеп қарастырылады. Есептің автопішінді шешімі қатар түрінде, ал жуық шешімі интегралдық қатыныс арқылы алынған және олардың жақсы сәйкестігі үйлесімді интервал ішінде екендігі көрсетілген. Ары қарай екі мүшелік (пораболалық) сүзу заңы қарастырылады. Есептің автопішінділігі оны жуық шешімі сонымен қоса интегралдық қатынас әдісі арқылы табылған екі қарапайым теңдеуден тұратын жүйенің шешіміне апарып қоюымызға болады.

С. А. Агаеваның [4] жұмысында, түзусызықты галлереяда немесе скважинада қысым $\sqrt{t}$ - ға пропорционалды өзгергендегі сұйықтың сүзілісі кезіндегі бастаптқы градиенттің автопішінді шешімі алынған.

Жылжу градиентімен сұйықтың сүзілуі есебі үшін [3] жұмысы қарастырылады. Ньютондық емес мұнайдың фильтрациясы тәжірибелік зерттеу негізінде өндіріс шартындағы жылжу градиентінің анықталу әдісі қолданылады. Галереяға сұйықтың белгілі бір бөлігі құйылып жатқан жағдайда тұрақты қысым берілгенде жылжу градиентімен сығылатын ТПС-тың фильтрациялануы есебінің шешімін интегралдық қатынас есебін пайдаланып алған.

[1, 2] жұмыстарда материалдық баланс қатынасынан шыққан шарт жылжымалы шекарада сызықтық емес заң бойынша сұйықтың фильтрациясы кезінде ашық және жабық зоналарға болінеді. Бұл қатынастар серпімді күйдегі ТПС [1, 3] есебінің жуық шешімін алу әдісін құру үшін пайдалы болып шықты. Қатардың келтірілген сандық мәні қарапайым негізгі ТПС [3] фильтрациясы есебінің жуық шешімімен сәйкес келеді.

[7] жұмыста серпімді әлсіз сығылатын сұйық фильтрациясының уақытқа тәуелділігі теорисынан t үлкен болғанда Коши есебін шешу асимптоталық жағдайы қарастырылады. Бұл асимптотика екінші турдегі автопішінді шешім болып анықталады - ол үшін автопішіндік айнымалы өрнегінің дәрежелік көрсеткінің шамалық ұғынысымен емес, қарапайым дифференциалдық жүйені шешу барысындағы шешімді есептің шешіміне қою арқылы табылады. Сонымен автопішіндік айнымалы кейбір тұрақты сан болып табылады, жалпы айтқанда, интегралдық сақталу заңын пайдаланып табу мүмкін емес, автопішіндік бастапқы шартты пайдаланып сандық мәнін табу керек.

Уақытқа тәуелді газдың скважинаға ағымы есебінің жуық шешімі [10] жұмысында кедергі заңынан алынған; [9] жұмыста осындай уақытқа тәуелді заң үшін газдың фильтрациясы есебінің автопішінді жағдайы қарастырылған.

[4] жұмыста қатар негізіндегі тәжірибелерден газ фильтрацияланғандағы сызықтық әсер көріністері орнатылған, сонымен қатар, фильтрация заңы (жылжу градиентімен) шектік градиент моделімен жақсы жазылды. Сонымен қатар тәжірибелердің бірінде фильтрацияның сызықтық емес заңы анықталған, сондай-ақ гиперболалық немесе полигональдық модельдер [4] -ке қарағанда жақсы көрсетілген. Шектік градиентті модельдегі есептің шешімін интегралдық қатынас әдісін пайдаланып галереядағы газдың ағымын оған қысым берілгенде жуықталып шешілген.

[1, 3, 5, 9] жұмыстарда ТПС фильтрациясына арналған жылжу градиентінің қойылымын пайдалану ұсынысы қарастырылған. Сонымен қатар, мұнайдың құрылымды- механикалық қасиеті шекарада бір бастапқы шыққан орнында бірдей болмайды [1-3] . Сондай-ақ қазіргі заманғы практикада мұнай шығатын орындарда пластың үлкен көлемді үстіңгі салқын су қабатына шайқау әдісі кеңінен қолданылады, бұл елеулі түрде бастапқы шыққан жылы орнын білдіреді. Бұл өз жағынан ТПС- тың және фильтрация [7] шартының қасиетінің мәндерін өзгертеді. Сондақтан айнымалысы бар жылжымалы градиентті есепті теориялық және практикалық жағынан да қарастыруға қызуғушылық туады.

Есептің физикалық қойылымы .

Бірдей, изотропты, бірлік күшті және ені жартылай шексіз (немесе бірлік күшті, шексіз, разбуренный бір скважинада) пласт жылжымалы градиентті ТПС- пен толтырылған және кеңістік координатасынан тәуелді. Сұйық сығылатын сұйық болсын, онда пластағы қысым эксплуатацияланғанға дейін тұрақты және $p_{0}$ - ге тең болады. Уақыттың бастапқы моментінде пластың сол жақ соңында эксплуатацияланған галерея (эксплуатацияланған скважина радиусы $r_{c} \geq 0$ ), забойда немесе тұрақты қысымда тұратын немесе тұрақты дебитпен жұмыс істей бастайды. Сұйық жылжу градиентіне ие болып пласта екі зонаға бөлінеді: фильтрация зонасы және зона оның жоқ болуы, шекара бөлім аралығына $\ l = l(t) ; \ l(0) = 0\ \ (l(0) = r_{c} \geq 0)$ заңы бойынша бірте-бірте орналасады. Cұйық пластың берілген нүктесі үшін сыпатталған құрылымды-пластикалық қасиетке ие болады.

Бұл тарауда ТПС фильтрациясының кейбір механикалық моделдері қарастырылады, бұл модельдер фильтрация жылдамдығының моделі мен қысым градиенті арасындағы эксперименталды(тәжірибелі) алынған тәуелділіктің белгілі өңдеуімен шартталған. Әрбір фильтрация моделінің шегінде фильтрация заңы(Дарси заңының аналогы) орнатылады, ола келешекте не қабаттың өткізгіштігі бойынша біртекті еместікпен, не сұйықтың әр түрлі қасиеттерімен байланысты, негізгі қатынастарды алу мен қабаттың серпінді және су тегеурінді(водонапорный) режимі жағыдайында қысымды анықтау үшін дифференциялдық теңдеулерді шығару үшін қолданылады.

$1^{0}$ . А. Х Мирзаджанзаде [10] ТПС феноменологиялық сүзу теориясы эксперименталды(тәжірибелі) мәліметтерді өңдеу $v = v(\nabla p)$ тәуелділігін түзу сызық түрінде көрсетуге негіз берді, ол абцисса өсінің оң жақ бөлігінде $\nabla p^{*} = \beta$ тең кесінді кесіп өтеді(1-сурет) . Бұл Мирзаджанзадеге ТПС фильтрациясының мынадай механикалық моделін ұсынуға мүмкіндік берді, ол үшін фильтрация заңы, Дарсидің жалпыланған заңы деп аталған, келесі түрде жазуға болады.

$\overrightarrow{v} = \left\{ \begin{array}{r} 0, \ \ \ \ \ \nabla p \leq g_{0} \\ - \frac{k}{µ}\left( 1 - \frac{\beta}{\nabla p} \right) \nabla p, \ \ \ \nabla p > g_{0} \end{array} \right. \$ , (1, 1)

Мұндағы $\overrightarrow{v} -$ сүзу жылдамдығы, $k -$ өткізгіштік коэффициенті, $\mu -$ сұйықтың тұтқырлығы $\beta -$ қысым градиенті, ол жылжудың (сдвига) шектік кернеуінен өту үшін керек, $\nabla = \frac{\partial}{\partial x}$ $\overrightarrow{i}$ + $\frac{\partial}{\partial y}$ $\overrightarrow{j}$ .

1-сурет

Дәл сол жерде ТПС-тың сызықты фильтрациясы кезінде β шектік градиентінің мәні мына қатынаспен

β = ${\nabla Ρ}_{кр}$ = $\frac{{a\tau}_{0}}{\sqrt{k_{0}}}$ (1. 2)

анықталатыны белгіленген, мұндағы $\tau_{0}$ -шектік жылжу кернеуі, $\ k_{0}$ -ауа өткізгіштік коэффиценті, $\ a$ -белгілі тұрақты.

Осылайша ТПС фильтрациясы бастапқы жылжу градиенті бар ағыс моделін қолданған жағыдайда тек қысым градиенті белгілі бір шектік мәннен асқандағы обылыстарда ғана орындалатын болады, фильтрация моделін бастапқы жылжу градиентімен қолдана отырып [13-21] авторлар ТПС фильтрациясының дәл сол немесе басқа қойылымда кейбір есептерін шешкен болатын.

$2^{0}.$ келесілері анығырақ, керек ортада ТПС ағысы бойынша тәжірибелер аз ғана фильтрацияның болатынын анықтады және қысым градиенттері кезінде шектік шамадан төмен.

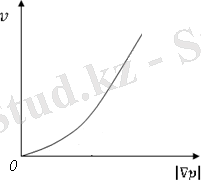
2-сурет

Бұл жағдай $\vartheta = \vartheta$ ( $\nabla p$ ) тәуелділігі 2-суретте схематикалық кескінделген монотонды өспелі функциямен түсіндіруге (интерпретировать) мүмкіндік береді, бұл функция координата басы арқылы өтеді және абсица өсіне көлбеу асимптотасы бар. Онда келесі фильтрация суретін (картинасын) елестетуге болады. Аз қысым градиенті кезінде кеуек орта оте аз не елеусіз сұйық ағысы орын алады, бұл құбылыс қысым градиентінің белгілі (шектік) мәніне дейін қаралады. Қысым градиенті шектік мәніне жеткенде және одан асқанда ТПС фильтрациясында сапалық және сандық өзгерістер байқалады, фильтрация жылдамдығы күрт артады және қысым градиентінен түзу сызықты тәуелсіздікке асимптоталық шығады.

Алынған $\vartheta = \vartheta$ ( $\nabla p$ ) эксперименталды(тәжірибелі) тәуелділігінен ТПС фильтрациясының басқада механикалық моделдер қатарын ұсынуға болады.

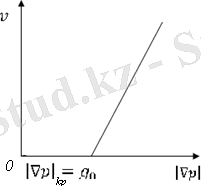
$3^{0}$ . модель1. $\ \vartheta = \vartheta$ ( $\nabla p$ ) графигі координаталар басынан өтетін белгілі бір қисықтықпен аппроксимацияланады. Бұл қисықтықтың бірінші бөлігі (AB) ТПС фильтрациясын қысым градиентінің аз кезінде сипаттайды, ал екінші (BC) қысым градиентінің көп кезінде көрсетілген $\vartheta = \vartheta$ ( $\nabla p$ ) қисығының полигоналды (полигональная) аппроксимацияланады 3-суретте үздік сызықтармен көрсетілген.

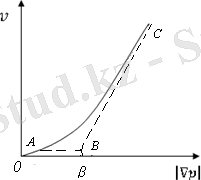
3-сурет

Осылайша ТПС фильтрациясының 1 моделі негізінде келесі жатыр: қысым градиентінің аз шамасы кезінде (шектік жағыдайға дейін) ТПС ағысы кеуек ортада Дарсидың сызықтық заңы бойынша жүреді, ал қысым градиентінің үлкен мәндері кезінде (шектік жағыдайдан жоғары) ТПС фильтрациясы Дарсидың жалпыланған заңы бойынша жүзеге асады[4. 8] .

Модель2. $\ \vartheta = \vartheta$ ( $\nabla p$ ) функциясының графигі, қысым градиенті өзінің шектік мәнінен асып кетсе, түзу сызыққа асимптотикалық шығатын жағдайн ескеріп, оны сәйкес асимптотасы бар монотонды өспелі белгілі бір сызықпен аппроксимациялауға болады. ондай қисық ретінде шамасы, төбесі координата басында жататын және асимптотасы қысым градиентінің үлкен мәндері кезінде $\ \vartheta = \vartheta$ ( $\nabla p$ ) функциясының графигі шығатын түзумен сәйкес келетін гиперболаны алған ыңғайлы.

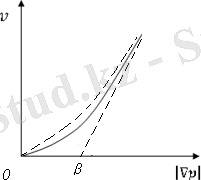
4-сурет

4-суретте бұл гипербола және оның асимптотасы үзік сызықпен бейнеленген.

Жоғарыда ұсынылған $\vartheta = \vartheta$ ( $\nabla p$ ) функция графигінің аппрокцимациясының екі тәсілімен бірге басқалары да болуы мүмкін[4. 8], оны мысалы, координаталар басы арқылы өтетін қайсыбір дәрежелік немесе көрсеткіштік функциямен аппрокцимациялауға болады.

$1^{0}$ . Жоғарыда көрсетілгендей полигональды аппроксимация кезінде $\vartheta = \vartheta$ ( $\nabla p$ ) тәелділік графигі координата басынан өтетін белгілі бір қисықтықпен алмастырылады. Бұл қисықтықтың теңдеуін мына түрде келтіруге болады:

$\nabla p$ < $\beta$ кезінде, $\vartheta = d_{2}\nabla p$

$\nabla p$ >β кезінде, $\vartheta = d_{0}$ + $d_{1}\nabla p$ .

$d_{0}, d_{1}$ және $d_{2}$ параметрлері келесі түсініктерден анықталады. AB түзуі координата басынан өтетін болғандықтан (сурет 3 ті қара) және де аз қысым градиенті кезінде ТПС фильтрациясын кеуек ортада сығылмайтын сұйық ағысы кезінде Дарсидың сызықты заңына ұқсас сипаттайтын болғандықтан, онда $d_{2} = \frac{k}{\nu}$ өрнегін қабылдау табиғи, мұнда $\nu$ -аз қысым градиенті кезіндегі ТПС тың динамикалық тұтқырлығы. Ары қарай BC түзуі ТПС фильтрациясын үлкен қысым градиентінде спаттайды, бұл кезде кеуек ортада сұйық ағыны Дарсидың жалпылнған заңына бағынады(1. 1) . онда бұл түзудің бұрштық коэффиценті $\frac{k}{\eta}$ -ге тең болады, яғни $d_{1} = \frac{k}{\eta}$ .

$d_{0}$ параметрі ТПС фильтрациясының жылдамдығының үзіліссіздік шарты бойынша қысым градиенті шектік шамаға тең кезде ( $\nabla p = {\nabla p}_{кр} =$ β ) оңай анықталады, онда

$\frac{k}{\nu}$ β $= d_{0} + \frac{k}{\eta}$ β .

Осы жерден $d_{0} = - \frac{k}{\eta}$ β $\eta_{0}$ , мұнда $\eta_{0} =$ 1 $- \frac{\eta}{\nu}$ . Осылайша

$\vartheta = \frac{k}{\nu}\nabla p$ , $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \nabla p$ < $\beta$ кезінде.

$\vartheta = \frac{k}{\eta}$ ( $\nabla p -$ β $\eta_{0}$ ) $\nabla p$ >β кезінде.

Демек, қарастырылып отырған ТПС ағысының моделінде кеуек ортаға фильтрация жылдамдығы былай жазылады:

$\vartheta = - \frac{k}{\nu}\nabla p$ , $\ \ \nabla p$ < $\beta$ кезінде (1. 3)

$\vartheta = - \frac{k}{\eta}(1 - \frac{\beta\ \eta_{0}}{\nabla p}\ ) \nabla p$ , $\ \nabla p$ >β кезінде (1. 4) .

$2^{0}$ . Түр (порода) серіппелі болсын, ал ТПС тамшылы-сығылмалы сүйық класына жататын болса, онда

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс