Stud.kz

Хаосты радиотехникалық генераторлардың жасыру деңгейін анықтау


Пән: Электротехника
Жұмыс түрі:  Дипломдық жұмыс
Тегін:  Антиплагиат
Көлемі: 38 бет
Таңдаулыға:   

Мазмұны

кіріспе . . . 4

  1. Хаос генераторлары . . . 6Ляпунов көрсеткіші . . . 6Логистикалық бейнелеу генераторы . . . 7Хенон бейнелеу генераторы . . . 9Жинақталу және лақтыру генераторы . . . 11Чуа генераторы . . . 13Ван-дер-Поль генераторы . . . 16Лоренц генераторы . . . 17Анищенко-Астахов генераторы . . . 18
  2. СИГНАЛ ШУЫЛ ҚАТЫНАСЫН АНЫҚТАУДЫҢ ЖАҢА ӘДІСІ . . . 21
  3. СИГНАЛ ШУЫЛ ҚАТЫНАСЫН КЛАССИКАЛЫҚ ЭНЕРГИЯ ӘДІСІМЕН ТАБУ . . . 24
  4. САНДЫҚ ТӘЖІРИБЕ НӘТИЖЕЛЕРІ . . . 25Хаос кезінде сигнал шуыл қатынасының параметрге тәуелділігі . . . 25Сигнал мен хаосты қосқан кездегі әртүрлі амплитудағы сигнал шуыл қатынасының параметрге байланысы . . . 29Классикалық энергия әдісімен сигнал шуыл қатынасының параметрге тәуелділігі . . . 37Сигнал шуыл қатынасының және классикалық сигнал шуыл қатынасының (энергия әдісімен) параметрге тәуелділігі . . . 41Сигнал шуыл қатынасының классикалық сигнал шуыл қатынасына (энергия әдісімен) тәуелділігі . . . 45

ҚОРЫТЫНДЫ . . . 50

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 51

КІРІСПЕ

Динамикалық хаос дыбыстық сигналды жасыру үшін, яғни ақпаратты қорғау мақсатында қолданылады. Дыбыстық сигналды хаоспен жасыру үшін, құрылымы жағынан қарастырып отырған сигналымызға ұқсас хаос таңдауымыз керек. Динамикалық хаос тиімді технологияларды жіберу үшін қолданады.

Қазіргі заманғы байланыс жүйелері ақпаратты тасушы ретінде гармоникалық тербелістерді қолданады. Таратқыштағы ақпараттық сигнал бұл тербелістерді амлитудасы, жиілігі немесе фазасы бойынша модуляциялайды, ал қабылдағышта ақпарат кері операция көмегімен бөлініп алынады, яғни демодуляция арқылы. Ақпарат тасушының модуляциясы гармоникалық тербелістерге түрленген модуляция есебінен жүзеге асады немесе тербелістерді түрлендіру процесіндегі генератордың параметрлерін басқару жолымен.

Хаосты сигналды ақпараттық сигналмен модуляциялауға болады. Бірақ мүмкіндіктері әлдеқайда көп болады. Егер гармоникалық тасушының сипаттамалары тек үшеуімен ғана басқарылатын болса (амплитуда, фаза, жиілік), онда хаосты тербелістер кезінде параметрдің кішкене өзгерісінің өзі тербелістің сипаттамасын сенімді түрде өзгертеді. Бұл дегеніміз, параметрмен өзгеретін хаос көздері ақпараттық сигналды хаосқа және хаосты сигналды ақпараттық сигналға модуляциялайтын кіріс тізбектердің кең ауқымына ие. Одан бөлек, хаосты сигналдар кең жолақты, керек болса аса кең жолақты болып келеді. Радиобайланыс жүйесінде тасушы сигналдың жиілігінің кең жолағы ақпаратты жіберу жылдамдығын көбейту үшін қолданылады, сонымен қатар жүйенің тұрақтылығын арттыру үшін .

Хаосты сигналдар жіберіліп отырған ақпаратты жасыру үшін де мысалы: құпия (жасырын) байланыс ұйымдары үшін қолданылады. Ақпаратты хаосты сигналға енгізудің тиісті бағытын таңдаған кезде, қабылдағыштағы сигналдың пайдалы құраушысын қалпына келтіру тіпті хаосты тасушы шуыл деңгейінен төмен орналасса да жүзеге асады, демек мәселе ақпаратты ғана жасыруда емес, сонымен қатар оны жіберу фактілеріне де байланысты болады. Егер де хаосты сигналды рұқсат етілмеген түрде оның ішінен ақпаратты қалпына келтіру үшін хаосты тербелістер генераторының нақты құрылымын және хаосты тербелістің модуляция әдісін білу керек. Оны білмейінше пайдалы сигналды яғни ақпаратты қалпына келтіру мүмкін емес.

Диплoмдық жұмыcтың мақcаты - қазіргі таңдағы қауіпсіз ақпарат таратуды және қабылдауды қамтамасыз ету, яғни ақпаратты жіберуде жасыру деңгейін қаншалықты тиімді етіп қолдану керектігін анықтау. Ол үшін біз хаос генераторларында тәжірибе жүргізіп, бірінші - ең тиімді, жасыру деңгейі жоғары хаосты генераторды анықтау. Анықталған хаосты генератордың артықшылықтары мен кемшіліктеріне тоқталып өту және бізге тиімді екендігін дәлелдеу.

Диплoмдық жұмыcтың өзeктілігі. Хаос генераторларын жан-жақты зерттеп, оларды еліміздің құпия (жасырын) байланыс ұйымдарында қолдану және ақпарат таратудың қауіпсіздігін қамтамасыз ету болып табылады.

Диплoмдық жұмыcтың ғылыми жаңалығы. Хаосты тербелісті радиотехникалық генератордың жасыру деңгейінің тиімділіғін арттыру жолдарын қарастыра отырып, хаосты генераторлардың ішінен барынша үлкен жасыру қабілетіне ие хаосты генераторды анықтау болып отыр.

Жұмыcтың тeopиялық жәнe тәжіpибeлік маңызы. Сандық тәжірибе нәтижелері, қорытындылары хаосты генераторлардың теориясын кеңейтеді, яғни қолдану аясының қаншалықты кеңдігін дәлелдейді. Жұмыстың теориялық маңызы - хаосты генераторлармен жеке-жеке танысу, олардың теңдеулерін, атқаратын қызметін, артықшылықтарын білуде маңызды, ал тәжірибелік маңызы - хаосты генераторлардың қайсысы тиімді екенін анықтауда алынған суреттерге сүйене отырып анықтай аламыз.

  1. ХАОС ГЕНЕРАТОРЛАРЫЛяпунов көрсеткіші

Хаосты тербелістердің ерекшелігі - жоғары сезімталдық, бастапқы шартқа аз өзгерту енгізгеннің өзінде сезеді. Жақын орналасқан траекториялар уақыт бойынша экспоненциалды өседі, басқа тұрақты траекторияларға қарағанда яғни тек сызықты өзгеретін траекторияларға қарағанда. Траекториялардың таралуы жүйе энергиясының шектеулігінде немесе жүйедегі диссипативті процесстердің салдарынан шексіз қозғала алмайды, соның нәтижесі хаосты тербелістердің пайда болуына алып келеді. Таралу жылдамдығының нақты сандық көрсеткіші Ляпунов көрсеткіші арқылы беріледі [1] .

Траекториялардың арақашықтығы мына (1. 1) - қатынаспен анықталады:

\[d_{n}=d_{0}\exp(n\mu\,)\]
. (1. 1)

Ляпунов көрсеткішінің оң мәні болып

\[\mathcal{M}\]
-локальді тұрақсыздық табылады. Басқару параметрінің мәндер аймағы Ляпунов көрсеткішінің оң мәніне сәйкес келуі хаосты режимге тең келеді. Ляпунов көрсеткіші көптеген басқарушы параметрлерді яғни хаосты қамтамасыз ететін басқарушы параметрлерді анықтау үшін қолданылады.

\[{\mathcal{X}}_{0}\]
-траекторияның
\[f^{(n)}(x_{0})\]
бастапқы мәні,
\[{\mathcal{N}}{\boldsymbol{\beta}}\]
-итерация өлшемі,
\[\overline{{{\oint}}}\]
-функция, бейнелеу беретін, ал
\[x_{0}=x_{0}+\varepsilon\]
-шағымдалған бастапқы мән,
\[\textstyle{\mathcal{C}}\]
-бастапқы қателік,
\[{\mathcal{X}}_{0}\]
-қателік немесе сәйкессіздік. Осы
\[X_{0}+\mathcal{E}\]
нүктеден
\[f^{(n)}(x_{0}+\mathcal{E})\]
траекториясы шығады. Итерацияның
\[\textstyle N\]
-ші қадамында
\[\textstyle\mid f^{N}(x_{0})-\mathbf{\nabla}f^{N}(x_{0}+\varepsilon)\mid\]
өлшемге бөлінеді, оны бастапқы қателік түрінде-
\[\textstyle{\mathcal{C}}\]
қарауға болады, кейбір коэффициентке көбейтілген:
\[\kappa e^{N/(x_{0})}\]
. Егер
\[\ell^{N\lambda}\left(x_{0}\right)\]
=1 болса, онда қателік итерацияның номерінің бойымен өзгермейді, ал
\[\ell^{N\lambda}\left(x_{0}\right)\]
>1- қателік өседі, ал
\[\ell^{N\lambda}\left(x_{0}\right)\]
<1- қателік азайады.

Бәрімізге белгілі

\[\ell^{N\lambda}\left(x_{0}\right)\]
=1 мынаған сәйкес
\[{\mathcal{A}}\left(x_{0}\right)\]
=0;
\[\ell^{N\lambda}\left(x_{0}\right)\]
>1 мынаған сәйкес >0;
\[\ell^{N\lambda}\left(x_{0}\right)\]
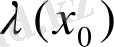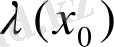<1 мынаған сәйкес <0;

Траекторияның экспоненциалды таралуының жылдамдығын анықтайтын көрсеткіш 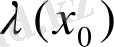, Ляпунов көрсеткіші деп аталады.

\[\textstyle\mid f^{N}(x_{0})-\mathbf{\nabla}f^{N}(x_{0}+e)\mid=e e^{N A\cdot(x_{0})}\]
. (1. 2)

Ляпунов көрсеткіші (1. 2) -формула бойынша көптеген дүниелерге қол жеткізе аламыз. Динамикалық жүйе, қадағаланып жатқан режим, аттрактордың әртүрлілігі және динамикалық жүйенің энтропиясы осының барлығына Ляпунов көрсеткіші арқылы қол жеткізе аламыз. Ляпунов көрсеткіші “фазалық траекторияның жақын бастапқы талаптармен таралу деңгейін сипаттайды” [1] .

Басқаша Ляпунов көрсеткішін уақыт бойынша ең жақын бастапқы мәнді екі реализациялық процесстің өзара корреляция жылдамдаған азайту сияқты анықтауға болады. 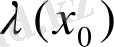<0 бұл реализация шексіздікте бір реализация шешімге жинақталады (уақыт бойынша өзара корреляция бірге ұмтылады) . 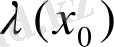>0 реализациялар ажырайды, қанша 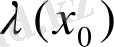көп болса реализация ажырауы жылдам болады.

Диссипативті динамикалық жүйе үшін Ляпунов көрсеткішінің қосындылары әрқашан да теріс.

Динамикалық хаосқа әрбір жеке траекториялар тұрақсыз жауап береді, сонымен қатар егер де Ляпунов көрсеткішінің ең болмағана бір оң көрсеткіші болса, онда бұл жағдайда аттракторды хаосты деп атайды.

Ляпунов көрсеткішінің көмегімен динамикалық жүйенің энтропиясын бағалай аламыз.

  1. Логистикалық бейнелеу генераторы

Логистикалық бейнелеу генераторын зерттейік [2- 4] .

\[\chi_{n+1}=Q\chi_{n}(|-\chi_{n})\]
. (1. 3)

Логистикалық бейнелеуді квадраттық бейнелеу деп те атайды, өзімен параболалық бейнелеуді нақты білдіреді [5] .

\[x_{n+1}=a\,+b x_{n}+\gamma x_{n}^{2}\]
. (1. 4)

\[a\,,b\,,\gamma\]
-басқарушы параметрлер.

\[(x)\]
-басқарушы параметр, енді
\[(x)\]
-параметрін өзгерткенде оның динамикасының қалай өзгеретінін қарастырайық.
\[\textstyle{\int_{a}}\]
-бейнелеуінің қозғалмайтын нүктелерін тауып аламыз, (
\[(x)\]
-индексін
\[\overline{{{\oint}}}\]
-ң
\[(x)\]
-параметріне тәуелділігін көрсетуі үшін қолданамыз) .

\[x_{e}=a\,x_{e}\,(1-x_{e}),a\]
>0. (1. 5)

Қозғалмайтын нүктелер:

\[x_{e}^{(1)}=0,\]
\[x_{e}^{(2)}={\frac{a-1}{a}}\]
. (1. 6)

Қозғалмайтын нүктелердің түрін анықтайық:

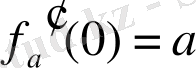. (1. 7)

\[f_{a}^{\phi}(\frac{a-1}{a})=2-a\]
. (1. 8)

(1. 7) мен (1. 8) теңдеулерін 1-ге теңестіре келе, қозғалмайтын нүктелер

\[{\ell}{\bar{\mathcal{A}}}\]
=1 және
\[{\ell}{\bar{\mathcal{A}}}\]
=3 мәндерінде тұрақтылығын жоғалтатынын байқадық. Тұрақтылығын жоғалту динамиканың сапалы өзгеруіне алып келеді, сонымен қатар
\[{\ell}{\bar{\mathcal{A}}}\]
=1 және
\[{\ell}{\bar{d}}\]
=3 периодты екі еселеу бифуркациясының орнына ие.

Логистикалық бейнелеу генераторында Ляпунов көрсеткішін пайдалана отырып r -айнымалы параметріне хаосты режимдегі мәнді таңдау керек, сонымен логистикалық бейнелеу генераторында r

\[\mathbf{\hat{\Pi}}\]
3, 56 деп аламыз және жүйеде тербелістің хаосты режимі байқалады. Бейнелеу параметрінің мәні процесстің хаостылық деңгейін анықтайды және жүйеде бола алатын мүмкін болатын күй сандары.

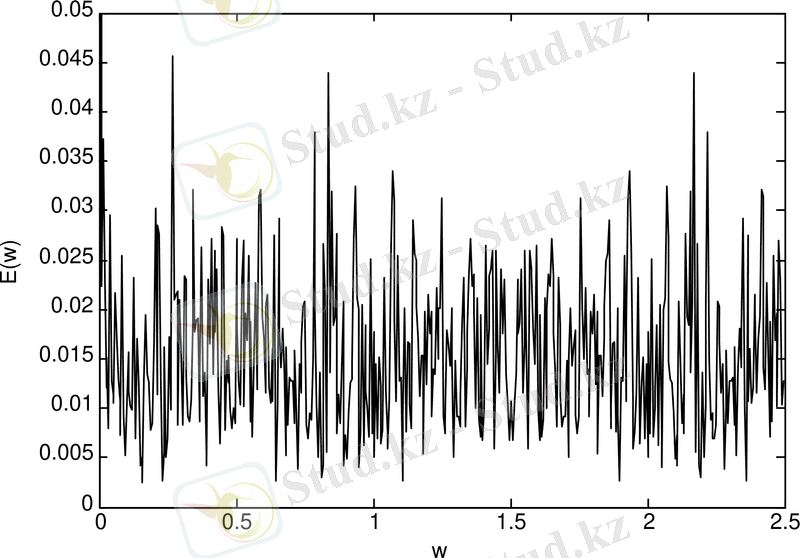
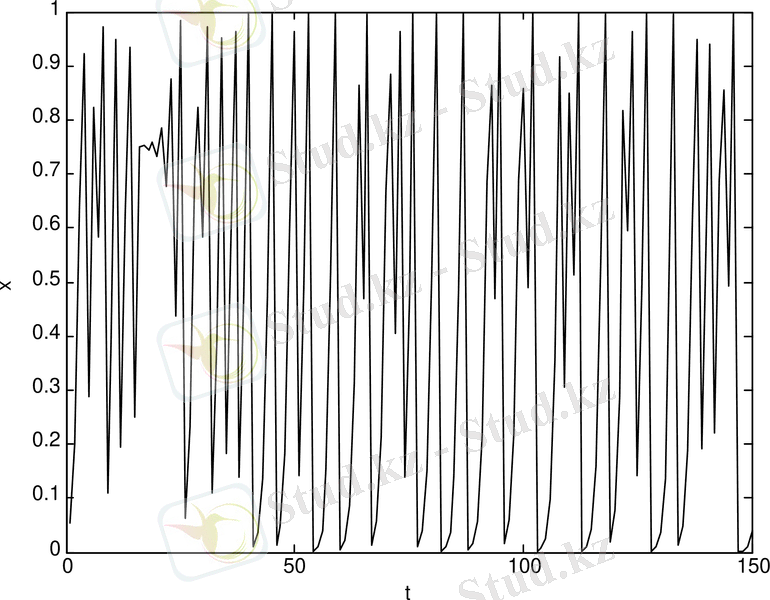
Логистикалық бейнелеу генераторының энергетикалық спектрі (сурет 1. 1-а) келтірілген. Логистикалық бейнелеу генераторының энергетикалық спектрі - біркелкі және кеңжолақты.

Процесс реализациясын сигнал деп те атайды. Логистикалық бейнелеу генераторының тербеліс реализациясы (сурет 1. 1-ә) көрсетілген.

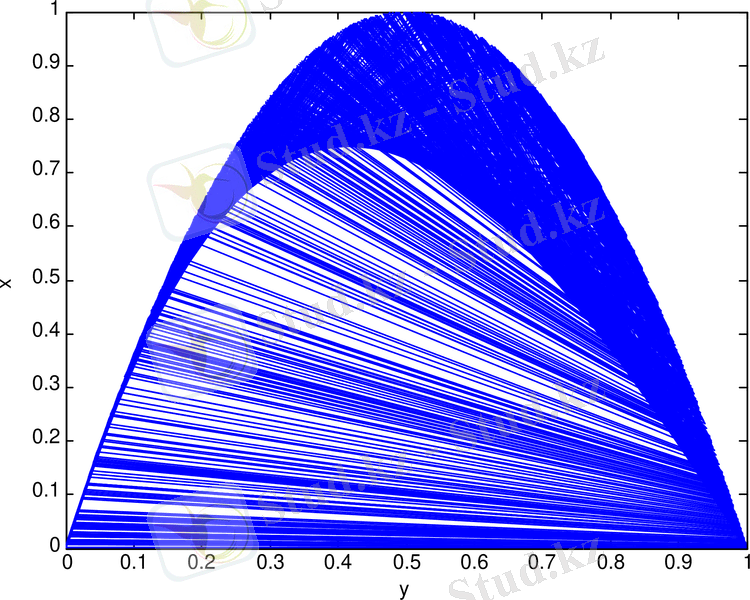
Логистикалық бейнелеу генераторының фазалық портретін (сурет 1. 1-б) көре аламыз.

а.

ә.

а.:

б.

Cурет 1. 1. Логистикалық бейнелеу генераторының: спектрі (а) ; тербеліс реализациясы (ә) ; фазалық портреті

Реализацияның (cурет 1. 1-а) ұзыңдығының үлкен емес мәндерінде спектр бастапқы шартқа тәуелді. Реализацияның үлкен бастапқы шарттың өзгерулерінің өзінде де спектр түріне аз әсер етеді. Сипаттамалары параметрге тәуелсіз түрде сақталады. Сигнал энергиясының аз бөлігі жоғарғы жиілікті аймақтарға негізделген.

Байланыс жүйесінде энергетикалық спектрдің бастапқы шартқа тәуелділігі қажетсіз, сондықтан хаосты сигнал реализациясының ұзындығын қолданған жөн.

  1. Хенон бейнелеу генераторы

Түзу жазықтықтағы екі өлшемді жағдай үшін квадраттық бейнелеуді қорытындылауды француз астрономы Хенон ұсынды [2] :

\[x_{n+1}=1-\ a x_{n}^{2}+y_{n}\]
,

\[y_{n+1}=J x x_{n}\]
. (1. 9)

a және b -басқарушы параметрлер.

Хенон бейнелеу генераторы - біртүрлі аттракторы бар динамикалық жүйенің абстрактілік мысалы ретінде 1976 жылы ұсынылған. Хенон бейнелеу генераторының теңдеуі (1. 9) -формулада көрсетілген. Біз қазір мұндай импульстік соғу әсерінен тұтқыр ортада, бөлшектердің қарапайым физикалық жүйелердің, оның қарқындылығы бірқатар координаттарына тәуелді болатын, динамикасын сипаттау үшін пайдаланылуы мүмкін екенін білеміз. Физикалық тұрғыдан қарайтын болсақ, шынайы болып b параметрінің оң мәндері табылады. Жазықтықтағы параметрлердің әртүстілігі периодтық режимдерді білдіреді. Сұр- хаос, ақ- шексіздікке ұмтылатын траектория бақыланатын аймақ (сурет 1. 2-в) .

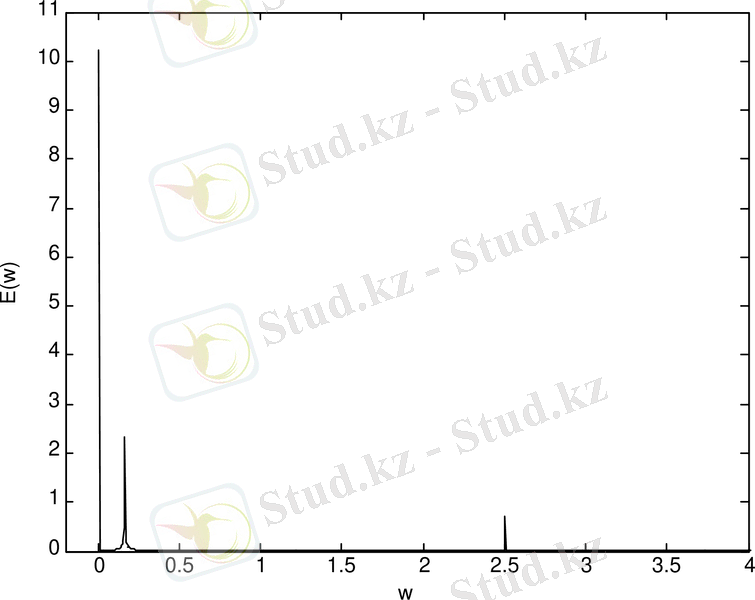
Хенон бейнелеу генераторының сигналының спектрі (сурет 1. 2-а) көрсетіледі. Спектрге қарап қарастырылған тербеліс хаосты екенін байқаймыз. Хенон бейнелеу генераторының спектрінде гармоникалар бар екені байқалып тұр.

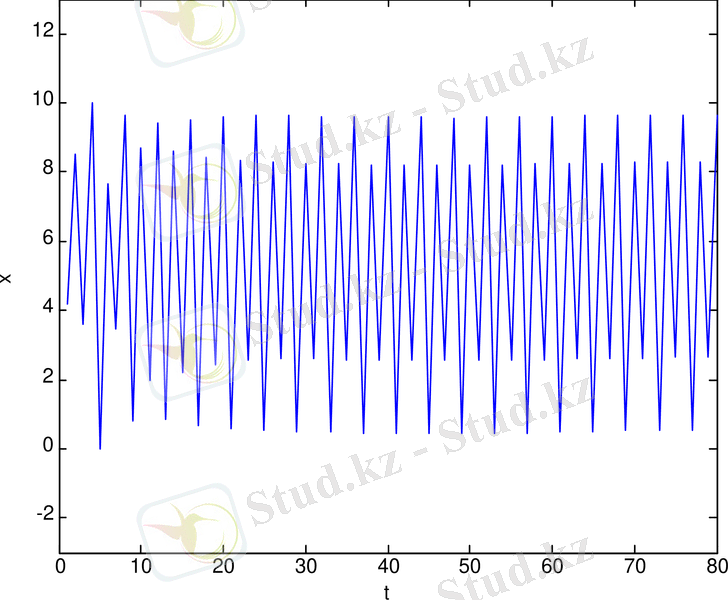
Хенон бейнелеу генераторының a =1. 3 және b =0. 4 мәндеріндегі тербеліс реализациясы (сурет 1. 2-ә) келтірілген.

Тербелістің a =1. 3 және b =0. 4 мәндеріндегі фазалық портреті (сурет 1. 2-б) көрсетілген [6, 7] .

а.

ә.

а.:

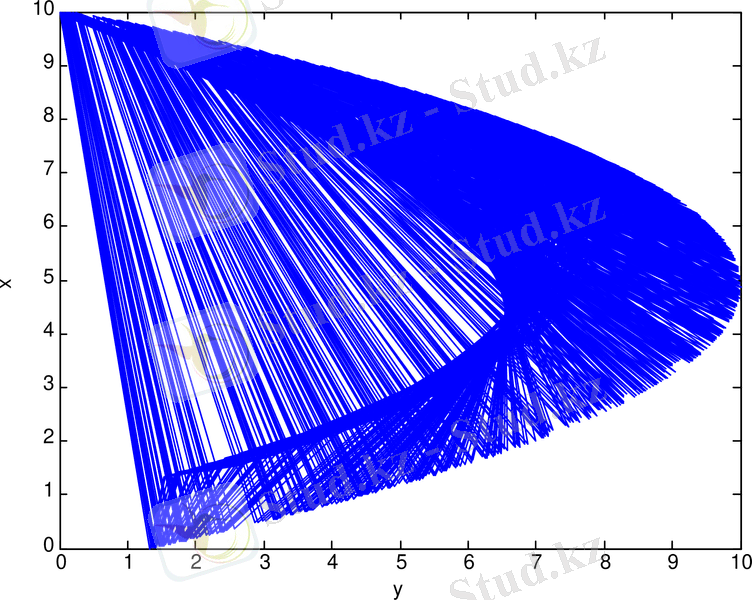
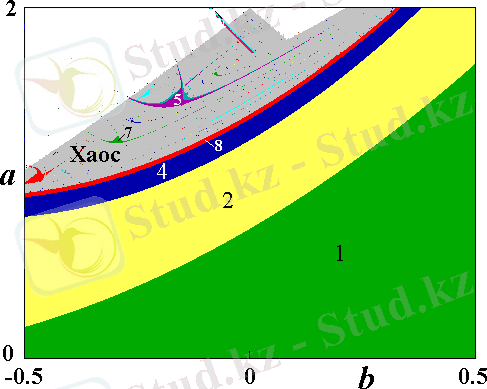
http://www.sgtnd.narod.ru/science/atlas/fig/hen_pln.gif

б. в.

Cурет 1. 2. Хенон бейнелеу генераторының: спектрі (а) ; тербеліс реализациясы (ә) ; фазалық портреті (б) ; бифуркациялық диаграммасы (в)

Сандық есептеулер көрсетіп тұрғандай жүйенің күйі Хенон аттракторының күрделі түрінің әртүлігіне қоюланады. Бұл аттрактор көптеген канторова құрылымына және геометриялық (көлемді) инвариантқа ие.

  1. Жинақталу және лақтыру генераторы

Кейбір функция модульдерінің уақыт бойынша эволюциясын қарастырақ x(t) -фракталды өлшемге байланысты [8] :

\[\frac{d x(t)}{d t}=s i g n(\frac{d x(t)}{d t})\frac{~\left|\mathrm{D}x\right|}{\left|\Delta t\right|^{1-p_{0}}}\]
. (1. 10)

\[\gamma_{0}\]
-t-ң көп мәндерінің статистикалық сипаттамасы, ол Лифшица -Гельдердің шартын қамтамасыз ету мақсатында
\[{\frac{d x}{d t}}\]
туындысын шектеу үшін енгізілген. Салыстырмалы модуль қадамы
\[\left|\Delta x\right|\]
фракталды өлшемділік шартының орнын басамыз
\[{\boldsymbol{x}}(t)\]
:

\[x=x_{0}(|\Delta x|)^{-(D-d)}\]
,
\[|\mathrm{D}x|={\hat{\aleph}}_{\left\langle{\mathbf{}\mathbf{\beta}}\right|}^{\mathrm{d}}|x_{0}\langle{\frac{-1}{\mathfrak{\lambda}}}^{\mathrm{cl}}\]
,
\[\gamma=D~{\mathrm{-}}d\]
(1. 11)

\[{\mathcal{X}}_{0}\]
-фракталды емес тұрақты өлшем,
\[{\boldsymbol{D}}\]
-
\[{\boldsymbol{x}}(t)\]
-ң көптеген мәндерінің фракталды өлшемі, d -шара тасушысының өлшемділік топологиясы. (1. 11) -формуланы (1. 10) -формулаға қоямыз дискретті айырымдарға өтеміз.
\[\mathrm{D}t>0\]
осыған байланысты арқашан sign(
\[\frac{\mathrm{D}x_{i}}{\Delta x_{i+1}}\]
d x i + 1 d x i \frac{dx_{i + 1}}{dx_{i}} ) -функция белгісі тек
\[\Delta x_{i}\]
-ге тәуелді. Оның дискретті айнымалы i бойынша өзгеруі мына түрде

\[\mu_{i}={\frac{\mathrm{D}x_{i}}{\Delta x_{i+1}}}{\big|}_{x_{i}=x_{i+1}}\]
.
\[\mu_{i+1}={\frac{\mathrm{{Dx}}_{i+1}}{\mathrm{{Dx}}_{i}}}{\Big|}_{x=x_{i+1}}={\frac{d x_{i+1}}{d x_{i}}}\]
(1. 12)

қозғалыссыз нүктеде жазылған. Негізінен

\[\mu_{i\cdot1}=\pm1\]
бұл мән сызықтық наразылық эволюциясын сипаттау үшін қолданылады. Біз
\[\textstyle{\mathcal{M}}_{i+1}\]
-ді
\[\textstyle\bigwedge\underline{{{\theta}}}\]
-арқылы анықтаймыз және бұл модуль өлшеміне шектеулер қоймаймыз. (1. 11), (1. 12) -формулаларды ескере отырып (1. 10) - формуланы
\[x_{0}=1\]
-үшін мына түрде жазамыз:

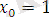
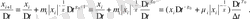(1. 13)

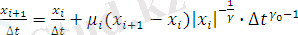
(1. 13) - формулада, уақыттың бірдей сәттерін таңдау үшін,

\[\gamma_{0}\]
-өлшемін алып тастаймыз.
\[\scriptstyle{1/2=1}\]
алгоритм дискретті есептеуге түсуден алдын,
\[x_{i}\Delta t^{-\gamma_{0}}\]
-өрнегін
\[\gamma_{0}\]
-өрнегі арқылы өзгертеміз, дәл осы өрнек,
\[x_{i}\Delta t^{\gamma_{0}}\]
-бұл емес, кездейсоқ мәндерге сәйкес
\[{\mathcal{X}}_{i}\]
.

\[\gamma_{0}\]
-өлшемін енгізу мағынасы шарттың жүзеге асуы болып табылуын ескеруіміз керек

\[{\frac{\mathbf{D}\mathbf{s}_{i}}{x_{i}}}({\frac{\mathbf{D}t}{T}})^{\gamma_{0}}=c o n s t\ \equiv c\]
(1. 14)

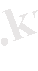
τ-процесске тән уақыт.

\[\gamma_{0}=0\]
-болған жағдайда
\[\mathrm{D}\mathbf{x}=c o n s t\]
-бойынша Риман өлшемін есептеуге ие болатын едік
\[\scriptstyle{1/2=1}\]
-болған кезде.
\[\gamma_{0}\ \neq0\]
-болған кезде Лебег өлшемін есептей аламыз,
\[\Delta t^{r_{0}}\]
-ң
\[\Delta x_{i}(y,x_{i})\]
-функция қадамына тәуелділігін ескере отырып:

\[(\frac{\mathrm{D}}{t})^{-s_{0}}=\frac{1}{c}\frac{\mathrm{D}x_{i}(\gamma,x_{i})}{x_{i}}=\frac{(|x_{i}|)^{-1/\gamma}}{c x_{i}}\]
. (1. 15)

\[{\mathcal{C}}^{\circ}\]
-тұрақты,
\[{\mathcal{C}}^{\circ}\]
-мағынасын сигналдың аналогтық базасы (күрделілігі) ретінде түсіндіруге болады, спектр сипаттамалары үшін қолданылады.

\[B=t_{k}\Delta\omega\]
. (1. 16)

\[\textstyle T_{k}\]
-корреляция уақыты,
\[\Delta o\]
-жиіліктің өткізу жолағы. (1. 14) -сипаттамаға сәйкес
\[{\mathcal{C}}^{\circ}\]
-хаосты сигналдың таңдалған анықтаулардың дәлдігінің үрделілігін сипаттайды. Фракталды нысан өлшемі бақылау дәлдігіне байланысты, сондықтан теория нәтижесіне
\[{\mathcal{C}}^{\circ}\]
-тұрақты кіреді. c c -мәні байқау процессінің дәлдік дәрежесін таңдауға сәйкес келеді:
\[c=10^{-2},\ \ 10^{-3}\]
.

\[\mathrm{D}t=\tau\]
-деп қарастырып (1. 13) - теңдеуді нақты мына түрде жазамыз:

\[x_{i+1}=(\frac{1}{c}+\mu_{i})|x_{i}|^{-\frac{1}{\gamma}}\nonumber\]
. (1. 17)

(1. 17) -формуланы дифференциалдап:

\[m_{i+1}={\frac{\mathrm{D}x_{i+1}}{\Omega x_{i}}}x_{i}=x_{i+1}=\cdot{\frac{1}{g}}({\frac{1}{c}}+m_{i})\vert x_{i}\vert^{-}{\frac{1}{\gamma}}-1\]
. (1. 18)

(1. 17) және (1. 18) -формулалары жинақталу және лақтыру генераторының [17] теңдеулері болып табылады.

Жинақталу және лақтыру генераторының спектрі (сурет 1. 3-а) ал тербеліс реализациясы (сурет 1. 3-ә) қарастырылған.

Жинақталу және лақтыру генераторының фазалық портреті (сурет 1. 3-б) көрсетілген.

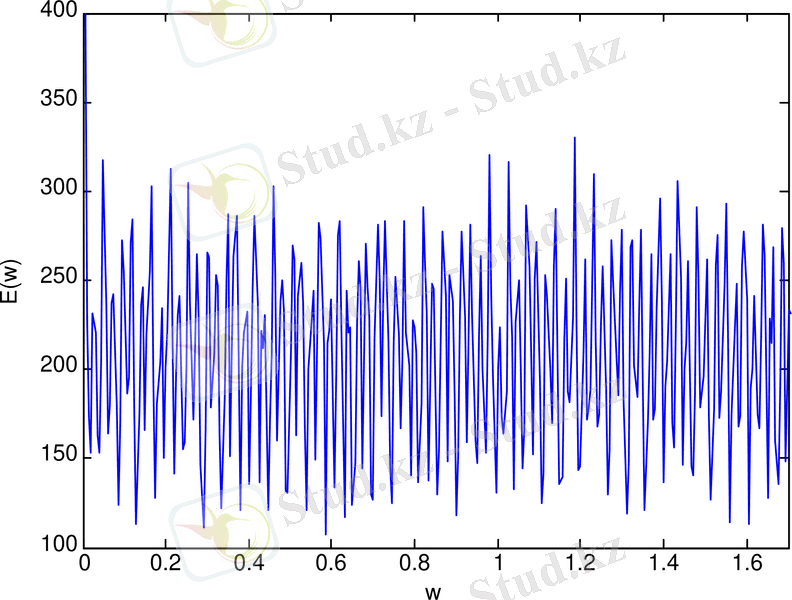
а.

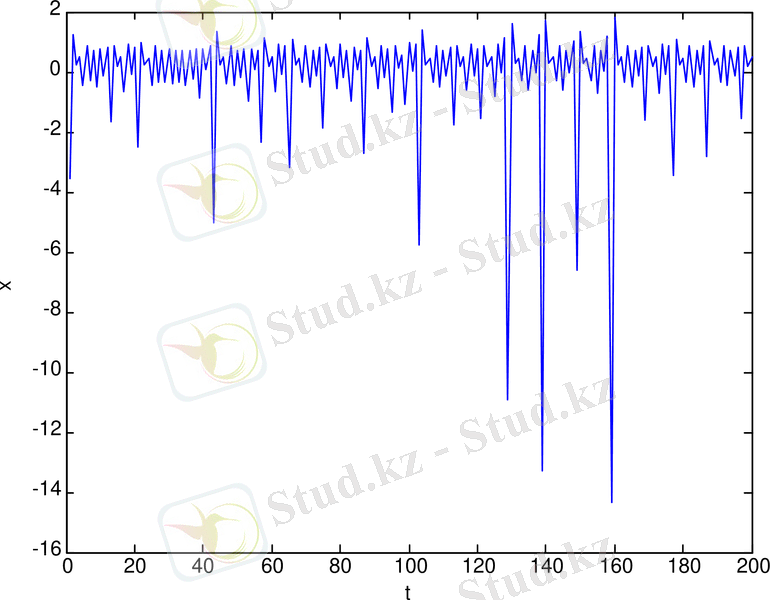
ә.

а.:

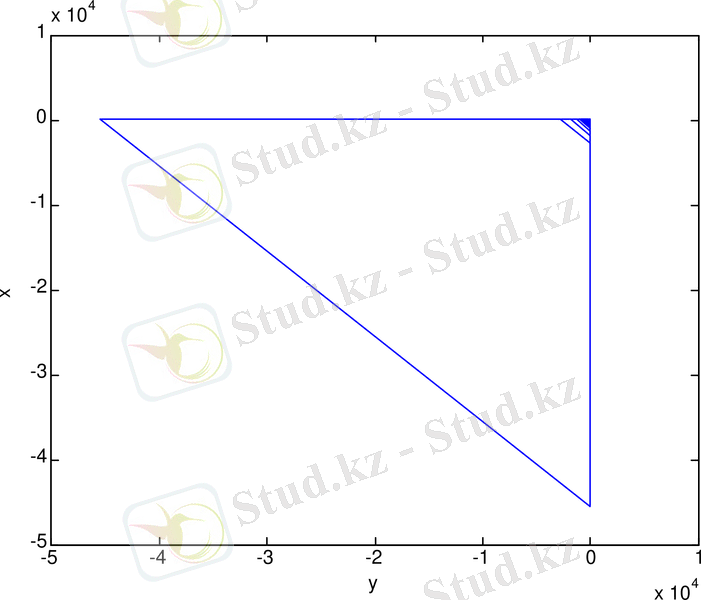
б.

Cурет 1. 2. Жинақталу және лақтыру генераторының: спектрі (а) ; тербеліс реализациясы (ә) ; фазалық портреті (б)

  1. Чуа генераторы

1983 жылы Леон Чуа хаосты тербелістерді көрсету үшін электронды схема ұсынған, бұл схема (сурет 1. 3) көрсетілген. Қазіргі таңда ол- радиоэлектроникада хаосты автогенераторлардың классикалық үлгісі болып табылады [9 - 13] .

\[{\frac{d x}{d t}}=a(y-\ x-h(x))\]
,
\[{\frac{d y}{d t}}=x-\ y+z\]
,
\[{\frac{d z}{d t}}=-\beta y\]
,

\[h(x)=m_{1}x+{\frac{1}{2}}(m_{0}-m_{1})(\left|x+1\right|-\left|x-1\right|)\]
(1. 19)

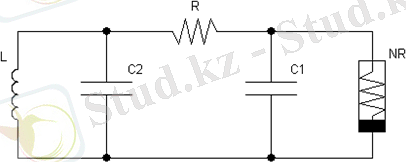
Сурет 1. 3. Чуа генераторының сұлбасы

\[{\frac{\vert V_{c1}}{\vert t}}={\frac{1}{c_{1}}}[{\frac{1}{R}}(V_{c2}\cdot\,V_{c1})-i_{M R}(V_{1})]\]
,

\[{\frac{\P V_{c2}}{\P t}}={\frac{1}{c_{2}}}[{\frac{1}{R}}(V_{c1}-V_{c2})-i_{L}]\]
,

\[{\frac{\P[i_{L}}{\P[t}}=-{\frac{1}{L}}V_{c2}\]
. (1. 20)

Чуа тізбегі - хаосты сигналдарды түрлендіре алатын алғашқы электр тізбегі. Тізбектің теңдеулері (1. 20) -формулада келтірілген. Тізбектің ерекшелігі оның қарапайым құрылымында болды. Тізбек төрт сызықты элементтен тұрды: екі конденсатор, бір индуктивтілік және кедергіден, сонымен қатар құрамында бейсызық активті элемент болды, бұл элементі қазіргі таңда Чуа диоды деп те атайды. Тізбек генераторды сипаттайды және Чуа диоды хаосты тербелістерге қол жеткізуде керек бөлік болып табылады.

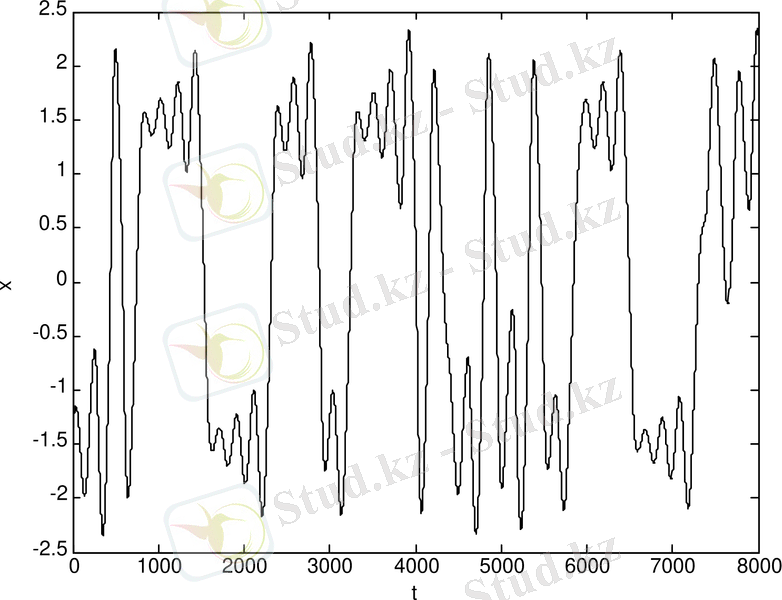
Чуа генераторының спектрі (сурет 1. 4-а) және екі спиральді аттрактор кезіндегі хаосты процесстің уақыттық реализация (сурет 1. 4-ә) келтірілген.

Чуа генераторының фазалық портреті (сурет 1. 4-б) көрсетілген.

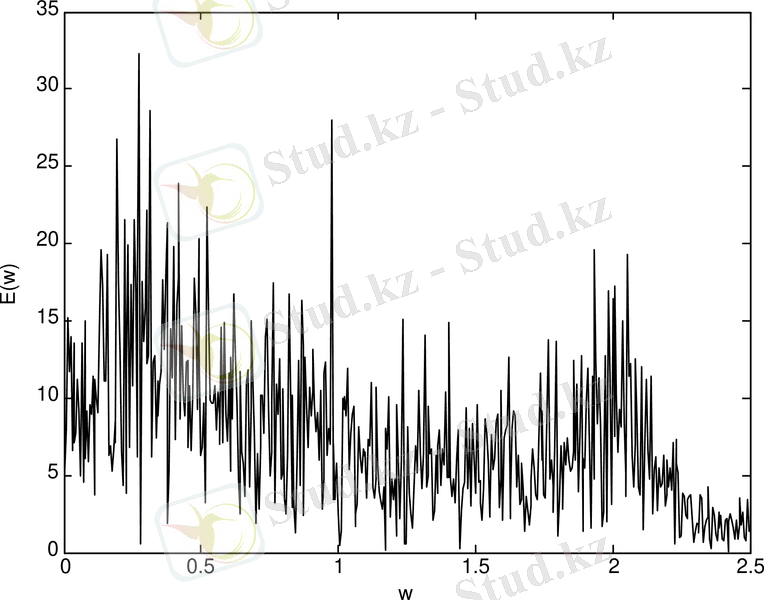
а.

ә.

а.:

б.

Cурет 1. 4. Чуа генераторының: спектрі (а) ; тербеліс реализациясы (ә) ; фазалық портреті (б)

Егер де сигналдың спектріне (сурет 1. 4-а) қарасақ, онда хаосты режим кезінде түрлендіру жолағы кең және ешқандай жарқын бейнеленген пиктер жоқ, сонымен қатар тұрақты құраушысынан басталады. Чуа генераторының спектрі дыбыстық диапазонда жатады.

Фазалық портретте (сурет 1. 4-б) Чуа генераторының хаосты екі спиральді аттракторы көрсетілген. Фазалық портретті бақылаған кезде байқайтынымыз: бірінші, шеңбер пайда болады, сосын осы тұрақты шеңбер екі ілмекті аттракторға айналады, ол хаостың басталғанын білдіреді. Бұл аттрактор тұрақтылықта үш нүктеге ие: бірі координатаның басында және екеуі ілмектің тесіктерінде. Аттрактордың траекториясы тесіктің бірінің айналасында айналудан басталады да, әрбір орамының тұрақтылық нүктесінен жойылып отырады, сосын траектория центрге қарай оралады және қайта жойылады немесе тұрақтылықтың басқа нүктесіне бағытталады. Айналу саны әр жағдайда кездейсоқ болады.

  1. Ван-дер-Поль генераторы

Автономды емес сыртқы гармоникалық әрекетті Ван-дер-Поль генераторы келесі дифференциалды теңдеумен сипатталады [14-16] .

\[\frac{d^{2}x}{d t}-\,m(1-\,l\,x^{2})\frac{d x}{d t}+w_{0}^{2}=B\cos\omega t\]
(1. 21)

Бұл дифференциалдық теңдеуді (1. 21) -формуланы Ван-дер-Поль теңдеуі деп те атайды, бұл теңдеу тербелістердің сызықсыз теориясының эталонды моделі болып табылады. Ол сызықсыз үйкелісті тербелмелі жүйені сипаттайды, үлкен тербеліс амплитудасында энергия шашырайды

\[{\mathcal{N}}\]
>
\[1/\lambda\]
және аз амплитудада жинақталады. Бұндай жүйелерге шекті циклдардың болуы тән; олар жақын ауытқиды, жылы ағын мен диссипация энергиясы теңгерілген, ғылым мен техниканың көптеген мәселелерінде орын алады.

Екінші ретті сызықсыз автономды емес дифференциалды теңдеу - бұл өлшемі жағынан ең аз хаосты тербелістер қозғалысы болуы мүмкін жүйе. Көптеген зерттеушілер

\[m,l\ ,\omega_{0}\]
, амплитуданы
\[{\underline{{\mathcal{A}}}}\]
, сыртқы әрекет етуші жиілікті
\[({\mathfrak{g}})\]
және хаосты тербелістерді автономды емес Ван-дер-Поль генераторында генерациялайтын параметрлерді анықтауға тырысты.

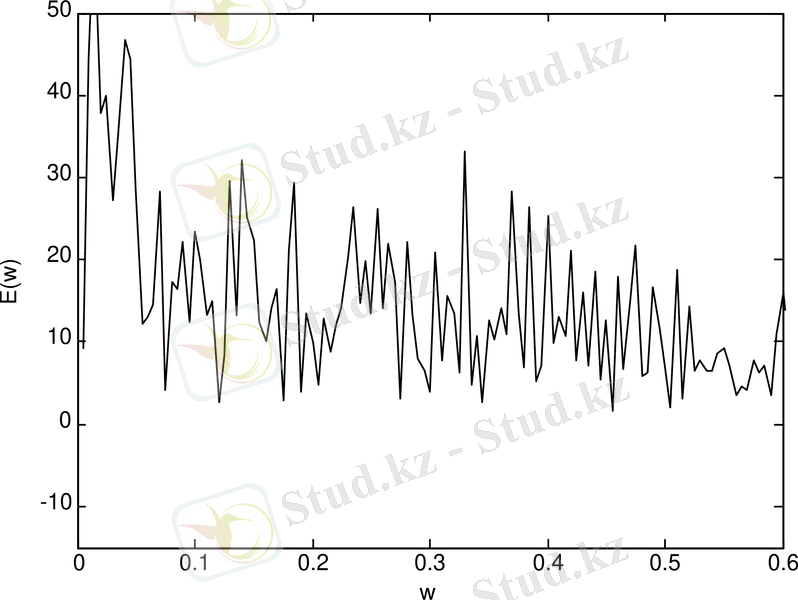
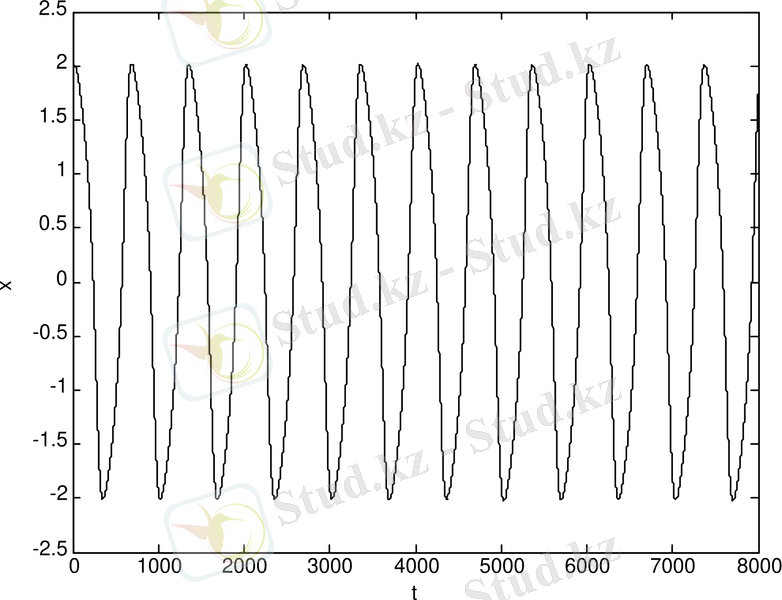
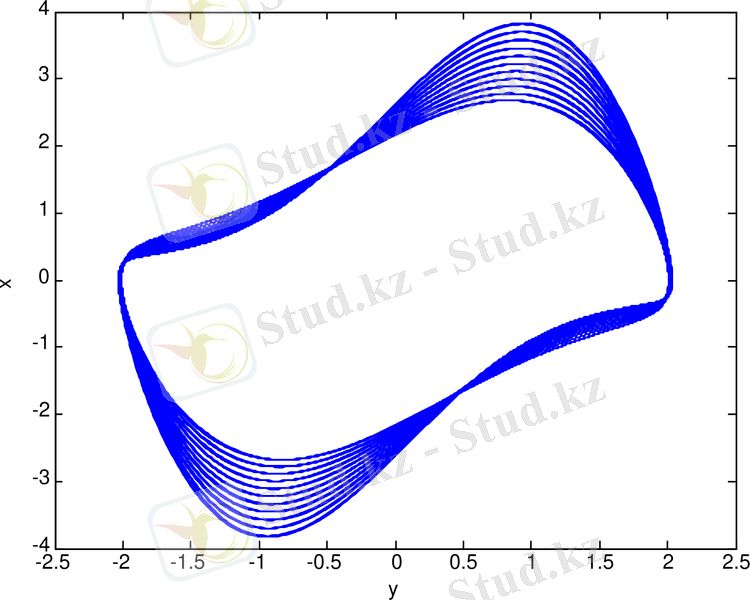
Ван-дер-Поль генераторының спектрі (сурет 1. 5-а) бейнеленген. Тербеліс спектрі айқын бейнеленген максимумдар сипаттамасына ие. Ван-дер-Поль генераторының тербеліс реализациясы (сурет 1. 5-ә) және фазалық портреті (сурет 1. 5-б) келтірілген.

а.

ә.

а.:

б.

Cурет 1. 5. Ван-дер-Поль генераторының: спектрі (а) ; тербеліс реализациясы (ә) ; фазалық портреті (б)

  1. Лоренц генераторы
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Хаостық генераторлар және олардың қолданыс аясы
Радиотехникалық динамикалық хаос генераторларының энергетикалық тиімділігін анықтау
Хаос генераторлары
Ганн диодтарындағы АЖЖ - құрылғылардың параметрлік сипаттамалары
Автоматты басқару және ақпараттар теориясынан мәліметтер
Генераторлар негізіндегі телекоммуникациялық жүйелер
Электр энергиясын генерациялау (өндіру)
ӨЛШЕУІШ ГЕНЕРАТОРЛАР
Радиотехникалық жүйелер
Электр машинасының есептеулері
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz