Электрондардың дифракциясы

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Семей қаласындағы Шәкәрім атындағы мемлекеттік университеті

Тақырыбы: Электрондардың дифракциясы

Орындаған: Қалиханова Әсел

Семей 2015

Электрондардың дифракциясы / electron diffraction - бастапқы шоқтардан белгілі бір бұрышқа ауытқыған қосымша электрондардың шоғы пайда болатын, электрондардың кристалдардан немесе сұйықтар мен газ молекулаларынан серпімді шашырауы.

Жарықтың толқындық қасиетімен қатар корпускулдық қасиеті болатыны белгілі. Жарықтың таралу кезінде (интерференция, дифракция) толқындық қасиеті байқалады, ал жарық заттармен әрекеттескенде (фотоэффект, атомдардың жарықты жұтуы және шығаруы) корпускулдық қасиеті байқалады. Фотонның бөлшек (энергиясы Е мен импульсі Р) ретінде толқындық қасиеті (жиілігі ν мен толқын ұзындығы λ ) арасында келесі қатынастар бар

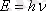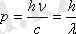, , мұндағы h=6, 63·10 ^-34 Дж·c - Планк тұрақтысы.

Франсуз физигі Луи де Бройль в 1924 ж. толқындық қасиет пен корпускулдық қасиет тек жарыққа ғана тән емес, бұл қасиеттер материалдық денелер үшін де тән деген болжам айтты. Оның болжамы бойынша v жылдамдықпен қозғалған массасы m денеге толқын ұзындығы 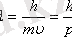қатынсымен анықталатын толқындық процесс сәйкес келеді. Толқындық қасиеттер әсіресе массалары өте аз элементар бөлшектерде айқын байқалады. Үйткені олардағы толқын ұзындығы атомдардың кристалдық торының өлшемдеріне сәйкес болады. Бұл жағдайда бөлшектер шоғының кристалдық тормен әрекеттесуі кезінде дифракция құбылысы байқалады. Мысалы, энергиясы 150 эВ электронға λ≈10 ^-10 м. Толқын ұзындығы сәйкес келеді. Бұл ұзындық атомаралық қашықтықтай. Сондықтан электрондар шоғы кристалда толқынға ұқсас шашырайды, яғни дифракция заңына сәйкес келеді. Электрондардың кристалда шашырауының моделі ретінде ой тәжірибесіндегі электрондардың бірөлшемді торда дифракциялануы деп қарастыруға болады. Толқындық көзқараста бұл ой тәжірибесі оптикадағы дифракциялық тордағы тәжірибеге толық эквивалентті. Фотопленкадағы дифракциялық сурет (электронограмма) кристалдық тордың үшөлшемді болатыны туралы ақпарат береді. Негізгі дифракциялық максимумдардың пайда болу орны тор формуласымен анықталады 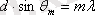, мұндағы d - тор периоды, 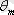- угол дифракция бұрышы, m- бүтін сан (порядок дифракциялық максимумның рет саны), λ-де Бройль толқын ұзындығы. Диракциялық бұрыш аз жағдайда 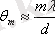. Егер фотопластинканы тордан белгілі бір L қашықтықта ораластырсақ, онда пластинада ені жіңішке дифракциялық жолақтар көрінеді. Олардың орны (дифракция бұрышы аз жағдайда) 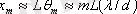формуласымен анықталады.

Кванттық физикада дифракциялық суреттердің интенсивтілігінің таралуы электрондардың экран нүктелеріне түсу ықтималдығының таралуы ретінде қарастырылады. Әр электрон тормен толқын ретінде әрекетеседі (яғни тор элементтерінің бәрімен толық әрекеттеседі), бірақ экранда ықтималдық процесс нәтижесі ретінде көрініс табады.

Дифракциялық тәжірибенің нәтижесі бойынша, ядроның өлшемі 10 ^{-15 м -дей болса,} ^{10-34 м толқын ұзындығын көру мүмкін емес екендігі белгілі. Ал микроскопиялық денелерге өтетін болсақ, мәселе басқаша. Мысалы, жылдамдығы 106} м/с және массасы m _э =9, 1∙10 ^-31 кг электрон үшін де-Бройль толқын ұзындығы м шамасында болады.

Де-Бройль болжамы 1927ж никель монокристалынан электрондардың шашырауын бақылаған К. Дэвиссон мен Л. Джермердің тәжірибелерінде

(10. 1-сурет) расталды.

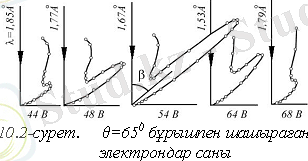
Электрондық зеңбірек электронды белгілі бір жылдамдықпен шығарып, никель монокристалына тиіп және одан электрондар шоғы шашырайды. Шашыраған электрондарды қабылдаушы ретінде Фарадей цилиндрі қолданылды, Фарадей цилиндріне түскен электрондар саны цилиндрдің электр тізбегіндегі ток күшіне пропорционал болған. Классикалық физика тұрғысынан электрондар мүмкін болатын бұрыштармен шашырауы керек. Бірақ та электрондардың -тан кіші бұрыштармен шашырауын бақылағанда, электр тізбегіндегі шашыраған электрондардың максимум саны (ток күшінің максимумы), энергиясы электронға (10. 2-сурет) тура келді, ол 0, 167 нм де-Бройль толқын ұзындығына сәйкес келеді. Электрондардың шашырауы.

Брэгга-Вульф шарты орындалған кездегі рентген сәулелерінің шашырауына ұқсас:

. (10. 4)

Сонымен, Дэвиссон мен Джермер тәжірибелері де-Бройльдың электрондарының толқындық қасиеті бар гипотезасын дәлелдеді. Кейінірек электрондардың толқындық қасиеті басқа да тәуелсіз тәжірибелермен дәлелденді. Де Бройль толқындарының кейбір қасиеттерін қарастырайық. Де Бройль толқынының фазалық жылдамдығын есептейік. Кез- келген толқынның фазалық жылдамдығы мынаған тең:

, (10. 5)

мұндағы - толқындық вектор, оның модулі -ға тең. Түрлендіруден кейін

, (10. 6)

болғандықтан, де-Бройль толқынының фазалық жылдамдығы вакуумдағы жарық жылдамдығынан артық болуы мүмкін. Де-Бройль толқынының топтық жылдамдығын мына формула бойынша есептейміз

. (10. 7)

Еркін бөлшектер үшін , олай болса

(10. 8)

Соңғы өрнектен, де-Бройль толқынының топтық жылдамдығы бөлшектің өзінің жылдамдығына тең. Бұл де Бройль толқындары ерекше табиғатқа ие және оларды кеңістікте уақыт бойынша жайылатын толқындық пакет ретінде қарастыруға болмайтынына қажетті дәлелдеме болды. Топтық жылдамдық үшін өрнекті түрлендірейік

. (10. 9)

Де-Бройль толқынының топтық жылдамдығы бөлшектің өзінің жылдамдығына тең екенін ескерсек, онда:

. (10. 10)

Соңғы өрнекті интегралдап, мынаны аламыз:

. (10. 11)

Соңғы теңдеу де-Бройль толқынына сәйкес келетін жиілік пен еркін бөлшектің энергиясының байланысын өрнектейді. Кристалдардағы электрондардың шашырауы бойынша жүргізілген тәжірбиелерде, жоғарыда көрсетілгендей басқа барлық бағыттарға қарағанда жеке бағыттарды электрондардың үлкен санының шашырайтындығы байқалады. Толқындық көзқарасынан қарағанда, кейбір бағыттарда электрондардың максимум санының болуы, бұл бағыттарда де-Бройль толқынының үлкен интенсивтігі бар екенін білдіреді. Толқын интенсивтігі тоқын амплитудасының квадратына пропорционал болатындығын есепке ала отырып, де-Бройль толқынына өздігінше ықтималды талқылама беруге болады. Кеңістіктің берілген көлеміндегі де-Бройль толқынының амплитуда модулының квадраты , бөлшектің осы көлемде бар болу (немесе табылу) ықтималдығын білдіреді.

Берілген уақыт мезетінде тұрған бөлшектің ықтималдылығы орналасуын сипаттау үшін деп аталатын толқындық