Тейлор қатары, аналитикалық функциялардың жалғыздық теоремесі және алгебраның негізгі теоремесі


Тейлор қатары. Жалғыздық теоремасы
Лекция мақсаты: Аналитикалық функцияларды Тейлор қатарына
жіктеу әдісімен, алгебраның негізгі теоремасымен
және аналитикалық функцияның жалғыздық
теоремасымен танысу.
Лекция жоспары:
1. Аналитикалық функцияларды Тейлор қатарына жіктеу.
2. Алгебраның негізгі теоремасы.
Лекция мәтіні:
1. Аналитикалық функцияларды Тейлор қатарына жіктеу.
Теорема1: Аналитикалық функцияны облыстың әрбір ішкі нүктесінде жинақталу радиусы а нүктеден облыс шекарасына дейінгі ең қысқа қашықтықтан кем болмайтын Тейлор қатарына жіктеуге болады.
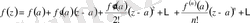 (1)
(1)
Функция
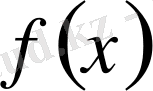 облыс
облыс
 - да аналитикалық,
- да аналитикалық,
 нүкте осы
нүкте осы
 облыстың кез келген ішкі нүктесі болсын.
облыстың кез келген ішкі нүктесі болсын.
 - дан облыс
- дан облыс
 - ның шекарасына дейінгі ең қысқа қашықтықты
- ның шекарасына дейінгі ең қысқа қашықтықты
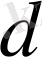 арқылы белгілейік. Центрі
арқылы белгілейік. Центрі
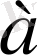 - нүктеде жатқан, радиусы
- нүктеде жатқан, радиусы
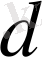 - ға тең шеңбер жүргіземіз және оның ішінде еркін бір нүкте
- ға тең шеңбер жүргіземіз және оның ішінде еркін бір нүкте
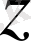 - ті аламыз. Содан соң
- ті аламыз. Содан соң
 нүктенің төңірегінде екінші шеңбер
нүктенің төңірегінде екінші шеңбер
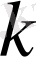 - ны сызамыз. Бұл шеңбердің
- ны сызамыз. Бұл шеңбердің
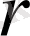 - ең қысқа қашықтық
- ең қысқа қашықтық
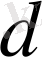 -
дан кіші. Алайда
-
дан кіші. Алайда
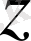 нүкте
нүкте
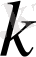 - ның ішінде жататындай жеткілікті үлкен. Функция
- ның ішінде жататындай жеткілікті үлкен. Функция
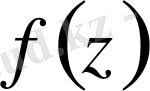
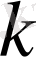 - ны өз ішіне алатын облыс
- ны өз ішіне алатын облыс
 -
да аналитикалық болғандықтан Кошидің интегралдық формуласына сәйкес
-
да аналитикалық болғандықтан Кошидің интегралдық формуласына сәйкес
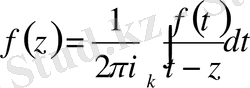 (2)
(2)
Интеграл астындағы бөлшекті
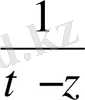 - ті мынадай түрлендіреміз.
- ті мынадай түрлендіреміз.
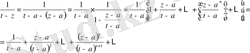
(3)
Нәтижеде геометриялық прогрессия алдық.
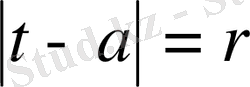 ,
,
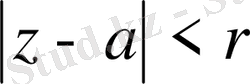 ,
,
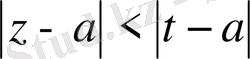
Демек,
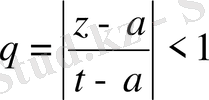 болғандықтан, жоғарыда алынған прогрессия жинақталады.
болғандықтан, жоғарыда алынған прогрессия жинақталады.
(3)
- тің екі жағын
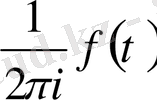 - ға көбейтіп, келесіні аламыз.
- ға көбейтіп, келесіні аламыз.
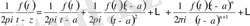 (4)
(4)
Егер интегралдау қисығында қатар бірқалыпты жинақталса, онда комплекс қатарлар үшін
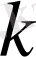 шеңберде
(4)
қатардың бірқалыпты жинақталатынын дәлелдеуге болады. Енді функцияның ерекше нүктелері белгілі болғанда, Тейлор қатарының жинақталу радиусын анықтайық. Бұл үшін келесі анықтаманы енгіземіз.
шеңберде
(4)
қатардың бірқалыпты жинақталатынын дәлелдеуге болады. Енді функцияның ерекше нүктелері белгілі болғанда, Тейлор қатарының жинақталу радиусын анықтайық. Бұл үшін келесі анықтаманы енгіземіз.
Анықтама:
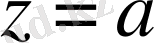 нүкте функцияның
регулярлы нүктесі
деп аталады, егер оның қандай да бір маңайында функция аналитикалық болса.
нүкте функцияның
регулярлы нүктесі
деп аталады, егер оның қандай да бір маңайында функция аналитикалық болса.
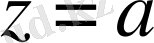 нүкте функцияның
ерекше нүктесі
деп аталады, егер функция аналитикалық болмаса.
нүкте функцияның
ерекше нүктесі
деп аталады, егер функция аналитикалық болмаса.
Егер функция
 облыста аналитикалық болса, онда облыстың әрбір ішкі нүктесі функцияның регулярлы нүктесі болады. Функцияның үзіліс нүктелері және тармақталу нүктелері ерекше нүктеге мысал бола алады.
облыста аналитикалық болса, онда облыстың әрбір ішкі нүктесі функцияның регулярлы нүктесі болады. Функцияның үзіліс нүктелері және тармақталу нүктелері ерекше нүктеге мысал бола алады.
Шынында да, үзіліс нүктелерінің және тармақталу нүктелерінің қандай да кіші маңайын алмайық, ол бұл нүктеде не функцияның , не бірмәнділігі бұзылады.
Мысалы:
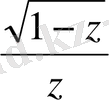 ,
,
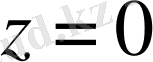 үзіліс нүктесі және
үзіліс нүктесі және
 тамақталу нүктесі. Осы нүктеден өзге ақырлы нүктелері регулярлы нүкте,
тамақталу нүктесі. Осы нүктеден өзге ақырлы нүктелері регулярлы нүкте,
 тармақталу нүкте болатынын оңай тексеруге болады.
тармақталу нүкте болатынын оңай тексеруге болады.
Егер функцияның ерекше нүктелері белгілі болса, онда оның
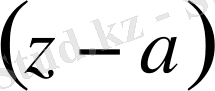 - ның дәрежелері бойынша жіктелуінің жинақталу радиусын былай табуға болады.
- ның дәрежелері бойынша жіктелуінің жинақталу радиусын былай табуға болады.
Функцияның ерекше нүктелері оның аналитикалығының облысы үшін шекаралы болады. Сондықтан алдыңғы теоремаға сәйкес Тейлор қатарының жинақталу радиусы
 нүктеден функцияның
нүктеден функцияның
 нүктеге жақын ерекше нүктеге дейінгі қашықтықтан кем емес. Алайда, жинақталу радиусы бұл қашықтықтан үлкен бола алмайды. (Үлкен болған жағдайда ерекше нүкте жинақталу дөңгелегінің ішіне түсіп қалады. )
нүктеге жақын ерекше нүктеге дейінгі қашықтықтан кем емес. Алайда, жинақталу радиусы бұл қашықтықтан үлкен бола алмайды. (Үлкен болған жағдайда ерекше нүкте жинақталу дөңгелегінің ішіне түсіп қалады. )
Алдыңғы лекциядағы теоремаға сәйкес дәрежелік қатардың қосындысы жинақталу дөңгелегінде аналитикалық. Сондықтан онда функцияның ерекше нүктесі болуы мүмкін емес. Сонымен біз келесі теореманы дәлелдедік.
Теорема 2 :
Функцияны
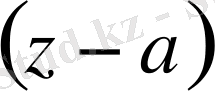 - ның дәрежесі бойынша Тейлор қатарына жіктеудің жинақталу радиусы нүктеден функцияның жақын жатқан ерекше нүктесіне дейінгі қашықтыққа тең.
- ның дәрежесі бойынша Тейлор қатарына жіктеудің жинақталу радиусы нүктеден функцияның жақын жатқан ерекше нүктесіне дейінгі қашықтыққа тең.
Мысалы:
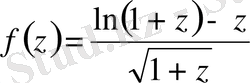 функцияны
функцияны
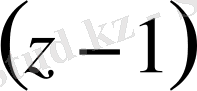 -дің дәрежесі бойынша жіктеудің алғашқы екі мүшесін және қатардың жинақталу радиусын табайық.
-дің дәрежесі бойынша жіктеудің алғашқы екі мүшесін және қатардың жинақталу радиусын табайық.
Шешуі:
Есептің шартына сәйкес біз мына қатарды алуымыз қажет:
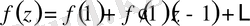
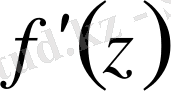 туындыны таба,
туындыны таба,
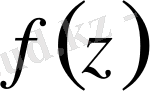 және
және
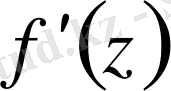 - де
- де
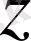 - тің орнына 1 санын қоя келесіні табамыз.
- тің орнына 1 санын қоя келесіні табамыз.
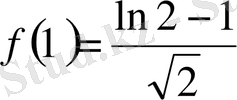
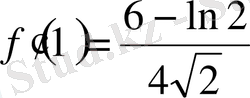
Демек, таппақшы болған жіктеуіміз келесіге тең:
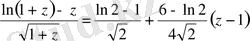
Қатардың жинақталу радиусын табу үшін функцияның ерекше нүктелерін анықтаймыз. Бұл үшін түбір астындағы өрнекті және логарифм белгісі астында тұрған өрнекті 0 -ге теңестіріп табамыз.
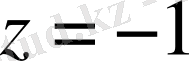 , тармақталудың алгебралық нүктесі.
, тармақталудың алгебралық нүктесі.
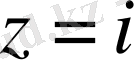 және
және
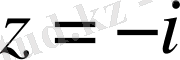 тармақталудың логарифмдік нүктесі.
тармақталудың логарифмдік нүктесі.
 нүктеден ерекше нүкте
нүктеден ерекше нүкте
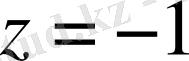 - ге дейінгі қашықтық 2 - ге тең, ал
- ге дейінгі қашықтық 2 - ге тең, ал
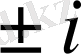 еркше нүктеге дейінгі қашықтық
еркше нүктеге дейінгі қашықтық
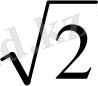 - ге тең. Бұл қашықтықтардың ең қысқасы
- ге тең. Бұл қашықтықтардың ең қысқасы
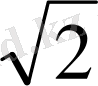 - ге тең. Демек, жинақталу радиусы
- ге тең. Демек, жинақталу радиусы
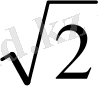 - ге тең. Қорытындыда келесі ескертпелерді келтірейік.
- ге тең. Қорытындыда келесі ескертпелерді келтірейік.
1.
Дәрежелі қатарға жіктеудің келесі жалғыздық қасиеті орынды. Егер
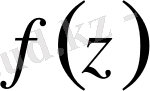 функция
функция
 нүктенің маңайында
нүктенің маңайында
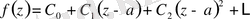
дәрежелік қатарға жіктелсе, онда қатар функцияның Тейлор қатары деп аталады. .
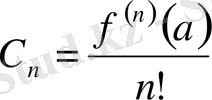
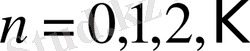
2. Теорема 1 комплексті айнымалы функцияның нақты айнымалы функцияның тағы да бір айырмашылығын (өзгешелігін) айқындап береді. Бұл теоремаға сәйкес, егер функция облыстың әрбір нүктесінде бірінші ретті туындыға ие болса, онда облыстың әрбір нүктесінде Тейлор қатарына жіктелуі мүмкін. Нақты облыста бұл олай емес.
3. Жоғарыда талқыланған Коши мысалы (кітаптан қара. ) нақты айнымалы функциялар теориясының түсіндіре алмаған сұрақтарды комплексті айнымалы функциялар теориясы түсіндіре алатындығын көрсетеді.
4. Математикалық анализ курсында берілген қатарды Тейлор қатарына жіктеуге болады және егер мүмкін болса, қатардың жинақталу радиусы неге тең деген сұраққа жауап беру өте қиын. Комплексті айнымалы функциялар теориясында бұл сұраққа жауап беру оңай, егер функция аналитикалық және оның ерекше нүктелері белгілі болса.
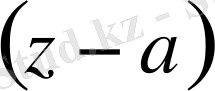 - ның дәрежелері бойынша жіктеу мүмкін, егер
- ның дәрежелері бойынша жіктеу мүмкін, егер
 функцияның регулярлы нүктесі болса, жинақталу нүктесі
функцияның регулярлы нүктесі болса, жинақталу нүктесі
 нүктеден жақын тұрған ерекше нүктеге дейінгі қашықтыққа тең болса.
нүктеден жақын тұрған ерекше нүктеге дейінгі қашықтыққа тең болса.
Тейлор қатарының коэффициенттеріне берілген Коши бағасы келесі теоремамен беріледі.
Теорема 3:
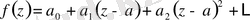 коэффициенттері үшін келесі бағалау орынды:
коэффициенттері үшін келесі бағалау орынды:
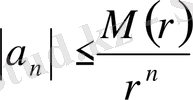 .
.
Мұнда,
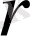 - қатардың жинақталу радиусынан кіші кез келген сан.
- қатардың жинақталу радиусынан кіші кез келген сан.
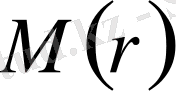 - радиусы
- радиусы
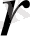 - ге тең
- ге тең
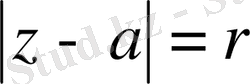 шеңберде функция модулінің максимумы.
шеңберде функция модулінің максимумы.
(Дәлелдеу үшін
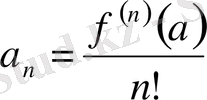 коэффициентін анықтайтын формуласын, өткен лекциядағы жоғарғы ретті туындыларды анықтау, сондай - ақ келесі теңсіздікті қолданамыз.
коэффициентін анықтайтын формуласын, өткен лекциядағы жоғарғы ретті туындыларды анықтау, сондай - ақ келесі теңсіздікті қолданамыз.
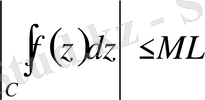 . Мұнда
. Мұнда
 - функция максимумы,
- функция максимумы,
 - қисықтың ұзындығы.
- қисықтың ұзындығы.
Теорема 4: (Лиувилл теоремасы)
Егер функция бүкіл жазықтықта аналитикалық және онда шектелген болса, онда
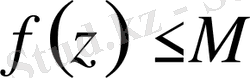 , онда функция тұрақтыға тең.
, онда функция тұрақтыға тең.
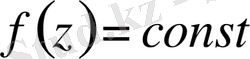
2. Алгебраның негізгі теоремасы.
Теорема 5:
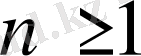 дәрежелі еркін комплексті коэффициентті алгебралық теңдеу
дәрежелі еркін комплексті коэффициентті алгебралық теңдеу
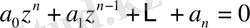
ең болмағанда бір түбірге ие.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz