Лаплас түрлендіруінің теориясы мен қасиеттері


Қазақстан Республикасының Білім және ғылым министрлігі
Семей қаласының Шәкәрім атындағы мемлекеттік университеті
СӨЖ
Тақырыбы: лаплас түрлендіру қасиеттері
Орындаған: Кусманов А.
Тексерген: Секербаева А. Б.
2015
Жоспары:
1. Лаплас түрлендіру.
2. Түпнұсқа және бейне. Лаплас интегралы.
3. Лаплас түрлендіруінің қасиеттері
- Лаплас түрлендіру.
Лаплас түрлендіру. Бұл өрнектер Фурье түрлендірумен тығыз байланысқан. Өңдеу теориясында Фурье түрлендіруі жоқ болатын бір неше функциялар бар, мысалы,
 немесе
немесе
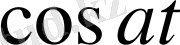 , себебі түрлендіруді белгілейтін интегралдың шешімі жоқ. Бірақ осындай функциялар да үшін спектрлік түрлендірудің аппараты құрастырылған.
, себебі түрлендіруді белгілейтін интегралдың шешімі жоқ. Бірақ осындай функциялар да үшін спектрлік түрлендірудің аппараты құрастырылған.
Әр түрлі геофизикалық процесті зерттегенде уақыт
 ден
ден
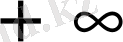 -ке дейін өзгереді деп санайды. Бірақ практикалық жағдайда процесс 0-ге тең деп алуға болатын белгілі бір уақыт мезгілінде басталады. Осылайша,
-ке дейін өзгереді деп санайды. Бірақ практикалық жағдайда процесс 0-ге тең деп алуға болатын белгілі бір уақыт мезгілінде басталады. Осылайша,
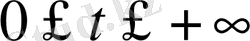 . Осындай жағдай болуы мүмкін, егер
. Осындай жағдай болуы мүмкін, егер
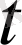 <0 болғанда
<0 болғанда
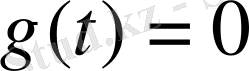 . Онда Фурье түрлендіру былай жазылады:
. Онда Фурье түрлендіру былай жазылады:
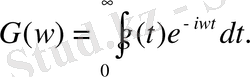 (1. 1)
(1. 1)
Интегралдың шешімі жоқ функциялардың Фурье түрлендіру есептеунің мүмкін еместігін аттап өтуге болады, егер Фурье түрлендірудегі
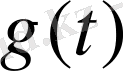 уақыттық функциясын
уақыттық функциясын
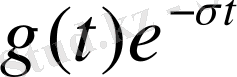 басылатын функциясына аустырсақ (мұндағы
басылатын функциясына аустырсақ (мұндағы
 -
-
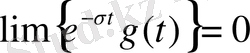 тең болатындай кез-келген нақты, оң және жоғары параметр) . Бұл жағдайда
тең болатындай кез-келген нақты, оң және жоғары параметр) . Бұл жағдайда
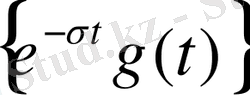 функциясының Фурье түрлендіруі болады, бірақ оны
функциясының Фурье түрлендіруі болады, бірақ оны
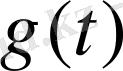 функциясынан Лаплас түрлендіруі деп атайды. Егер
функциясынан Лаплас түрлендіруі деп атайды. Егер
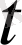 <0 болған жағдайда
<0 болған жағдайда
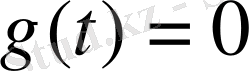 болса, онда біржақты Лаплас түрлендіруін аламыз:
болса, онда біржақты Лаплас түрлендіруін аламыз:
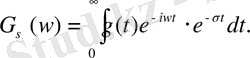
Бұл интегрдаың шешімі барлық жағдайларда болады, егер
 . Бұл формуланы келесі түрге келтірейк:
. Бұл формуланы келесі түрге келтірейк:
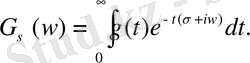
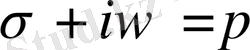 комплексті компонента пайда болғанын көріп отырмыз. Ауыстыруларды енгізейк:
комплексті компонента пайда болғанын көріп отырмыз. Ауыстыруларды енгізейк:
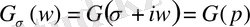 . Онда
. Онда
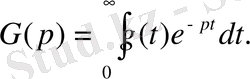 (1. 2)
(1. 2)
Бұл өрнекті түрлендіру ретінде қарастыруға болады. Оның көмегімен
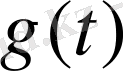 уақыттық функциясынан
уақыттық функциясынан
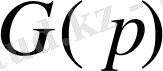 спектріне аусуға болады.
спектріне аусуға болады.
Физикалық түсіндіруден басқа Лаплас түрлендіруінің келесі түсініктемесін қосайық. Қалайша фотокамера оригиналдан кескінді алуға мүмкіндік береді, солайша Лаплас түрлендіруі
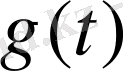 функция-оригиналдың
функция-оригиналдың
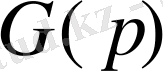 функция-кескінін анықтайды. Сонымен, Лаплас түрлендіруінің нақты мағынасы функцияны оригинал кеңістігінен кескін кеңістігіне ауыстыруда болып табылады және оригинал кеңістігімен салыстырғанда кескін кеңістігіндегі математикалық түрлендірулер бір неше қарапайым және көрнекті.
функция-кескінін анықтайды. Сонымен, Лаплас түрлендіруінің нақты мағынасы функцияны оригинал кеңістігінен кескін кеңістігіне ауыстыруда болып табылады және оригинал кеңістігімен салыстырғанда кескін кеңістігіндегі математикалық түрлендірулер бір неше қарапайым және көрнекті.
Лаплас түрлендіруінің сызықтылық қасиеттеріне, яғни аддитивтілік және біртектілік қасиеттеріне, ие болатынын дәлелдеп шығарайық.
Егер
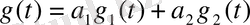 , онда
, онда
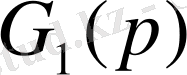 және
және
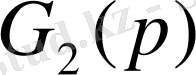 сәйкесінше
сәйкесінше
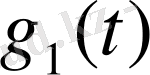 және
және
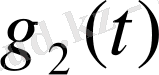 уақыттық функцияларының Лаплас спектрлері болып табылады.
уақыттық функцияларының Лаплас спектрлері болып табылады.
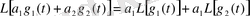 немесе
немесе
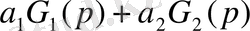 тең екендігін дәлелдеп шығарайық. Дәлелдеуі:
тең екендігін дәлелдеп шығарайық. Дәлелдеуі:
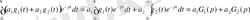 . (1. 3)
. (1. 3)
Лаплас түрлендіруінің дәнімен
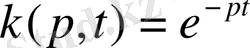 функциясы болады.
функциясы болады.
Мысал 1.
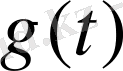 функциясы бірлік Хависайд функциясы болсын:
функциясы бірлік Хависайд функциясы болсын:
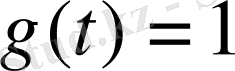 егер
егер
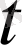 >0
>0
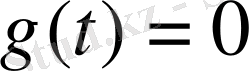 егер
егер
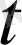 <0
<0
Лаплас түрлендіруін табамыз:
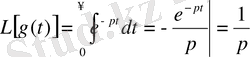 .
.
Фурье түрлендіруіне ұқсас, Лаплас түрлендіруі тура және кері болып табылады. Кері Лаплас түрлендіруі келесі өрнекпен сипатталанады:
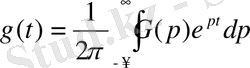 . (1. 4)
. (1. 4)
Егер біз жиілікке немесе фазаға тәуелді сигнал қасиеттерін зерттесек, онда Фурье түрлендіруін пайдалануға ыңғайлы болады. Оны ықтималдық теориясының белгілі бір бөліктерінде және Фурье немесе Фурье-Бессель қатарлар сияқты шекаралық шарттарымен сызықтық дифференциалды теңдеулерді шешкенде кең пайдаланады. Лаплас түрлендіруін пайдалануға ыңғайлы болады, егер түрлендірулердің аналитикалық қасиеттері зерттелінсе немесе алғашқы шарттары белгілі тұрақты коэффициенттерімен сызықтық дифференциалды теңдеулерді шешкенде.
2. Түпнұсқа және бейне. Лаплас интегралы.
Нақты айнымалы t-ның
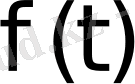 функциясы үшін мына шарттар орындалсын:
функциясы үшін мына шарттар орындалсын:
1) Айнымалы t-ның
 мәндерінде функция мәні
мәндерінде функция мәні
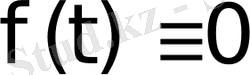 болсын;
болсын;
2) Нақты айнымалы t-ның
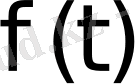 функциясы барлық
функциясы барлық
 мәндерінде үздіксіз болсын.
мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген
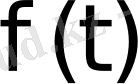 функциясының
функциясының
 өсу дәрежесі шектеулі болсын, яғни барлық
өсу дәрежесі шектеулі болсын, яғни барлық
 мәндерінде
мәндерінде
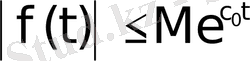 теңсіздігі орындалатындай
теңсіздігі орындалатындай
 және
және
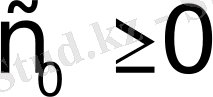 сандары табылсын. Осы шартты қанағаттандыратын
сандары табылсын. Осы шартты қанағаттандыратын
 сандарының ең кішісі
сандарының ең кішісі
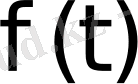 функциясының өсу көрсеткіші деп аталады.
функциясының өсу көрсеткіші деп аталады.
Осы (1) -(3) шарттарды қанағаттандыратын
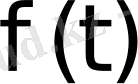 функциясы түпнұсқа деп аталады.
функциясы түпнұсқа деп аталады.
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын
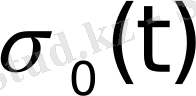 функциясы,
функциясы,
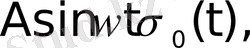
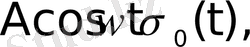
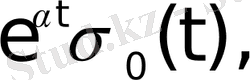
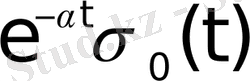
 функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы
 уақыт кезеңі ретінде алуға болады. Сонда t
уақыт кезеңі ретінде алуға болады. Сонда t
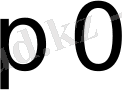 болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген f(t) функциялары үшін орындалады.
Егер осы (1) -(3) шарттардың ең болмағанда біреуі орындалмаса, онда f(t) функциясы түпнұсқа болмайды. Мысалы,
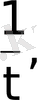
 функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші
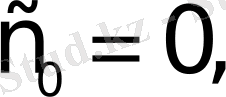 өйткені
өйткені
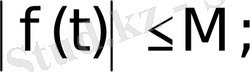
б) Барлық
 түріндегі дәрежелік функциялар. Бұлар үшін
түріндегі дәрежелік функциялар. Бұлар үшін
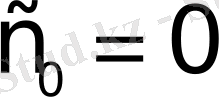 болады. Шынында да
болады. Шынында да
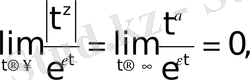
өйткені
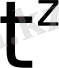 -тің модулі
-тің модулі
 көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
 -қаншалықты болса да аз оң сан.
-қаншалықты болса да аз оң сан.
Осыдан
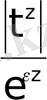 функциясының
функциясының
 аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
 мәндері үшін
мәндері үшін
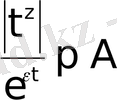 , немесе
, немесе
 теңсіздігі орындалады.
теңсіздігі орындалады.
Мұндағы А-кез-келген оң сан,
 -қаншалықты болса да аз оң сан. Сондықтан
-қаншалықты болса да аз оң сан. Сондықтан
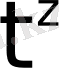 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
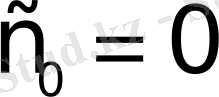 болады.
болады.
Егер
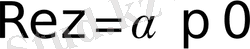 болса, онда
болса, онда
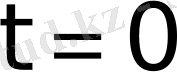 үзіліс нүктесі болады да
үзіліс нүктесі болады да
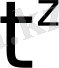 функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Жоғарыдағы
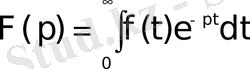 (2. 1)
(2. 1)
теңдігімен анықталған
 комплекс айнымалының
комплекс айнымалының
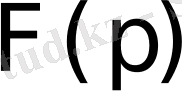 функциясы
функциясы
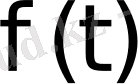 функциясының Лаплас бойынша бейнесі деп аталады. Осы (2. 1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
функциясының Лаплас бойынша бейнесі деп аталады. Осы (2. 1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
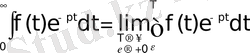 Equation. 3 (2. 2)
Equation. 3 (2. 2)
Мұндағы
 оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
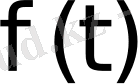 функциясы мен оның
функциясы мен оның
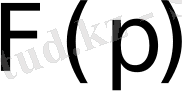 бейнесі арасында сәйкестік орнатылады.
бейнесі арасында сәйкестік орнатылады.
Берілген
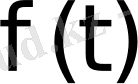 функциясы бойынша оның
функциясы бойынша оның
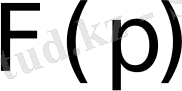 бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
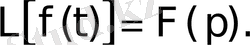 Equation. 3
Equation. 3
Егер
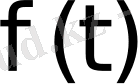 функцияға
функцияға
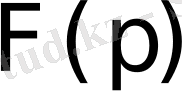 бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
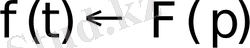 немесе
немесе
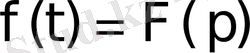 .
.
Егер (2. 2) теңдіктің оң жағындағы шек бар болатын болса, онда Лаплас интегралы жинақталады.
Енді Лаплас бойынша қандай
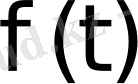 функцияларын түрлендіруге болатынын қарастырайық.
функцияларын түрлендіруге болатынын қарастырайық.
Егер
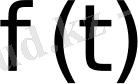 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
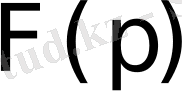 бейнесі
бейнесі
 жарты жазықтығында анықталған.
жарты жазықтығында анықталған.
Мұндағы
 деп
деп
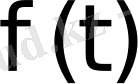 функциясының өсу көрсеткішін ұғамыз.
функциясының өсу көрсеткішін ұғамыз.
Теореманы дәлелдеу үшін р комплекс айнымалысының жазықтығының
 теңсіздігі орындалатын бөлігінде (2. 1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
теңсіздігі орындалатын бөлігінде (2. 1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
Түпнұсқаның (3) шартын пайдаланып мынадай теңсіздіктер аламыз:
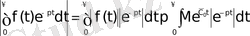
Ал
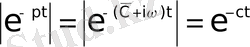 болғандықтан
болғандықтан
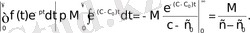 (2. 3)
(2. 3)
Мұндағы
 болғандықтан,
болғандықтан,
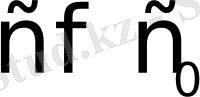
 болса, Лаплас интегралы жинақталады. Сонымен,
болса, Лаплас интегралы жинақталады. Сонымен,
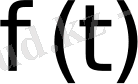 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
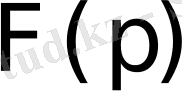 бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
 қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.
қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.

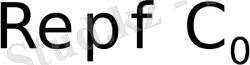
0
 С
С
2. 1. Сурет
Осы теоремадан
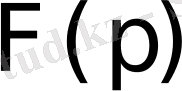 бейнесінің мынадай қасиетін алуға болады.
бейнесінің мынадай қасиетін алуға болады.
Егер (2. 3) теңсіздікте
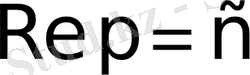 шексіздікке ұмтылса, онда Лаплас интегралының модулі нолге ұмтылады.
шексіздікке ұмтылса, онда Лаплас интегралының модулі нолге ұмтылады.
Осыдан
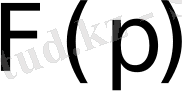 функциясы бейне болса, онда
функциясы бейне болса, онда
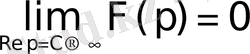 (2. 4)
(2. 4)
болатындығы шығады.
3. Лаплас түрлендіруінің қасиеттері
3. 1 Түрлендірудің сызықтылығы
Егер
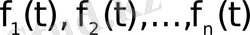 функциялары түпнұсқалар, ал олардың бейнелері тиісінше
функциялары түпнұсқалар, ал олардың бейнелері тиісінше
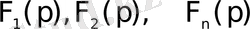 және
және
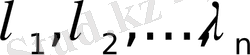 шамалары t-мен р-ға тәуелсіз болса, онда мына арақатынастар орындалады:
шамалары t-мен р-ға тәуелсіз болса, онда мына арақатынастар орындалады:
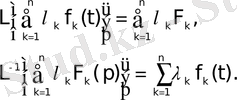 (3. 1)
(3. 1)
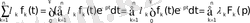
Егер
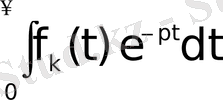 интегралы
интегралы
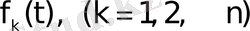 функциялары үшін
функциялары үшін
 жарты жазықтығында жинақталса, онда
жарты жазықтығында жинақталса, онда
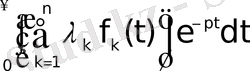 интегралы
интегралы
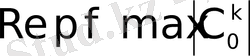 жарты жазықтығында жинақталады.
жарты жазықтығында жинақталады.
3. 2 Түпнұсқаны дифференциалдау
Егер өсу көрсеткіші
 болатын
болатын
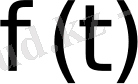 функциясы мен оның
функциясы мен оның
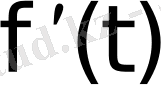 туындысы түпнұсқалар, ал
туындысы түпнұсқалар, ал
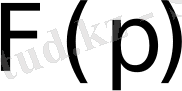 функциясы
функциясы
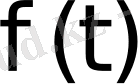 түпнұсқасының бейнесі болса, онда мынадай сәйкестік орындалады:
түпнұсқасының бейнесі болса, онда мынадай сәйкестік орындалады:
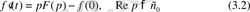
Дербес жағдайда, егер
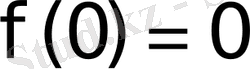 болса, онда
болса, онда
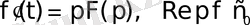 (3. 3)
(3. 3)
Дәлелдеу үшін
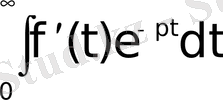 интегралын бөліктеп интегралдаймыз:
интегралын бөліктеп интегралдаймыз:
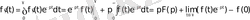
Ал
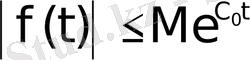 болғандықтан
болғандықтан
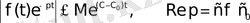
бағалауын аламыз.
Сондықтан
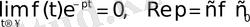 болады да
болады да
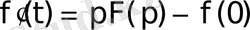 сәйкестігін аламыз.
сәйкестігін аламыз.
Бұл қасиетті жалпылауға болады.
Егер өсу көрсеткіші
 болатын
болатын
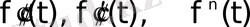 туындылары түпнұсқа болса, онда мынадай сәйкестіктер алуға болады:
туындылары түпнұсқа болса, онда мынадай сәйкестіктер алуға болады:
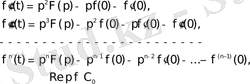 (3. 4)
(3. 4)
Дербес жағдайда, егер
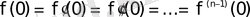 болса, онда
болса, онда
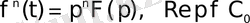 (3. 5)
(3. 5)
3. 3 Түпнұсқаны интегралдау
Егер
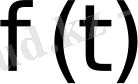 -түпнұсқа, ал
-түпнұсқа, ал
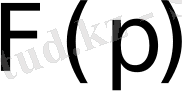 оның бейнесі болса, онда
оның бейнесі болса, онда
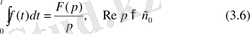
Дәлелдеу үшін
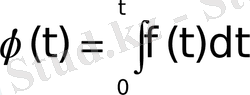 деп белгілейік те, түпнұсқаны дифференциалдау теоремасын пайдаланайық. Сонда
деп белгілейік те, түпнұсқаны дифференциалдау теоремасын пайдаланайық. Сонда
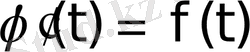 алынады.
алынады.
Егер
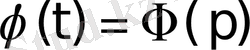 сәйкестігін белгілесек
сәйкестігін белгілесек
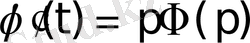 деп жазуға болады. Мұнда
деп жазуға болады. Мұнда
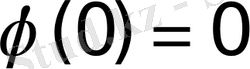 екендігі ескерілген. Ал
екендігі ескерілген. Ал
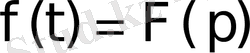 болғандықтан
болғандықтан
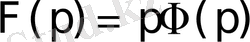 сәйкестігі шығады. Осыдан
сәйкестігі шығады. Осыдан
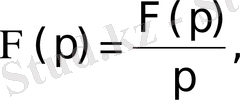 яғни
яғни
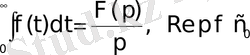 (3. 7)
(3. 7)
3. 4 Ұқсастық теоремасы
Егер
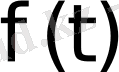 -түпнұсқа, ал
-түпнұсқа, ал
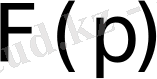 оның бейнесі болса, онда
оның бейнесі болса, онда

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz