Ғарыш және әлем. Әлемді гравитациялық линзалау әдісімен зерттеу

Пән: Астрономия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 56 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

Әл -Фараби атындағы қазақ ұлттық университеті

Монтаева А. А.

ҒАРЫШ ЖӘНЕ ӘЛЕМ. ӘЛЕМДІ ГРАВИТАЦИЯЛЫҚ ЛИНЗАЛАУ ӘДІСІІМЕН ЗЕРТТЕУ.

ДИПЛОМДЫҚ ЖҰМЫС

Мамандық 050611 - “астрономия”

Алматы, 2012

Қазақстан Республикасы білім және ғылым министрлігі

Әл -Фараби атындағы қазақ ұлттық университеті

“Қорғауға жіберілді ”

кафедра меңгерушісі Приходько О. Ю.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы:

“ ҒАРЫШ ЖӘНЕ ӘЛЕМ. ӘЛЕМДІ ГРАВИТАЦИЯЛЫҚ ЛИНЗАЛАУ ӘДІСІІМЕН ЗЕРТТЕУ ”

050611-“Астрономия” мамандығы бойынша

Орындаған Монтаева А. А.

Ғылыми жетекші

ф. - м. ғ. д., профессор Чечин Л. М.

Нормобақылаушы Тлеубаева И. С.

Алматы, 2012

Реферат

Жұмыс 85 беттен тұратын көлемде орындалды. Ол кіріспеден, 3 бөлімнен, қорытындыдан, және 15 атауы кіргізілген пайдаланылған әдебиеттер тізімінен тұрады.

Бет саны 85

Суреттер саны 41

Пайдаланылған әдебиеттер саны 15

Негізгі ұғымдар: гравитациялық линза, геометриялық оптика, оптикалық линза, қараңғы материя, қараңғы энергия, Әлем, Галактиканың құрылымы, Галактиканың морфологиялық жіктелуі, сфералық -симметриялы гравитациялық өріс.

Қараңғы энергия өрістерінде жарық сәулесінің қасиеттері (гравитацилық микролинзалау) сәулеленудің әрекетін зерттеу (спектрлі талдау) және оларды оқытудың тиімді әдістерінің бірі - қараңғы материя болып табылады. Егер спектрлі талдау бариондық материяны зерттеудің бұрыннан құралған әдісі болса, онда гравитациялық линзалау Әлемнің құрылуын зерттеудің жаңа тиімді тәсілі болып табылады. Осы дипломдық жұмыстың мақсаты болып гравитациялық линзалануды детальді талдау әдісі болып табылады. Зерттеу әдістері -тензорлық талдау, гравитациялық линзалау әдісі, жақындау әдісі. Диплом жұмысына пайдаланылған нәтижелер геометриялық оптиканың заңдары, тарту өрісінде жарықтың қозғалысы, Галактиканың морфологиялық құрылымы, вакуумдағы Әлем болып табылады. Жұмыстың жаңалығы қараңғы материя гравитациялық өрісінде жарық сәулесінің ауытқу бұрышын есептеу болып табылады. Бұл Наварро - Френк -Уайт, Баркет және басқалармен құрастырылған. Бұл бұрыштардың 0. 1" қатарда екені көрсетілген. Қазіргі заманғы нақты бұрыштардың өлшемі 0. 001" $\div$ 0. 0001" құрағанымен, қараңғы материяның тығыздығын және есептелген бұрыштардың тікелей өлшенетініне үмітіміз бар.

Мазмұны

Реферат . . .

Реферат . . .: Кіріспе . . .

5: 6

Реферат . . .:

1. Геометриялық оптика

1. 1. Геометриялық оптиканың заңдары . . .

5: 7

Реферат . . .: 1. 2. Оптикалық жұқа линза

5: 7

Реферат . . .: 1. 3. Оптикалық жұқа линзада кескін тұрғызу

5: 9

Реферат . . .: 1. 4. Геометриялық оптикада Ферманың қағидасы

5: 11

Реферат . . .: 1. 4. 1. Жарықтың шағылу заңы

5: 13

Реферат . . .: 1. 4. 2. Жарықтың сыну заңы

5: 15

Реферат . . .: 2. Әлемдегі гравитациялық линзалар

5: 18

Реферат . . .: 2. 1. Гравитациялық линзаның ашылу тарихы

5: 18

Реферат . . .: 2. 1. 1. Жарық сәулесінің ауытқуы қалай тартылады

5: 18

Реферат . . .: 2. 1. 2. Гравитациялық линзаны іздеу

5: 22

Реферат . . .: 2. 1. 3. Гравитациялық линзаны қолдану

5: 24

Реферат . . .: 2. 1. 4. Гравитациялық линзаның ашылуы

5: 25

Реферат . . .: 2. 2. Ауырлық өрісіндегі жарықтың қозғалуы

5: 29

Реферат . . .: 2. 3. Гравитациялық линзаны бақылау

5: 32

Реферат . . .: 2. 4. Гравитациялық линзаның үлгілері

5: 40

Реферат . . .: 2. 5. Гравитациялық линзаның теңдеулері

5: 49

Реферат . . .: 3. Қараңғы материя гравитациялық линза сияқты

5: 52

Реферат . . .: 3. 1. Қараңғы материяның феномені

5: 52

Реферат . . .: 3. 1. 1. Әлемдегі қараңғы материя және қараңғы энергия

5: 53

Реферат . . .: 3. 1. 2. Кеңейтілетін Әлем

5: 54

Реферат . . .: 3. 1. 3. Өткен (бұрынғы) Әлем

5: 56

Реферат . . .: 3. 1. 4. Қазіргі Әлемнің энергия балансы

5: 59

Реферат . . .: 3. 1. 5. Қараңғы материя

5: 60

Реферат . . .: 3. 1. 6. Қараңғы энергия

5: 64

Реферат . . .: 3. 2. Галактиканың морфологиялық құрылымы

5: 65

Реферат . . .: 3. 2. 2. Галактиканың морфологиялық жіктелуі

5: 65

Реферат . . .: 3. 2. 1. Галактиканың құрылымы

5: 67

Реферат . . .: 3. 3. Қараңғы материя галосының сфералық - симметриялық үлгілері

5: 71

Реферат . . .: 3. 4. Галактиканың қараңғы материя галосының гравитациялық өрістеріндегі жарық сәулелерінің ауытқуы

5: 74

Реферат . . .: Қорытынды

5: 76

Реферат . . .: Пайдаланған әдебиеттер тізімі

5: 77

Реферат . . .: Қосымша «Гравитациялық линзалардың фотосуреттері»

5: 85

Кіріспе

Ғарышнама бұл - Әлем эволюциясы және құрылым жөніндегі ғылым. Қазіргі заманғы ғарышнамада көкейкесті және маңызды мәселелердің бірі - қараңғы материя мен қараңғы энергияның физикалық интерпретациясы болып табылады. Бұл феномендерді түсіну - ғарыштық бариондық материя - галактикалар, жұлдызды тұмандық және шағылысудың әсерін оқытуға негізделеді.

Бұл дипломдық жұмыс гравитациялық линзалаудың детальді талдауына арналған

Ол кіріспеден, 13 параграфтан тұратын 3 бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және гравитациялық линзалардың суреттері келтірілген қосымшалардан тұрады. Дипломдық жұмыстың жалпы көлемі 85 беттен тұрады.

Бірінші бөлімде «геометриялық оптика» геометриялық оптиканың негізгі заңдары (жарықтың шағылуы, сынуы, Ферманың қағидаттары) енгізілген.

Екінші бөлімде «Әлемдегі гравитацялық линзалау» гравитациялық өрістерде жарық сәулесінің таралу теориясы қысқаша баяндалған, гравитациялық линзалардың кейбір үлгілері және гравитациялық микролинзалаудың теңдеуі келтірілген.

Соңында үшінші бөлімде «қараңғы материя гравитациялық линзалау сияқты » қараңғы материя жайында, және Галактиканың қараңғы материясы жарық сәулесінің ауытқуы көрсетілген. Қараңғы материя гравитациялық өрісінде жарық сәулесінің ауытқу бұрышын есептедік. Бұл Наварро - Френк -Уайт, Баркет және басқалармен құрастырылған. Бұл бұрыштардың 0. 1” қатарда екені құрастырылған. Қазіргі заманғы нақты бұрыштардың өлшемі 0. 001” $\div$ 0. 0001” құрағанымен қараңғы материяның тығыздығын және есептелген бұрыштардың тікелей өлшенетініне үмітіміз бар.

Дипломдық жұмыстың қорытындысы соңғы бөлімде қысқаша айтылып өткен.

Энштейн теориясына физиктер калай қарайтынын кім біледі, егер, арнайы салыстырмалы теориясы тұтылуды бақылауы «жоққа шығарылумен» аяқталса. Ал жалпы теорияны алдын ала айту, Эддингтон және Дайсон еңбектерінде керемет дәлелденді, 1919 жылы күн тұтылуын бақылау кезінде және релятивисті физикиканың зор жеңісі болып саналады.

Массивті дене жарықты ауытқыта алатынына көз жеткізген соң ғалымдар бұл әрекеттерді ғылым пайдасына қалай іске асыруды ойлана бастады «гравитациялық линза» термині осылайша пайда болды, кәдімгі әйнек линзаға ұқсастығы, сонымен қатар бұл жерде ауытқыған жарық толығымен айқын.

Алғашқылардың бірі болып бұл жерде петрограттық Орест Данилович Хвольсон болды. 1924 жылы ол қысқа «жалған қос жұлдыз жайында» мақала жариялады. Ол мақаласында жарық көзімен линза обьектісі және жер бақылауларының айтарлықтай үлкен қашықтығында алыс көздің кескіндерінің араласуын ғана емес линзасыз болмайтынын жазды. (13 сурет қарау) . Ауытқу бұрышы линзаға жақындағанда үлкейетіндіктен, екінші көріну суретте көрсетілгендей әрқашан қарама - қарсы жақта пайда болады, тек ол линзаның өзінің мөлдір емес денесімен жабылмаса болды. (мысалы, Күнмен жұлдыздар жарығы ауытқу жағдайында) . Хвольсон дұрыс байқағандай, көзге және линзаға бағыттың тамаша түсуінде бақылаушы линза маңайында жарқыраған сақинаны көреді.

14сурет. Галактика

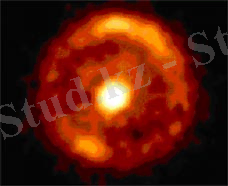
Галактиканың гравитациясы кескіндегі объектіні сақинаға айналдырады

Бұған Эйнштейн - Хвольсон сақинасы мысал . Бұл жерде линза ретіндеден, көз ретіндеде алыс галактикалар шығады. Кескін ортасында көрінетін Галактика-линза, галактика - көз бағытына жақын жерде оның гравитациясы кескіні сақинаға айналады. Объект 1938+66 гравитациялық линзаларды іздеу нәтижесінде радиотелескоп көмегімен ашылды, ол Айдаһар шоқжұлдызында. Линси Кинг және оның қызметтестері Хаббл атындағы ғарыштық телескоп жақын инфрақызыл камера көмегімен осы кескінді алды.

1936 жылы Эйнштейн осындай сақинаның радиусын есептеді, қазір оны Эйнштейн сақинасы деп атайды, тек педанттарда «Эйнштейн-Хвольсон» формировкасын кездестіруге болады. (дегенмен, 1912 жылы жазылған Эйнштейіннің жарияланбаған жазбаларында бұл көріністер жайында ойланғаны байқалады) . Таң қарарлық, XX ғасыр соңында бұндай сақиналар шынымен табылған көз және линза ретінде бақыланып отырған жүйелерде жұлдыздар емес ірі галактикалар алынады.

Эйнштейн компонеттердің бөлшектенуін есептеді «қос жалған», жұлдыздық массаларға және жұлдызаралық қашықтыққа тән. Ол өте үлкен болмады - бұрыштық секунттың мыңнан бірі. Осыдан Эйнштейн шын мәнінде толығымен негізделген линзаның эффектін бақылау шансы зор еместігін қортындылады. Дегенмен ұлы физик ол эффекті емес, ол орыннан емес іздеуді ұсынды.

2. 1. 2 Гравитациялық линзаларды іздеу

Эйнштейн мақаласынан кейін америка астрономы, швейцарлық Франц Цвикки гравитациялық линзаларды басқа жерден іздеу керек екендігін ойлап тапты. Цвикки галактикаларды және олардың жиналуын зерттеумен айналысты. Ол кезде бұл өте жас ғылым еді, аспанда бақыланатын кейбір «тұмандықтың» шын мәнінде үлкен қашықтықта екендігін Хабблдың дәлелдей алғанына жиырма жылда өткен жоқ. Олар жұлдыздардың өте көп санынан тұрады және жиі өз масштабымен жалғыз галактиканы басып алады. Бұл «Млечный Путь -Хаббла» еңбегіне дейін белгілі. (немесе Галактиканы - осылай улкен әріппен жазады, грекше атаумен Млечный Путь, басқа да көптеген галактикалардан ажырату үшін) .

Цвикки Эйнштейн формуласын қолдана отырып галактикада болатын кескіндердің бөлшектенуі доғаның бірнеше секундын құрайды деген шешімге келді. Мұндай қашықтықтар қазіргі заманғы Цвикки телескопының толығымен күшіне сәйкес еді. Тұтылуды күтудің қажеті жоқ: алыс галактикалар онша жарық емес. Дегенмен галактикалар - жұлдыздарға қарағанда тығыз объектілер, олардың массасы Кун массасынан он, жуз миллиард есе басым болсада, олардың көлемі Күннен триллион есе үлкен. Сондықтан көз линза бағытына неғұрлым жақын орналасуы керек, олай болмаған жағдайда кескінді линза өзі жауып қалатын еді. Цвикки гравитациялық линзалар бақылауының ықтималдығын есептеді, оның қорытындысы бүгінді есептерге қарағанда шамалы оптимистірек: Цвикки бағасы бойынша, әрбір төртінші алыс галактикалардың кескіні бөлшектенеді.

Біздің уақытымызда бір көз кескінінің бірнеше компонентке бөлінуі қатты линзалану деп аталады, қатты линзалану объектісі микролинзалану және әлсіз линзалануға қарағанда қатты линзаландырылған деп айтады. Қатты линзаландыруды табудың қиындығы, шыныменде бір - біріне жақын галактикалар тобынан гравитациялық линзалар эффектін бөлу ( соңғысы белгілі болғандай астронамдар айтқандай топқа жиналу «жамырау» немесе «кластерлену» үрдісінде) Бұл екі жағдайды ажырату оңай емес. Біріншіден, нағыз алыс объектілер жұлдызды аспан терең суреттерінде кішкентай дақ сияқты көрінеді. Әрең көрінетін дақты екіншісімен салыстыру, бұдан алысқа баратын шешім - аса мағынасына жеткен іс емес. Екіншіден, нақты көшірмесінен бір кескін екіншісінен үлкен немесе кіші болатындығын күту де болмайды: ғарыштық линзалар өте жетілмеген, заттардың таралуы симметриялықтан өте алыс, себебі бір объектінің кескіні әртүрлі таралуы оригиналғада бір - біріне ұқсамайды.

15 -сурет. Қос квазар QSO0957+561 және екі компоненттің спектірі

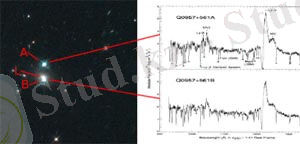
Қос квазар QSO0957+561 - бірінші қос кескін 1979 жылы Вольш, Карсвелл және Вейманн ашқан. Сол жақтағы суретте Хаббл атындағы ғарыштық телескоп көмегімен алынған, екі жарық жұлдызға ұқсаған объект көрінеді, араларында сарғыштау аса ашық емес таңба бар. Бұл таңба галактика линзасы осы. Екі кескінде түстердің ұқсастығы квазар астрономдары олардың сәуленену спектралды құрамын нақты суреттейді. Оң жақтағы графикте Хаббл телескобының көмегімен Андреас Михалициано және әріптестері алған екі компоненттің спектрі келтірілген. Спектрлердің бірдей екендігі көрінеді. Кішкене айырмашылықтары спектр компонентері жарық өтетін галактика линза спектріне жүктелетіндігінен. Бір обьектінің кескіндірін алып атырғанына сенімді болу үшін әдетте астрономдар оның спектрін алады. Спектр - яғни обьектінің қарқынды сәулеленуі жарық толқынының ұзындығына байланысты - жұлдыздар мен галактиканың «қол іздері» деп бекер атамайды. Спектр бойынша көптеген галактикалық сипаттамаларды анықтауға болады, бірақ ен бастысы - алыс галактикаларға дейін қашықтық, олардың химиялық құрамы және өз орбитасы бойынша галактикалар құрған жұлдыздардың айналу жылдамдығы. Бұлардың бәрі спектрларды айтарлықтай дәрежеде дербес етеді. Алайда жәй кескінге қарағанда әлсіз көздің спектрін алу қиынырақ - бұл жеткілікті жарықты жинау ғана емес, шум деңгейінде объектіні бөлектеу үшін қызықтырып отырған әрбір толқын ұзындығы үшін жасау керек. Кескіндерді алуға қарағанда бұған уақыттың анағұрлым көп кететіндігі таң қалдырмайды, ал бұл уақытта шумдардың өздеріде артады.

2. 1. 3. Гравитациялық линзаланудың қолданылуы

Бұл қиындықтардың барлығы гравитациялық линзаланудың ашылуының тағы елу жылға кейінге қалуына алып келді, бұл эффект ешқандай практикалық пайдасы жоқ салыстырмалы теорияның қызықты ізі ретінде қаралды.

60- жылдары жас норвег астрономы Сюр Рефсдал гравитациялық линзаланудың өте маңызды жұмысын тапты. Цвиккида, Рефсдалда линза ретінде алыс Галактика қолданған жағдайды қарады. Бірақта Рефсдалда жарық көзі ретінде оданда алысырақ Галактика шығады, ал көрінетін Әлемнің шекарасында тұтанған - массивті жұлдыздың жарық өмірінің соңғы салюті, кішкентай обьектіге айналар алдында қара тесікке немесе нейтронды жұлдызға айналатын өзінің сыртқы қабаттарын лақтырады. Тұтану кезінде алғашқы бірнеше күнінде оның ата - аналық галактикасы сияқты «жұлдыз» жарық жарқырайды, бірақ солай бола тұра галактикалар кескінін ұсынушы жарық «анық емес» барлық дақтарда емес, сондықтан оны фиксирлеу оңайырақ. Галактиканың екі еселенген кескінін бақылаған астрономдар тұтану кезінде нені көреді? Жауап аса қу емес - әрбір кескінде бір жұлдыздан тұтанады, бір - бірінің нақты көшірмесі болады. Алайда Рефсдал бір нәрсені түсінді: әрбір кескінде пайда болатын жарық сәулесі әр жолда өтеді, сондықтан әртүрлі кескіндердің арасында кідіріс байқалады: әуелі бөлшектенген кескіннің компонентері тұтанады сосын басқасында қанша болсада барлық кескін бойынша тұтанады. Сондада уақытша кідіріс бір жағынан геометриялық жүйенің жол ұзындығынан анықтадады, ал екінші жағынан - астрономиялық тәсілмен өлшенуі мүмкін: бүгінгі күнге дейін - физикада анағұрлам нақтырық өлшенген шама. Сәйкесінше, астрономдар қолына геометриялық өлшемдер өлшемі бірегей зат түсті. Тәсілдің практикалық қолданысын қиындатқан көп мәселелері шықты, олардың сәтті ұзаруы маңызды параметрді өлшеуге мүмкіндік береді - тұрақты Хаббл. Ол Әлемнің кеңейу жылдамдығын, оның геометрикалық өлшемдерін, ең бастысы жасын анықтайды.

Рефсдал тұтану жайында айтты, бірақ мұндай тұтанулар жиі болмайды - әрбір галактикада жүз жылда бір тұтанады. Осы уақытта линзаны ұстау мүмкіндігі көп емес, егер біз көптеген линзаларды үнемі бақыламасақ. Дегенмен істе көзден тек қана өзінің жарығын өзгерту ғана талап етілді, әр түрлі компоненттер кескінін өлшеуі ұқсас келгенде уақытша жылжуды анықтау үшін. Мұндай көздер Рефсдал еңбегінен бір жыл бұрын, 1963 жылы табылды. Бұл квазарлар - кішкентай, бірақ жарық қара жырық миллиардқа дейін Күн массасы салынған галактикалық ядро. Жұлдыздарды жара және заттарды жұта қара жырық квазарды жарық болуға мәжбүрлейді, бақыланатын Әлемнің ең шетінде оларды бақылауға мүмкіндік береді. Сондада қара жырықтың режимі тұрақты емес, жылтыраудан квазар тез әрі жиі өзгереді. Өшірілуі және жарығы квазарларды гравитациялық линзалар үшін жарық көзі басты кандидаты етті, ал жылтарау ауыспалы - өлшеу үшін жақсы құрал тұрақты Хабблды Рефсдал тәсілімен есептеу үшін жақсы құрал.

2. 1. 4. Гравитациялық линзалардың ашылуы

1979 жылы алғашқы линза табылды. Үш америка астрономдары - Денис Вольш, Боб Карсвелл и Рэй Вейманн - «қос квазар» кездейсоқ тапты. Олар тез арада QSO0957+561 атауын алғашқы квазардың қосарланған кескінін көрсетеді; линза сияқты әрекет ететін галактиканы да тапты. Алты жылдан кейін Хучра және оның әріптестері ең белгілі объект - квазар төрт кескіні QSO2237+0305, немесе «Эйнштейн кресті». Осы крестке ары қарай айтылатын маңызды эффект микролинзаландыру.

16 -сурет. Эйнштейн кресті

Алыс квазардың төрт түсіру компоненті QSO2237+0305 - «Эйнштейн кресті». Қазіргі уақытта квазар бізден 8 миллиар жарық жыл орналасқан - осы түсіруде жақсы көрінетін галактика линзаға қарағанда 20 есе арырақ. Жүйе өте симметриялы сондықтан әртүрлі түсірулер арасындағы уақытша кідіру небәрі бірнеше сағатты құрайды. Соңғы түсірулер арасындағы квазар объект - бұл галактикалар ядросы, оның спектрі квазарлар спектрлеріне мүлдем ұқсамайды. Бұл түсіруді Джеймс Роудс 3, 5-метрлі АҚШ Китт-Пик тауындағы телескоп арқылы алған.

Келесі ғасырдың төрттен бірінен артық уақытта астрономдар бір қарағанда идеялардың практикалық іске асырылуы қандай қиын болатындығына көз жеткізді. Осы жағдайда бұл жалпы тұжырым Рефсдал бойынша тұрақты Хаббл өлшеу әдісіне қатысты.

Біз түсірулер арасындағы кідіріс жол ұзындығымен анықталатынын айтқанда, аздап алдадық. Шын мәнінде арнайы салыстырмалы теория жағдайында ғана солай болатын еді. Бұл жағдайда жарық сәулесінің ауытқуы линзаға жақын өтетінін ескерсек, үштікті оңай шешуге болады және түсірудің бақыланып отырған қалпынан олардың бір - бірінен бөлініп шығу арқылы ұзақ жолын табуға болады. Алынған кідіріс геометриялық атауда және тұрақты Хабблды тұтынады. Алайда бұл жерде іске гравитацияның шын мәніндегі теориясы бұл жалпы салыстырмалы теория деген факт тағы да араласады ( қалай болғандада қазіргі мәліметтермен шындыққа жақын) . ОТО да гравитация бөлшектердің қозғалыс траекториясын ғана анықтап қоймайды, сонымен қатар, жарықты сол және басқа жерде сағат жүрісінің темпін де анықтайды. Тартылатын орталыққа жақын уақыт ақырын жүреді, әрі кішкене тезірек. Сондықтан, линзадан әртүрлі қашықтықта өткен жарық сәулесі кеңістік аумағынан әртүрлі сағат жүрісінің темпімен өтеді және әртүрлі кідіреді. Бұл кідірістің екінші уақыты, ол потенциалды деп аталады және бақылаудан алынған жалпы кідірісті алу үшін оны геометриялыққа қосу керек. Сәйкесінше, тұрақты Хабблдан тәуелді геометриялық бөлігін алу үшін бақыланып отырған мәліметтетден потенциялды кідірісті дұрыс есептеу керек. Міне проблема осында. Потенциялды бөлімін есептеу үшін линзада массаның таралуын білу қажет, бақылаулардың тура екендігін анықтау. Астрономдар түсірудің әрбір компонентін, оның өлшемін, формасын, жарықтығын жағдайын анық алдын ала айта алатын линза моделін құру үшін аз күш жұмсамады. Егер соңғылары болып кетсе онда, тұрақты Хаббл анықтамасы да сәтті болады. Дегенмен бақылаулардан толық кідірісті анықтау да оңай жұмыс емес. Оны жүргізу үшін компонентердің бірінің қандайда бір сипатты деталін, жалтырау кезінде өзгерісін табу керек - мысалы, жұлдыздық шамадан жарқыраудың бірден көтерілуі - сосын басқа компонентің қисық жалтырауына деталімен теңестіру және олардың қашықтығын өлшеу. Алайда бұл үшін екінші компонентті бірінші компонентпен бір уақытта бақыламау керек, ал кейінірек - бір - бірінен салыстырмалы белгісіз уақыт кідірісінде. Ал бұл уақыт бірнеше сағат немесе бірнеше жыл құрауы мүмкін.

Гравитациялық линзалардың осы проблемаларды шешуге көмектесетін тұрақты мониторинг бағдарламалары бар, бірақ уақыт телескоптардың бәріне бірдей жетпейді, мәліметтерде ұзақ кемшіліктер бар және өлшем нақтылығы абсолютті емес. Қорытындысында, кідірісті анықтау үшін стилистикалық өңдеудің күрделі әдістері қолданылады және қисық жарқырау теңестіріледі. Осы зерттеулердің қорындысы бірнеше жүйелерде кідіріс анықтамасы және шамамен 15 миллиард жыл Әлемнің жасын болжайтын тұрақты Хабблдың бағасы болды. Осындай өлшеулердің саны онға және жүзге жеткенде, астрономдарда алғашқы галактикалар құрылғаннан бастап жақын уақытқа дейінгі Әлем көлемінің өзгеру тарихын өлшеуге мүмкіндіктері туды.

Қазіргі уақытта шамамен жүздеген квазарлар және галактикалар белгілі, гравитациялық линзалану екі, төрт кейде көптеген компонеттерге бөлшектенуін түсірді. Ал 1987 жылы алғашқы «Эйнштейн сақинасы» табылды, ашылу радиотелескоптың көмегімен болды - гравитациялық линзалану, эквивалент принципімен сәйкестенуі, жарық толқынының ұзындығын айырмайды. Қазіргі уақытта зерттеудің гравитациялық линзалану бойынша айтарлықтай бөлімі радиодиапазонда өтеде, және дәл осы кезде ондаған «сақина» белгілі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.