Генераторлар негізіндегі телекоммуникациялық жүйелер

КІРІСПЕ
1. ЛОГИСТИКАЛЫҚ БЕЙНЕЛЕУ ГЕНЕРАТОРЫ ЖӘНЕ ОНЫҢ СҰЛБАСЫ
2. ЛОРЕНЦ ГЕНЕРАТОРЫ ЖӘНЕ ОНЫҢ СҰЛБАСЫ
2.1 Тәжірибе нәтижелері
3. «ЖИНАҚТАУ.ЛАҚТЫРУ» ГЕНЕРАТОРЫ
3.1 Тәжірибе нәтижелері
4. ГЕНЕРАТОРЛАР НЕГІЗІНДЕГІ ТЕЛЕКОММУНИКАЦИЯЛЫҚ ЖҮЙЕЛЕР
4.1 Логистикалық бейнелеу генераторы
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

Қазіргі уақытта информациялық технологияның қарқынды дамуынан және техникалық құрылымдарды түрлендіруді жүзеге асыруынан, информацияны жіберу мен сақтау жөнінде жаңа мәселелер көбейіп қана койып жатқан жок, онымен қоса бізге белгілі техникалық мәселелердің шешімдерінің саны да көбеюде. Бұл үшін жаңа техникалық амалдарды іздестіру мен құру жүріп жатыр. Мәселенің өзектілігі, нақтылап айтсақ, информацияны жіберуде құпиялықты қамтамасыз ету болып табылған және болып қалмақ. Бұл мәселені шешу жолдарының бірі хаосты сигналдарды (ХС) қолданумен байланысты. Хаосты сигналдарды қолданудағы техникалық байланыс жеткілікті түрде жақсы қарастырылған және қазіргі уақытта қарқынды дамуын жалғастырып келеді. Техникалық байланыста, информацияны жіберудегі құпиялылықты шешуде жаңа нәтижелер көрсететін тағы бір болашағы бар бағыт бар.

1. Жанабаев З.Ж., Ахтанов С.Н. Новый метод исследования бифуркационных режимов по реализации динамической системы // Вестник КазНУ. Серия физическая № 1 (44), 2013, с.67-78.
2. Madhekar Suneel. Electronic circuit realization of the logistic map // Sadhana, Vol. 31, Part 1, February 2006, pp. 69–78.
3. Гонченко А.С., Гонченко С.В., Шильников Л.П. К вопросу о сценариях возникновения хаоса у трехмерных отображений // Нелинейная динамика. 2012. Т. 8. № 1. S. 3–28.
4. Иванов А.П. Исследование разрывных бифуркаций в негладких динамических системах, // Нелинейная динамика. 2012. Т. 8. № 2. S. 231–247.
5. Akhtanov S. N., Zhanabaev Z. Zh., Zaks M. A. Sequences of gluing bifurcations in an analog electronic circuit // Physics Letters A.-2013.-Vol. 377.-P.1621–1626.
6. Анищенко Б.С., Бирюкова Н.И., Астахов С.В. Время возврата Пуенкаре и локальная размерность хаотических аттракторов // Нелинейная динамика. 2012. Т. 8. № 3. S. 449–460.
7. Кузнецов А.П., Поздняков М.В., Седова Ю.В. Связанные универсальные отображения с бифуркации Неймана Сакера // Нелинейная динамика. 2012. Т. 8. № 3. S. 473–482.
8. Thompson J.M., Stewart H.B. Nonlinear Dynamics and Chaos // John Wiley & Sons, England. 2002. 458 p.
9. Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания // М.: Физматлит, 2002, 292 с.
10. Rulkov N.F. Modeling of spiking-bursting neural behavior using two-dimensional map // PhysRevE, Vol. 65, 041922 (2002)
11. Жанабаев З.Ж., Ахтанов С. Н. Универсальное отображение перемежа-емости // Вестник КазНУ. Серия физическая №2 (37). 2011, с. 15-25.

Пән: Автоматтандыру, Техника
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

Кіріспе

Қазіргі уақытта информациялық технологияның қарқынды дамуынан және техникалық құрылымдарды түрлендіруді жүзеге асыруынан, информацияны жіберу мен сақтау жөнінде жаңа мәселелер көбейіп қана койып жатқан жок, онымен қоса бізге белгілі техникалық мәселелердің шешімдерінің саны да көбеюде. Бұл үшін жаңа техникалық амалдарды іздестіру мен құру жүріп жатыр. Мәселенің өзектілігі, нақтылап айтсақ, информацияны жіберуде құпиялықты қамтамасыз ету болып табылған және болып қалмақ. Бұл мәселені шешу жолдарының бірі хаосты сигналдарды (ХС) қолданумен байланысты. Хаосты сигналдарды қолданудағы техникалық байланыс жеткілікті түрде жақсы қарастырылған және қазіргі уақытта қарқынды дамуын жалғастырып келеді. Техникалық байланыста, информацияны жіберудегі құпиялылықты шешуде жаңа нәтижелер көрсететін тағы бір болашағы бар бағыт бар. Ол бағыт кең жолақты хаосты сигналдарды қолданумен байланысты. Кең жолақты тербелістердің байланыс жүйесін қолдануға арналған жұмыстар саны қарқынды өсуде. Бұл бағыт бейсызық динамиканың қарқынды дамуында "динамикалық немесе детерминирленген хаос" деп аталатын құбылыс пайда болғаннан кейін ғана пайда болды. Кейбір динамикалық жүйелерде, белгілі бір шарттар орындалғанда, бейсызық тербелістердің ерекше түрлері пайда болатыны анықталды. Олардың спектрі қарапайым шуылдық процесстің спектрінен айырмашылық жасамайды, бірақ осы тербелістерді жүзеге асыратын арнайы алгоритмдер бар.
Детерминирленген хаос негізіндегі байланыс жүйесін жасау болып табылатын техникалық мәселенің шешімі- информацияны жіберуді құпиялылықпен қамтамасыз етудің бір тәсілі болып табылады. Бірақ хаосты тербелістерді информациялық технологияда қолдану тек байланыс жүйесімен ғана шектеліп қоймайды. Қарқынды жүйелерде информацияны түрлендіру процессі, хаосты тербелістерден пайдалы информацияны бөліп алған кездегі түрлендірумен көп ұқсастық болады деген мәліметтер бар. Дәл осы негізде құрылымы жағынан және ұйымдастыру жағынан жады жүйесіне ұқсайтын жаңа типтегі жады жүйесін жасауға мүмкіндік бар.
Детерминирленген хаосты тербелістердің ең негізгі ерекшелігі олардың үлкен информациялық сыйымдылығында, ал олардың информацияны жіберу жүйесінде қолдану мүмкіндігі, ең алдымен олардың техникалық қолдануға қажетті, хаосты тербелістерді қанша рет болмасын алу негізіндегі белгілі детерминирленген алгоритмнің болуымен байланысты.
Дипломдық жұмыстың мақсаты: детерминирленген хаос генераторының физикалық модельдерін құру, олардың макеттерін жасау және олардың құрамын зерттеу. Негізінен генератордың жұмыс істеу режимін басқару сұрақтарына және олардың жұмыстарын хаосты режимде тұрақтылыққа зерттеуге көп көніл бөлінеді.
Дипломдық жұмыстың өзектілігі: Техникалық тапсырмаларды шешу кезінде информациялық технологияда және информацияны жіберу жүйесіндегі детерминирленген хаостың қолдануымен байланысты пайда болатын қиыншылықтар берілген параметрлермен хаосты тербелістерді алу және оларды басқарудағы сұрақтардың қажеттілігімен негізделген. Сондықтан да хаос генераторының физикалық моделін жасау және олардың құрамын зерттеу детерминирленген хаостың қолданысы негізінде жұмыс жасайтын байланыс жүйесін құру үшін техникалық тапсырмаларды шешудегі керекті бастама болып табылады.
Қазіргі зерттеулерде жүйенің күйінің сапалы өзгерістерін анықтайтын әр түрлі динамикалық жүйелерде бифуркация қарастырылып жатыр. Бифуркациялық диаграммалар динамикалық жүйенің теңдеуінде берілетін басқарушы параметр мен физикалық өлшемнің максималды және минималды мәндерімен тәуелділігі құрылады.
Жүзеге асыру генераторы ретінде бұрын сонды зерттелген, тәртіп параметрі алдын ала белгілі болатын логистикалық бейнелеу, Лоренц генераторы және "жинақтау-лақтыру" сияқты динамикалық жүйенің модельдері таңдалынды.

1. Логистикалық бейнелеу генераторы және оның сұлбасы

Хаосты режим логистикалық бейнелеу генераторы алгоритмі негізіндегі сигналдың бейсызық түрленуі нәтижесінде алынған аналогты генераторды қарастырайық. Бұл принцип бойынша жұмыс істейтін физикалық модельдер әлі зерттелмеген. Логистикалық бейнелеудің аналогты моделі детерминирленген хаос генераторын құруда бұрын соңды қолданылмаған.
Генератордың ұсынылып отырған физикалық моделі "логистикалық бейнелеу" деген атпен белгілі алгоритмнің моделдеуін жүзеге асыратын электронды схема түрінде көрініс табатын құрылғы негізінде жасалған: [1]

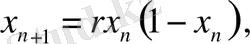(1.1)

мұндағы 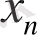- құрылғының кірісіндегі сигнал, 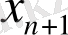- құрылғының шығысындағы сигнал, 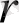- құрылғының құрамына кіретін күшейткіштің күшейту коэффиценті.
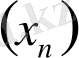кіріс сигналы және 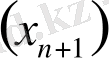шығыс сигналы (1.1) қатынаспен байланысқан бейсызық түрлендіргіштің құрылымдық сұлбасы, 1.1- суретте көрсетілген.

Xn
Xn+1
λ
1
2
3

Сурет 1.1. Аналогты модельдеу қатынасының сұлбасы :
1- r күшейткіші бар күшейткіш, 2- аналогты көбейткіш, 3- дифференциалды күшейткіш.

Бейсызық динамикалық жүйенің белгілі бір түрі дискретті уақытта келесідей сипатталады: [2]

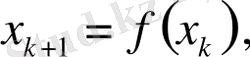
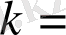0, 1, 2 , (1.2)

мұндағы, 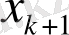- келесі күйді білдіреді. Сондай-ақ, 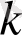- дискретті уақытты білдіреді.
Логистикалық бейнелеу күй теңдеуімен сипатталатын динамикалық жүйе болып табылады.

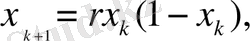
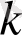=0, 1, 2, (1.3)

мұндағы, және 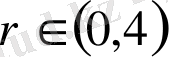. 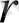- басқару параметрі ретінде белгілі [3].
(1.3) теңдеу 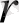шамасына тәуелді. 0 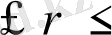1 үшін жүйе әрқашан х= 0 тұрақты жағдайға үйлеседі. Бұдан басқа, 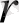= 1 болғаннан бастап жүйе 0- ге келуді тоқтатады, оның орнына басқа фиксацияланған нүктеге үйлеседі.
1 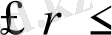3аралығында әрбір r мәні басқа х тұрақты жағдайына ие. 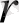= 3 - ке тең болғанда жүйенің кез- келген фиксацияланған нүктеге бекітілуі тоқтайды. Оның орнына, ол екі жағдайдың арасында- бифуркация секілді көріністе ауытқи бастайды.
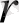- дің мәні 3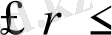3.57 аралығында қосымша ұлғайғанда, жүйе еселену кезеңі деп аталатын кезеңде төрт жағдай, сегіз жағдай, он алты жағдай арасында ұзақ уақыттық ауытқымалы көрініске әкелетін бірқатар бифуркациядан өтеді. 3.58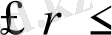4 аралығында, жүйенің қозғалысы үйлесімсіз және де периодты емес болады. Айнымалы жағдайда соңғы көбею мәнінің орнына үздіксіз аралықты толтырады. Мұндай құбылыс хаос (ретсіздік) деп аталады және жүйе хаосты режим деп айтылады. Бұдан басқа, 3.58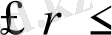4 аралығында хаосты аймақтар кезектесу деп аталатын кезеңділіктің қысқа терезесімен кезектеседі. Жүйенің кешенді қозғалысын х пен r- дің ұзақ уақыттық мәні арасындағы құрылған графигін зерттей отырып түсінуге болады.
Хаосты динамиканың қызықты ерекшеліктерінің бірі бастапқы шартқа шекті сезімталдығы. Бұл сезімталдықтың нәтижесі кеңістікте жақын, жылдам таралатын және біршама уақыт өткеннен кейін корреляцияланаған түрге айналатын, екі нүктеден шығатын екі ретсіз траектория болып табылады. Бастапқы күйді физикалық өлшеу әдетте кейбір қателіктердің санымен байланысты және бастапқы мәнге сезімталдылығы оның алдағы ұзақ мерзімді уақыттағы хаосты орбитаны анықтаудың мүмкін еместігіне алып келеді. Бұдан басқа, екі бірдей жүйе бірдей орбитаға әкелмейді, өйткені орбиталардың таралуы және корреляциялануы үшін жеткілікті болатын бастапқы жағдайдың минуттық табиғи айырмашылықтың болуы міндетті болады.
Сандық тәсілдермен компьютерлік модельдеуден алынған хаосты траекториялар шын мәнінде әрбір қадамда болатын жақындаулардың нәтижесінде механизмдердің соңғы нақтылығына байланысты периодты болатынын атап кету қажет. Бұдан басқа, есептелген шешімдер жағдайлардың табиғи вариациясына байланысты болмайды, орбиталарға бірдей бастапқы шарттар қамтамасыз етілгенде бірдей орбиталардың генерациясынан детерминирленген және бірдей алгоритм болып табылады.
(1.3)- ны жүзеге асыру үшін блокта кіріс- шығыстың болуы болжанады:

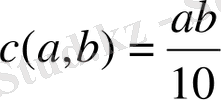, (1.4)

мұндағы, a,b - кіріс кернеулері, с- шығыс кернеуі. Бұл микросхемалар көбейткішінің коммерциялық қол жетімді аналогының кіріс-шығыстық сипаттамасы болып табылады. (1.3) теңдеуде айнымалы жағдайдың мәндері (0,1) аралығында жататынын атап кету қажет. Сонымен бірге, көптеген аналогты микросхема көбейткіші кіріс кернеуінің -10В- тан 10 В дейінгі жұмыс диапазонына ие. Сондықтан, сигналдың аз кернеуінде қателіктерді болдырмау үшін, айнымалы жағдайды 10 коэффициентімен ауқымдау қауіпсіз болады. Осы себепке байланысты, r басқару параметрінің мәні 2.5 коэффициентімен кеңейтілуі мүмкін. Бұны мыналарды ауыстыра отырып құрайды:

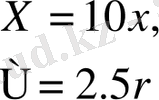(1.5)

(1.3)- тегі бұл ауыстырулар ықшамдағаннан кейін:

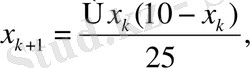(1.6)

шығады.
Сурет 1.2- нің тұйықталу схемасы (1.6) теңдеуді жүзеге асыру үшін ұсынылады. Сұлбада, А1 дифференциалды күшейтіштің жеке күшею болып табылады. М1 мен М2 (1.8) теңдеумен берілген кіріс-шығыс сипаттамасымен аналогты көбейткіш блоктар болып табылады. А2 күшею коэффициенті 4-ке тең сызықты күшейткіш болып табылады. М2-нің шығыстардың біреуі ˄- ге тең тұрақты тоқтың кернеуі болып табылады.

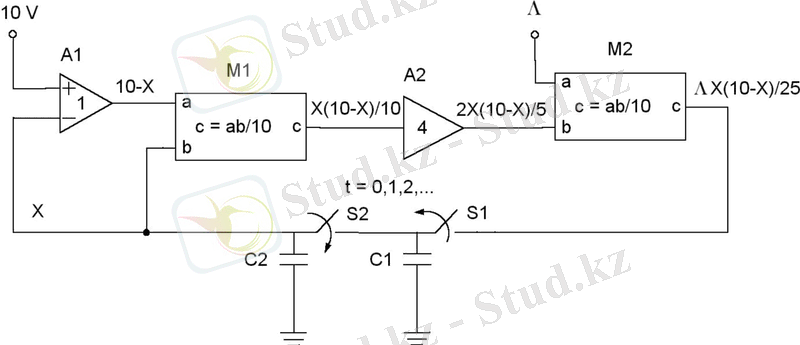
Сурет 1.2. (1.6) теңдеуді жүзеге асыру блок-схемасы [2]

Екі қосылған конденсатор жұптардың әрбірі селективті ұстау блогынан тұрады. S1 және S2 кілттері келесідей режимде жұмыс істейді: кілттердің біреуі жабық болғанда, сол арада екіншісі ашық тұрады. Х- тің соңғы мәні S1- ді жаба отырып дискретті болғанда, S2 ашық қалады және Х- тің алдыңғы мәні С2 болып қалады. Соңғы мән дискреттелгеннен кейін және С1 осы мәнге дейін қуатталған соң, S1 ашылады және S2 жабылады. Кейін С2 соңғы мәнге дейін қуатталады және Х- тің келесі мәні есептеледі де, дискреттелу үшін мүмкін болады. Осы екі селективті ұстау блогы жүйенің дискретті уақыт сипатына бірге жауапты болады.
Хаосты генераторды алу үшін (сурет 1.2) құрылымдық сұлбалы құрылғыға оң кері байланысты тізбек жалғанады. Нәтижесінде сурет 1.3-те көрсетілген сұлба алынады.

Xi

r
1
-
3
reg
4
2
Xi+1

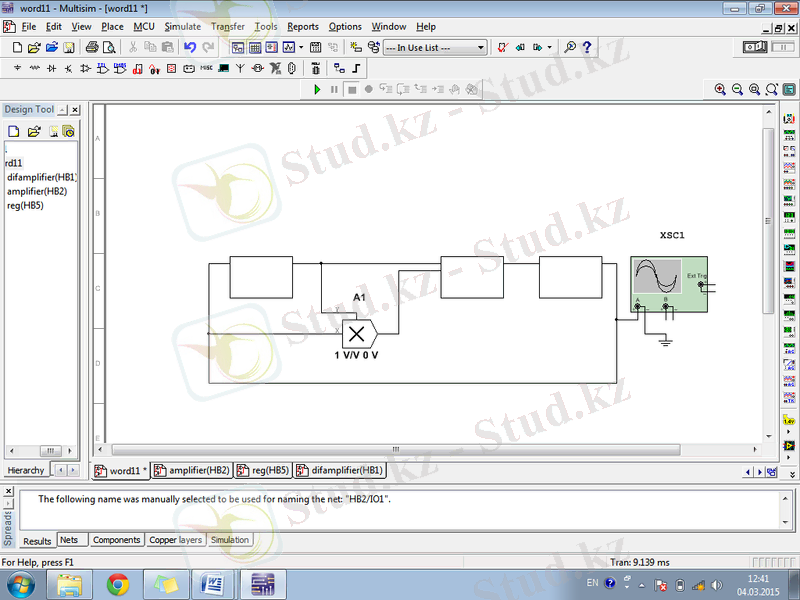
Сурет 1.3. Логистикалық бейнелеу генераторының аналогтық блок-схемасы
мұндағы, 1 - r күшейту коэффиценті, 2 - аналогты көбейткіш, 3 - дифференциалды күшейткіш, 4 - регистр

(1.3)- сұлбаны жүзеге асыру аналогты интегралды схемалар мен компоненттерді қолдану арқылы жүргізілді. 1- ші және 3- ші блоктар National Semiconductor-дағы виртуалды операциялық күшейткіштердің көмегімен жүзеге асырылған. Интегралды схемадағы аналогты көбейткіш 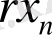және 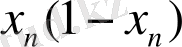көбейтінділерін жүзеге асыру үшін қажет.

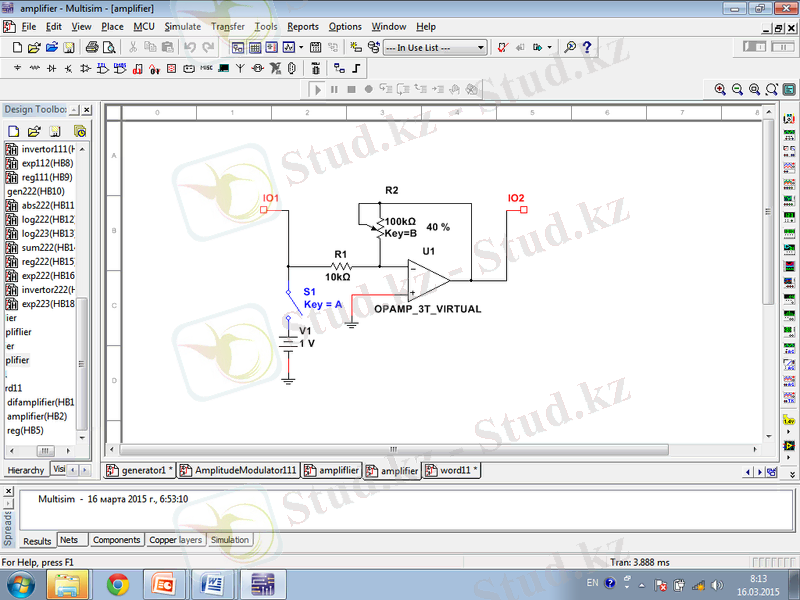
Сурет 1.4. Операциондық күшейткіштің сұлбасы

Операциялық күшейткіш - дифференциалды кірісі, тұрақты ток күшейткіші және үлкен күшейту коэффиценті бар жалғыз ғана шығысы бар күшейткіш. ОК көбіне алынған сұлбаның жіберу коэффицентін тез анықтайтын ОК-ның үлкен күшейту коэффицентінің арқасында үлкен теріс кері байланысы бар сұлбаларда қолданылады. Қазіргі кезде ОК жеке чиптер ретінде сондай-ақ күрделі интегралды сызбалардың құрамында функционалды блок ретінде үлкен қолданыс тауып келеді. Осындай танымалдылық ОК сипаттамаларымен, идеалдыға жақын, негізінде көптеген әр түрлі электронды түйіндерді құруға болатын универсалды блок болып табылуымен келісілген [4].

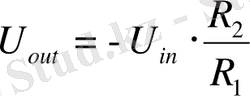(1.7)

А2 күшейткішінің күшейту коэффиценті айнымалыны оның инверттеуші кірісі мен жердің арасында айнымалы резисторды қамтамасыз ете отырып сақтады. Айнымалы күшейткішпен осы күшейткіш үшін күшейтудің өзгертулерін қалпына келтіруге мүмкіндік жасайды. Айнымалы резистордың қажеттілігі, яғни тактілі жиілікті өзгертіп отыру үшін, жұмыс уақытында сұлбаға деген ең оңтайлы мән алу үшін қажет.

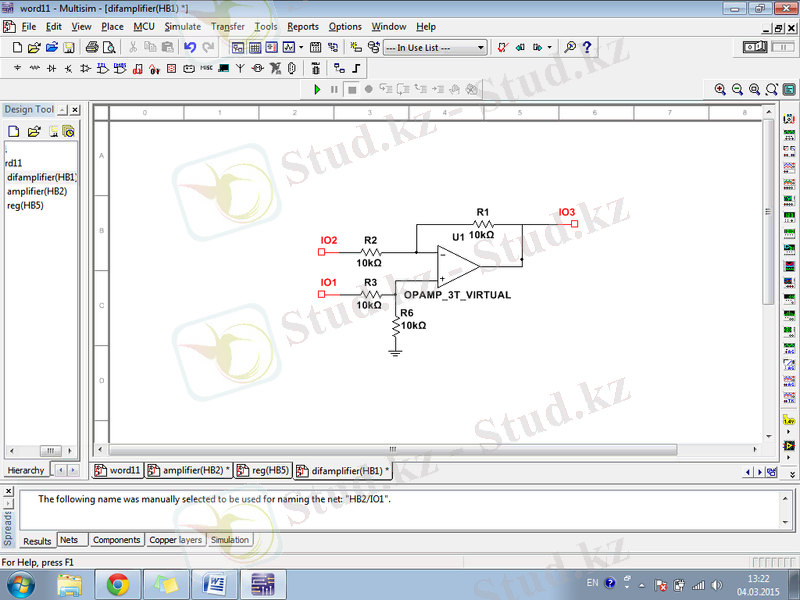
Сурет 1.5. Дифференциалдық күшейткіштің сұлбасы

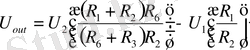
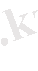(1.8)

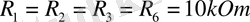болғандықтан, 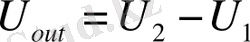болды.
Дифференциалды күшейткіш екі кіріс сигналдың кернеуінің айырмасын күшейту үшін қолданылатын сұлбаны сипаттайды. Біздің жағдайымызда шығыс сигнал кіріс сигналдың әрбір деңгейіне тәуелді емес және олардың айырмасымен анықталады. Екі кірісте де сигналдың деңгейі бір уақытта өзгерген кезде, кірістің дәл солай өзгеруі синфазды өзгеру деп аталады. Дифференциалды күшейткіш немесе айырымды күшейткіш синфазды сигналды азайтудың үлкен коэффицентімен қамтамасыз етілген. Дифференциалды күшейткішті әлсіз сигналдар шуылдардың арасында жоғалып жатқан жағдайларда қолданылады. Дифференциалды күшейткіштің жұмыс істеу принципі дифференциалды сигналды күшейту және қарапайым сұлбалар жұмыс жасайтын ассиметриялы сигналдарды тудыру болып табылады.

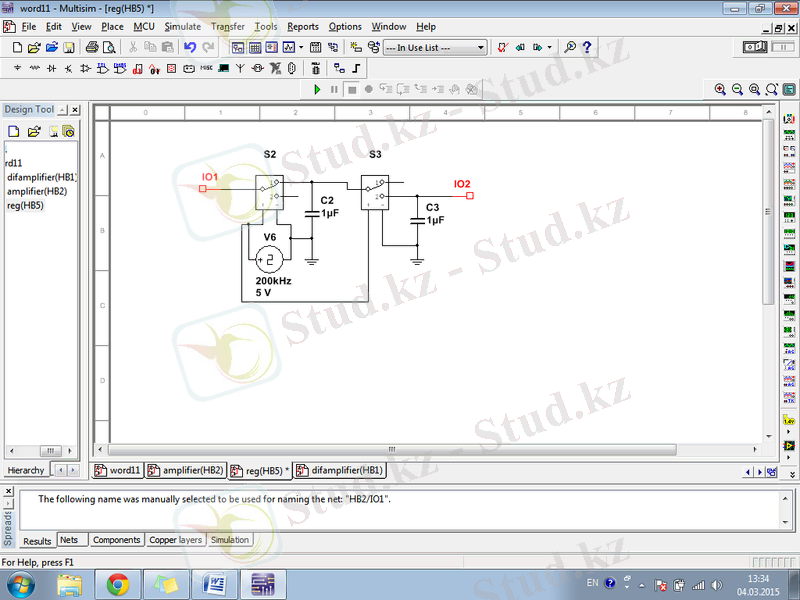
Сурет 1.6. Регистрдің сұлбасы

Регистр- қарапайым түрлендірулерді қабылдауға, сақтауға және екілік сандарды жіберуге арналған тізбекті құрылғы. Қарапайым түрлендіргіштердің астында сандардың берілген разряд санына жылжуы байқалады. Регистрдың негізгі элементі регистрдің разрядтары арасында әр түрлі байланыстарды тудыру үшін және операндалардың тарату мен қабылдауын басқару үшін комбинациялық логикалық элементтермен толтырылатын триггерлер болып табылады. Регистрдің негізгі функционалды қызметі- көпразрядты екілік сандар үшін оперативті жадының қызметін атқарады. Екілік инфомацияны қабылдау мен тарату әдісіне қарай регистрлерді параллелтді, тізбекті, тізбекті-параллельді, параллельді- тізбекті және универсалды деп бөледі. 1- ші кілт қосылғанда С2 конденсатор жұмыс істейді, ал бұл кілт жабылғанда С3 конденсатор жұмыс істейді. Регистр әрбір Xi моментін сақтап отыру үшін қажет.

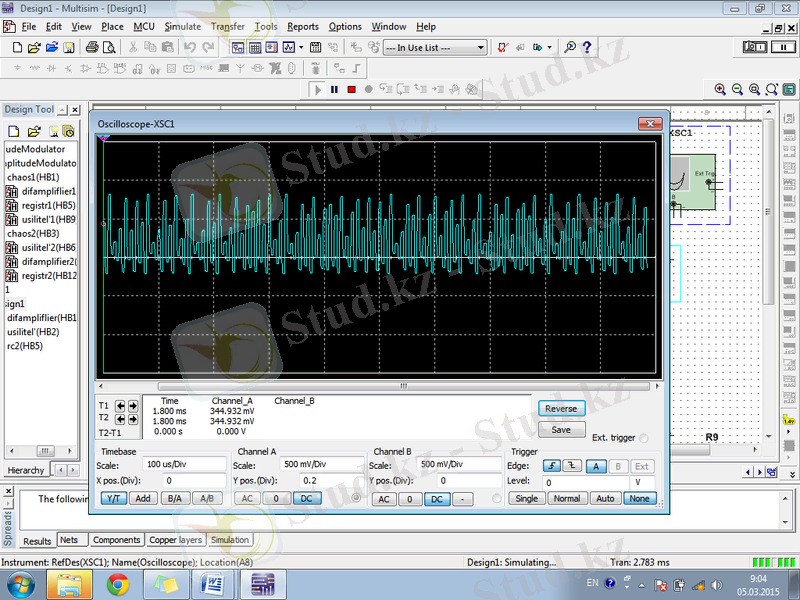
Сурет 1.7. Логистикалық бейнелеу генераторының шығысында алынатын график

Генератордың жұмысын сапалы түрде келесідей түрде сипаттай аламыз. Оң кері байланыс тізбегінің болуы сигнал бейсызық түрлендіргіш арқылы өткен сайын (1) қатынасқа сәйкес өзгертулерге тұрақты болады. Ол барлық процесске болғанда түрлендіруімен ұқсастық алып келеді. Сондықтан - дің белгілі бір мәндерінде хаостың пайда болатын байқауымызға болады. Осындай шешімге 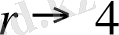кезінде (1.1) теңдеуіміз белгісіздік шешімге (хаос) ие болатындығынан байқауымызға болады. 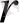күшейту коэффицентінің әр түрлі мәнінде генератордың жұмысын зерттеу барысында хаос пайда болатын 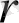коэффицентінің теориялық мәліметтерімен келісімді болатын жақсы нәтижелер алынған. Қарастырылған генераторда хаосты тербелістер 3.05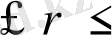3.97 мәнінде пайда болды. Теорилық анализ жасаған кезде логистикалық бейнелеудің хаосқа өтуі 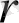- дің 3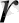4 мәнінде жүзеге асады.

2. Лоренц генераторы және оның сұлбасы

Үздіксіз диссипативті динамикалық жүйенің фазалық аумағында жабсырылған бифуркацияның негізгі элементі болып бір өлшемді тұрақсыз коллектор типті ұяшыққа ие болатын теңдік болып табылады. Біз келесі, симметрияға ие болатын, коллектордың екі әр түрлі компонентін бір-біріне түрлендіретін Лоренц теңдеуі сияқты жүйені қарастырамыз. Егер жүйенің параметрі өзгерсе, фазалық кеңістікте инвариантты коллектордың да орналасуы да өзгереді. Параметрлердің кейбір комбинацияларында тұрақсыз коллектордың компоненттерінің бірі тұрақты коллектордың ұяшығынан қашық орынға қайта келе алады және гомоклиникалық орбитаны құрастыра алады. Симметрия екінші компонентті қайта келуіне кепілдік береді: гомоклиникалық орбиталар жұп түрінде келеді. Гомоклиникалық орбитаның пайда болуы мен жоғалуын қамтамасыз ететін кезектілік жағдайлар бастапқы меншікті мәнге тәуелді. Сипатталған жағдайда тек қана бір меншікті мән бар, ол 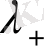деп белгіленеді. Нөлге жақын меншікті мәні- 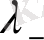шынайы болып табылады. "Ұяшық индексі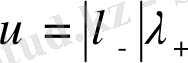"- қысқарту немесе кеңейту деген екі қасиеттердің қайсысы тұрақты нүкте аумағында фазалық кеңістікті басқаратынын көрсетеді. Егер симметрия болмаса, онда жалғыз гомоклиникалық траекторияның бұзылуы υ1 болғанда тұрақты және қарама-қарсы жағдайда тұрақсыз [5-6] болып келетін ерекше периодты орбитаны тудырады. Екінші жағдайда симметриялық гомоклиникалық траектория динамиканы құнарландырады : ұяшық аумағын қалдырып кететін барлық траекториялар қайтадан инжекцияланады. Бұл жағдайда 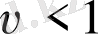тұрақсыз периодты орбитаның саналатын бөлігі, сонымен қоса ағымдағы траекторияның жалғасуы бір уақытта екі гомоклиникалық орбитадан туады : ол "гомоклиникалық жарылыс" [7]- ол алдағы Лоренц аттракторы жайлы маңызды мәлімет болып табылады. 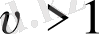жағдайы үшін қарапайымырақ: мұнда екі тұрақты периодты орбиталар ұяшық нүктесіне жақындайды және гомоклиникалық орбитаны құрап бірігеді. Екі гомоклиникалық траекториялар ажырағанда жаңа тұрақты симметриялы орбита фазалық кеңістікті қалдырады: ол алдын құрамында болған құраушылардың бірігуінен алынды. Траекториядағы ілгектердің (айналымдар) ұзындығы мен саны фазалық кеңістікте бифуркация жағдайында периодтың екі еселенуі сияқты екі еселенеді. Бұған қарама- қарсы жағдайда жүйе бифуркацияға жақындағанда уақытша периодтың мәні шектеусіз өлшемге дейін барады, гомоклиниклаық траектория жинақталып формаланғанда шексіз күйге ие болады. Ендігі параметрдің өзгеруі екіншілік біріккен бифуркацияның тізбектелуіне алып келеді: тұрақсыз коллектор фазалық кеңістікте бірнеше қосылудан кейін ұяшыққа қайта келеді. Оған дейін симметрияның бөлігі келесі аумақты алуы керек: жаңа пайда болған симметриялық периодты орбита бифуркацияның бағытына қарай тұрақсыздандырады және өзара симметриялы екі орбита одан екі еселенеді. Бұл екі орбита ұяшықтағы тұрақсыз коллекторға жақындайды және бифуркацияның келесі бірігуінде қосылады. Салдар сияқты, бастапқысынан 4 есеге көп ілгектері бар жаңа тұрақты периодты орбита пайда болады. Кезекті құбылыс бифуркацияның бірігуінен және симметриялы ажыраудың кезектесуінен тұрады, екі жапырақ формасына ие болатын Лоренц аттракторын еске түсіретін хаосты аттрактордың құрылуымен аяқталады. Бифуркация құбылысының соңында пайда болатын аттрактор тәртіп пен хаос арасында белгілі бір аралық орынға ие: траекторияның Фурье спектрі үздіксіз динамиканың жағдайындағыдай дискретті емес, хаосты немесе стохасты процесстегідей абсолютті үздіксіз емес, бірақ кері курсивті теріммен қуатталады. Сәйкесінше бақыланатын құбылыстар автокорреляциялық функцияның үлкен қашықтықтары арқылы сиппатталады. Егер құраушылар арасындағы симметрия тұрақсыз болса коллектор бұзылады.
Электронды сұлба бойынша динамикалық жүйені эксперименталды модельдеу теңдеудің қарапайым құрылымына ие болуы керек. Бифуркацияның бірігу тізбектілігі Лоренц теңдігі сияқты үш өлшемді фазалық кеңістікте пайда болуы мүмкін. Лоренц теңдеуі негізінен қажетті симметрияға ие. Лоренц теңдеуінің үш өлшемді параметр аумағында екі симметриялы гомоклиникалық орбиталардың құрылуы бірөлшемді болады: ол екі өлшемді бетке орналастыруды қабылдайды. Бұл бағытта теориялық тәжірибе жайлы жақсы зерттелмеген, бірақ сандық практикадан бифуркацияның барлық беті параметр кеңістігінің бөлігінде жатқанын байқаймыз. Бұл бөгеуден өту үшін қосымша параметр еңгізіп, бірнеше теңдеулерді қарастырамыз [5]

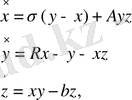(2.1)

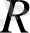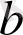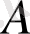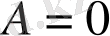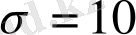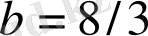мұндағы , және қарапайым Лоренц параметрлері болып табылады, сондай-ақ бірінші теңдеуге деген қосымша бейсызық термин еңгізіледі. болғанда (2.1) теңдеу Лоренц теңдеуіне айналады. (2.1) теңдеу жүйесі [8] жылулық конвекцияны зерттеу үшін сұйықтықтың қабаты үлкен жиілікті модуляцияға ұшырайтын модельді еске түсіреді. және параметрлерін [9] белгілеп аламыз және қалған параметрлер де өзгереді. (2.1) теңдеудің құрамында біз тек бифуркацияның бірігуіне және эксперименталды модельдеуге қатыстыларын ғана бөліп аламыз. (2.1) теңдеу 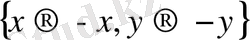түрлендіруінің қатысымен инвариантты. 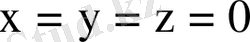теңдігі 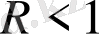үшін және параметрдің 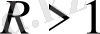диапозонында бір өлшемді тұрақсыз коллекторлы ұяшық үшін тұрақты болады. 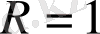болғанда бифуркация аумағы нөлдік аумақта болады. Мұндай екіге бөліну 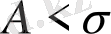үшін шекті мән болып табылады. Бастапқы Лоренц теңдеулеріндей параметрлердің өзгеруі ұяшықта тұрақсыз гомоклиникалық орбиталардың пайда болуына әкелуі мүмкін, бұл орбиталар 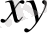жазықтығын тастап шығады және 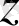- осьіне қайтып оралады.

Сурет 2.1. (2.1)-теңдеуді сипаттайтын негізі электронды сұлба [5]

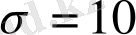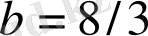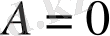
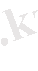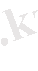
, , болғанда,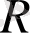=13.926 тең болады. Ұяшық индексі келесіге тең болады.

υ = 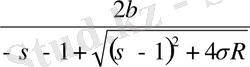(2.2)

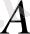мәні тәуелсіз болғандықтан, 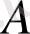- ның өзгеруі қосымша бейсызықтылықтың әсерін зерттеуге мүмкіндік береді. 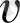мәні 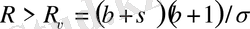үшін (2.1) теңдеуге қарағанда кіші болады және қарсы жағдайда (2.1) теңдеуден үлкен болады. Сандық интегралдау гомоклиникалық 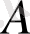- ның өсуі орбиталарды құрастыру үшін қажетті 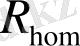критикалық мәнін төмендететінін көрсетеді. Осы арқылы, 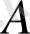- ның кіші оң мәні гомоклиникалық орбитаны бөледі, ол гомоклиникалық жарылыс болып табылады және Лоренц теңдеуінің хаосқа өтуі арқылы жүзеге асады, және 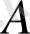- ның жеткілікті үлкен мәні (2.1) теңсіздігін қамтамасыз етеді.
Алдағы жасалатын өлшемдер үшін Лоренц аттракторының динамикасын қолдану арқылы электронды сызбамызға өзгерістер еңгіздік: (2.1) теңдеудегі бейсызық элементті ескере отырып қосымша аналогты күшейткішті сызбаға қостық. (2.1) теңдеуде келтірілген 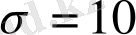және 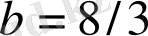электрлік сипаттамалар сәйкесінше тұрақты болады. 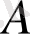және 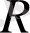параметрлерінің өзгеруі сәйкесінш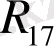е және 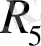кедергілерін өзгерту арқылы жүзеге асады. 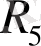- тегі 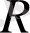- дің мәні 0,01 кОм- ға тең. Тізбектегі барлық кернеу динамикалық күшейткіштің жұмыс диапозонында қалатынына көз жеткізу үшін (-10- нан 10- ға дейін) тәуелді және тәуелсіз айнымалылар қайта өлшенуі керек: шексіз 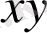және 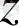потенциалдар айырымы вольтпен өлшенеді және 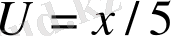, , 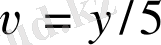болғанда жүзеге асады деп болжамдаймыз. 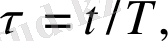Секундпен өлшенетін уақыт үшін 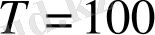еңгіземіз. Бұл өзгертулер келесі теңдеулерде байқалады [10].

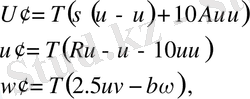(2.3)

мұндағы штрих бойынша дифференциалдау дегенді білдіреді. Соңында, күшейткіштің құрамында бейсызықтылықтың болуы, шын мәнінде және 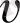мәндерінің бір уақытта ауысуына қатысты (2.3) теңдеуде идеалды симметрияны байқатпайтынын атап өту керек.

2.1 Тәжірибе нәтижелері

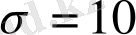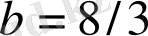және тұрақты болғанда тізбектегі уақыт бойынша тұрақты потенциалдар айырымын 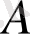және 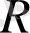- дың әр түрлі мәні үшін өлшеп, жаздық. 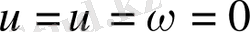теңдігі 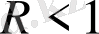үшін тұрақты және 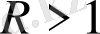диапозонында өзгереді. (2.1) теңдеуге қатысты тізбекті өлшеулер мен теңдеуді сандық интегралдау- негізгі гомоклиникалық орбиталарға ие 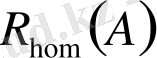қисығының бар екенін дәлелдейді. Тәжірибеде бұл жағдай асимтотада басқарылатын бастапқы шартқа қатысты өзгертілетіні белгіленген (сурет 2.2).

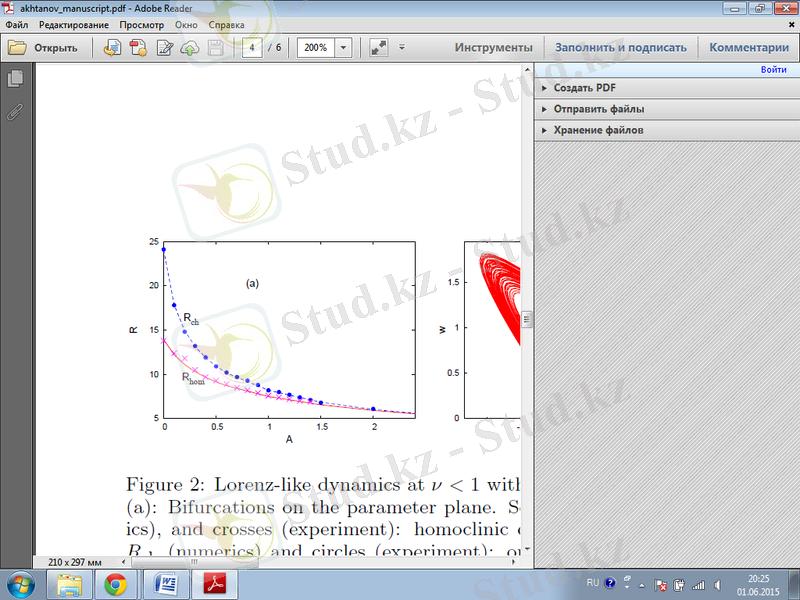
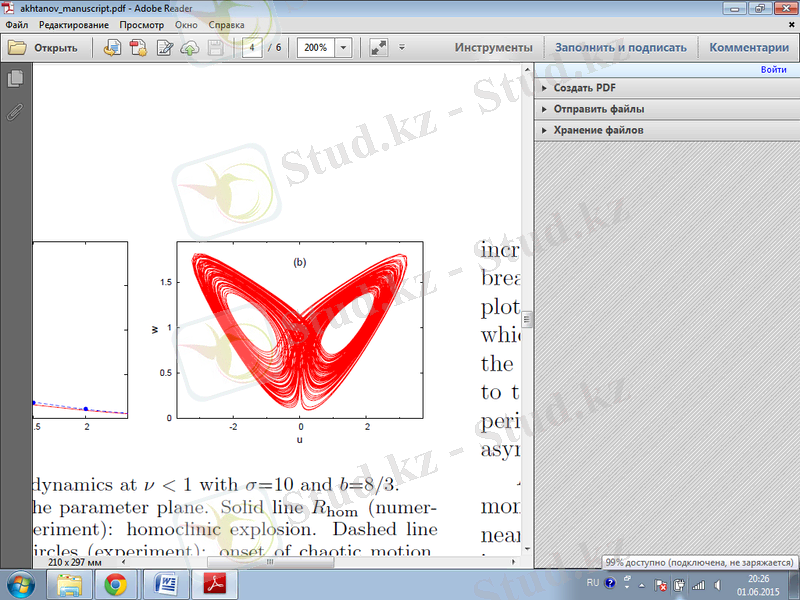
Сурет 2.2. 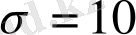және 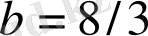тең болғанда, 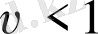мәніндегі динамика секілді Лоренц. а: параметр жазығындағы бифуркация. Түзу сызық 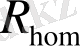және кресттер (эксперимент): гомоклиникалық жарылыс. Оң жақтағы үзік сызық 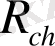және айналымдар (эксперимент): хаосты қозғалыстың басталуы; b: 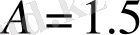үшін фазалық портреттің проекциясы (эксперимент) [5]

- ның төмен мәнінде гомоклиникалық орбитаны формалау мәнінде жүзеге асады, бұл Лоренцтің хаосқа өту процессіне сәйкес келеді. Шын мәнінде мәнін тұрақты етіп және мәнін жеткілікті түрде өсіру арқылы фазалық портреті Лоренц аттракторын еске түсіретін біз кернеудің ретсіз тербелісін байқадық (2.2-сурет). Жоғарыдағы тұжырымдарға қатысты гомоклиникалық жарылыстар сәйкес - дің мәні мәніне дейін төмендегенде бифуркациялық бірігумен ауыстырылуы керек, бұл диапозонына сәйкес келеді. Шын мәнінде Лоренц тәжірибесі мәнінде хаосты аттрактор сияқты және мәнінде біріккен бифуркация сияқты болатынын байқадық. Бифуркациялық процесс бойынша фазалық портреттің құрылуын жасап шығардық.

Сурет 2.3. Тізбектің негізгі жабсырылу бифуркациясы: Процесс жүруінің этаптары. Параметрлердің мәндері:
а: екі тұрақты периодты орбиталар; b: ; екі тұрақты периодты орбиталар; с: екі траекторияның құрылуы; d: тұрақты, өздігінен симметриялы орбита [5]

Бастапқы шартты өзгерте отырып, бір-біріне қатысты симметрияға жақын бір-екі тұйық траектория сұлбасының ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.