Бинарлы газ қоспаларындағы диффузиялық орнықсыздық

Пән: Химия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ

: 1

КІРІСПЕ: Бинарлы газ қоспаларындағы диффузиялық орнықсыздық

4: 5

: 1. 1

КІРІСПЕ: Қос диффузия

4: 5

: 1. 2

КІРІСПЕ: Газдардағы диффузиялық орнықсыздық

4: 8

: 1. 3

КІРІСПЕ: Бинарлы газ қоспаларындағы квазистационар жағдай үшін диффузиялық және конвективтік араласу процесінің сипаттамасы

4: 10

: 1. 4

КІРІСПЕ: Газ қоспаларындағы механикалық тепе-теңдік орнықсыздығының жалпы теңдеулері

4: 16

: 2

КІРІСПЕ: механикалық тепе-теңдіктің бұзылуын ТӘЖІРИБЕЛ1К ЗЕРТТЕУ

4: 22

: 2. 1

КІРІСПЕ: Екіколбалық әдіс

4: 22

: 2. 2

КІРІСПЕ: Араласу процесінің визулизациясы

4: 24

: 2. 3

КІРІСПЕ: Газ қоспаларының концентрациясын интерферометрмен және хроматографпен өлшеу

4: 27

: 2. 4

КІРІСПЕ: Храматограф көмегімен газ қоспаларының концентрациясын өлшеу

4: 28

: 2. 5

КІРІСПЕ: Өлшеу қателіктері

4: 30

: 3

КІРІСПЕ: Әртүрлі қысымдар үшін изотерімдік жағдайдағы диффузиялық орнықсыздықты математикалық модельдеу

4: 32

: 3. 1

КІРІСПЕ: Изотерімдік жағдайдағы диффузиялық орнықсыздық процессіне қысымның әсері

4: 32

: 3. 2

КІРІСПЕ: Бинарлы газ қоспаларындағы изотерімдік диффузияның негізгі теңдеулер жүйесі. Есептің қойылымы

4: 34

: 3. 3

КІРІСПЕ: Негізгі теңдеулер жүйесін сандық шешу

4: 37

: 3. 4

КІРІСПЕ: Математикалық модельдеу әдісінің нәтижелері

4: 44

КІРІСПЕ: ҚОРЫТЫНДЫ

4: 48

КІРІСПЕ: ҚОЛДАНЫЛҒАН ӘДЕБИЕТ ТЕР ТІЗІМІ

4: 49

Кіріспе

Көпкомпонентті газ тасымалдауының практикалық тапсырмаларын шешу кезінде жиі қарастырылатын ерекше жағдай, бұл-көп компонентті зат тасымалының гидродинамикалық құрамын бөлуге мүмкіндік беретін жылжымайтын газдардың (газ-сұйылғыш) қабаттары арқылы жүретін екі немесе бірнеше газдардың диффузиясы.

Әр түрлі көпкомпонентті қоспалармен байланысты табиғи және технологиялық процестерді қарастырғанда, біз оның негізгі масса тасымалдауын ерекшеліктерін көрсететін параметрлерді білуіміз қажет. Нақты кездесетін заттар мен құбылыстар алуан түрлі, сондықтан олардың массатасымалдауын анықтайтын коэффициенттер мәндері де әртүрлі және олар өте кең зерттеулерді талап етеді. Қазіргі уақытта көпкомпонентті қоспалардағы диффузия құбылысы алдағы уақытта әлі де терең зерттеулерді талап етеді. Оған мысал ретінде соңғы уақыттардан бері терең зерттелініп келе жатқан изотермдік үшкомпонентті газ қоспаларының диффузиясы кезінде пайда болатын механикалық тепе-теңдіктің орнықсыздығының байқалуын айтуға болады. Гидродинамикалық ағыстың диффузиялық ағысқа қосылуы әртүрлі бароэффект, керідиффузия, диффузиялық бөгет сияқты эффектілерге әкеледі, ол эффектілер тәжірибе жүзінде тұйықталған екі колбалық жүйе әдісімен зерттеледі [1] .

Көптеген технологиялық схемаларды зат алмасу процесінде маңызды рөлді диффузия атқарады, мысалы: табиғи газдан аммиакты синтездеу, газ тәрізді отынның жануы. Қазіргі уақытта химиялық технологиялардың, ракеталық және авиакосмостық техникалардың өнеркәсіптік аппараттарын жасау және есептеу кезіндегі бинарлық қоспа жағдайына арналған зат тасымалдау тұрақтысы туралы білім жеткіліксіз. Зерттеу жұмыстары жабық жүйелердегі диффузия процесінің күрделі құбылыс екенін көрсетеді. Газ қоспаларының диффузияланып жатқан молекулаларының бірдей емес шапшаң қозғалысы салдарынан жабық диффузиялық аспаптардағы қысымның күрт төмендеуінің пайда болуы тұтас түрдегі газ қоспаларының гидродинамикалық ағымының пайда болуына алып келеді. Компоненттердің жалпы (жинақтық) тасымалын диффузиялық ағымдарға бөліктеу және диффузия процесінің дұрыс диффузиялық бейнесін гидродинамикалық түрде беру тек екі компонентке ғана емес, одан да көп күделі қоспаларға да арналған.

Массатасымалдау процестерін моделдеу - табиғи газдарды тазарту, бөлу, газ қоспаларын белгілі компоненттермен толықтыру - қазіргі ғылымның жаңа бағыты болып отыр. Аталған процестерде көпкомпонентті газ қоспаларыының араласуында тек молекулалық тасымалдау ғана емес конвективті тасымалдауда орын алатыны белгілі.

1 Бинарлы газ қоспаларындағы диффузиялық орнықсыздық

1. 1 Қос диффузия

50-ші жылдардың ортасында "тұз фотондары" атты мұхитты графикалық зерттеулер кезінде ‹‹қос диффузиялы конвекция›› ("double diffusive convection") немесе ‹‹қос диффузия›› атты құбылыстар анықталды [1] . Мына әдебиеттерде [2-3], қазіргі уақытта қос диффузия процессі деп сипаттауға болатын құбылыстар көрсетіледі. Алайда ол кезде бақыланып отырған құбылысқа физикалық сипаттама берілмеген еді. ‹‹Бұл жұмыстың дамуы сұйық механикасының басқа облыстарына қарағанда қарқынды болмады. Бұл мұхитты графикалық ұйымдардың аз болуымен және тәжіребелік жұмыстардың болмауымен байланысты болатын.

Алғаш рет диффузиялық процесте орнықсыздықтың пайда болуын Миллер мен Мейсон үшкомпонентті газды қоспада термоэффектті зерттеу кезінде анықтаған болатын [5] . Лошмидтің диффузиялық аппаратында тәжірибелі тіркелген температура өзгерісі, газдардың бөліну шекарасына жақын жүйелер үшін тұрақсыз тербелістер күйінде көрінеді. Бірақ бірсарынды ұлғаюы болуы керек еді. Диффузиялық араласу кезінде газ қоспаларының осындай болуы, жүйенің концентрациялы орнықсыздығынан туындаған қоспаның (құрамының) тығыздық осциляциясымен түсіндіріледі. Жұмыстың авторлары өздерінің тәжірибелерінің нәтижелерінен газды қоспа компоненттерінің аномальды болуына жалпы физикалық түсініктеме береді және кейінгі басылымдарында осы сұрақты талдап көрсетеді [6] . Алайда, изотерімді көп компонентті диффузия кезінде конвективті ағындардың пайда болуы көрсетілмеді.

Көпкомпенентті газдардағы диффузия кезінде компоненттер концентрациясының тұтрақсыз тербелістері көрсетілген.

Өткен ғасырдың 60-шы жылдарынан бастап профессор Н. Д. Косовтың басқаруымен С. М. Киров атындағы ҚазМУ "жылуалмасу жане жану" лабаратория қызметкерлері көпкомпенентті газды қоспаларда диффузиялық процестерді зерттеуге кірісті. Жұмыстың мақсаты көпкомпонентті массатасымалдану процессі мен эффекттерді, диффузия коэффициенттерін есептеу әдісін жасау мен өлшеулер жүргізу болды. Тәжірибелер жүргізу кезінде екі колбалы диффузиялық аппаратта (квазистатционарлы диффузия), аппараттың жоғарғы колбасында ${0. 5\ Н}_{е} + 0, 5А_{r}$ бинарлы қоспа орналасқан, жоғарғы қысым кезінде $р\sim 1, 0 \div 1, 5$ МПа диффузиялық ағыннан бірнеше рет басым болатын конвективті ағындардың пайда болуы анықталады [8] . Конвекцияның пайда болуын белгілі "Тур эффекттерімен" [9; 10] немесе диффузиялық бароэффекттің әсерінен пайда болған гидродинамикалық ағынмен түсіндіруге болады [11] .

Бұл ағындардың пайда болуын байланыстыру газды қоспаларының идеалдықтан ауытқымауын және олардың нақты қасиеттерін көрсетумен дәлелді түсініктеме алмады, себебі қысымның сол аймағында ( $1. 0 \div 1, 5$ МПа), онда конвекция әсері ерекше елеулі болған таза газдар және олардың қоспалары $\ 2 - 3\ \%\$ аспайтын қателігімен Менделеев-Клайперон тендеуімен сипатталады.

Мұхитта жылудың, тұздың және энергияның тасымалдануы тасымалданудың турбулентті коэффициенттерімен сипатталады. Сондықтан терең мұхитта турбулентті араласу басым болуы керек деп есептеледі. Осының әсерінен температураның градиенті елеусіз және бір-бірінен алыста таралған баромерлік бөтелкелердегі су сыналарымен дәлелденген. 60-шы жылдардың ортасында табиғи зерттеулердің нәтижелері көрінді. Бұл тығыздық және температурасының флуктуациясының терең өзгеруін үздіксіз өлшейтін жаңа құралдардың пайда болуымен байланысты. Өлшеулердің көрсетуі бойынша тұздылық және температура пішіні әрдайым тегіс болмайды, көбінесе жылдам өзгеретін градиент бөліктерінен тұрады. Калифорния жағасында алынған температура, тұздылық және тығыздық пішіндері 1-суретте көрсетілген [12] .

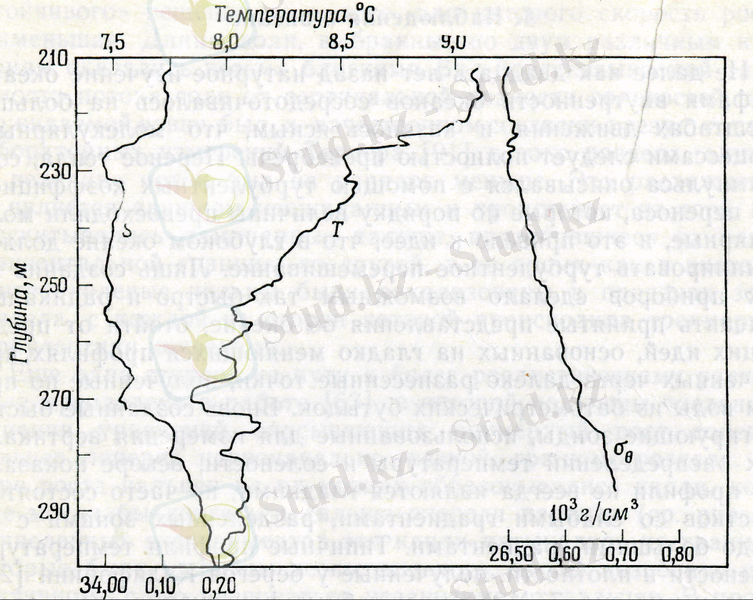
Сурет 1. Теңіз суының тұздылығының және тығыздығының температурасының профилі

Федоров К. Н и Стоммел Х. қабаттардағы диссипацияның ықтимал уақытша масштабын және жылдамдығын бағалады. Температура өзгеруінің және тұздылығының өзара әсер етуі оларды градиенттерінің инверсиясын туғызуы мүмкін [13] . Олардың болжамы бойынша ‹‹қос диффузия коэффициенті кезінде конвекцияның әртүрлі түрін көрсетеді››. 1997 жылы инжинер-океаналог Уильмис арнаулы көлеңкеленген құралдың көмегімен Жерорта теңізі және Террнес теңізі ағысынан тұз саусақтарын тапты [14] . Егер тұздылығымен және температура айырымдарымен бірін-бірі компенсациялайтын қабат ‹‹сол тығыздықты күшті қасиетері бар›› сұйықтықпен қоршалған болса, қос диффузиялы конвекция үшін қолайлы шарттар кездесетінін бақылаудан көреміз. Егер орташа үлестірулер аномальды конвекцияның пайда болуына алып келмесе де, мысалы, Тынық мұхитының көп бөлігінде болса, онда аз температура градиенті және тұздылығы тұрақты болады. Горизонталь фулктуациялар вертикаль фулктуацияларды өзгеруінен қос диффузиямен жасайтын процестер жұмыс істеп бастауы мүмкін.

Егер температурасы тұздылығы бойынша үлкен горизонталь қарама-қарсы болса, бірақ тығыздықтың қорытынды айырмы аз болғанда күшті қабаттасу байқалады. Грегг интенсивтілігі фронттан алыстаумен азаятын инверсияларды тапты [15] . Осы бақылаулардан Хапперт пен Тернер ‹‹молекулалық эффекттер тек қабат масштабындағы қозғалыстарға ғана әсер етпейді [4], яғни вертикаль бойынша он шақты метр, су массалар арасындағы үлкен масштабты араласуында маңызды рөл ойнауы мүмкін››.

[16, 17] жұмыстарында қос диффузия конвекция терминдерін түсіндіргенде жер атмосферасында және үлкен жұлдыздарда болатын атмосфералық құбылыстардың және процестердің массалары келтірілген. Ылғал ауаның масса көтерілуінің радиолокациялық бақылауларының көрсетуі бойынша жылы, құрғақ ауамен ылғал, суық ауа арасында кенет шекара байқалады [16] . Яғни суық ауаның жылы ауадан ылғал қабаттың пайда болуы, суық ауаның суық фронт айналасынан пайда болу жағдайы байқалады. Ылғалдылық және температура грдиенті бір-біріне қарама-қарсы бағытталған. Осындай таралу кезінде ылғал ауаның потенциалдық энергиясы қос диффузия конвекцясы бөлу шекарасын ұзақ ұстай алады. Бірақ қандайда бір әсерден бұл тепе-теңдік бұзылуы мүмкін, ол қуатты конвективті массатасымалдануына алып келеді.

Үлкен жұлдыздар ядрода жиналған гелиймен бай, ал ядроның сыртында жеңіл сутегі басым болады. [17] жұмыста химиялық құрамының градиенті, гелий-сутегі тығыздық градиентін туғызады және төменнен қыздыру орны бар гелий синтезі энергия бөлумен болады. Қос диффузия конвекциясы көмегімен жоғарыға гелий тасымалданатын конвнективті қозғалыс пайда болады. Осындай күйде тығыздық градиенті тұрақты болғанда температура таралуы біртекті болады. Астрофизикалық орнықсыздықтың басқа ерекшелігі жұлдыздың айналуының бұрыштық моментінің және температура градиентінің таралуы болып келеді. Осындай жүйеде дифференциалды айналудан энергия іріктеуімен орнықсыздық дамуы мүмкін. Ол бұрыш моментінің таралуында орнықсыздық тудырады.

Жанартау атқылағанда бақыланатын теңіз түбінде болған жағдай ерекше қызығушылық тудырады. Мұхит түбінде өте ыстық және тұзды сұйықтың суық суда ағып шығу кезінде осы ағынның екі бөлікке бөлінуі бақыланып біріншісі жоғарыға көтеріледі, ол ыстық және онша тұзды емес. Екіншісі жылы теңіз суымен байытылған ағыс көрсетілген бақылау шекарасымен мұхит түбімен жайылып жатыр. Уақыт өте келе кристаллизация болады және мұхит түбінде қалған құрамның тұнуы бірнеше километрге горизонталь созылады жатыр. 2-суретте осындай процестің кесіндісі келтірілген [18] .

Сурет 2. Жанартаудың интрузиясының түрлі тығыздық қабаттары

Қабаттардың тұрақтылығы қос диффузия құбылысының әсерінен сұйық күйде пайда боғанын көрсетеді. Гидродинамик Хапперт және геолог Спаркстың болжамы бойынша [19] қабаттың пайда болуына жаңа магманың периодты құйылуы себепші болады. Ол құрамның айырмашылығына байланысты ағып кеткен магмаға қарағанда жылылау болады және оған қарағанда ыстық болуы мүмкін. Жаңа магма қабат тудырады, жоғары жатқан бөлу шекарасынан жылуалмасу арқасында суып қалады. Қабат жоғарыдан суый бастайды шекара үстінен зат тасымалдауы елеусіз болады, сондықтан оның ішінде оливин кристаллдары пайда болады. Жаңа және ескі магмалар қабаттарының арасында жылулық тепе-теңдік басталғанда кирсталлдар түсіп қалады да, қалған сұйықтықтың тығыздығы температура кемейуімен азаяды. Ол мұхит суының жоғарғы қабатымен араласып жоғарыға көтерілуі мүмкін.

1. 2 Газдардағы диффузиялық орнықсыздық

Изотерімді үшкомпонентті газды қоспаларда диффузияны тәжәрибелік зерттеулер, олардың кейбіреулерінде белгілі шарттарда құрылымды конвективті ағындар пайда болып және олардың өзінің молекулалық тасымалдануына әсер етуі қоспаның диффузиялық орнықсыздығына (механикалық тепе-теңдік орнықсыздығы) алып келетінін көрсетті [21-22] . Диффузиялық каналда араластын газдардан тұратын конвективті ағындардың пайда болуы үшін тығыздықтыры әртүрлі екі қабат асты құрылуы керек. Тығыздығы үлкен қабат асты тығыздығы аз қабат астының үстінде орналасуы қажет. Қабат астыларының ауырлық күші өрісінде осылай орналасуы орнықсыз және кез-келген қозғалыстан орын ауыстыруы мүмкін. Сонда өте ауыр қоспа төменге ағады, ал өте жеңіл қоспа жоғарыға көтерілуге тырысады, яғни ковекция пайда болады. Бастапқы құрылған өте ауыр қоспа жеңіл қоспаға ‹‹бұрқ етуі›› де болады. 3-суретте мысал ретінде диффузиялық каналда және диффузиялық аппарат колбасында диффузиялық орнықсыздығының көлеңкеленген суреттері көрсетілген [21] .

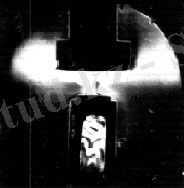
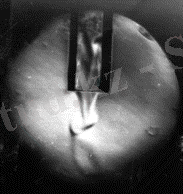
а) б)

а, б диффузиялық аппараттың төменгі және жоғарғы колбасы.

Сурет 3. $0. 5143He + 0. 485CO2$ кезінде $p = 1. 5$ Па жүйесінде диффузиялық орнықсыздық процесінің көлеңкеленген суреттері, $T = 298$ К

Диффузиялық каналдың аймағында құрылымды конвективті ағындар анық көрінеді. Жоғарғы колбада диффузиялық каналды жабатын қақпақ көрінеді. Ерікті гравитациялы концентрациялы конвекцияның пайда болу себебі араласу түрін табумен, орнықсыздықтың сызықты теориясымен түсіндірілген [23; 24]

Алынған нәтижелер физикалық мағынасы бойынша жылулық конвекция кезінде орнықтылықтың бұзылуымен байланысты [23] . Бір режимнен екінші режимге ауысу шекарасын анықтауға мүмкіндік береді [24] . Изотерімді көпкомпонентті жүйелер үшін орнықтылық диффузия облысының бірсарынды және тербелмелі орнықсыздық болуы көрсетілген. Геометриясы әртүрлі каналда орналасқан кейбір газ қоспаларының орнықтылық негізіндегі теорияларына сәйкес келетін тәжірибе мәліметтерімен дұрыс салыстыруға мүмкіндік береді.

Кейбір газды қоспаларда диффузиялық орнықсыздықты зерттеу кезінде диффузиялық процестің пайда болуына және ауысу түріне әртүрлі факторлар мен қоспа параметрлері әсер етеді. Осы кезде табылған эффекттерді ғылым және техника облысында қолдануға болады. Мысалы, газды қоспаларды анықталған компоненттермен байыту

1. 3 Бинарлы газ қоспаларындағы квазистационар жағдай үшін диффузиялық және конвективтік араласу процесінің сипаттамасы

Изотермдік жағдайдағы бинарлы газ қоспаларындағы өзара диффузияны сипаттау үшін Фик заңы деп аталатын келесі феноменологиялық қатынас қолданылатыны мәлім:

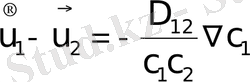, (1)

мұндағы, 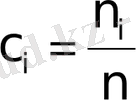, i - ші компоненттің мольдік үлесі, $\overrightarrow{u_{1}}$ - i -ші компоненттің орташа жылдамдығы, n _i - осы құрамдас бөліктің сандық тығыздығы, n = n ₁ + n ₂ - қоспаның сандық тығыздығы, $D_{12}$ - заттардың бірінің біреуіне өту жылдамдығын сипаттайтын өзара диффузия коэффициенті (ӨДК) .

$\overrightarrow{u_{1}}$ , $\overrightarrow{u_{1}}$ (2) табу үшін (1) формуласын байланыс теңдеуімен толтыру қажет [6; 7] .

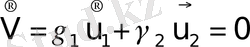, (2)

мұндағы, $\overrightarrow{V}$ - қоспаның қайсыбір сипаттамалық жылдамдығы, $\gamma_{1}$ , $\gamma_{2}$ - қайсы бір өлшемсіз коэффициенттері, сонымен қатар, $\gamma_{1} + \gamma_{2} = 1$ .

Өзара диффузия жағдайы кезінде жабық жүйелердегі идеал газ қоспалары үшін орташа сандық жылдамдыққа қолданылатын (2) шарт келесі түрде болады:

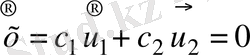, (3)

мұндағы 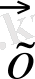- қоспаның орташа сандық жылдамдығы.

Өзара диффузия кезінде компоненттердің молекула массаларының және олардың эффективті көлденең қимасының әртүрлілігінен молекулалар әртүрлі жылдамдыққа ие болатындығын көрсеткен еді. Осының әсерінен құрылғы колбасындағы молекулалардың таралуы байқалады. Ең жеңіл және ең тез қозғалғыш молекулалар құрылғының колбаларын біріктіретін капилярдан кері қарай қозғалатын ауыр молекулаларға қарағанда жылдамырақ өтеді, яғни молекулалардың орын ауыстыруы өзгермейді. Осының әсерінен, колбалар арасында $\mathrm{\Delta}\ p$ қысым айырмасы пайда болады. Бұл құбылыс диффузиялық бароэффект деп аталады [8-11] . Дегенмен $\mathrm{\Delta}\ p$ құрылғы колбаларындағы қысымымен 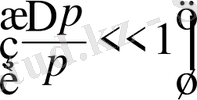салыстырғанда аз, бірақ тұтқыр режим жағдайында қысым айырымын тудыратын гидродинамикалық ағыстың жылдамдығы диффузиялық жылдамдықтармен шамалас. Сондықтан оны ескермеуге болмайды. $\mathrm{\Delta}p$ колбадағы қысым айырымы газдардың араласу уақытына баяу релаксацияланады [6] .

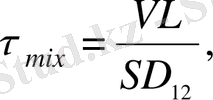
ол Кнудсеннің аз санынан Kn $< < 1$ колбалардағы қысым айырымының тұтқыр релаксация уақытынан көп болады [6-11] .

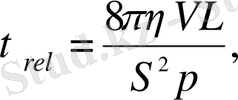
мұндағы $\eta$ - капиллярдағы қоспаның динамикалық тұтқырлығы.

Концентрация $\tau_{mix}$ және қысым $\tau_{rel}$ релаксация уақыт мәндері қатынасында Кнудсен ${Kn}^{2}$ $(Kn = \frac{\lambda}{d}, \$ мұндағы $\lambda$ - еркін жүру ұзындығы; $d$ - есептің өзіндік өлшемі) санының квадрат реті бар. Егер Kn $< < 1$ болса, онда $\tau_{rel} < < \tau_{mix}$ уақыт аралығында жабық жүйеде квазистационар диффузия режимі орнайды, сол кезде концентрацияның тиесілі градиенті астынан қысымның градиент аясын «құру» пайда бола бастайды. Одан кейін, араласу процесіндегі $\mathrm{\Delta}\ p$ өзгерісі $\tau_{mix}\$ уақытына сәйкес болады.

Қысым градиентінің баяу өзгеруін ескермей, квазистационарлық диффузияның шартын келесі түрде жазамыз:

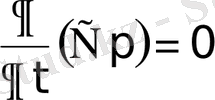. (4)

Радиусы r , ұзындығы L капиллярмен [12-15] жалғанған көлемдері бірдей екі колба жүйесі үшін бірқалыпты тасымалдау келесі түрде жазылады [6] :

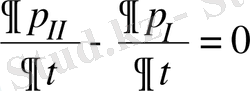Көлемдері $V_{I}$ , $V_{II}$ (4-сурет) екіколбалы тұйық жүйеде бөлшектердің санын сақтау шарты келесідей:

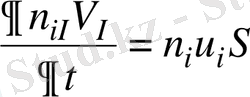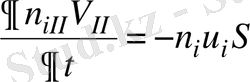, , (5)

мұндағы $V_{I}$ , $V_{II} - \$ сәйкесінше түрде төменгі және жоғарғы колбалардың көлемдері, $S = \pi r^{2}$ - диффузиялық каналдың көлденең қимасының ауданы.

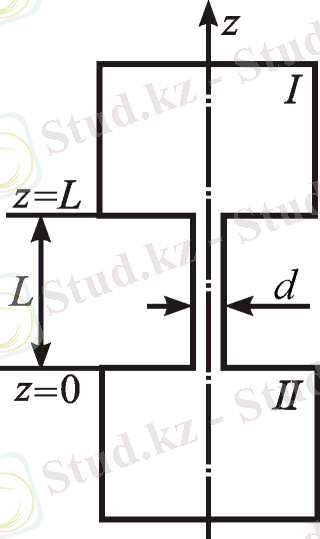
Сурет 4. Екіколбалы әдістің диффузиялы ұяшығы

(1), (3) және (5) теңдеулерін бірге шеше отырып, колбадағы концентрация айырмасының $t$ - араласу уақытынан тәуелділігін аламыз:

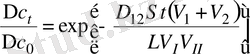. (6)

мұндағы $\mathrm{\Delta}c_{0\ } = c_{I}(0) - c_{II}(0)$ - бастапқы уақыт кезіндегі концентрация айырмасы, $\mathrm{\Delta}c_{t\ } = c_{I}(t) - c_{II}(t)$ - $t$ -уақыт кезіндегі концентрацияның айырмасы.

(6) теңдеуді Ней, Армистед және Эндрюмен бір-біріне тәуелсіз алған [13] .

Диффузиялық құрылғының колбаларындағы (тек каппилярда ғана емес) концентрацияның таралуын есепке алу үшін, яғни колбаның диффузиялық кедергісі үшін капиллярдың L геометриялық ұзындығынан оның эффективті мәніне $L_{эфф}$ өтуін жүзеге асыру керек [6] .

, (7)

мұндағы, $d - \$ капилляр диаметрі, $a = (0. 745 \pm 0. 012)$ .

Екіколбалық әдіс сиретілген газ үшін ғана емес, сондай-ақ температура мен қысымның үлкен интервалындағы тығыздалған газдарда диффузияны зерттеу кезінде де кеңінен қолданылады.

Диффузиялық бароэффекттің бар екеніне болжау жасаған Больцман [22] және Максвелл [23] болатын, бірақ алғаш бароэффектті 1943 жылы сутектің ауадағы диффузиясын зерттеу нәтижесінде Крамерс пен Кистемакер [24] өлшеген болатын. Тұтқыр және жылулық жылжу үшін жасаған Максвеллдің [23] есептеу әдісіне арқа сүйей отырып, Кнудсеннің кіші сандары үшін теориялық формуланы да осылар тапқан. Пуазейл ағысын ұстап тұратын ауыр газ қысымының градиенті орнағанда гидродинамикалық ағыс тұрақты болатыны болжанған еді.

Мұндағы өзара диффузия кезінде пайда болатын бароэффекттің мәні $\mathrm{\Delta}p,$ диффузиялық жылжуды ескеріп және ескермеген шарттарда алынған [24] :

$\mathrm{\Delta}p = \frac{4\overline{\eta}D_{12}}{r^{2}}\ln\frac{m_{2}}{m_{1}}$ (жылжуды ескере отырып)

$\mathrm{\Delta}p = \frac{8\overline{\eta}D_{12}}{r^{2}}\ln\frac{m_{2}}{m_{1}}$ (жылжуды есепке алмай)

мұндағы $\overline{\eta}$ - капиллярдың ұзындығымен орташаландырылған қоспаның тұтқырлық коэффициенті, $r$ - капилляр радиусы, $m_{1}{, \ \ \ m}_{2}\$ -диффундирленген газдардың молекулаларының массасы.

Диффузиялық бароэффектті зерттеу көрінісі кейіннен П. Е. Суетин мен П. В. Волобуевтің [8, 9] жұмыстарында жетілдірілді. Диффузиялық бароэффектті зерттеу үшін сезімталдығы жоғары сыйымды дифференциалды микроманометр құрастырылды. Олардың негізгі элементі тігінен орналасқан диаметрі 64 мм және қалыңдығы 0, 1 мм болатын бериллийлі қоладан жасалған екі гофрлы мембранадан тұрды. Қысым айырымының әсерінен мембраналардың бірі орын ауыстырылып, олардың арасындағы сыйымдылық өзгереді, мұны екінші аспап - сыйымдылықты жетілдіру өлшеуіші аспабымен өлшеуге болады.

Диффузиялық бароэффект каналдағы ағыс кезінде газдардың бөліну эффектісіне қарсы болып табылады [7] . Онзагердің арақатынастары арқылы бароэффекті зерттеу мембрананың айырғыш ерекшеліктерін анықтауға мүмкіндік береді.

Диффузиялық бароэффекті зерттеу басқа да маңызды ғылыми және практикалық мағыналарға ие. Сол себептен [7] жұмыста диффузиялық бароэффектің газдардың араласу уақытынан $\mathrm{\Delta}p(t)$ тәуелділігіне қатысты, $\frac{L}{R}$ және $K_{n}$ параметрлерінің кең көлемінде алынған тәжірибелі деректер келтіреді және талданады, сонымен қатар, қалпына келтіру әдістемесі ұсынылған, мәндері берілген және каналдағы газдардың бинарлық қоспасының қозғалысын сипаттайтын барлық үш кинетикалық LPP, LPD және LDD коэффициенттердің полуэмпириялық формулалары табылған.