Жасанды нейрондық жүйелер: нейрон моделі, активация функциялары, архитектуралар және MATLAB Neural Network Toolbox


Кіріспе
Соңғы уақытта нейрондық жүйелерде ұлкен қызығушылық байқалады. Ол көптеген салаларда қолданыс тапты: медицинада, бизнесте, техникада. Нейрондык жүйелерді басқару, болжау, классификация мәселелерін шешуде қолданылады.
Нейрожүйенің ерекшелігі, ол оқыту механизмінде (механизм обучения) қолданылады. Нейрондық жүйе қолданушысы өкілі деректерді таңдап және оқытылатын алгоритмдерді жібереді. Алгоритм өз бетімен параметрлерді қалыптастырады. Қолданушыға қойылатын негізгі талаптар, бұл - эвритистикалық біілімнің болуы, яғни деректерді дайындау, нейрондық жүйелердің архитектурасын таңдау. Алынған нәтижелерден қорытынды шығару. Айта кететін болсақ, қолданушыға нейрондық жүйе қолдану барысында қойылатын талаптар әлдеқайда аз болып келеді, мысал үшін дәстүрлі әдістерге қарағанда.
Дегенмен, жасанды нейрондық жүйе қарапайым нервтік жүйенің биологиялық моделі бойынша жасалынған.
Нейроннан алынатын сигналдың қарқыны байланыс сызығының белсенділігіне байланысты. Әрбір байланыс сызығының өзіне тән ұзндығы болады. Сол арқылы арнайы химиялық заттар сигнал жібереді.
Көп нейроннын тұрайтын ми өте қиын операцияларды жүзеге асыруға қабілетті. Дәл осындай модельді жасанды нейрондық жүйелер іске асырады. Жасанды нейрондық жүйе сонымен қатар өзара параллельді әрекет ететін қарапайым элементтерден құралған. Нейрондық жүйе функциялары табиғаттағыдай элементтер арасындағы байланыс бойынша анықталады. Байланыс коэффиценттерінің мәндерін өзгерте отырып, нейрондық жүйелерді белгілі бір функцияларды жүзеге асыру үшін оқытуға болады. Әдетте жасанды нейрондық жүйе белгілі бір нақты кірістер мақсатты шығыстарға айнлатындай етіп оқытады. Шығыс және мақсат сигналдарын бір біріне сәйкес келгенше салыстыру арқылы оқытылады.
Жасанды нейрондық жүйе негізінде интеллектуалды жүйелер, бейнелерді таңдауы, бақлаудың орындалуын, ассоциативті жады және басқалардың мәселелерін орындап келе жатыр.
ППП Neural Network Toolbox қолданушыларға проектілеу әдістерін дамыту және нейрондық жүйелерді қолдану аймағын кеңейту үшін қызмет ететін құрал.
Нейрондық жүйелер көптеген салаларда әр түрлі мәселелерді шешуде қолданылады:
- Космонавтика мен аэронавтикада
- Машина жинау
- Банк ісінде
- Әскери салада
- Электроникада
- Қаржы ісінде
- Сақтандыру саласында
- Өндірісте
- Медицинада
- Мұнайгаз өндірісінде
- Робототехникада
- Деректер жіберуде
Нейрон моделі
- Қарапайым нейрон
Нейрондық жүйе қарапайым ұяшығы болып нейрон болып табылады. Бір скалярлы кірісті нейронның құрылысы 1. 1, а. суретте көрсетілген
1. 1 сурет
Скалярлы кіріс p сигналы скалярлы w аймақты коэффицентіне көбейтіледі, нәтижесінде шығатын өлшенген кіріс W x P нейрон активациясы функциясының аргументі болболсаып табылады. Сөйтіп а скалярлы шығысты тудырады.
1. 1, в суретінде көрсетіген скалярлы жылжу өлшенген кіріс W x P арқылы есептеледі және f функциясының аргументінің b шамасына жылжуына алып келеді.
Егер нейронның мәні 1-ге тең болатын екінші кіріс сигналы бар болса, жылжу әрекетін салыстыру схемасына сәйкстендіруге болады.
Кірістің нейрон активация n функциясы сол қалпында скалярлы болып қалады, сонымен қатар салыстыру кірісі мен b ығысу шамасының қосындысына тең болады. Ол f активация функциясының аргументі болып табылады. Ал шығыс функциясының активация а сигналы болып табылады. W және b тұрақтылары нейронның скалярлы параметрлері болып есептеледі. Нейрондық желілер негізгі принципі нейрон параметрлерін өзгерту арқылы жүйенің нақты жұмыс атқаруына оқытуға болады. Сонымен қатар жүйенің өзін-өзі жөндейтіндей етіп үйретуге болады.
Нейрондардың жылжу теңдеуі:
(1. 1)
Жоғарыда көрсетіле кеткендей b жылжуы - нейронныңкіріс болып табылмайтын скалярлы параметрі, ал мұндағы 1-тұрақтысы кіріс болып табылады және жылжуды басқарады
1. 2. Активация функциясы
Нейронның активация функциясы әр түрлі болады. F активация функциясы n аргументі және а шығысты сигмоидальді функция тобына кіреді.
Кең таралған функция активациясының 3 түрлі формасын қарастырайық. Hardlim қатал шектеулі функция активациясы. Бұл функция а = hardlim(n) = 1(n) қатынасын сипаттайды және ол 2. 2 суретте көрсетілген. Егер n<0 ол 0-ге тең, ал n>0, онда 1-ге тең.
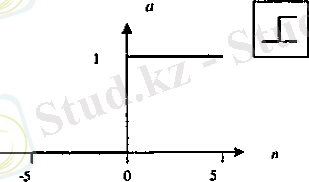 2. 2 сурет
2. 2 сурет
ППП Neural Network Toolbox құрамына қатал шектеулі функция активациясн жүзеге асыратын hardlim M-функциясы кіреді. Операторларды Matlab тілінде
қолдана отырып, омы функцияның графигін құрастыруға болады.
n = -5:0. 1:5;
plot(n, hardlim(n), 'c+:') ;
Нәтижесінде -5тен +5ке дейінгі мәндер арасында hardlim функциясының графигін аламыз. (сур. 1. 2)
Purelin сызықты активация функциясы. Бұл функция а = purelin(n) =n байланысын сипаттайды. (сур. 1, 3)
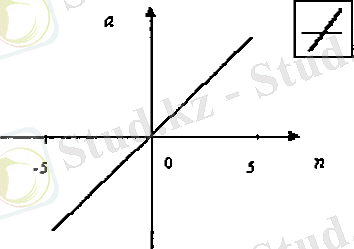 сурет 1. 3
сурет 1. 3
Logsig логистикалық активация функциясы. Бұл функция а = logsig(n) = 1/(1 + ехр(-n) ) байланысын сипаттайды. 1. 4 суретінде көрсетілген. Ол сигмоидальді функция тобына кіреді. Және оның аргументі -∞ тен +∞ ке дейінгі диапазон аралығындағы кез келген мәнді қабылдай алады. Ал шығыс 0 мен 1 аралығында ғана өзгереді. ППП Neural Network Toolbox logsig M-функция түрінде берілген. Дифференциалдау қасиетіне байланысты бұл функция жүйелерінде қателіктерді кері тарату негізінде оқытуга қолданылады.
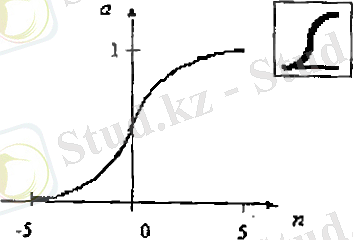 сурет 1. 4
сурет 1. 4
Квадрат ішіндегі сурет функция активациясын көрсетеді. Бұл сурет нейрондық жүйелердің құрылымдық схемаларында қолданылады.
ППП Neural Network Toolbox активациясының басқа да функцияларын қамтиды. Matlab тілін қолдана отырып, пайдаланушы өзінің жеке қайталанбас функцияларын жасай алады.
- Кіріс векторлы нейрон
1. 5 суретте p 1 , p 2 …. . p n R элементтер мен бір векторлы P шығыс векторы көрсетілген. Мұндағы әрбір элементті сәйкесінше w 11 , w 12 …. . w 1R -ге көбейтіледі, және өлшенген мәндер сумматорға жіберіледі. Олардың қосындысы W жолының P кіріс векторына скалярлы көбейтіндісіне тең болады.
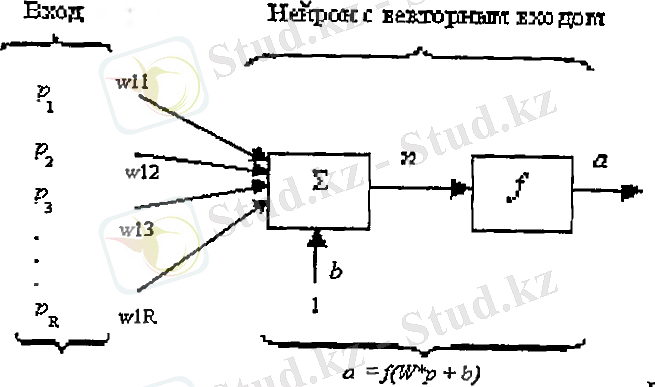 сурет 1. 5
сурет 1. 5
Нейронның кірістердің қосындысымен өлшенетін b жылжуы бар. Нәтижесіндегі n қосынды:
(1. 3)
F активация функциясының аргументі болып табылады. Matlab тілінде мынадай түрде жазылады:
(1. 4)
Үстінде көрсетілген нейронның құрылымында көптеген артық бөлшектер бар.
Көп нейроннан тұратын жүйелерді қарастырғанда нейронның үлкейтілген құрылымдық сұлбасы қолданылады. (сур. 1. 6)
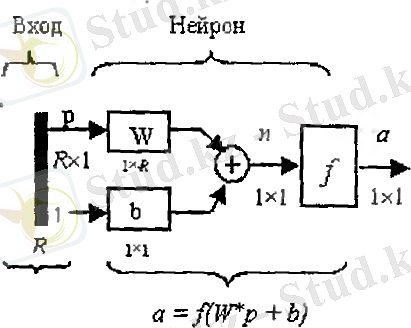 сурет 1. 6
сурет 1. 6
Суретте нейронның кірісі қара вертикальді сызық түрінде көрсетілген. Ол R кіріс элементінің санын көрсетеді. P кіріс векторының өлшемі p символының астында жазылады және Rx1-ге тең. Кіріс векторы ұзындығы R ұзындықты W жол-векторына көбейтіледі. Айта кеткендей, 1 тұрақтысы скалярля жылжу b-ға көбейтілетін кіріс ретінде қарастырылады. Нейронның активация функциясының n кірісі b жылжуы мен WxP көбейтіндісі мен қосындысы болып табылады. Бұл қосынды f активация функциясына айналады және шығыс кезінде нейронның а шығысын аламыз. Мұндағы а-скалярлы шама болып табылады. 1. 6 суретінде көрсетілген құрылымдық сұлба жүйе қабаты деп аталады. Қабат W салмақ, b жылжу WxP көбейту операциясымен f активация функциясмен қосындысы арқылы сипатталады. Р кіріс векторы әдетте қабат сипаттамасына кіреді.
Үлкейтілген құрылымдық сұлбада активация функциясының түрін көрсету үшін арнацы графикалық символдар қолданылады. Олардың кейбір түрлері 1. 7 суретінде көрсетілген. а- баспалдақты, б- сызықты, в- логистикалық.
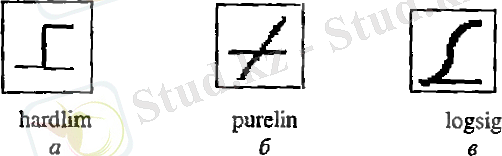 сурет 1. 7
сурет 1. 7
2. Нейрондық жүйелердің архитектурасы
Нейрондық жүйелер бір немесе бірнеше қабаттан тұруы мүмкін. Және оларды сәйкесінше бір қабатты және көп қабатты деп ажыратамыз.
2. 1. Бір қабатты жүйе
R кіріс элементтері мен S-нейрондардан тұратын бір қабатты жүйенің схемасы көрсетілген. (2. 8 сурет)
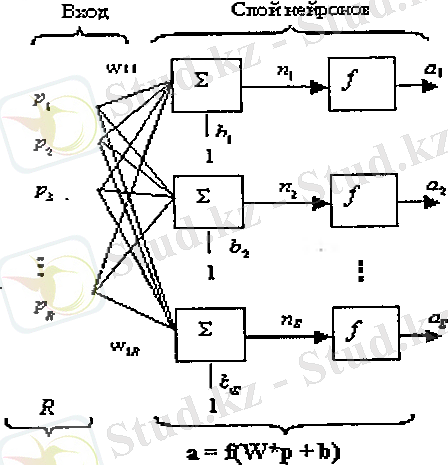 сурет 2. 8
сурет 2. 8
Бұл жүйедегі әрбір вектордың элементі нейронның барлық шығысымен байланысты, және бұл байланыс W массасының матрицасы арқылы беріледі. Сонымен қатар әрбір і -ші нейрон скалярлы шығыс n(i) -ді қалыптастыратын элементтердің жиынтығы болып табылады. n(i) скалярлы функциясының жиынтығы қабаттың п функция активациясының S-элементтік шығыс векторына қосылады. Нейронның қабат шығысы а баған-векторын қалыптастырады, осыдан, нейрон қабатының сипаттамасы мынадай болады:
a = f(W*p+b) . (2. 5)
Қабаттағы R шығыстың саны Sнейронның санымен сәйкес келмеуі мүмкін. Алайда нейрондардың құрылымдық қабаттарын басқа активация функциясын қолданып (2. 8 суреттегідей) жасауға болады. Екі жүйенің де кірістері өзгермейді. Кіріс вектор элементтері жүйеге W масса матрицасы арқылы жіберіледі:
 (2. 6)
(2. 6)
W матрицасының жол индексі нейрон салмағының бағытталуын кқрсетеді, ал баған индекстері - бұл салмақтың кірісінің көзі болып табылады. Осыдан, салмақ матрицасының элементі = W(l, 2) бірінші нейрон жіберу кезінде кірістің екінші элементін көбейтетін коэффицент. S нейрондардан тұратын бірқабатты жүйе үшін үлкейтілген құрылымдық сұлба 2. 9 суретте көрсетілген:
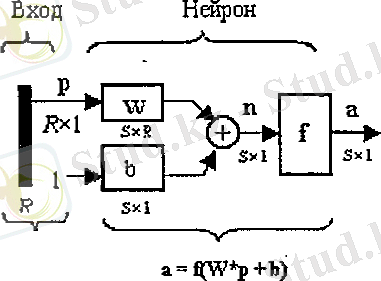 2. 9 сурет
2. 9 сурет
Мұндағы р- Rx1 кіріс векторының өлшемі, w - SxR салмақ матрицасының өлшемі, a, b, n- Sx1өлшемді вектор.
2. 2. Көпқабатты жүйелер
Бірнеше қабатты желіні қарастырайық. Қабаттың кіріс салмағының кірісіне байланысын салмақ матриасы деп, ал қабаттан бөліетін сигналға арналған салмақ матрицасын шығыс қабаттың салмағы деп атаймыз. Енді, нейрондық жүйелерде әр түрлі салмақ пен элементтерге арналған адресаттарды көрсету үшін жоғарғы жағына индекстерді қоямыз. Біріншіден, біз көпқабатты жүйенің бір қабатын қарастырып кетейік:
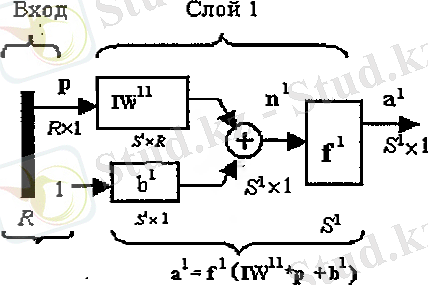 сурет 2. 10
сурет 2. 10
Кірістермен байланысқан салмақ матрицасын IW 11 деп белгілейік, жоғарысындағы индекстер кіріс көзі бірінші қабат екенін, және де бірінші индекс адресатын көрсетеді.
Алдағы уақытта матрицалар үшін кіріс және шығыс қабаттың матрицалары IW (Input Weight) және LW (Layer Weight) деп белгіленеді.
Егер жүйе бірнеше қабаттан тұратын болса, онда әрбір қабат өзінің салмақ матрицасы W , жылжу векторы b және шығыс векторы a болады. Келесі суреттен үш қабаттан тұратын жүйенің структуралық схемасы мен теңдеуі көрсетілген:
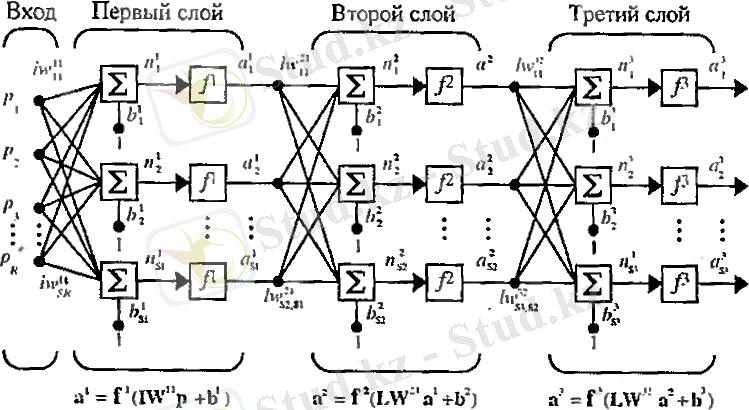 сурет 2. 11
сурет 2. 11
Жоғарыда көрсетілген жүйеде R кіріс, бірінші қабатта S 1 нейрон, екінші қабаттан S 2 тұрады. Әрбір қабат әр түрлі нейродардан тұруы мүмкін. Әр бір нейронға жлжу үшін тұрақты кіріс сигнал 1 берілген. Алдыңғы қабаттың шығысы келесі қабаттың кірісі болады. Содан, 2-ші қабат жүйенің бір қабаты ретінде қарастырылса, S 1 кіріс, S 2 нейрон және S 1 х S 2 салмақ матрицасы W 2 болады.
Көпқабатты жүйелердің қабаты әр түрлі атқ ие болуы мүмкін. Жүйенің шығысын қалыптастыратын қабат шығыс қабат деп аталады. Ал қалған қабаттар жасырынды қабат деп аталады. Жоғарыда көрсетілген үшқабатты жүйе шығыс қабат(3 қабат) және ә жасырын қабат ( 1 және 2 қабат) . Дәл осы жүйенің кеңейтілген структуралық схемасы:
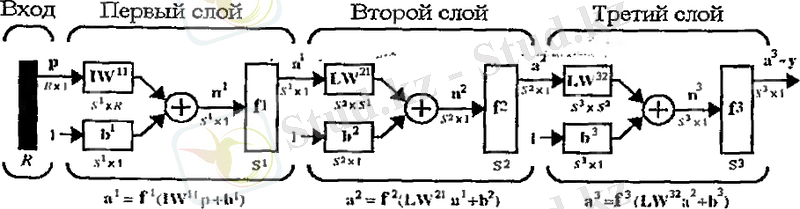
2. 12 сурет
Үшінші қабаттың шығысы а 3 у арқылы белгіленетінін байқаймыз. Бұл шығыс қабат жүйенің соңғы шығысы екенін көрсетеді.
Көп қабатты жүйелердің мүмкіндіктері зор. Мысалы, бірінші қабаты сигмоидальды, ал екінші қабат- сызықты активация функциясынан құралған екі қабатты жүйе кез келген функцияның апроксимация дәлдігін онай анықтап бере алады.
Қорытындылай келе, нейрон функциясының активация кірісі өлшенген кірістің салмағы мен жылжуын анықтайды. Нейронның шығысы нейронның кірісіне және активация функциясының тұріне байланысты. Жалғыз бір нейрон қиын тапсырмаларды орындай алмайды, бірақ бірнешеуін біріктірсе көп мүмкіндіктерге ие бола алады.
Жылжуы бар жүйелер кірісі мен шығыстың арасында күрделі байланыстарды қалыптастыра алады. Мысалы, жылжуы жоқ нейрон кірісіне нөльді берсе, онда активация функциясының кірісі нөльге тең болады.
Көп жағдайда жүйелерде сызықты емемс сигмоидальды активация функциясы логикалық (2. 7 сур. ) немесе гиперболикалық тангенс (2. 13 сур. ) түрінде беріледі.
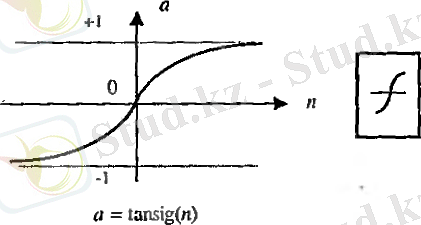 2. 13 сурет
2. 13 сурет
Егер көпқабатты жүйенің соңғы қабаты осындай активация функциясын пайдаланса, жүйенің шығысы шектеулі болады. Қабаттың шығысында сызықты нейрон қолданылса, онда жүйенің шығысы кез келген мәнді қабылдайды. ППП NNT-да осындай активация функциясы бар. Оны алу үшін:
<имя_функции_активации>('deriv ' )
Например, обращение вида
tansig(‘deriv’)
ans = dtansig
гиперболикалық тангенсті есептейтін М-функция, dtansig.
2. 3. Сигналды тікелей жіберу жүйесі
Logsig активация функциясы бір қабатты S нейронды жүйе (R кірісі бар) 2. 14 суретте көрсетілген:
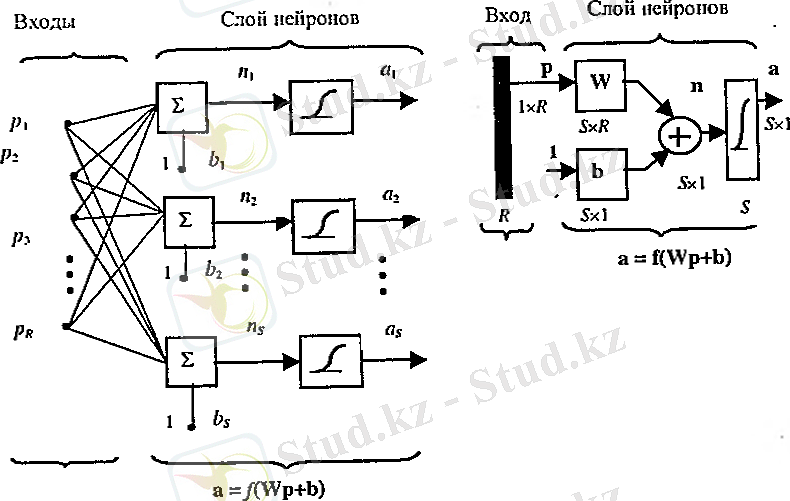
2. 14 сурет
Бұл кері байланысы жоқ жүйе сигналды тікелей жіберу жүйесі деп аталады. Бұндай жүйелер көбіне бір немесе бірнеше жасырын нейрон қабаттары бар сигмоидальды активация функциясы болады.
Жақсырақ түсіну үшін, екіқабатты желіні қарастырайық:
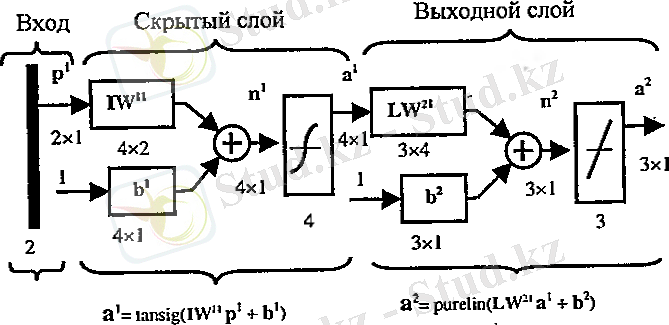 2. 15 сурет
2. 15 сурет
Бұл жүйе функияның аппроксимациясы үшін қолданыла алады.
3. Желілерді инициализациялау, модельдеу және құру
Желі архитектурасын қалыптастыру нейрондық жүйелердің жұмысында бірінші - жүйенің моделін құру. Сигналды тікелей жіберу жүйесін құру. Сигналды тікелей жіберу жүйесін құру үшін ППП NNT- да newff функциясын пайдаланамыз. Ол 4 кіріс және 1 шығыс аргументі- network объектісі.
Бірінші кіріс аргумент - әр кіріс вектор элементтің min немесе max мәндерінің Rx2 өлшем массиві; екінші - әрбір қабат үшін нейрон саны; үшінші - әр қабат үшін активация функцияының ұяшық массиві; төртінші - оқытылатын функция аты. Мысалы, келесі оператор сигналды тікелей жіберу жүйесін құрады:
net = newff([-1 2; 0 5], [3, 1], {‘tansig’, ‘purelin ’ }, ’traingd’) ;
Бұл жүйе [-1 2] және [0 5] мәндерін қабылдайтын екі элементтен тұратын 1 кіріс векторын пайдаланады; бірінші қабатта 2 қабаттан тұратын 3 нейрон және екінші қабатта 1 нейрон. Tansig-бірінші қабатта, purelin-екінші қабатта, traingd-оқытылуда қолданылатын функция.
Newff М-функциясы жүйенің архитектурасын құрып қана қоймай, сонымен қатар салмағы мен жылжуын инициалдайды. Бірақ кей жағдайларда жүйе инициализациясының арнайы редуралары керек ететін кездер болады.
Персептрон
Осы бөлімнен бастап нейронды жүйелердің нақты жүйелік анализі қарастырылады. Және олардың біріншісі персептрон деп аталатын нейрондық жүйе.
Персептрон моделінде қарастырылатын неурон, баспалдақты активация функциясы hardlim қолданылады.
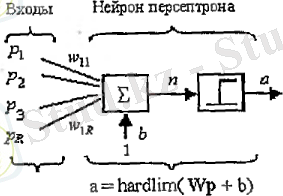
Персептронның әр кіріс вектор элементі сәйкесінше салмағы өлшенген w ij , және олардың көбейтіндісі активация функциясының кірісі болады. Персептронның нейроны 1 ді өлшейді, егер активация функциясы n 0; және 0 болса, n<0;
S нейроны бар жалғыз бір қабаттан тұратын нейрон суретте бейнеленген:
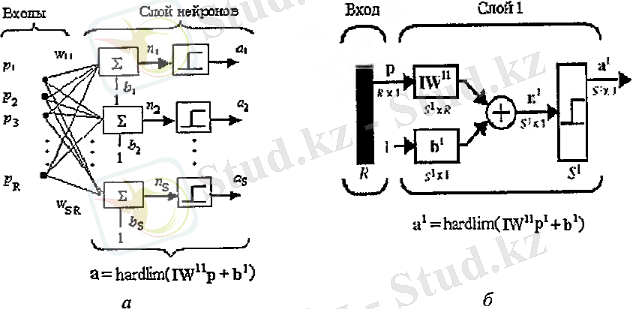
Бір қабатты нейронның теңдеуі:
a = f(Wp+b)
Бір қабатты нейронның моделін қалыптастыру үшін newp функциясы қолданылады.
Net = newp(PR, S)
Функция активация ретінде өздігінен hardlim функциясы қоданылады.
Сызықты жүйелер
Сызықты жүйелер құрылымы бойынша персептрондардіндей, тек активация функциясы ғана сызықты болып келеді. Ондай нейрондық жүйелерді қалыптастыру newlind, newlin функциялары арқылы беріледі.
Суретте екі кірісі бар нейрон бейнеленген purelin активация функциясы қолданылады.
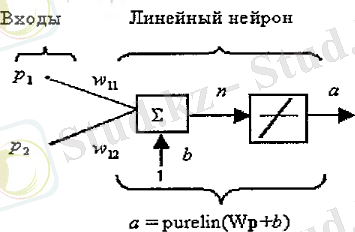
Жүйенің шығысын келесі командамен есептейді:
a = purelin(n) = purelin(Wp+b) = Wp + b = w 11 p 1 + w 12 p 2 +b;
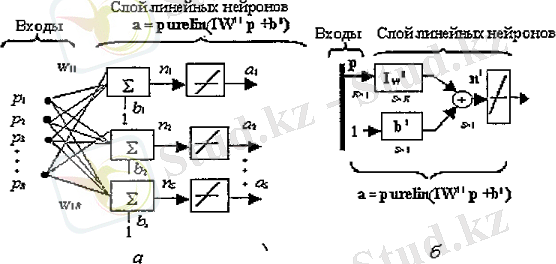
Жоғарыдағы суретте сзықты жүйенің архитектурасы көрсетілген. Ол Matlabта келесі түрде жазылады:
net = newlin([-1 1; -1 1], 1) ;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz