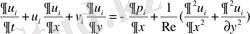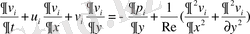Екі араласпайтын және сығылмайтын сұйықтардың канал бойындағы қозғалысы үшін Навье - Стокс теңдеуі және оны жоғары ретті дәлдікпен сандық әдістермен зерттеу жолдары

КІРІСПЕ ...3

1. ЕКІ АРАЛАСПАЙТЫН СҰЙЫҚТЫҢ ҚОЗҒАЛЫСЫ 4
1.1.Екі араласпайтын сұйықтың қозғалыс теңдеуі 4
1.2.Ақырлы айырымдар әдісі 5
1.3.Бастапқы және шекаралық шарттар 5
1.4. F функциясының аппроксимациясы ... ... ... ... ... ... ... ... ... ... ... ..6

2. САНДЫҚ ӘДІСТЕР 7
2.1.Монотонды схема (upwind) ..7
2.2.ENO (Essentially non . oscillatory) схемасы. ... ... ... 8
2.3. Екінші ретті TVD Runge.Kutta әдісі. ... ... ... ... ... ... ... ... ... ... ..9

3.НӘТИЖЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .10

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .12

ПАЙДАЛЫНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..13

ҚОСЫМША А ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 14

Жұмыстың негізі мақсаты екі сығылмайтын және араласпайтын сұйықтың құбыр бойындағы қозғалысы үшін Навье-Стокс теңдеуін жазып, оны жоғарғы ретті дәлдікпен сандық тәсілдермен шешу және алынған нәтижелерді өзара салыстыра отырып ең тиімді әдісті анықтау.
Бұл жұмыста өте қарапайым есеп қарастырылды, яғни екі сұйықтың арасында беттік керілу күші ескерілмеді. Екі сұйықтың құбыр бойындағы қозғалысы үшін Навье-Стокс теңдеуі жазылып, оның бірінші ретті (upwind схемасы) және екінші ретті (ENO схемасы) дәлдікпен сандық әдістермен есептеу жолдары қарастырылды.

1. Роуч П. «Вычислительная гидромеханика» М:Мир,1980. — 618с.
2. Андерсон Д., Таннехилл Дж., Плетчер Р. А65 Вычислительная гидромеханика и теплообмен: В 2-х т. Т. 1: Пер. с англ. —М.: Мир, 1990. —384 с, ил.
3. Mech4480 CFD: Introduction to Flux Corrected Transport M. N. Macrossan, Mechanical Engineering University of Queensland.
4. С. К. Годунов «Разностный метод численного расчета разрывных решений уравнений гидродинамики» М:Мир,1959. —306c.
5. «ESSENTIALLY NON-OSCILLATORY» Division of Applied Mathematics. Brown University. Providence, Rhode Island 02912,U.S.A.

Пән: Автоматтандыру, Техника
Жұмыс түрі: Іс-тәжірибеден есеп беру
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ...3

1. ЕКІ АРАЛАСПАЙТЫН СҰЙЫҚТЫҢ ҚОЗҒАЛЫСЫ4
1.1.Екі араласпайтын сұйықтың қозғалыс теңдеуі4
1.2.Ақырлы айырымдар әдісі5
1.3.Бастапқы және шекаралық шарттар5
1.4. F функциясының аппроксимациясы ... ... ... ... ... ... ... ... ... ... ... ..6

2. САНДЫҚ ӘДІСТЕР 7
2.1.Монотонды схема (upwind)..7
2.2.ENO (Essentially non - oscillatory) схемасы ... ... ... .8
2.3. Екінші ретті TVD Runge-Kutta әдісі. ... ... ... ... ... ... ... ... ... ... ...9

3.НӘТИЖЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 10

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... 12

ПАЙДАЛЫНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ..13

ҚОСЫМША А ... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 14

КІРІСПЕ

Жұмыстың негізі мақсаты екі сығылмайтын және араласпайтын сұйықтың құбыр бойындағы қозғалысы үшін Навье-Стокс теңдеуін жазып, оны жоғарғы ретті дәлдікпен сандық тәсілдермен шешу және алынған нәтижелерді өзара
салыстыра отырып ең тиімді әдісті анықтау.
Бұл жұмыста өте қарапайым есеп қарастырылды, яғни екі сұйықтың арасында беттік керілу күші ескерілмеді. Екі сұйықтың құбыр бойындағы қозғалысы үшін Навье-Стокс теңдеуі жазылып, оның бірінші ретті (upwind схемасы) және екінші ретті (ENO схемасы) дәлдікпен сандық әдістермен есептеу жолдары қарастырылды.

1. ЕКІ АРАЛАСПАЙТЫН СҰЙЫҚТЫҢ ҚОЗҒАЛЫСЫ

Екі араласпайтын сұйық үшін Навье-Стокс теңдеуі [1].

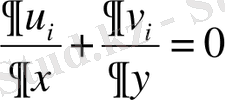- үзіліссіздік теңдеуі.
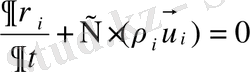- массалардың сақталу заңы.

Біз бұл жағдайда өте қарапайым есепті қарастырамыз. Беттік керілу күшін
ескермейміз.

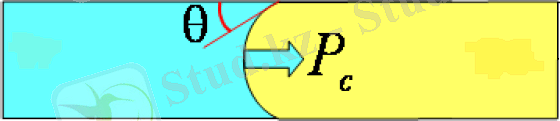
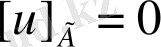
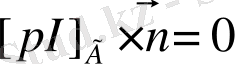
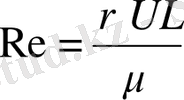
1.1 Екі араласпайтын сұйықтың қозғалыс теңдеуі:

Екі араласпайтын сұйық берілген. Бірінші сұйық қызыл түсті, екіншісі көк түсті. Олар бір-бірімен араласпайды. Осы екі сұйықтын қозғалысын сандық әдістермен зерттеймін.

Екі сұйық болғандықтан тығыздықтары 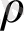бірдей емес. Сондықтан біз тығыздықты айнымалы деп аламыз. Егер F=1 болса, бірінші сұйық; ал егер F=0 болса, екінші сұйық болады.

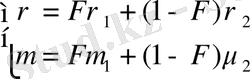F=
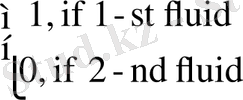
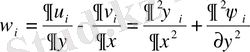- құйын

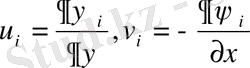
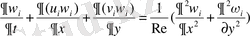
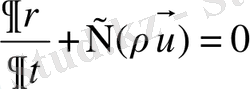
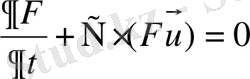
1.2 Ақырлы айырымдар әдісі [2].

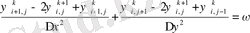
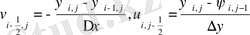
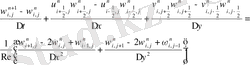
Мұндағы u және v - жылдамдық кампоненттері, ω - құйын, ψ − ағын функциясы.

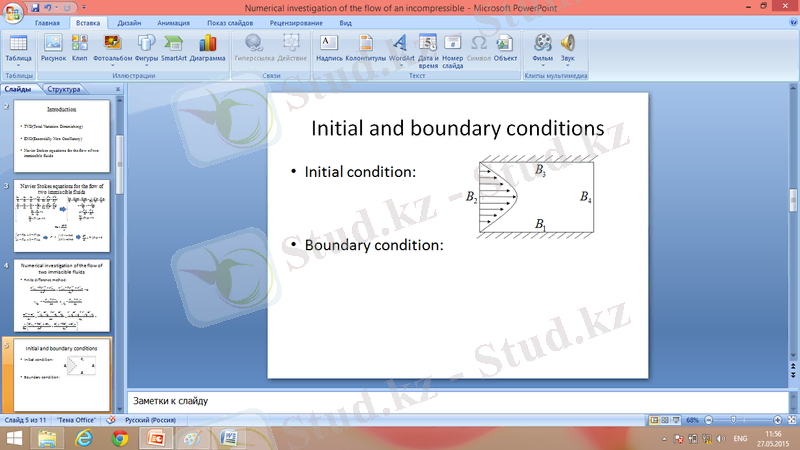
1.3 Бастапқы және шекаралық шарттар.

функциясына қойылған бастапқы шарт: екі сұйық өзара араласпайды.

Шекаралық шарттар:

Ағынның қозғалыс солдан оңға қарай бағытталған. Бірінші және үшінші шекарада сұйық қабырғаға жабысу шарты орындалады. Жылдамдылығы 0-ге тең. Жылдамджықты 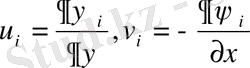интегралдау арқылы ағын функциясын табамыз. Ол тұрақты санға тең болады. Ал интегралдау арқылы 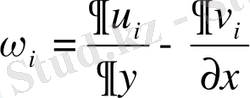құйын функциясын табамыз. Бірінші шекарада ағын функциясының мәнін 0-ге тең деп аламыз. Екінші шекарада ағынды параболалық профиль аламыз. Егер біз түзу сызықты деп алсақ, онда бізде шекаралық шарт дұрыс қойылмаған болады. Себебі біз y=0 және y=H болғанда жылдамдық екі мәнге ие болады.

B1.
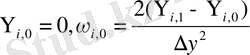
B2.
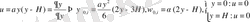
B3.
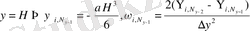
B4.

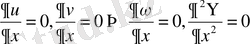
1.4 F функциясының аппроксимациясы.

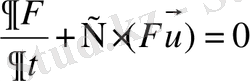
Теңдеудің екінші қосылғышын тор көздерде dy,dx бойынша интегралдаймыз. Ал бірінші қосылғышты уақыт бойынша аппроксимациялаймыз.

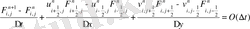
2. САНДЫҚ ӘДІСТЕР.

2.1 Монотонды схема [4].

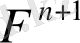
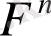
- функциясы монотонды болса, онда - функциясыда монотолды функция болады. Монотонды схеманың бір мысалы: upwind схемасы.

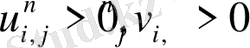
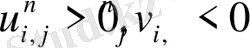
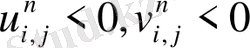
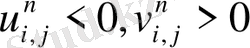
Upwind схемасын қолданғанда бізде сандық диффуция пайда болады:

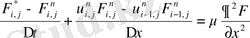
Сандық диффузиядан құтылу үшін біз FCT ( Flux Corrected Transport )-ны пайдаланамыз. FCT ( Flux Corrected Transport )-ның негізгі мақсаты локальді максимум мен локальді минимум жоқ жерлерден сандық диффузияны алып тастау(1-сурет)[3]. Егер локальді максимум мен локальді минимум бар жерден де сандық диффузияны алып тастаса, онда максимум жер онданда көтеріліп, ал минимум бар жер түсіп кетеді. FCT ( Flux Corrected Transport ) локальді максимум мен локальді минимум бар жерде бірінші ретті дәлдікпен, ал локальді максимум мен локальді минимум жоқ жерде екінші ретті дәлдікпен есептейді. Сол себепті бұл схемада бізге дәл шешімді бермейді.

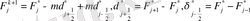
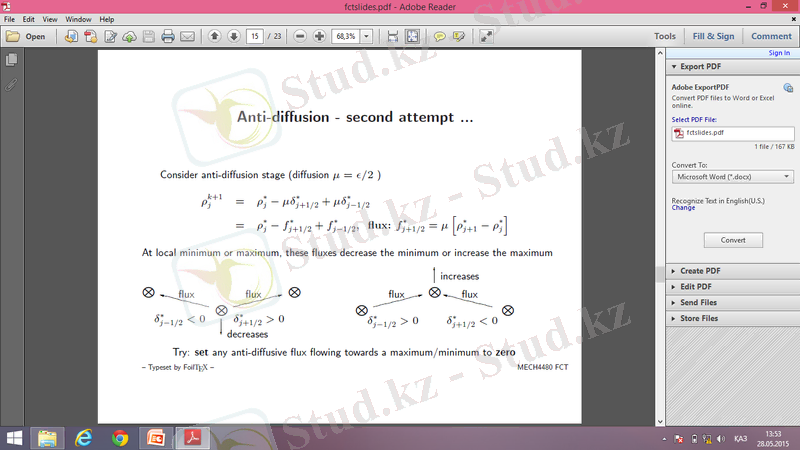
1- Сурет. (Локальді минимум ) (Локальді максиму)

2.2 ENO (Essentially non - oscillatory) схемасы [5].

ENO (Essentially non - oscillatory) схемасы жоғарғы ретті дәлдікпен есептеуге мүмкіндік береді. Екінші ретті дәлдікпен есептеу үшін біз сызықты F=ax+b функциясын қолданамыз.

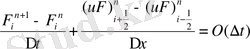
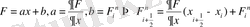
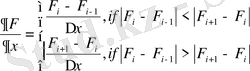
ENO схемасы кеңістік бойынша екінші ретті дәлдікпен, ал уақыт бойынша бірінші ретті дәлдікпен есептейді.ENO(Essentially non-oscillatory) -
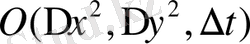. Сол себепті сандық диффузияның әсері аз да болса бар болады. Енді осы диффузиядан құтылу үшін келесі тәсілді қарастырамыз.
2.3 Екінші ретті TVD Runge-Kutta әдісі.
Екінші ретті TVD Runge-Kutta әдісі келесі түрде беріледі:
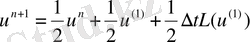1)
2)

Менің қарастырған есебім:
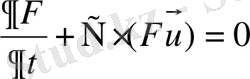
бұл формуланы келесі түрде жазуға болады :

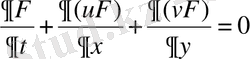
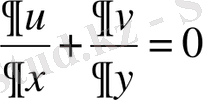
Себебі: - үзіліссіздік теңдеуі. Енді осы берілген формуланы өзіміздің қарастырып отырған есепке қойсақ:

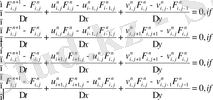
1) Бірінші қадамда біз - ді есептейміз:

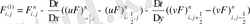
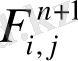
2) Екінші қадамда - ді есептейміз:

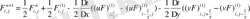
Сонда бізде ENO схемесы уақыт бойынша және кеңістік бойынша да екінші ретті дәлдікпен есептейді.

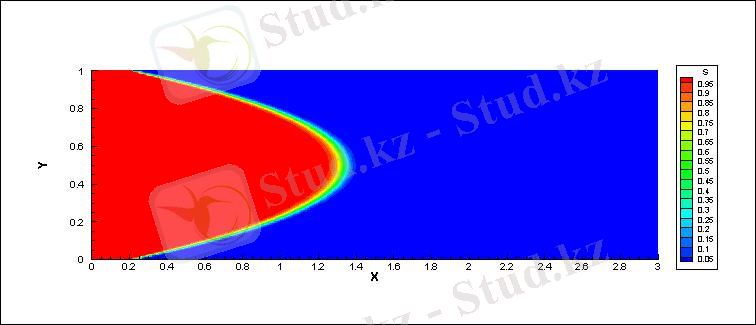
1. НӘТИЖЕ.

- UPWIND 1-st order

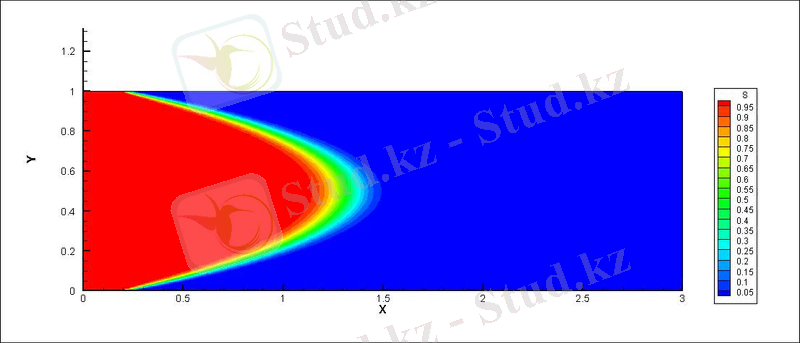
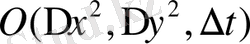
- ENO -

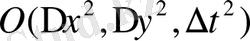
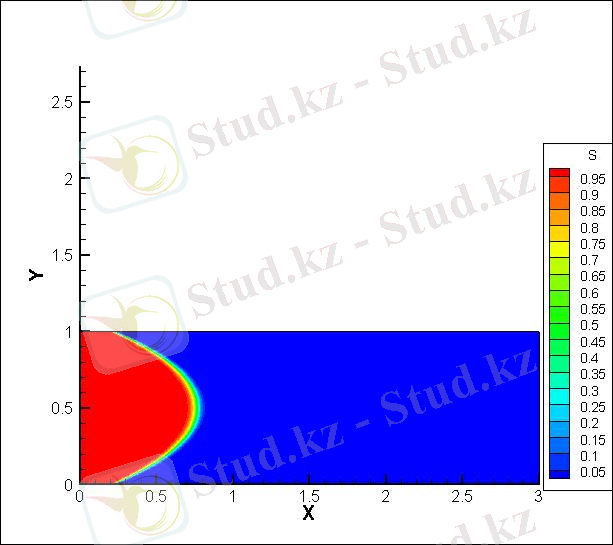
- ENO -

ҚОРЫТЫНДЫ

Мен бұл өндірістік практика барысында екі араласпайтын және сығылмайтын сұйықтардың канал бойындағы қозғалысы үшін Навье - Стокс теңдеуін жазып және оны жоғары ретті дәлдікпен сандық әдістермен зерттеу жолдарын: монотонды схема (upwind), FCT(Flux Corrected Transport) және ENO(Essentially non - oscillatory) схемаларын қарастырдым. Монотонды схема тек бірінші ретті дәлдікпен есептегендіктен онда сандық диффузия пайда болатынын байқадым. ENO(Essentially non - oscillatory) схемасы екінші ретті дәлдікпен есептегендіктен салыстырмалы түрде шешім дәлірек болатынын көрдім.

ПАЙДАЛЫНЫЛҒАН ӘДЕБИЕТТЕР

1. Роуч П. Вычислительная гидромеханика М:Мир,1980. -- 618с.
2. Андерсон Д., Таннехилл Дж., Плетчер Р. А65 Вычислительная гидромеханика и теплообмен: В 2-х т. Т. 1: Пер. с англ. -- М.: Мир, 1990. -- 384 с, ил.
3. Mech4480 CFD: Introduction to Flux Corrected Transport M. N. Macrossan, Mechanical Engineering University of Queensland.
4. С. К. Годунов Разностный метод численного расчета разрывных решений уравнений гидродинамики М:Мир,1959. -- 306c.
5. ESSENTIALLY NON-OSCILLATORY Division of Applied Mathematics. Brown University. Providence, Rhode Island 02912,U.S.A.

ҚОСЫМША А

*
ENO_2-order
*

#define _USE_MATH_DEFINES
#define SQR(A) (A*A)
#include stdio.h
#include stdlib.h
#include direct.h
#include Windows.h
#include math.h

struct flow {

double u;
double v;
};

const double Re = 10.0;

const double alpha = -1.0;

const double CFL = 0.9;
const double CFLD = 0.45;

const double L = 3.0;
const double H = 1.0;

const double Lp = 0.2;

const double U0 = abs(alpha*H*H4);

const double dx = 0.01;
const double dy = 0.01;

const int Nx = Ldx + 1;
const int Ny = Hdy + 1;

const int Npx = Lpdx + 1;

const double dt1 = CFL(U0dx + U0dy);
const double dt2 = CFLD*Re(1dxdx + 1dydy);

const double dt = min(dt1, dt2);

const double epsilon = 0.00000000001;

struct flow** create_massive(int row_count, int col_count) {

struct flow **massive;

massive = (struct flow **)malloc(row_count*sizeof(*massive ));

for(int i = 0; i row_count; i++) {

massive[i] = (struct flow *)malloc(col_count*sizeof(**massive ));
}

return massive;
}

void destroy_massive(struct flow **massive, int row_count, int col_count) {

for(int i = 0; i row_count; i++) {

free(massive[i]);
}

free(massive);
}

double** create_massive_simple(int row_count, int col_count) {

double **massive;

massive = (double **)malloc(row_count*sizeof(*massive ));

for(int i = 0; i row_count; i++) {

massive[i] = (double *)malloc(col_count*sizeof(**massive ));
}

return massive;
}

void destroy_massive_simple(double **massive, int row_count, int col_count) {

for(int i = 0; i row_count; i++) {

free(massive[i]);
}

free(massive);
}

void boundary_condition_psi(double** psi, int nx, int ny, double dx, double dy) {

1 - Bottom boundary condition (no-slip condition) - B1
for(int i = 1; i nx; i++) {

psi[i][0] = 0;
}

2 - Top boundary condition (no-slip condition) - B3
for(int i = 1; i nx; i++) {

psi[i][ny-1] = -alpha*H*H*H6;
}

3 - Left boundary condition (in-flow condition) - B2
for(int j = 0; j ny; j++) {

psi[0][j] = alpha*j*dy*j*dy*(2*j*dy - 3*H)6;
}

4 - Right boundary condition (out-flow condition) - B4
for(int j = 1; j ny-1; j++) {

psi[nx-1][j] = 2*psi[nx-2][j] - psi[nx-3][j];
}
}

void boundary_condition_omega(double **omega, double** psi, int nx, int ny, double dx, double dy) {

1 - Bottom boundary condition (no-slip condition) - B1
for(int i = 1; i nx; i++) {

omega[i][0] = 2*(psi[i][1] - psi[i][0])dydy;
}

2 - Top boundary condition (no-slip condition) - B3
for(int i = 1; i nx; i++) {

omega[i][ny-1] = 2*(psi[i][ny-2] - psi[i][ny-1])dydy;
}

3 - Left boundary condition (in-flow ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.