Логистикалық, Хенон, Лоци және жинақтау-лақтыру типті хаос генераторларының телекоммуникациялық жүйелердегі өткізу қабілетін зерттеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:
КІРІСПЕ
Әр түрлі табиғаттағы (физикалық, бейсызық, радиотехниалық, т. б. ) детерминирленген бейсызық динамикалық жүйелердегі хаосты тербелістердің ашылуы XX ғасыр соңындағы ең үлкен ғылыми жаңалық болды. Бұл құбылысты детерминирленген немесе динамикалық хаос деп атады.
Динамикалық хаос - детерминирленген заңдылықпен анықталатынына қарамастан, бейсызық жүйе тәртібі кездейсоқ болған кездегі динамикалық жүйе теориясындағы құбылыс.
Динамикалық хаостың пайда болу себебі бастапқы шарттар мен параметрлердің тұрақсыздығы (сезімталдығы) болып табылады: бастапқы шарттың уақыт өте өзгеруі жүйе динамикасына аса үлкен өзгеріс алып келеді.
Динамикалық хаостың пайда болуы жаңа маңызды инженерлік идеялар берді, осылардың негізінде қазіргі практикада қолданып жүрген құрылғылар мен теориялардың құрылуына алып келді. Көптеген радиотехникалық, нанотехнологиялық лабороторияларда электронды құрылғыларды пайда болатын жоғары өткізу қабілеті бар, хаосты тербелістерді қолдана отырып ақпаратты жіберу үшін тиімді құрылғылар зерттелуде.
Қазіргі таңда технологияның қарқынды дамуына байланысты ақпаратты өзгеріссіз жіберудің көптеген жаңа әдістері пайда болды. Ал хаос генераторлары тек аз ғана ақпаратты аз ғана қашықтыққа жіберумен шектелді.
Осы жұмыста белгілі хаос генераторлары, логистикалық бейнелеу, Лоци, «жинақтау-лақтыру» генераторлары қарастырылды. Олардың хаос жүйесіндегі тербелістерінің реализациясы мен фазалық портреттері QT программалау тілінде алынды. Тербелістің хаостық жүйедегі орнын анықтайтын басқарушы параметрлерін өзгерте отырып, адамның есту диапазоны 20 кГц-ке дейінгі аралықтағы өткізу қабілеттері анықталды. Алынған нәтижелер кестелерге орналастырылып, MatLab ортасында хаос генераторларының жиілігі мен өткізу қабілеті арасындағы тәуелділік графигі алынды. Осы графиктің көмегімен хаос генераторларының өткізу қабілеттері жоғары екені дәлелденді.
Диплoмдық жұмыcтың мақcаты: бірнеше хаос генераторларының өткізу қабілеттерін зерттеу арқылы телекоммуникациялық жүйедегі маңызын анықтау.
Диплoмдық жұмыcтың өзeктілігі: ақпаратты жіберу жүйесінде динамикалық хаосты пайдалану барысында пайда болатын ауытқулар берілген параметрлермен хаосты тербелістерді алуға, өткізу қабілеті жоғары хаос генераторлары арқылы ақпаратты жіберудің қауіпсіздігіне негізделген.
- БЕЙСЫЗЫҚ ЖӘНЕ ХАОСТЫҚ БЕЙНЕЛЕР
Динамикалық хаос үздіксіз спектрі бар күрделі периодсыз тербелістің бейсызық динамикалық жүйесіндегі пайда болатын кең таралған құбылысты сипаттайды [1] .
Хаосты тербеліс - бұл толығымен детерминирленген жүйеде реттелмеген қозғалыстардың пайда болуы. Хаосты тербелістерді зерттеу өзімен бірге жаңа идеяларды алып келеді, олар көптеген себептермен инженерлік зерттеулерде маңызды рөл атқарады [2] .
Хаосты тербелістердің ерекшелігі - жоғары сезімталдық, бастапқы шартқа аз өзгерту енгізгеннің өзінде сезеді.
Дискретті бейнелеулердің сандық байланыс жүйесінде қолданылуы генерациялау және хаосты процесстерді өңдеуге арналған сандық сигналдық процессорлардың негізінде стандартты және өңделген шешімдерді қолдануға мүмкіндік бергендітен, сонымен қатар ақпарат пен сигналды өңдеудің сандық әдістерін барлық жерге практикалық түрде енгізгендіктен өте ыңғайлы болып келеді.
Хаосты тербелістердің дискретті генераторларының қасиеттері бейнелеу функциясының түрімен және басқарушы параметрлерінің мәндерімен анықталады [3] .
- Логистикалық бейнелеу
Логистикалық бейнелеуді қарастырайық:
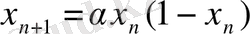 (1. 1)
(1. 1)
мұндағы,
 - басқарушы параметр. Логистикалық бейнелеуді параболалық бейнелеу көрсеткендіктен квадраттық бейнелеу деп те атайды [4] .
- басқарушы параметр. Логистикалық бейнелеуді параболалық бейнелеу көрсеткендіктен квадраттық бейнелеу деп те атайды [4] .
Логистикалық бейнелеудің негізгі қасиеттерін қарастырайық. Cурет 1. 1-де бифуркациялық диаграмма мен Ляпунов көрсеткіші көрсетілген.
Логистикалық бейнелеуде (сурет 1. 1) Ляпунов көрсеткішін пайдаланып, хаосты режимде болатын
параметрінің мәнін таңдауға болады.
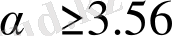 болған кездегі логистикалық бейнелеу үшін Ляпунов көрсеткіші оң болады және жүйеде тербелістің хаосты режимі байқалады. Бейнелеу параметрінің мәні процесстің хаостылық деңгейін анықтайды және жүйеде бола алатын мүмкін болатын күй сандары.
болған кездегі логистикалық бейнелеу үшін Ляпунов көрсеткіші оң болады және жүйеде тербелістің хаосты режимі байқалады. Бейнелеу параметрінің мәні процесстің хаостылық деңгейін анықтайды және жүйеде бола алатын мүмкін болатын күй сандары.
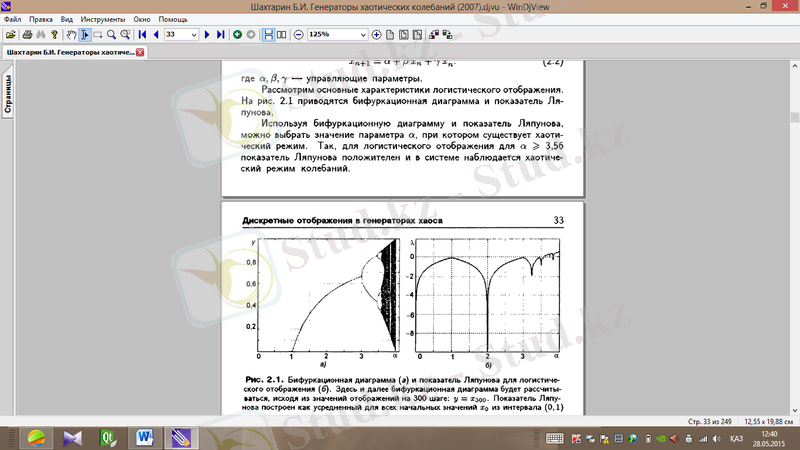
(а) (ә)
Cурет 1. 1. Логистикалық бейнелеу үшін бифуркациялық диаграмма (а) мен Ляпунов көрсеткіші (ә)
Параметрдің өзгеруі сипаттамаға бастапқы шарттың өзгеруінен күштірек әсерін тигізеді. Бейнелеу параметрінің мәні процесстің хаостылығының деңгейін, яғни жүйе сол жерде бола алатын мүмкін болатын қалыптың санын анықтайды. Сигнал тұйықтығы мен шуылдан қорғаудың шыңына жету үшін энтропияның үлкеюіне сәйкес келетін сондай күйлердің көп болуы қажет.
- Жартышеңбер бейнелеуі
Келесі бейнелеу жартышеңбер бейнелеуі деп аталад және мына формуламен есептеледі:
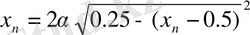 (1. 3)
(1. 3)
мұндағы,
 - басқарушы параметр.
- басқарушы параметр.
Бұл бейнелеу гистограммның мәні максималды болған жағдайда да мүмкін болатын мәндердің барлық аралығын алмайтынымен қызықты болып келеді [5] .
Хаосты тербелістің (сурет 1. 2) режимі басқарушы параметр мәнінің аз диапазонында жүзеге асады. Осы сипаттаманың озінен жартышеңбер бейнелеуі қалған бейнелеулерге қарағанда ақпаратты жіберуге қолайлы болы келеді.
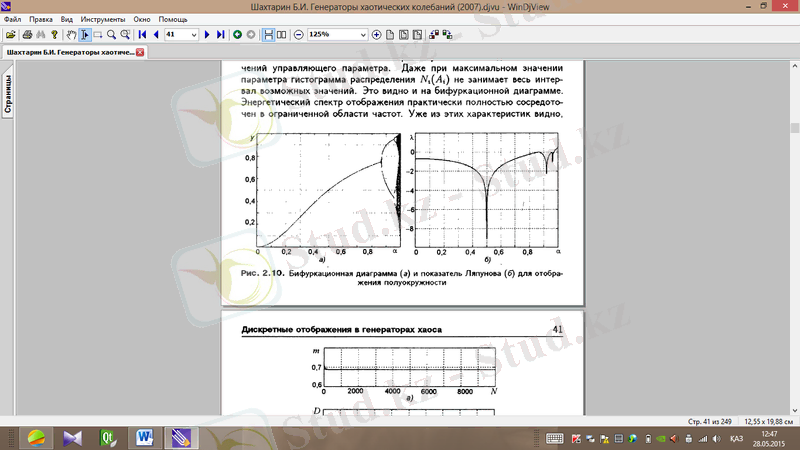
(а) (ә)
Cурет 1. 2. Жартышеңбер бейнелеуі үшін бифуркациялық диаграмма (а) мен Ляпунов көрсеткіші (ә)
Синус функциясы секілді квадраттың түбірін шығару функциясы әр түрлі тілдерде және әр түрлі құрылғы платформаларында тербелмелі процесстердің ажыратылатын реализациясын алуға алып келетін әр түрлі нүктелермен жүзеге асады. Бұл қасиет санкцияланбайтын қолжетімділіктің күрделенуі үшін қолданылуы мүмкін. Бірақ, басқа жағынан, бұл осы бейнелеуді ақпаратты жіберудің конфеденциалды жүйесінде қолдануға шектеу қояды.
Жартышеңбер бейнелеуінің реализациясы мен фазалық портреті (сурет 1. 3, 1. 4) көрсетілген.
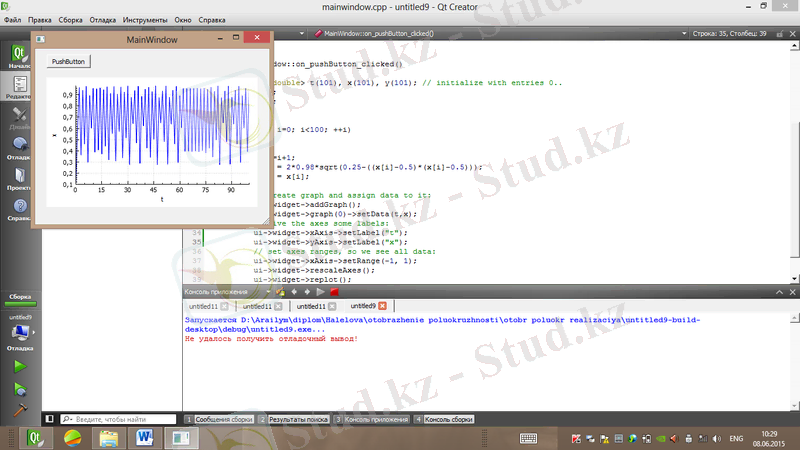
Сурет 1. 3. Жартышеңбер бейнелеуінің реализациясы(α=0. 98)
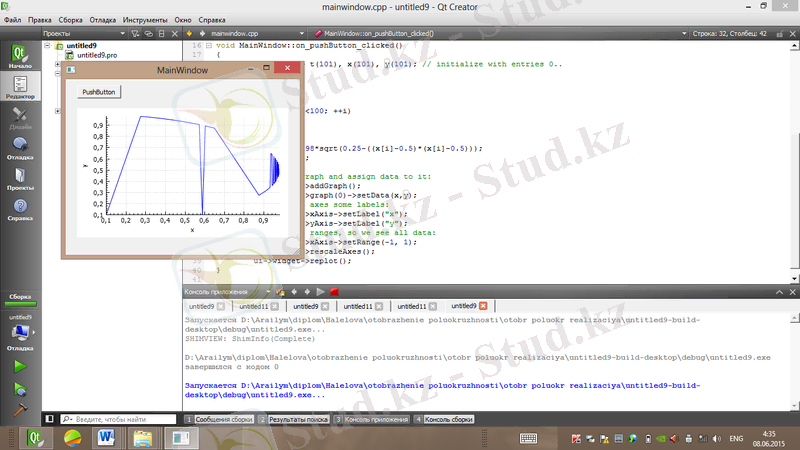
Сурет 1. 4. Жартышеңбер бейнелеуінің фазалық портреті
- Гармоникалық бейнелеу
Тағы бір бірпараметрлі бейнелеу жүйесін гармоникалық бейнелеуден алуға болады:
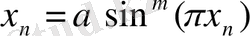 (1. 4)
(1. 4)
мұндағы,
 - басқарушы параметр,
- басқарушы параметр,
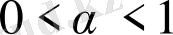 ;
;
 - жалпы жағдайда негізсіз мәнді, сонымен қатар бөлшек мәнді қабылдайтын деңгей көрсеткіші [6] .
- жалпы жағдайда негізсіз мәнді, сонымен қатар бөлшек мәнді қабылдайтын деңгей көрсеткіші [6] .
Деңгей көрсеткішінің бейнелеу қасиетіне ықпалын қарастырайық. Cурет 1. 5-те
 мәні әр түрлі болған жағдайдағы бейнелеу графигі көрсетілген.
мәні әр түрлі болған жағдайдағы бейнелеу графигі көрсетілген.
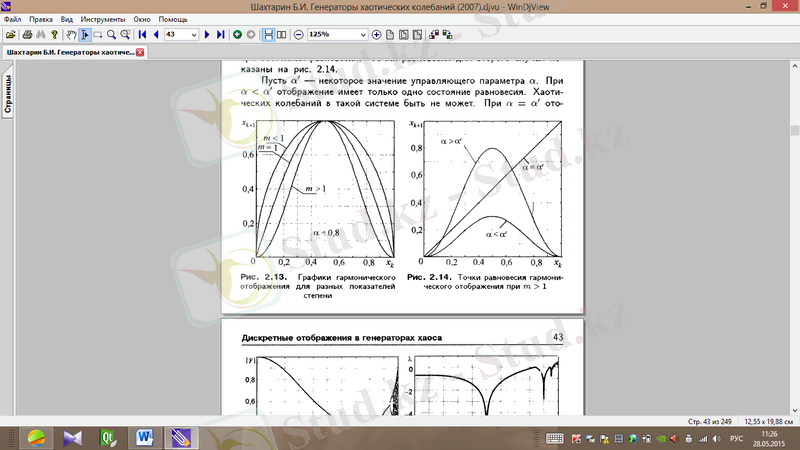
Cурет 1. 5. Әр түрлі деңгей көрсеткіштері үшін гармоникалық бейнелеудің графиктері
Деңгей көрсеткішінің бірден төмен және бірден жоғары болғандағы жағдайын бөлек қарастырайық. Бірінші жағдайда бейнелеуде теңдік екі нүктеден аспайды, екінші жағдайда - теңдіктің бір немесе үш күйі болады.
Деңгей көрсеткіші бірден жоғары болған жағдайдағы теңдік нүктесі сурет 1. 6-да көрсетілген.
Сурет 1. 6-да көрсетілгендей
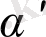 -
-
 басқарушы параметрдің кейбір мәні болсын делік.
басқарушы параметрдің кейбір мәні болсын делік.
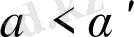 болған кезде бейнелеу тек бір ғана теңдік күйінде болады. мұндай жүйеде хаосты тербелістің болуы мүмкін емес.
болған кезде бейнелеу тек бір ғана теңдік күйінде болады. мұндай жүйеде хаосты тербелістің болуы мүмкін емес.
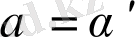 болғанда бейнелеуде теңдіктің екі күйі болады.
болғанда бейнелеуде теңдіктің екі күйі болады.
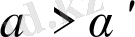 бейнелеуде теңдіктің үш күйі болады. Егер бастапқы шарт теңдіктің екінші нүктесінің аргументінің мәнін арттырмаса, онда процесс тез өшеді. Егер бастапқы шарт теңдіктің екінші нүктесінің аргументінің мәнін арттырса, онда жүйе шығысында саны теңдіктің үшінші нүктесінің аргументінен көп мөлшерде қалыс қалмайтын хаос пайда болады. Ереже бойынша, мұндай хаосты тербеліс біртіндеп өшеді.
бейнелеуде теңдіктің үш күйі болады. Егер бастапқы шарт теңдіктің екінші нүктесінің аргументінің мәнін арттырмаса, онда процесс тез өшеді. Егер бастапқы шарт теңдіктің екінші нүктесінің аргументінің мәнін арттырса, онда жүйе шығысында саны теңдіктің үшінші нүктесінің аргументінен көп мөлшерде қалыс қалмайтын хаос пайда болады. Ереже бойынша, мұндай хаосты тербеліс біртіндеп өшеді.

Cурет 1. 6.
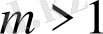 болған кездегі гармоникалық бейнелеудің теңдік нүктесі
болған кездегі гармоникалық бейнелеудің теңдік нүктесі
 және
және
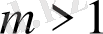 болған жағдайдағы бифуркациялық диаграмма және Ляпунов көрсеткіші cурет 1. 7, 1. 8-де көрсетілген.
болған жағдайдағы бифуркациялық диаграмма және Ляпунов көрсеткіші cурет 1. 7, 1. 8-де көрсетілген.
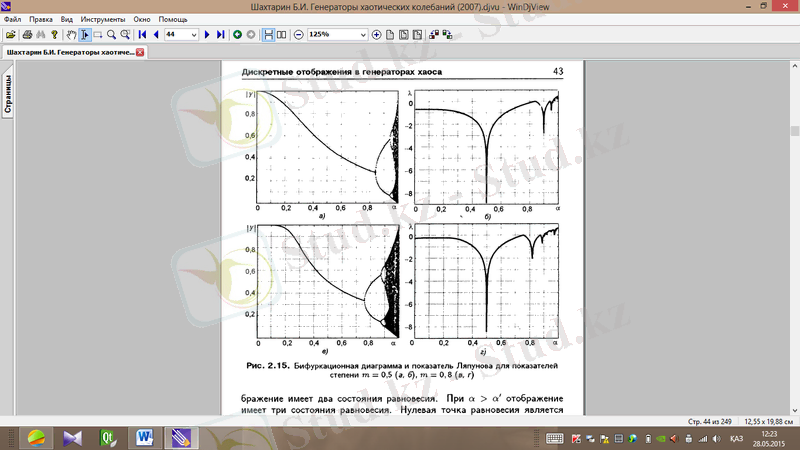
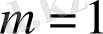 болған кезде бейнелеудің хаос облысы тар болады. m мәні үлкейген сайын хаос облысы да кеңейеді. Осы кезде Шарковский терезелерінің саны көп болады.
болған кезде бейнелеудің хаос облысы тар болады. m мәні үлкейген сайын хаос облысы да кеңейеді. Осы кезде Шарковский терезелерінің саны көп болады.
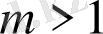 болған кезде, хаосты режим облысы тарылады, хаос облысы параметр азайған жаққа ығысады, хаостың динамикалық диапазоны азаяды, Шарковский терезелері жойылады.
болған кезде, хаосты режим облысы тарылады, хаос облысы параметр азайған жаққа ығысады, хаостың динамикалық диапазоны азаяды, Шарковский терезелері жойылады.
Осылайша,
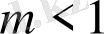 болған кез (сурет 1. 7) алдыңғы қарастырған бейнелеулерге ұқсас келеді.
болған кез (сурет 1. 7) алдыңғы қарастырған бейнелеулерге ұқсас келеді.
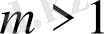 мәні (сурет 1. 8) хаосты тербелістердің диапазоны үлкен емес және Шарковский терезелері бар болғандықтан, ақпаратты жіберуге қолайлы емес.
мәні (сурет 1. 8) хаосты тербелістердің диапазоны үлкен емес және Шарковский терезелері бар болғандықтан, ақпаратты жіберуге қолайлы емес.
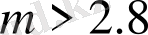 мәнінде хаосты режим бақыланғанымен, олар хаосты жарқырауға сәйкес келеді.
мәнінде хаосты режим бақыланғанымен, олар хаосты жарқырауға сәйкес келеді.
(а) (ә)

(б) (в)
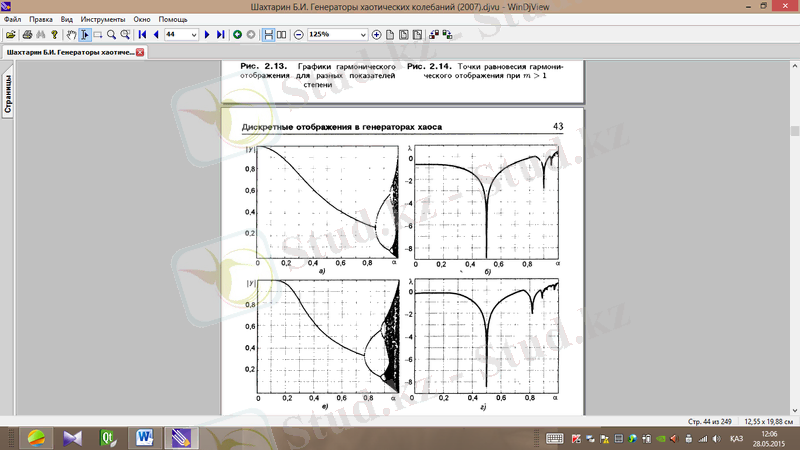
Cурет 1. 7.
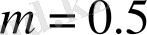 (а, ә),
(а, ә),
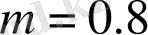 (б, в) болған кездегі деңгей көрсеткіші үшін бифуркациялық диаграмма мен Ляпунов көрсеткіші
(б, в) болған кездегі деңгей көрсеткіші үшін бифуркациялық диаграмма мен Ляпунов көрсеткіші
(а) (ә)
(б) (в)
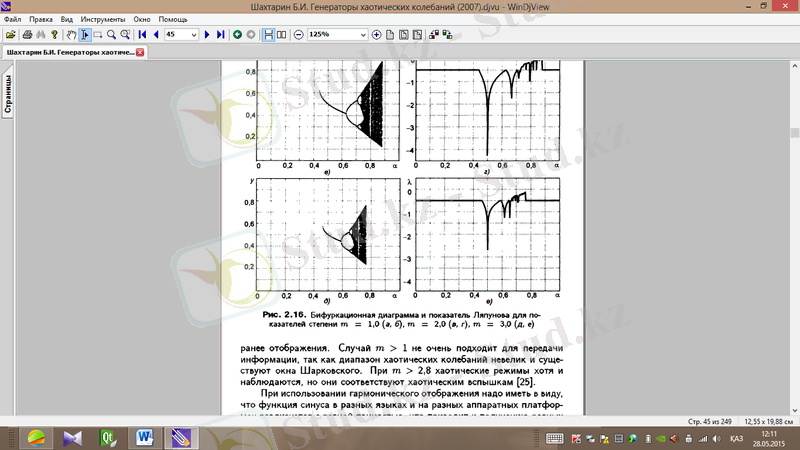
Cурет 1. 8.
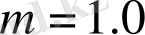 (а, ә),
(а, ә),
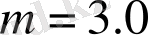 (б, в), болған кездегі деңгей көрсеткіші үшін бифуркациялық диаграмма мен Ляпунов көрсеткіші
(б, в), болған кездегі деңгей көрсеткіші үшін бифуркациялық диаграмма мен Ляпунов көрсеткіші
Гармоникалық бейнелеудің реализациясы мен фазалық портреті сурет 1. 9, 1. 10-да көрсетілген.
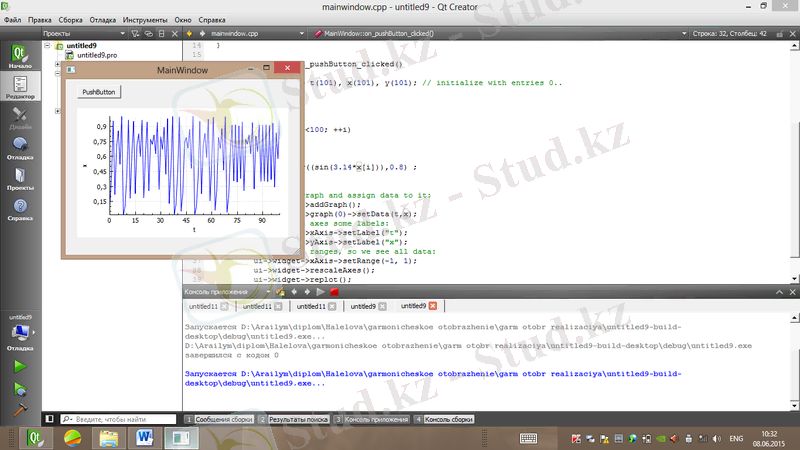
Сурет 1. 9. Гармоникалық бейнелеу реализациясы (α=1)
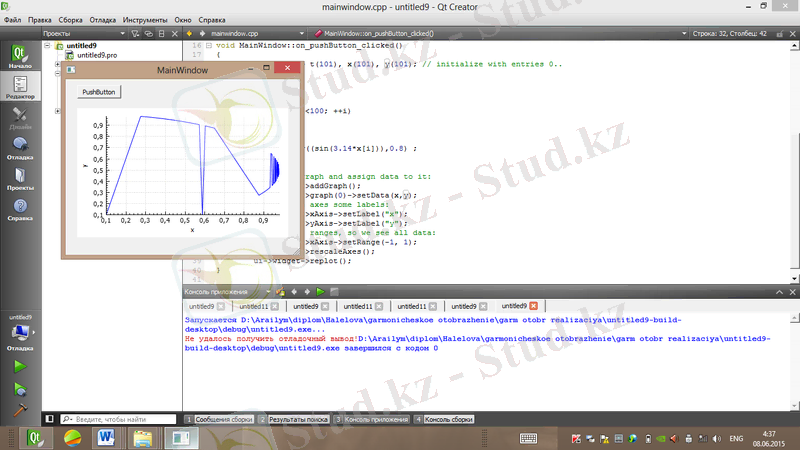
Сурет 1. 10. Гармоникалық бейнелеудің фазалық портреті
- Дәрежелік бейнелеу
Дәрежелік бейнелеуді қарастырайық.
, (1. 5)
 - басқарушы параметр,
- басқарушы параметр,
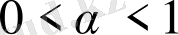 ,
,
 - деңгей көрсеткіші.
- деңгей көрсеткіші.
Деңгей көрсеткішінің бейнелеу қасиетіне ықпалын қарастырайық. Cурет 1. 11-де әр түрлі
 мәніндегі бейнелеу графиктері көрсетілген.
мәніндегі бейнелеу графиктері көрсетілген.
Гармоникалық бейнелеу секілді дәрежелік бейнелеу де (сурет 1. 11) дәрежелік типті бейнелеу үшін
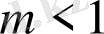 мәнін қарастырмағанда,
мәнін қарастырмағанда,
 параметрінің барлық мәні және
параметрінің барлық мәні және
 параметрі мәнінің барлық облыстары үшін тегіс экстремумды көрсетеді.
параметрі мәнінің барлық облыстары үшін тегіс экстремумды көрсетеді.
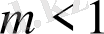 мәні үшін бейнелеу функциясының бірінші туындысында ажырайтын «өткір» экстремумды көрсетеді. Ляпунов көрсеткішін анықтау барысында, ереже бойынша, жарылыс нүктесін анықтағанға дейінгі жолда жояды.
мәні үшін бейнелеу функциясының бірінші туындысында ажырайтын «өткір» экстремумды көрсетеді. Ляпунов көрсеткішін анықтау барысында, ереже бойынша, жарылыс нүктесін анықтағанға дейінгі жолда жояды.
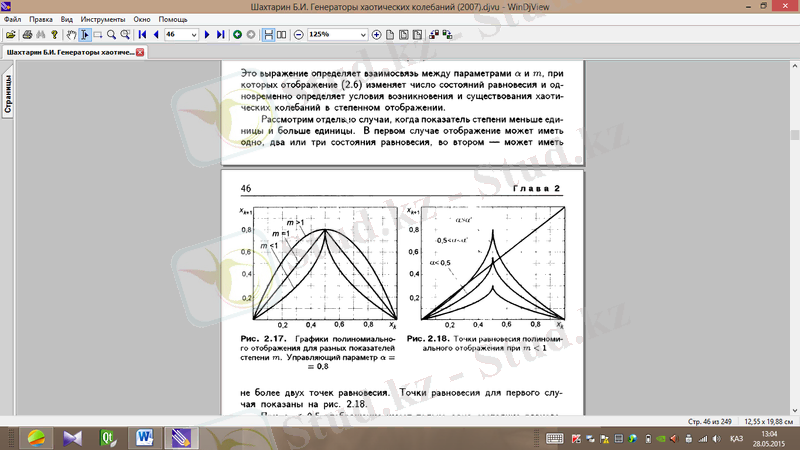
Cурет 1. 11. Әр түрлі
 деңгей көрсеткіші үшін дәрежелік бейнелеу графиктері. Басқару параметрі
деңгей көрсеткіші үшін дәрежелік бейнелеу графиктері. Басқару параметрі
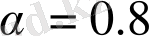
Деңгей көрсеткіші бірден кіші және бірден үлкен болған жағдайларын бөлек қарастырайық. Бірінші жағдайда бейнелеуде теңдіктің бір, екі немесе үш күй болуы мүмкін, екіншісінде - теңдік екі нүктеден аспайды. Бірінші жағдай үшін теңдік нүктесі сурет 1. 12-де көрсетілген.
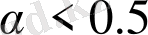 болған кезде бейнелеуде теңдіктің бір ғана күйі болады. Мұндай жүйеде хаосты тербелістің болуы мүмкін емес.
болған кезде бейнелеуде теңдіктің бір ғана күйі болады. Мұндай жүйеде хаосты тербелістің болуы мүмкін емес.
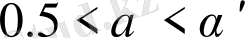 болған кезде, мұндағы
болған кезде, мұндағы
 - параметрдің кейбір мәні, бейнелеуде үш күй болады. теңдіктің нөлдік нүктесі тұрақты, ал қалған екі нүктесі тұрақсыз болады. егер бастапқы шарт теңдіктің екінші нүктесін арттырса, онда
- параметрдің кейбір мәні, бейнелеуде үш күй болады. теңдіктің нөлдік нүктесі тұрақты, ал қалған екі нүктесі тұрақсыз болады. егер бастапқы шарт теңдіктің екінші нүктесін арттырса, онда
Cурет 1. 12.
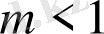 болған кездегі дәрежелік бейнелеудің теңдік нүктесі.
болған кездегі дәрежелік бейнелеудің теңдік нүктесі.
жүйенің шығысында хаостық тербелістер көріне бастайды. Ереже бойынша, мұндай хаосты режим уақыт өте келе сөнеді және жүйе нөлге орнайды
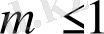 және
және
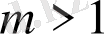 жағдайлары үшін бифуркациялық диаграммалары сурет 1. 13, 1. 14-те көрсетілген.
жағдайлары үшін бифуркациялық диаграммалары сурет 1. 13, 1. 14-те көрсетілген.
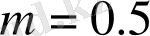 мәнінде бейнелеуде хосты тербелістің облысы тар болады.
мәнінде бейнелеуде хосты тербелістің облысы тар болады.
 артқан сайын хаос облысы кеңейеді (сурет 1. 13, (ә) ), Бұл жерде Шарковский терезелері болмайды.
артқан сайын хаос облысы кеңейеді (сурет 1. 13, (ә) ), Бұл жерде Шарковский терезелері болмайды.
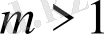 болғанда (сурет 1. 14) хаосты режим облысы тарылады, Шарковский терезелері пайда болады.
болғанда (сурет 1. 14) хаосты режим облысы тарылады, Шарковский терезелері пайда болады.
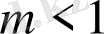 жағдайы Шарковский терезесі болмағандықтан, ақпаратты жіберу жүйесінде берілген бейнелеуді қолдануға мүмкіндік береді.
жағдайы Шарковский терезесі болмағандықтан, ақпаратты жіберу жүйесінде берілген бейнелеуді қолдануға мүмкіндік береді.

(а) (ә)
Cурет 1. 13.
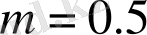 (а),
(а),
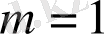 (ә) деңгей көрсеткіштері үшін бифуркациялық диаграммалар
(ә) деңгей көрсеткіштері үшін бифуркациялық диаграммалар
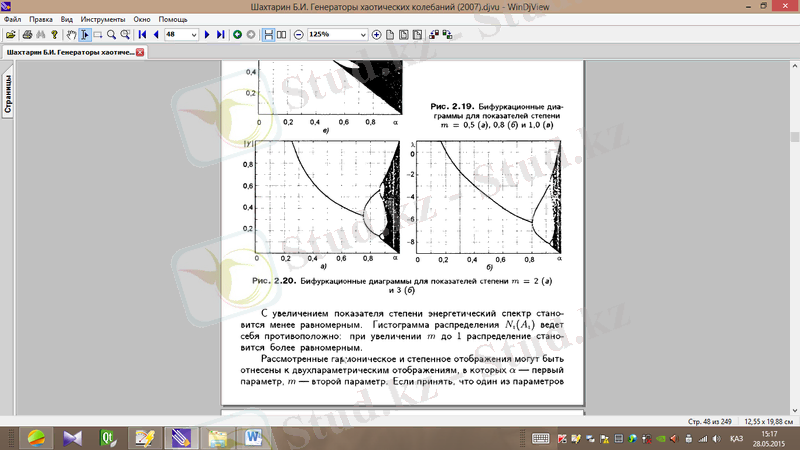
Cурет 1. 14.
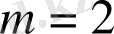 деңгей көрсеткіші үшін бифуркациялық диаграмма
деңгей көрсеткіші үшін бифуркациялық диаграмма
Дәрежелік бейнелеу генераторының реализациясы мен фазалық портреті сурет 1. 15, 1. 16-да көрсетілген.
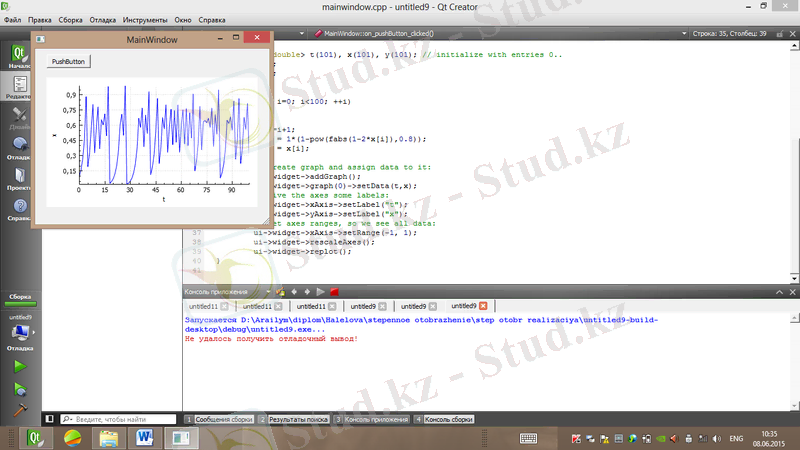
Сурет 1. 15. Дәрежелік бейнелеу реализациясы (α=1, m=0. 8)
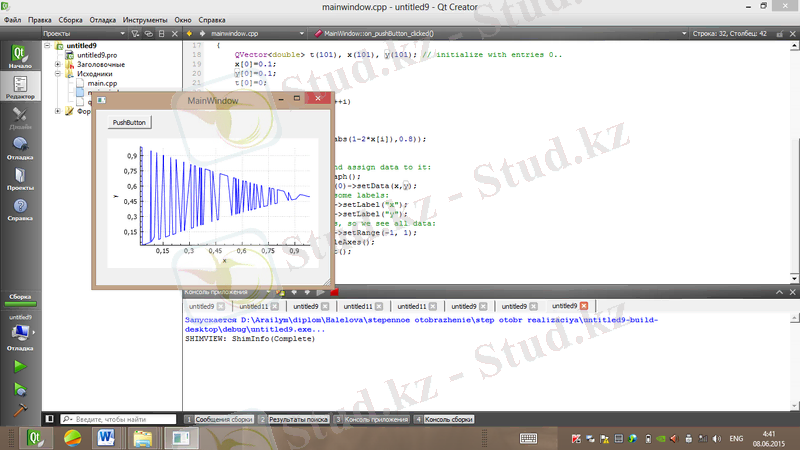
Сурет 1. 16. Дәрежелік бейнелеудің фазалық портреті
- Ығысу бейнелеуі
Ығысу бейнелеуі мынадай түрде болады:
. (1. 6)
Бұл бейнелеуді Бернулли ығысуы деп те атайды.
 параметрінің мәніне тәуелділігіне байланысты
параметрінің мәніне тәуелділігіне байланысты
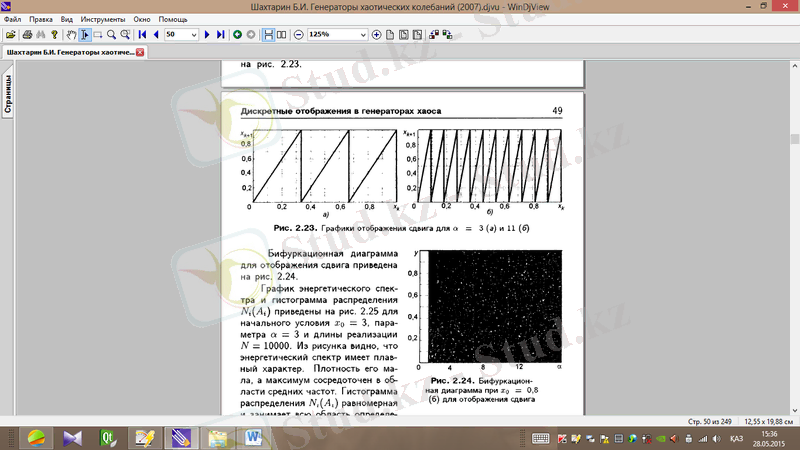
 -типті Бернулли ығысуын ажыратады. Үштік және он бірлік Бернулли ығысуының графиктері сурет 1. 17-де көрсетілген.
-типті Бернулли ығысуын ажыратады. Үштік және он бірлік Бернулли ығысуының графиктері сурет 1. 17-де көрсетілген.
(а) (ә)
Cурет 1. 17.
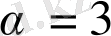 (а) және
(а) және
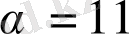 (ә) мәні үшін ығысу бейнелеуінің графигі
(ә) мәні үшін ығысу бейнелеуінің графигі
Ығысу бейнелеуі үшін бифуркациялық диаграмма сурет 1. 18-де көрсетілген.
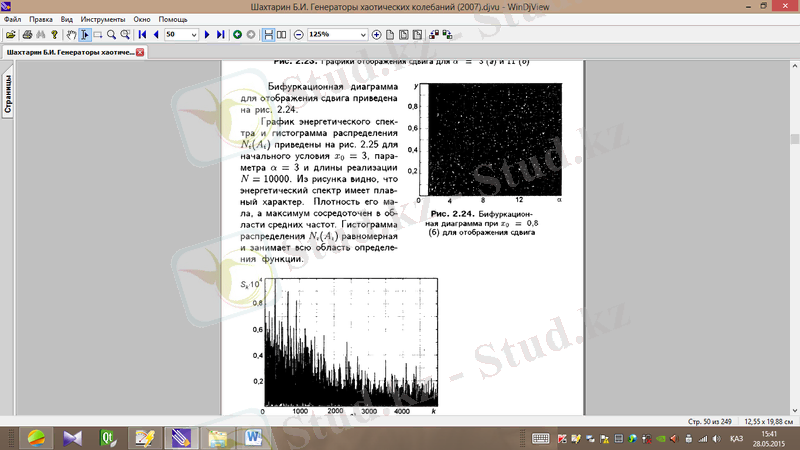
Cурет 1. 18. Ығысу бейнелеуі үшін
 жағдайындағы бифуркациялық диаграмма.
жағдайындағы бифуркациялық диаграмма.
Ығысу бейнелеуінің реализациясы мен фазалық портреті сурет 1. 19, 1. 20-да көрсетілген.
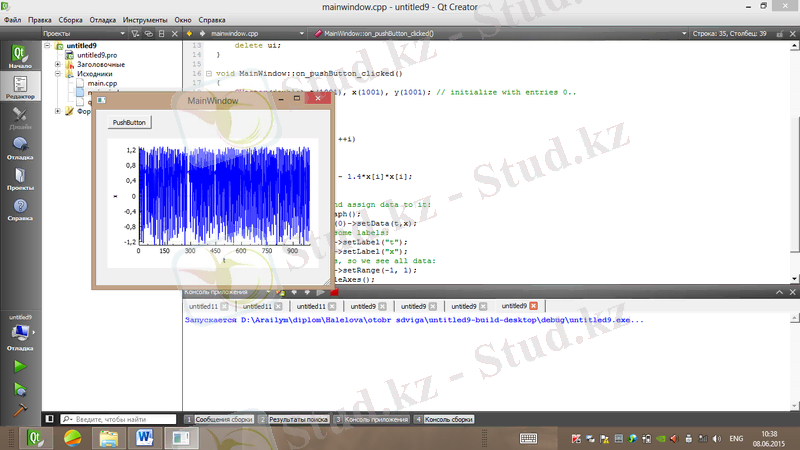
Сурет 1. 19. Ығысу бейнелеуінің реализациясы (a=1. 4, b=0. 3)
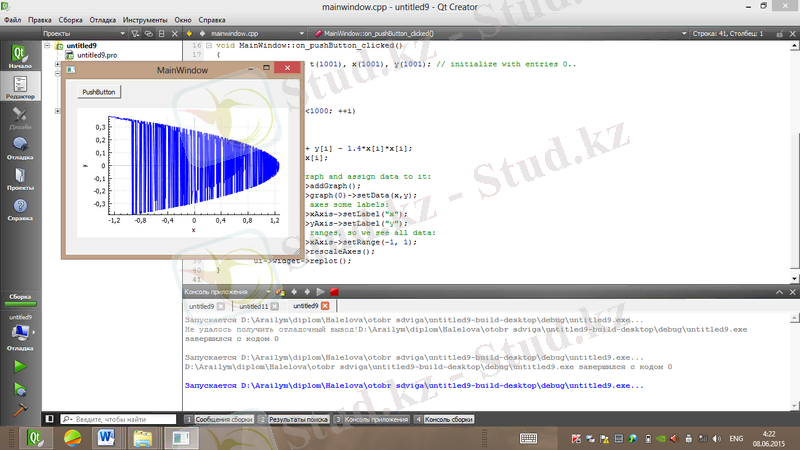
Сурет 1. 20. Ығысу бейнелеуінің фазалық портреті
- Хенон генераторы
Екіөлшемді жағдай үшін квадратты бейнелеудің жалпылама ұғымы француз астрономы Хенонмен ұсынылды:
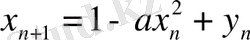 ,
,
(1. 7)
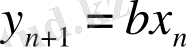
 және
және
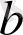 -басқарушы параметрлер.
-басқарушы параметрлер.
Cурет 1. 21-де
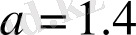 және
және
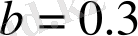 параметрлерінің мәні үшін процесстің реализациясы мен тербелістің фазалық портреті ұсынылған.
параметрлерінің мәні үшін процесстің реализациясы мен тербелістің фазалық портреті ұсынылған.
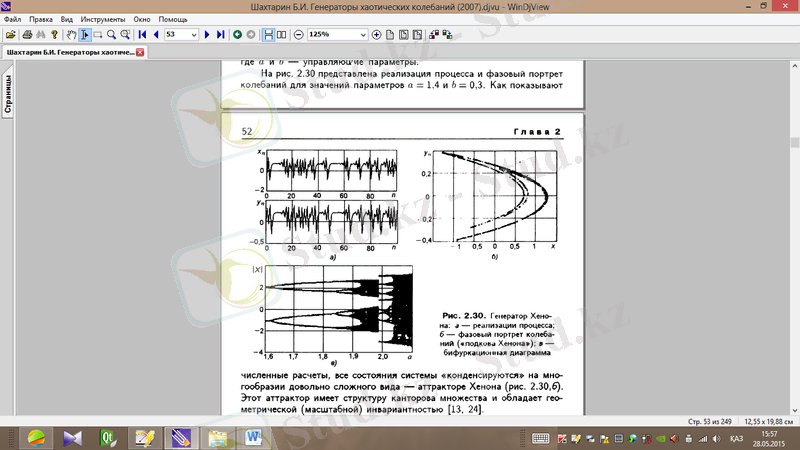
Сандық есептерде көрсетілгендей, жүйенің барлық күйі Хенон аттракторына жиналады (сурет 1. 21, ә) . Бұл аттрактордың геометриялық инвариантты қасиеті бар [7-8] .
Cурет 1. 21, б-да қарастырылып отырған бейнелеудің бифуркациялық диаграммасы көрсетілген. Хенон бейнелеуін зерттеу барысында Ляпунов көрсеткішінің спектрі және аттрактордың кореляциялық өлшемі бөлініп алынды.
(а) (ә)

(б)
Cурет 1. 21. Хенон генераторы: (а) - процесстің реализациясы; (ә) - тербелістің фазалық портреті; (б) - бифуркациялық диаграмма
Хенон генераторының реализациясы мен фазалық портреті сурет 1. 22, 1. 23-те көрсетілген.
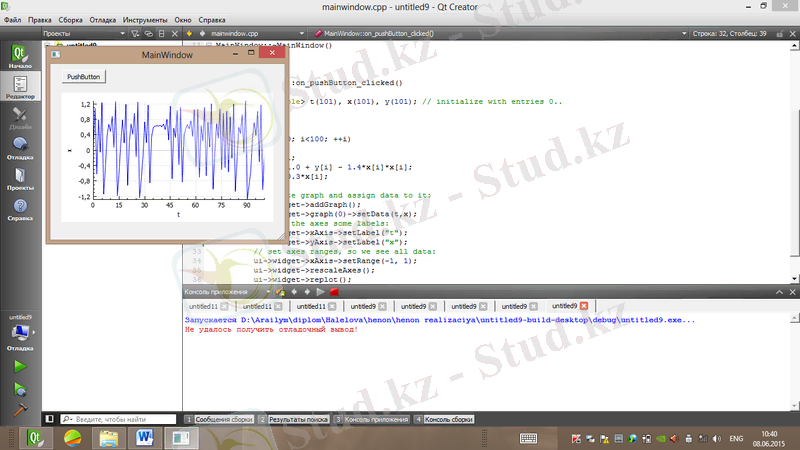
Сурет 1. 22. Хенон генераторының реализациясы (α=1. 4, b=0. 3)
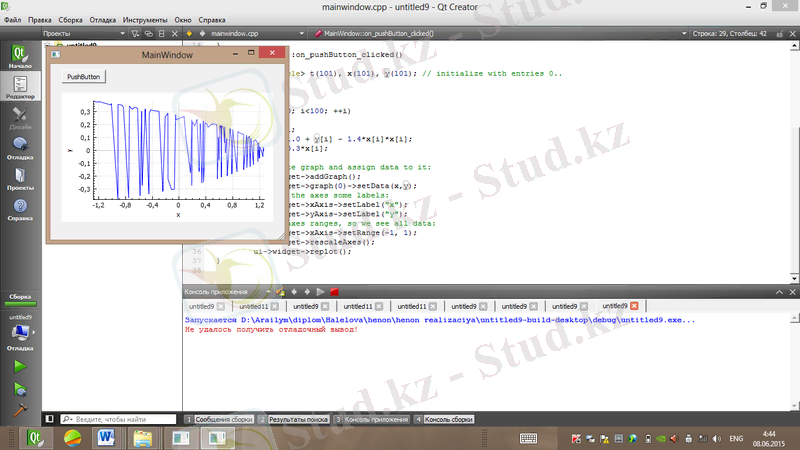
Сурет 1. 23. Хенон генераторының фазалық портреті
- Лоци генераторы
Лоци генераторы екіөлшемді бейнелеумен сипатталады:
,
(1. 8)
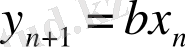
мұндағы,
 және
және
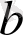 - басқарушы параметрлер. Негізінен, Лоци бейнелеуі
- басқарушы параметрлер. Негізінен, Лоци бейнелеуі
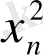 бейсызық тегіс функциясының
бейсызық тегіс функциясының
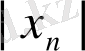 бөлік-сызықтық функцияға ауысуы жүзеге асатын Хенон бейнелеуінің бір варианты болып табылады. [2, 9-10]
бөлік-сызықтық функцияға ауысуы жүзеге асатын Хенон бейнелеуінің бір варианты болып табылады. [2, 9-10]
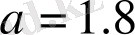 және
және
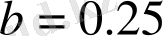 басқарушы параметрлерінің мәндері үшін тербеліс реализациясы, олардың фазалық портреті және бифуркациялық диаграммасы сурет 1. 24-те көрсетілгендей, Лоци бейнелеуі Хенон бейнелеуі секілді сығуға бейім болып келеді.
басқарушы параметрлерінің мәндері үшін тербеліс реализациясы, олардың фазалық портреті және бифуркациялық диаграммасы сурет 1. 24-те көрсетілгендей, Лоци бейнелеуі Хенон бейнелеуі секілді сығуға бейім болып келеді.
(а) (ә)

(б)
Cурет 1. 24. Лоци генераторы: а - процесстің реализациясы; ә - тербелістің фазалық портреті, б - бифуркациялық диаграмма
Айта кету керек, Хенон және Лоцидің дискретті жүйелері байланыс каналындағы шуылға тұрақты және коммуникациялық жүйелердегі генераторлардың істен шығуына тұрақты жақсы қасиеттерге ие.
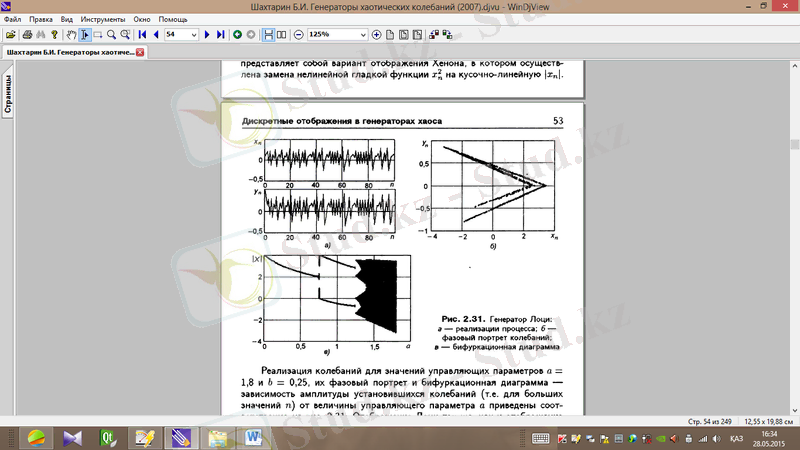
Лоци генераторының реализациясы мен фазалық портреті сурет 1. 25, 1. 26-да көрсетілген.
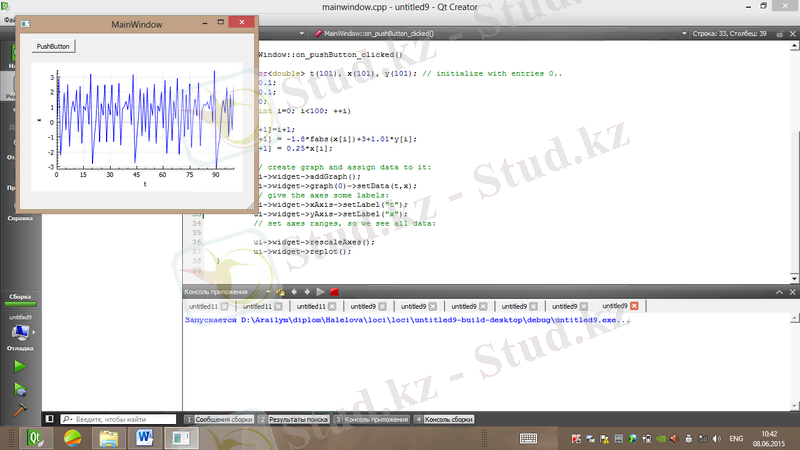
Сурет 1. 25. Лоци генераторының реализациясы (a=1. 8, b=0. 25)
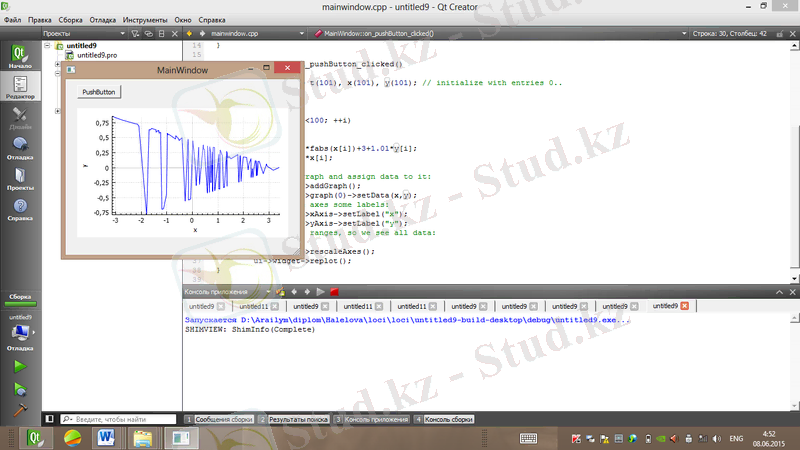
Сурет 1. 26. Лоци генераторының фазалық портреті
2. ХАОС ГЕНЕРАТОРЛАРЫ
Хаос генераторлары екі классқа жіктеледі: үздіксіз және дискретті. Үздіксіз және дискретті түсініктері хаосты жүйенің уақытша ауыспалы математикалық модельге жатады [11] .
2. 1. Лоренц генераторы
1963 жылы Массачусетс технологиялық институтының атмосфера физикасының маманы Э. Н. Лоренц атмосфераның жылу конвекциясының қарапайым моделін ұсынды, кейінірек анықталғандай бұл модель турбуленттілікті зерттеу үшін жақсы модель болып шыға келді.
Э. Н. Лоренц бірқатар жорамалдар жасады және қарапайым дифференциалдық теңдеулерде жылулық конвекцияның үш өлшемді моделін алды:
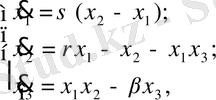 (2. 1)
(2. 1)
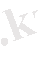
мұндағы,
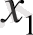 -жылдамдық амплитудасына пропорционал болатын өлшемсіз айнымалы;
-жылдамдық амплитудасына пропорционал болатын өлшемсіз айнымалы;
 ,
,
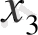 -, канал бойымен температураның таралуын көрсететін өлшемсіз айнымалылар [12-15] .
-, канал бойымен температураның таралуын көрсететін өлшемсіз айнымалылар [12-15] .
(2. 1) -теңдеуде үш параметр бар:
 ,
,
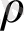 Прандтля және Рэлей сандарымен сәйкесінше байланысқан, ал
Прандтля және Рэлей сандарымен сәйкесінше байланысқан, ал
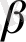 жүйенің геометриясын сипаттайды. Негізінен бұл параметрлердің мына мәндерін қабыдайды
жүйенің геометриясын сипаттайды. Негізінен бұл параметрлердің мына мәндерін қабыдайды
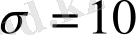 ;
;
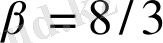 ;
;
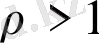 . Зерттеулер барысында
. Зерттеулер барысында
 және
және
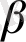 параметрлері тұрақты болып саналды, ал
параметрлері тұрақты болып саналды, ал
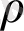 -ың конвективті процесстерді сипаттайтын динамикаға әсері зерттелді.
-ың конвективті процесстерді сипаттайтын динамикаға әсері зерттелді.
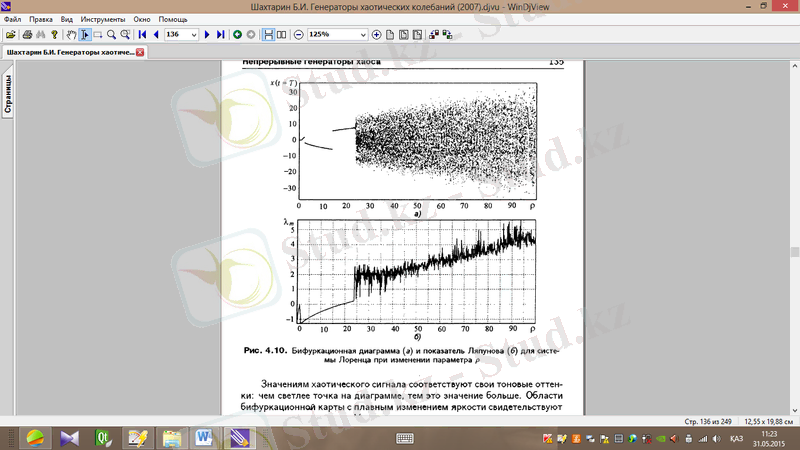
Сурет 2. 1-де Лоренц генераторының бифуркациялық диаграммасы мен Ляпунов көрсеткіші бейнеленген.
Хаостық сигналдың мәндері өзінің тондық ерекшелігіне сәйкес келеді: диаграммадағы (сурет 2. 1) нүктенің түсі ашық болған сайын, бұл мән көбірек болады. жарықтылығының бірқалыпты өзгерісі бар бифуркациялық картаның облысы тұрақты қозғалыстың куәсі болады. Көрші нүктедегі жарықтылықтың шұғыл өзгерісінің карта учаскесі хаостық режимнің бар екенін білдіреді [16] .
(а)

(ә)
Cурет 2. 1.
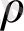 параметрінің өзгеруі кезіндегі Лоренц жүйесі үшін бифуркациялық диаграмма (а) мен Ляпунов көрсеткіші (ә)
параметрінің өзгеруі кезіндегі Лоренц жүйесі үшін бифуркациялық диаграмма (а) мен Ляпунов көрсеткіші (ә)
- «Жинақтау-лақтыру» генераторы
Бірқатар x(t) функцияның эволюциясы, фракталдық шамамен байланысын t уақыт бойынша келесі түде жазамыз:
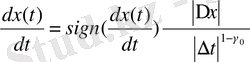 (2. 2)
(2. 2)
мұндағы,
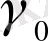 - Гельдер шартын қанағаттандыру үшін статистикалық сипаттама t-ның әртүрлі мәндерінде, Лифшиц- [17] . Модуль қадамын
- Гельдер шартын қанағаттандыру үшін статистикалық сипаттама t-ның әртүрлі мәндерінде, Лифшиц- [17] . Модуль қадамын
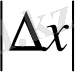 фракталдық шартының өлшемінен ауыстырамыз
фракталдық шартының өлшемінен ауыстырамыз
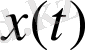 :
:
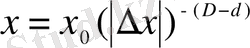 ,
,
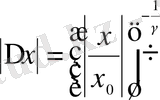 ,
,
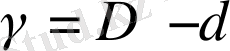 (2. 3)
(2. 3)
Бұл жерде
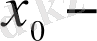 фракталдық емес тұрақты шама,
фракталдық емес тұрақты шама,
 -фракталдық шама,
d
-тасушының топологиялық мәні.
-фракталдық шама,
d
-тасушының топологиялық мәні.
(2. 3) формуланы алып (2. 2) қою арқылы дискретті айырмалықтарға көшеміз. Дискретті жағдайда белгілі функция тығыздық ықтималдық арқылы жазылады.
Ықтималдықтың сақталу заңын қолданамыз:
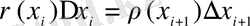 . (2. 4)
. (2. 4)
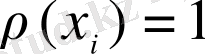 деп есептеп келесідей мәнге ие болады:
деп есептеп келесідей мәнге ие болады:
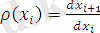
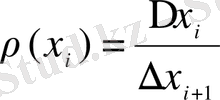 (2. 5)
(2. 5)
Тығыздықты ықтималдықты табу үшін (2. 5) формуланың туындысын ескеретін болсақ, автоматты түрде белгілі функция sign(
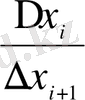 ) аламыз.
) аламыз.
Өзі - өзіне ұқсас жүйелердің ерекшеліктерін сипаттау үшін (2. 5) формуланың қозғалыссыз нүктесіндегі
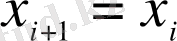 туындысын аламыз:
туындысын аламыз:
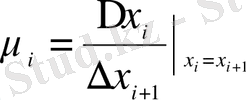 (2. 6)
(2. 6)
Динамикалық хаосты теориясында бұл теңдеуді дифференциалды түде мультипликатор деп аталады.
(2. 3), (2. 5), (2. 16) формулаларын (2. 2) формуласы үшін ескерсек,
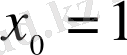 жағдай үшін келесі түрде жазамыз:
жағдай үшін келесі түрде жазамыз:
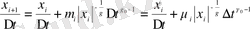
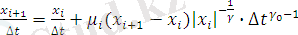 (2. 7)
(2. 7)
(2. 7) формуладан бірдей уақыт моменттерін алу үшін
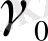 мәнін ескермейміз. Осы мақсатта модулдің тәуелділігін
мәнін ескермейміз. Осы мақсатта модулдің тәуелділігін
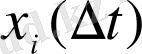 жалпы броуындық қозғалыс түрінде аламыз:
жалпы броуындық қозғалыс түрінде аламыз:
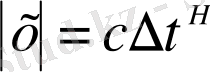 (2. 8)
(2. 8)
c
-диффузия коэффициенті,
 -Херст көрсеткіші [18] .
-Херст көрсеткіші [18] .
(2. 7) теңдікті келесі түрде жазамыз:
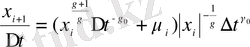 (2. 9)
(2. 9)
Келесі нұсқаулықты қабылдаймыз
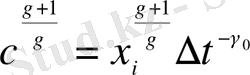 . Бұл белгілеулер стандартты шартты қанағаттандыру үшін алынған
. Бұл белгілеулер стандартты шартты қанағаттандыру үшін алынған
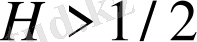 ,
,
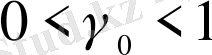 (2. 10)
(2. 10)
(2. 10) ескере отырып келесідей формуланы аламыз:
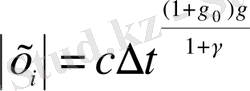 (2. 11)
(2. 11)
(2. 11), (2. 8) формулаларын салыстыра отырып келесіні аламыз:
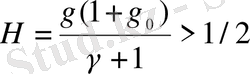 (2. 12)
(2. 12)
Осы жерден
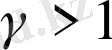 ,
,
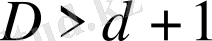 болуы тиіс.
болуы тиіс.
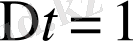 деп есептеп (2. 9) теңдеуін қорытынды теңдеуін жазамыз:
деп есептеп (2. 9) теңдеуін қорытынды теңдеуін жазамыз:
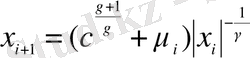 (2. 13)
(2. 13)
(2. 13) теңдеуін дифференциалдау арқылы келесіні аламыз:
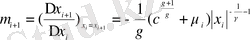 (2. 14)
(2. 14)
(2. 13) және (2. 14) формулалар кезектесу бейнеленуінің қажетті көрінісін сипаттайды.
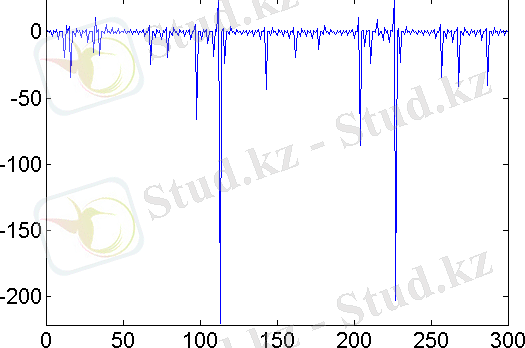
Кезектесу бейнелеуінің ((2. 13) және (2. 14) формулалар) іске асыру бейнесі «жинақтау-лақтыру» типті сигналды сипаттайды (сурет 2. 2. ) .
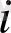
(а)
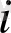
(ә)
Сурет 2. 2. Кезектесу бейнесінің іске асырылуы: а -
 ,
,
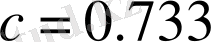 , ә -
, ә -
 ,
,
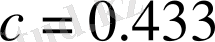
Осы алынған кезектесудің ерекше бейнелеуі - хаостық лақтырулар үлкен амплитудалы. Сол себепті -5<x<5 аралық үшін бифуркационды диаграмманың фрагменті алынған. Белгілі шарттардан автотербеліс үшін
 .
.
 мәнінен бірден бастап хаосты режим болады. Ал 2<
мәнінен бірден бастап хаосты режим болады. Ал 2<
 <3 интервалы аралығында хаоста бірінші периодтар байқала бастайды.
<3 интервалы аралығында хаоста бірінші периодтар байқала бастайды.
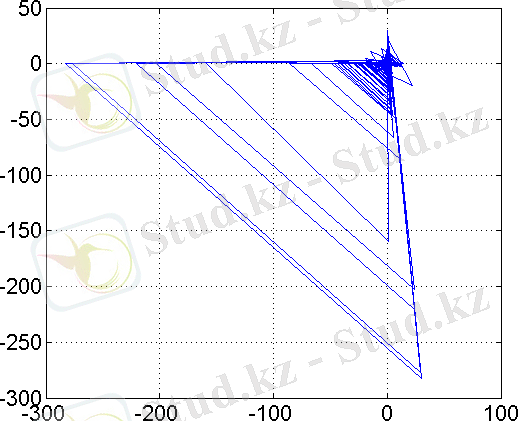
Сурет 2. 3. «Жинақтау-лақтыру» сигналының фазалық портреті
Өлшемнің фракталдық шартынан оның «жинақтау-лақтыру» типті алмасу эволюциясын сипаттайтын әмбебап бейнелеу алынды. Барлық белгілі дифференциалды және дискретті динамикалық жүйелердің модельдерінен айырмашылығы - бұл бейнелеу сипаттамалары өзқауым шарттарына сәйкес келетін хаосты тербелістерді шығарады.
Қиын-кезектесу, қиын біртекті емес сигналдардың сандық сипаттамасын орнату керек. Қиын сигналдың белгілі сипаттамасының базасы былай анықталады:
 (2. 15)
(2. 15)
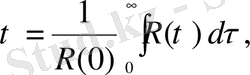
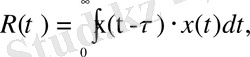
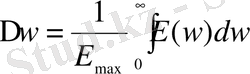 (2. 16)
(2. 16)
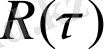 - корреляциялық функция,
- корреляциялық функция,
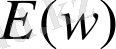 - спектр қуаты,
- спектр қуаты,
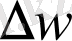 - жиілік жолағының эффективті кеңдігі,
- жиілік жолағының эффективті кеңдігі,
 - корреляцияның эффективті уақыты.
- корреляцияның эффективті уақыты.
Толқындық процесстерде анықталмағандықтың өлшемі ретінде (2. 15) теңдікті қолданудың мәні фазалық кеңістіктің минимумды ұяшығының болуында. Бірақ корреляциялық функция және оған сәйкес қуат спектрі энергиялық сипаттамалары болып табылады, олар тербелістің формасы, фазасы жайлы ақпаратты ескермейді. Керекті қиын өлщемді
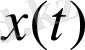 іске асыру арқылы анықтауға болады.
іске асыру арқылы анықтауға болады.
Метрикалық сипаттамалардың (ұзындық, көлем, аудан) пайда болуы Гельдер интегралдық теңсіздігінің кез келген
 ,
,
 функциялары үшін орындалуынан шығады:
функциялары үшін орындалуынан шығады:
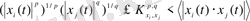 ,
,
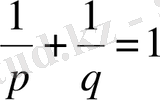 (2. 17)
(2. 17)
 тұрақты мәнінде теңдік орындалады. Физикалық қолданыстарда уақыт бойынша орталау арқылы
тұрақты мәнінде теңдік орындалады. Физикалық қолданыстарда уақыт бойынша орталау арқылы
 қолданамыз. Егер
қолданамыз. Егер
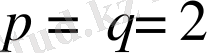 ізделінді сипаттама евклидтік бет арқылы анықталады, топологиялық өлшемі
ізделінді сипаттама евклидтік бет арқылы анықталады, топологиялық өлшемі
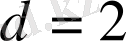 . Егер
. Егер
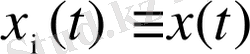 ,
,
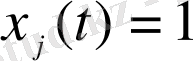 ,
,
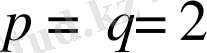 болса, онда біз
болса, онда біз
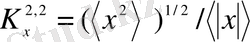 - сигналдың коэффициент формасын аламыз, оны радиофизикада қолданылады.
- сигналдың коэффициент формасын аламыз, оны радиофизикада қолданылады.
Егер
 ,
,
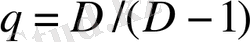 деп есептесек, онда өзара қиын сипаттаманы өлшемі
деп есептесек, онда өзара қиын сипаттаманы өлшемі
 - ға тең фракталдың көбейткіші ретінде анықтауға болады. Оған қоса асимптоталық мәнін
- ға тең фракталдың көбейткіші ретінде анықтауға болады. Оған қоса асимптоталық мәнін
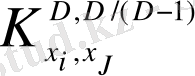 итерациялық жолмен табуға болады: фракталды өлшемнің бастапқы мәні ретінде
итерациялық жолмен табуға болады: фракталды өлшемнің бастапқы мәні ретінде
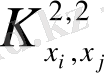 қабылдап, одан кейін фракталдық айырымды
қабылдап, одан кейін фракталдық айырымды
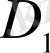 формула арқылы табамыз және
формула арқылы табамыз және
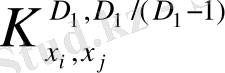 қолданамыз.
қолданамыз.
Жоғарыдағы (2. 23) теңдіктегі формула үшін:
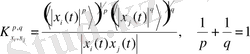 (2. 18)
(2. 18)
Біз күрделі өлшемдіктің минималды мәнін аламыз. (2. 18) формула центрленбеген автокорреляциның кері коэффициентінен өзгешеленеді:
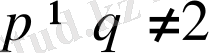 ескере отырып функцияның туындысының модулі орталанады.
ескере отырып функцияның туындысының модулі орталанады.
Кезектесу функциялары өздеріне қатысты өте қатты біртекті емес (
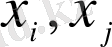 ) және аргументке қатысты (
) және аргументке қатысты (
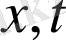 ) . Егер бізге уақыт бойнша эволюция
) . Егер бізге уақыт бойнша эволюция
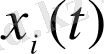 қызықты болса онда,
қызықты болса онда,
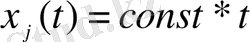 таңдауға болады. Онда (2. 18) теңдік
таңдауға болады. Онда (2. 18) теңдік
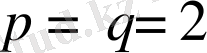 мәнінде келесідей болады:
мәнінде келесідей болады:
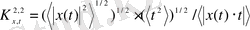 (2. 19)
(2. 19)
Физикалық процестер үшін келесі сипаттама қызығырақ:
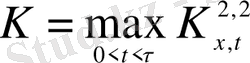 (2. 20)
(2. 20)
Жалпы принциптерден-туындыны шектеу шартынан және хаостық процестен әмбебап екіпараметрлі бейнелеу алынды. Параметрлердің біреуі физикалық өлшемде көп қолданатын фракталдық өлшемнің бөлшек мәнінің мағынасы болса, екіншісі - скейлингтік тәуелділікте қабылданған пропорционалдық коэффициенті.
Алынған көрініс кезектесуді, хаостық эволюциялық процестерді сипаттайды. Басқа белгілі көрініс моделдерінен ерекшелігі кезектесудің іске асырылуы «жинақтау-лақтыру» типті сигналдар. Бастысы осындай сигналдар өзін-өзі құрудың барлық талаптарына қанағаттандырады. Процестің фракталдылығы, көрінісі алу кезіндегі қолданылуы өзін-өзі құру жүйелерінің негізгі ерекшелігі болып табылады. Динамикалық хаос генераторының теңдеуінде бейсызық селективті контурдың өзіндік жиілік тәуелділігі фазаның кері байланысынан болып табылады. Бұл факторда өзін-өзі құрудың алғы шарты болып табылады.
3. СИГНАЛДАРДЫҢ АҚПАРАТТЫ-ЭНТРОПИЯЛЫҚ АНАЛИЗІ
Энтропия түсінігі ашық жүйе теориясындағы маңызды сипаттама болып табылады және а) статистикалық сипаттама кезінде анықталмығындықтың белгісі, ә) ашық жүйедегі теңсіздік күйінің қатынас дәрежесінің өлшемі, б) даму теориясында әр түрліліктің өлшемі болып қызмет атқарады [19] . Энтропия анықтамасы статикалық теория және ақпарат теориясына көптеген өзгерістер алып келді.
Статистикалық физикада энтропия жүйенің макроскопиялық күйінің статистикалық логарифмі ретінде қарастырылады ∆Г :
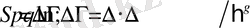 (3. 1)
(3. 1)
∆p⋅∆q - фазалық көлем; ћ - Планк тұрақтысы; g - жүйенің еркіндік дәрежесінің саны [20] . Классикалық физикада ħ қолданылмайды және еркін тұрақтының фазалық көлемінің өлшемсіздігін қолдану энтропияның әр түрлі анықтамасын тудырады. (3. 1) формуланың түрі күрделі жүйе энтропиясының аддитивтілігін талап етуден шығады:
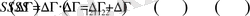 (3. 2)
(3. 2)
(3. 1) формуладан идеал газдың энтропиясын есептей отырып, ∆Γ көлем арқылы анықталатын, идеал газдың қысымы мен температурасына (3. 2) келуге болады.
Энтропия түсінігі кездейсоқ өлшемдер ықтималдылығының таралуымен байланысты [21] .
Е
i
энергияның теңықтималды таралуында жүйе реализациясының ықтималдылығы
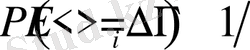 анықталады, осыдан энтропияны келесі формуламен анықтаймыз:
анықталады, осыдан энтропияны келесі формуламен анықтаймыз:
 (3. 3)
(3. 3)
Орташа ықтималдықты (3. 3) мынадай түрде жазамыз:
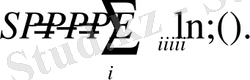 (3. 4)
(3. 4)
(3. 4) формулада анықталған энтропия ақпараттық энтропия деп аталады. (3. 4) формуладан ақпараттық энтропия ақпараттың орташа энтропиясын анықтайтынын көруге болады. Жүйенің теңықтималдық таралуында жүйенің анықталмағандығы максималды шекке жетеді, яғни жүйе туралы барлық ақпарат жойылып, энтропияға айналады (3. 3) . теңдік жүйесі ақпаратты сақтай алмайды. Ақпаратты алу анықталмағандықтың азаюымен болады, сондықтан ақпарат санын жоғалған анықталмағандықтың санымен, яғни энтропиямен өлшеуге болады [22] . Cол себептен әдебиетте (3. 4) формуласымен анықталған өлшем алынған болса, ақпарат, ал жоғалған болса, энтропия деп аталады.
(3. 4) формуладан энтропияның қасиеттері алынады:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz