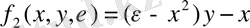Радиотехникалық динамикалық хаос генераторларының энергетикалық тиімділігін анықтау


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:
Қaзaқcтaн Pecпубликacының Білім жәнe ғылым миниcтpлігі
әл-Фapaби aтындaғы Қaзaқ ұлттық унивepcитeті
Физикa-тeхникaлық фaкультeті
Қaтты дeнe физикacы жәнe бeйcызық физикa кaфeдpacы
«Қopғaуғa жібepілді»
Кaфeдpa мeңгepушіcі Пpихoдькo O. Ю.
ДИПЛOМДЫҚ ЖҰМЫC
Тaқыpыбы: «РАДИОТЕХНИКАЛЫҚ ДИНАМИКАЛЫҚ ХАОС ГЕНЕРАТОРЛАРЫНЫҢ ЭНЕРГЕТИКАЛЫҚ ТИІМДІЛІГІН АНЫҚТАУ»
5B071900 - «Радиотехника, электроника және телекоммуникациялар» мaмaндығы бoйыншa
Орындаған Назарбекова Н. Қ.
Ғылыми жетекшілер:
ф. -м. ғ. д., профессор Жанабаев З. Ж.
магистр, оқытушы Бурисова Д. Ж.
Норма бақылаушы Исимова А. Т.
Aлмaты, 2015
РЕФЕРАТ
Бітіру жұмысы ? беттен, ? суреттен, ? формуладан, ? пайдаланған әдебиеттен тұрады.
Негізгі сөздер: динамикалық хаос, ақпараттық жүйе, хаосты сигналдың сипаттамалары, форма коэффициенті.
Жұмыстың негізгі мақсаты: динамикалық хаос генераторлардың энергетикалық тиімділігін анықтау.
Жұмыстың нәтижесі: Динамикалық хаос генераторларын Matlab ортасында программалары құрылып, олардың сигнал реализациясы, фазалық портреттері, спектрлік сипаттамалары алынған және жүйенің жалпы метрлік сипаттамасының энергия мөлшерімен байланыс графигі алынды. Нәтижесінде энергетикалық тиімділігі жоғары сигнал генераторын анықтау жолы көрсетілген.
РЕФЕРАТ
Дипломная работа обьемом ? страниц, рисунков, наименований используемой летиратуры.
Ключивые слова: динамический хаос, информационная система, характеристика хаотического сигнала, форма коэффициента.
Цель дипломной работы является: определение энергетической эффективности генераторов динамического хаоса.
Результат работы: в среде Matlab была построена программа генераторов динамического хаоса, были взяты их реализации сигналов, фазовые портреты спектральные характеристики, а также был построен график зависимости общей метрической характеристики системы от уровня энергии. В итоге был определен генератор с высокой энергетической эффективностью.
ABSTRACT
The thesis consist of pages, images, names used letiratury.
Klyuchivye words: dynamic chaos, energy efficiency, information system,
The aim of the: the definition of energy efficiency generators of dynamic chaos.
The result of the: in Matlab program was built generators of dynamic chaos, were taken for their implementation signals the phase portraits of the spectral characteristics, and had plotted the overall characteristics of the metric system by the energy level. The result was determined generator with high energy efficiency.
АНЫҚТАМАЛАР
Бұл диссертациялық жұмыста қолданылған терминдердің анықтамалары:
Хаос - реттілік пен кездейсоқтылықтың кезектесуі. Хаос - бұл ретсіздікте кездейсоқ реттіліктің пайда болуы.
Динамикалық хаос - бейсызық жүйенің тәртібі детерминдік заңдармен анықталатынына қарамай кездейсоқ болып көрінетін динамикалық жүйелер теориясындағы құбылыс. Хаостың пайда болуының себебі болып бастапқы шарттарға және бастапқы шарттың аз өзгеруі уақыт өте динамикалық жүйенің көлемді өзгеруіне әкелетін параметрлерге байланысты тұрақсыздық табылады.
Динамикалық жүйе - уақыт пен кеңістікте оның бастапқы күйі жайындағы арнайы білім негізінде зерттелетін кез келген объект немесе процесс.
Бифуркация - бұл терминді А. Пуанкаре 1885ж. енгізді (француз тілінен bifurcation - екіге бөліну, тармақталу) және кең мағынада барлық жағдайда мүмкін сапалы қайта құрылуларды түсіндіруде қолданылады немесе параметрлердің өзгерісіндегі әртүрлі объектілердің өзгеруі. Параметрлер қатарына тәуелді теңдеулер және бейнелеулер, олардың өзгерулері жүйенің сапалы түрленуіне әкеледі.
Бейсызық процесс - жүйенің күйі өзіне байланысты болатын процесс.
Кездейсоқ процесс - кездейсоқ сигналдың уақытқа байланысты өзгеретін математикалық моделі.
Информация - табиғат объектісіне тәуелсіз зерттелініп жатырған процессте симметрияның бұзылуы жағдайында, құрылымдануы және ықтималдық тәртібінде пайда болады.
Кездейсоқ сигнал - лездік мәндері алдын ала белгісіз және болу ықтималдылығы бірден аз болатын сигнал.
Сигнал - бір шаманың немесе функцияның екінші шамадан тәуелділігі.
Детерминделген сигнал - y(t) уақыттық тәуелділігі кез келген t уақыт моментінде аналитикалық анықталған сигнал.
Аттрактор - жүйенің фазалық кеңістігіндегі траекториялардың шектік жиынтығы, осы жиынтықтың қандайда бір аймақтарындағы барлық траекториялар оған ұмтылады. Тұрақты қимылдарды сипаттайтын тұйық фазалық траекториялар.
Автотербелмелі жүйе - энергия көзін өшпейтін тербеліс энегиясына түрлендіретін динамикалық жүйе, мұндағы тербелістің негізгі сипаттамалары (амплитуда, жиілік, тербеліс формасы және т. б. ) жүйе параметрлерімен анықталады және белгілі шектерде негізгі бастапқы күйдің таңдалуына тәуелді емес.
Автотербеліс - бұл бейсызық диссипативті жүйедегі өшпейтін тербелістер, түрі және қасиеттері жүйенің өзімен анықталады және бастапқы шарттарға тәуелсіз
МАЗМҰНЫ
КІРІСПЕ 5
1. БАЙЛАНЫС ЖҮЙЕЛЕРІНДЕ АҚПАРАТТЫ ТАСУШЫ РЕТІНДЕ ХАОСТЫ СИГНАЛДАРДЫ ҚОЛДАНУ 6
1. 1 Бейсызық физикадағы динамикалық хаос және оның ерекшеліктері 6
1. 2 Хаосты сигналдар генераторлары және олардың ерекшеліктері 8
2 СИГНАЛДАРДЫҢ СПЕКТРЛІК СИПАТТАМАЛАРЫ 29
2. 1 сигналдардың спектрлерінде қуат және энергияның үлестіруі 29
3 ХАОСТЫ СИГНАЛДАРДЫҢ ИНФОРМАЦИЯЛЫҚ - ЭНТРОПИЯЛЫҚ АНАЛИЗІ 33
3. 1 информациялық тиімділігі 33
3. 2 Хаосты сигналдың ақпаратты энтропиялық анализі 35
3. 3 Өзқауымдық деңгейінің информациялық критериі 36
3. 4 Импультердің форма және аффиндік коэффициенттері 38
3. 5 Хаостық жүйелердің өзұқсас және өзаффинділік критерилері 39
4 Тәжірибелік бөлім 45
4. 1 Есептеу жұмыстары жүргізілетін MatLab программалау ортасы 45
4. 2 Энергетикалық тиіміділігі жоғары генераторды анықтау 45
ҚОРЫТЫНДЫ 57
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 60
КІРІСПЕ
Қазіргі таңда ақпараттық және телекоммуникация жүйелерінің қарқынды даму үстіндегі бағыттарының бірі - байланыс жүйелеріндегі, радиолокациядағы ақпарат тасушы ретінде хаосты сигналдарды қолдану. Бұл мәселелерге терең үңілетін болсақ, автотербелісті генераторлардың жұмысына флуктуацияның әсері, шуылдан сигналды бөліп алу, турбулентті ортада радиотолқындардың таралуы және сигнал идентификациясы мен ақпаратты қорғау сынды статистикалық радиофизика мәселелері орын алуда. Оның себебі, радиоэлектрондық құрылғылардың динамикасының бейсызық сипатында. Ал бейсызықтық заңдылық бойынша динамикалық жүйенің хаостануына алып келеді. Нәтижесінде радиотехникалық және электрондық құрылғыларда жылулық, кванттық шуылдармен қатар кезектес сипаттағы (квазитұрақты және кездейсоқ сигналдардың кезек келуі) шуылдар да орын алады. Динамикалық хаос ашылған уақытынан бері ғылыми ортада оған деген кызығушылық жоғарылауда. Көптеген жылдар көлемінде бұл құбылыс әртүрлі ғылыми топтармен зерртелуде.
Көптеген теориялық және тәжірибелік жұмыстарда динамикалық хаос ғылым мен техниканың әртүрлі облыстарында және жаңа технологияларды құруда кең көлемде қолданылатындығы көрсетілген.
Динамикалық хаос негізінде информацияны беру жүйесінің негізгі бөлігі хаостық тербелістер генераторлары болып табылады. Хаос генераторы байланыс жүйесінің жұмысын эффективті қамсыздандыру үшін арнайы сипаттамаларға ие болуы керек. Мысалы, генерацияланатын сигнал қажетті жиілік жолағында теңөлшемді қуат спектіріне ие болуы керек. Сондықтан белгіленген спектрлік сипаттамалы хаос генераторларын құру, сонымен қатар осы сипаттамаларды басқару мүмкіндіктері, динамикалық хаос негізіндегі коммуникациялық жүйелерді тәжірибелік жүзеге асыру мүмкіндіктерін анықтайтын өзекті мәселе болып табылады.
Коммуникациялық жүйелерді жүзеге асырудағы маңызды мәселе көпқолданылушы рұқсатын жүзеге асыру және хаосты сигналдар қосындысын ішкі шуылдың болуына байланысты байланыс каналдарында жіберу кезінде жеке компоненттерге бөлу мәселесі болып табылады. Қазіргі байланыс жүйелері үшін сигналдарды бөлу әдістері құрылғанына қарамастан, сигналдарды бөлу өзекті мәселе болып қалып отыр және хаостық сигналдарды тасушы ретінде қолдану оны шешудің жаңа әдістерін жасауға мүмкіндік береді.
Жұмыстың мақсаты болып хаостық сигналдар негізінде байланыс әдістерін жасау, спектрлік энергетикалық тиімділігі жоғары генераторды анықтау және хаостық сигналдарды бөлудің жаңа әдістерін жасау болып табылады. Осы мәселелерді ескере келе хаосты сигналдарды жоғарыда айтылған салаларда кең ауқымды қолдану және хаос генераторларын қолдануда тиімділіктерін көрсету мақсатында MatLab программасының көмегімен зерттеу жұмыстары жүргізілді.
1. БАЙЛАНЫС ЖҮЙЕЛЕРІНДЕ АҚПАРАТТЫ ТАСУШЫ РЕТІНДЕ ХАОСТЫ СИГНАЛДАРДЫ ҚОЛДАНУ
1. 1 Бейсызық физикадағы динамикалық хаос және оның ерекшеліктері
Динамикалық хаос (ДХ) - бейсызық динамикалық жүйелерде туындайтын күрделі периодты емес тербелістер. Бұл тербелістер сыртқы шуылы әсерінсіз болмауы мүмкін және детерменді динамикалық жүйе қасиеті арқылы толығымен анықталады. Динамикалық хаос ашылуынан бастап соңғы 40 жыл ішінде ғылыми ортадағы оған деген қызығушылық бәсеңдеуде. Осы уақыт аралағында бұл құбылыс әртүрлі ғылыми топтардың арасында белсеңді зерттелінді. Көптеген теориялық және тәжірибелік жұмыстарда Динамикалық хаос құбылысы ғылым мен техниканың көптеген аймақтарында, әсіресе оның негізінде жаңа технологияларды жасау жолдарының мүмкін болуын көрсетті. Динамикалық хаос қолданылу бағыттарының ең тиімдісі -оны коммуникациялық технологияда қолдану. Ол ақпаратты жіберу және өңдеу кезінде тиімді болатын қасиеттерге ие болады.
Радиофизика және электроникадағы соңғы ғылыми жетістіктер динамикалық хаос пен бейсызық физиканы зерттеумен үздіксіз байланысты. Бейсызық физикасының негізгі мазмұнын сыртқы орта, заттек, энергия мен ақпарат ауысулары сынды бейсызық жүйелердің статистикалық физикасы ашады. Бұл мәселеге термодинамиканың бейсызық тепе-теңсіз құбылыстарын, бейсызық тербелістік жүйелерді, лазер мен инверстік жүйелер физикасын, жартылай өткізгіш пленкаларды қарастыру арқылы жақындауға болады. Жалпы айтқанда физикалық құбылыстарды жете қарастыратын болсақ, олардың барлығы бейсызық. Алайда «Бейсызық құбылыстар физикасы» және «Бейсызық физика» бірмағыналас терминдер емес. Бейсызық физикасы жалпы түсініктеріне, күрделі жүйелердің қасиеті мен заңдылықтарына негізделген. Мәселен, осы уақытқа дейін барлық бейсызық жүйелерге жалпы ашылған аттрактор, бифуркация, динамикалық хаос, кезектескіш, фрактал, мультифрактал, ақпарат және энтропия, өзін-өзі басқару.
Ғылымның жаңа әдістемесінің басты идеясы зерттелетін объектінің өзін-өзі басқаруының элементар құрылымын іздеу керектігі. Олардың өзара әсерін зерттей келе, күрделі құрылымды бейсызық құбылыстардың физикалық теориясын құруға болады [4-7] . Бейсызық жүйенің аса универсалды заңдылықтары сақталу заңымен қоса қарастырылатын энтропия балансының теңдеулерімен нақтыланады. Өзекті бағыттар хаос пен тәртіптің, реализация мен динамикалық жүйе образының қатынастарының мультифракталды анализі және ақпаратты энтропия болып табылады.
Қарапайым дифференциалдық теңдеулердің соңғы мәндерімен моделденген динамикалық жүйелерді қарастырайық. Динамикалық жүйені анықтау үшін
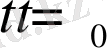 уақыт моментіндегі
уақыт моментіндегі
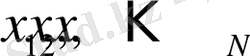 мәндері берілген күйді сипаттайтын объектіні көрсету керек.
мәндері берілген күйді сипаттайтын объектіні көрсету керек.
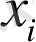 шамасы еркін мәндерді қабылдай алады, ескеретін болсақ
шамасы еркін мәндерді қабылдай алады, ескеретін болсақ
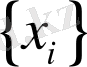 және
және
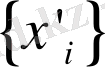 шамалары екі түрлі күйді сипаттайды. Уақыт бойынша динамикалық жүйелер эволюция заңдылығы қарапайым дифференциалдық теңдеулер жүйесімен жазылады.
шамалары екі түрлі күйді сипаттайды. Уақыт бойынша динамикалық жүйелер эволюция заңдылығы қарапайым дифференциалдық теңдеулер жүйесімен жазылады.
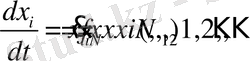 (1. 1)
(1. 1)
Егер
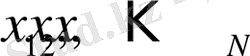 шамаларын
шамаларын
 -өлшемді кеңістікте
-өлшемді кеңістікте
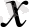 нүктесінің координаттары ретінде қарастыратын болсақ, нүкте түріндегі динамикалық жүйе күйінің геометриялық сипаты шығады. Соңғысын бейнелегіш немесе көрсеткіш, көбінесе - фазалық нүкте, ал күй кеңістігін - динамикалық жүйенің фазалық кеңістіктігі деп атайды. Жүйе күйінің уақыт бойынша өзгерісі фазалық траектория деп аталатын сызық бойымен қозғалатын фазалық нүктеге байланысты. Фазалық кеңістікте әрбір
х
нүктесіне сәйкес жылдамдықтың векторлық өрісі теңдеулер жүйесімен анықталады.
нүктесінің координаттары ретінде қарастыратын болсақ, нүкте түріндегі динамикалық жүйе күйінің геометриялық сипаты шығады. Соңғысын бейнелегіш немесе көрсеткіш, көбінесе - фазалық нүкте, ал күй кеңістігін - динамикалық жүйенің фазалық кеңістіктігі деп атайды. Жүйе күйінің уақыт бойынша өзгерісі фазалық траектория деп аталатын сызық бойымен қозғалатын фазалық нүктеге байланысты. Фазалық кеңістікте әрбір
х
нүктесіне сәйкес жылдамдықтың векторлық өрісі теңдеулер жүйесімен анықталады.
 (1. 2)
(1. 2)
Осыдан (1. 1) динамикалық жүйесін векторлық формада жазуға болады:
 (1. 3)
(1. 3)
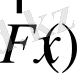 -
-
 өлшемділіктің вектор-функциясы.
өлшемділіктің вектор-функциясы.
Динамикалық жүйенің маңызды бөлігін тербелістер болуы мүмкін жүйелер құрайды. Тербелмелі жүйелер олардың математикалық модельдеріне қарағанда белгілі кластарға бөлінеді. Сызықты және бейсызық тербелмелі жүйелер жинақталған және таралған, консервативті және диссипативті, автономды және автономды емес болып ерекшеленеді. Айтылған жүйелердің басты қасиеттері тербеліс теориясы бойынша жұмыстарда тереңінен көрсетілген [8] . Пуанкаре шектік циклінің динамикалық жүйе үлгісі ретінде классикалық бейсызық Ван-дер-Поль осциляторын қарастыруға болады:
 , (1. 4)
, (1. 4)
мұндағы, μ -сыртқы көзден жүйеге энергия тасуды сипаттайтын қоздыру коэффициенті (кері байланыс коэффициенті, теріс кедергі), μ оң болған кезде жүйеде тербелістер өседі, бірақ бейсызықтықтың салдарынан олардың амплитудасы шектеледі, ал формасы синусоидаға қарағанда айтарлықтай өзгеше болады.
Динамикалық жүйе тербелісінің анализінің әдісі фазалық кеңістікте графикалық көрініс арқылы Мандельштам Л. И. және Андронов А. А. атсалысуымен тербелістер теориясына енгізілді. Сол уақыттан бастап бұл әдіс түрлі тербелістік құбылыстарды зерттеуде жалпыға қабылданды. Күрделі сипаттағы тербелістер, яғни динамикалық хаос пайда болған кезде оның маңызы одан да көбейді. Күрделі тербеліс процестерінің фазалық портреттер анализі хаостық шектік көбейткішінің топологиялық құрылымын жорамалдауға, сонымен қатар болашақ зерттеулерге маңызды болуы мүмкін ұсыныстар мен шынайы гипотезалар шығаруға мүмкіндік береді[10-12] .
1. 2 Хаосты сигналдар генераторлары және олардың ерекшеліктері
Қазіргі таңда хаостық сигналдарды өңдейтін динамикалық жүйелердің көптеген түрлері зерттелінген. Минималды хаостық генераторлар қарапайым үш өлшемді дифференциалды теңдеумен өрнектеледі, аз мөлшерде осы теңдеулердің бір бөлігі ретті тербелісті стандартты генераторларға бір немесе бірнеше элементтерді қосу арқылы жасалынған генераторды сипаттайды. Ал бейберекеттіліктің басқа моделін дәстүрлі электрондық генераторлармен байланыстыру оңай емес. Бірақ осы хаосты да элементтік аналогты микросхема түрінде, сандық сигналды негізде жасап шығаруға болады. Еркіндік дәрежесі 1, 5 болатын хаостың көздеріне: инерциялық бейсызықты генератор, туннельді диодты генератор, сақиналы автогенератор, Чуа тізбегі сияқты типтік үлгілер жатады. Сонымен қатар динамикалық хаосты Анищенко-Астахов генераторы белгілі, ол нақтырақ айтсақ, селективті элементтен (тербелмелі контур немесе Вин көпірі), екі күшейткіштен және инерциялық түрлендіргіші бар оң кері байланыс тізбектерінен тұратын модифицирленген бейсызық генератор [13] .
1. 2. 1 Ван-дер-Поль генераторы
Динамикалық жүйенің маңызды бөлігін тербелістер болуы мүмкін жүйелер құрайды. Тербелмелі жүйелер олардың математикалық модельдеріне қарағанда белгілі кластарға бөлінеді. Сызықты және бейсызық тербелмелі жүйелер, консервативті және диссипативті, автономды және автономды емес болып ерекшеленеді. Айтылған жүйелердің басты қасиеттері тербеліс теориясы бойынша жұмыстарда тереңінен көрсетілген [13-15] . Пуанкаре шектік циклінің динамикалық жүйе үлгісі ретінде классикалық бейсызық Ван-дер-Поль осциляторын қарастыруға болады:
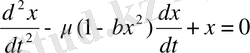 , (1. 5)
, (1. 5)
мұндағы, μ -сыртқы көзден жүйеге энергия тасуды сипаттайтын қоздыру коэффициенті (кері байланыс коэффициенті, теріс кедергі), яғни, бейсызық деңгейін сипаттайтын параметр. μ оң болған кезде жүйеде тербелістер өседі, бірақ бейсызықтықтың салдарынан олардың амплитудасы шектеледі, ал формасы синусоидаға қарағанда айтарлықтай өзгеше болады.
Ван-дер-Поль осцилляторының теңдеуін әртүрлі формада жазуға болады, ол жүйедегі параметрлер мен айнымалы динамикалық тапсырмалардың нормалауына байланысты. Әдетте Ван-дер-Поль теңдеулері мына түрде көрсетіледі:
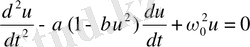 (1. 6)
(1. 6)
немесе
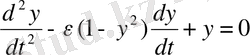 (1. 7)
(1. 7)
немесе
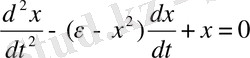 (1. 8)
(1. 8)
Бұл жерде
u, y, x
- динамикалық айнымалылар;
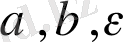 - қоздырушы автотербелмелі басқарушылар, параметрлер,
- қоздырушы автотербелмелі басқарушылар, параметрлер,
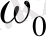 - генератордың өзіндік жиілігін сипаттаушы, коэффициент.
- генератордың өзіндік жиілігін сипаттаушы, коэффициент.
Егер (1. 6) теңдеуінен өлшемсіз уақытқа τ =
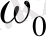 t көшсек, онда (1. 8) теңдеуді аламыз,
t көшсек, онда (1. 8) теңдеуді аламыз,
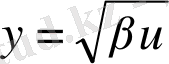 ,
,
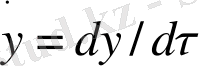 ,
,
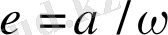 . Осындай осцилляторда өзіндік жиілік
. Осындай осцилляторда өзіндік жиілік
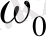 1-ге тең. (1. 8) теңдеу (1. 9) теңдеуімен мынандай алмасумен байланысты:
1-ге тең. (1. 8) теңдеу (1. 9) теңдеуімен мынандай алмасумен байланысты:
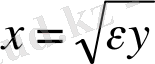 .
.
Ван дер-Поль теңдеуіне алдында айтылғандай Рэлей теңдеуі келеді:
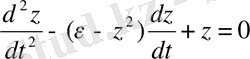 (1. 9)
(1. 9)
Егер (1. 9) теңдеуді дифференциалдап, алмастыру
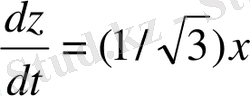 жасасақ, онда (1. 8) теңдеу шығады.
жасасақ, онда (1. 8) теңдеу шығады.
Тепе-теңдік күйі мен тұрақтылық анализі.
Автотербелістердің пайда болу шартының анықталуын білу үшін тепе-теңдік күйінің қай жүйеде бар екенін және олардың тұрақтылық сипатының басқарушы параметрлерден тәуелділігі қалай өзгеретінін білу керек. Белгілі мәліметтерді қолданып, тепе-теңдік нүктесі мен Ван - дер - Поль осцилляторының тұрақтылық сипатын негізгі теңдеуді (1. 8) алып анықтаймыз:
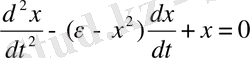 (1. 10)
(1. 10)
(1. 10) теңдеуді бірінші ретті теңдеу жүйесі түрінде қайта жазамыз:
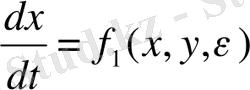
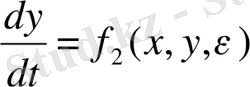 (1. 11)
(1. 11)
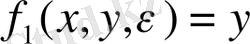
Жүйенің екі айнымалылары x және y бар, Ван дер- Поль осцилляторының фазалық кеңістігінің өлшемділігі екіге тең.
Тепе-теңдік күйі үшін теңдеудін
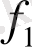 және
және
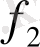 функциясын нөлге теңестіріп жазайық:
функциясын нөлге теңестіріп жазайық:
y=0,
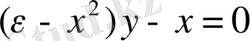 (1. 12)
(1. 12)
Координата басының фазалық жазықтығында орналасқан жалғыз ерекше нүкте бар екені көрініп тұр: х⁰=0, y⁰=0.
Тепе-теңдік күйінің тұрақтылығын анықтау үшін қозғалмайтын нүкте аймағындағы жүйені желілендіру керек және желілендіру матрицасын (немесе Якобиан матрицасын) құру керек. (1. 11), (1. 12) жүйесі үшін келесі матрицаны аламыз:
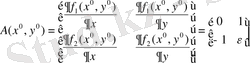 (1. 13)
(1. 13)
(1. 13) матрицаның өзіндік мағынасы Ван дер-Поль осцилляторының тепе-теңдік күйінің орнықтылығын анықтайды. Оны сипаттамалық теңдеуден оңай алуға болады:
(1. 14)
немесе
(1. 15)
Нәтижесінде екі өзіндік мағыналар шығады:
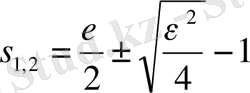 (1. 16)
(1. 16)
Ван-дер-Поль осцилляторының тепе-теңдік күйінің (х⁰=0, y⁰=0) орнықтылығын
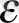 басқарушы параметрден тәуелділігін бақылайық.
басқарушы параметрден тәуелділігін бақылайық.
а)
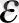 <-2 болса,
<-2 болса,
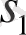 және
және
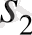 өзіндік мағыналар-шын және жалған сандар. Осындай жағдайда тепе-теңдік күйі орнықты түйінін көрсетеді.
өзіндік мағыналар-шын және жалған сандар. Осындай жағдайда тепе-теңдік күйі орнықты түйінін көрсетеді.
ә) -2<
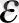 <0 болса,
<0 болса,
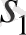 және
және
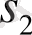 өзіндік мағыналар - комплекстік-түйіндес сандар және Re[
өзіндік мағыналар - комплекстік-түйіндес сандар және Re[
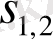 ] <0. Тепе-теңдік күйі орнықсыз фокус болады.
] <0. Тепе-теңдік күйі орнықсыз фокус болады.
б) 0<
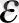 <2 болса,
<2 болса,
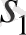 және
және
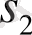 өзіндік мағыналар - комплекстік-түйіндес сандар және Re[
өзіндік мағыналар - комплекстік-түйіндес сандар және Re[
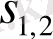 ] >0.
] >0.
в)
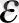 >2 болса,
>2 болса,
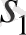 және
және
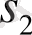 өзіндік мағыналар-шынайы оң сандар болады.
өзіндік мағыналар-шынайы оң сандар болады.
Тепе-теңдік күйі орнықсыз түйін екенін көрсетеді. Жуықталған квазигармоникалық Ван-дер-Поль теңдеуін шешетін бірнеше классикалық әдістер белгілі. Олар: энергетикалық Теодор әдісі мен Ван-дер-Поль орташалау әдісі [15, 19] .
1. 2. 2 Чуа жүйесі
Чуа тізбегі - бифуркациялық бейнелеулер мен аттракторларды бейнелейтін қарапайым электрондық схема. Тізбек 2 конденсатордан С1, С2, индуктивтік катушкадан L, сызықтық резистордан R=1/G және бейсызық элементтен NR (Чуа диоды) тұрады [27] .
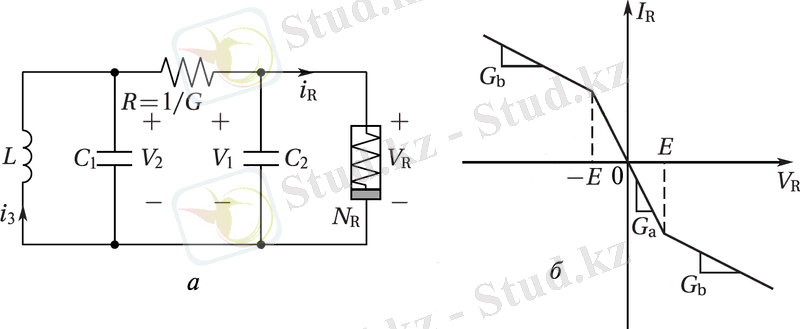
1. 1 сурет - Чуа тізбегі (а) Чуа тізбегі мен бейсызық элементінің NR вольт-амперлік сипаттамасы(б) [30]
Сурет 1. 1, б көрініп тұрғандай NR бейсызық элемент, ол әдебиеттерде Чуа диоды деп аталып, кері өткізгішпен үш құлаушы сызықтық аймағымен сипатталады: -Ga үшін VR<E және -Gb үшін VR>E.
Кері өткізгіштің бар болуы Чуа тізбегіндегі автотербелістердің мүмкіндігін қамтамасыз етеді.
1. 1, а -схемасы үшін Кирхгоф заңына сүйеніп, дифференциалдық теңдеулер жүйесін жазамыз:
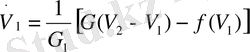 (1. 17)
(1. 17)
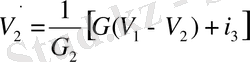 (1. 18)
(1. 18)
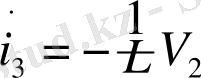
бұл жердегі, f(V1 ) функциясы бейсызық сипаттамасымен анықталады (сурет 1. 1, б) .
Келесі айнымалылар мен параметрлерді (1. 18) теңдеуіне қойсақ,
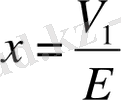
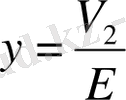
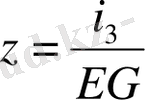
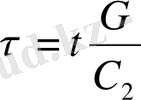
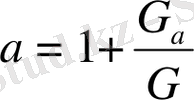
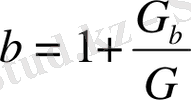
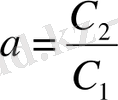
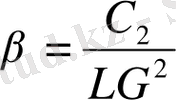
нормалау (өлшемсіз) формасындағы теңдеулер жүйесін аламыз, ол аналитикалық және сандық зерттеулер жүргізуде өте ыңғайлы болып табылады:
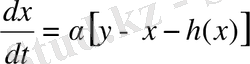
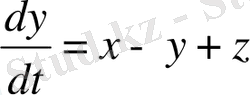 (1. 19)
(1. 19)
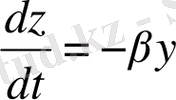
мұндағы,
 ,
,
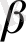 - параметрлер,
- параметрлер,
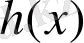 - Хевисайд функциясы,
- Хевисайд функциясы,
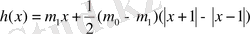 ; (1. 20)
; (1. 20)
(1. 19) теңдеуін осцилляторлық формаға у айнымалыны шығару жолымен түрлендірсек:
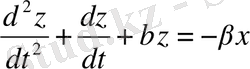
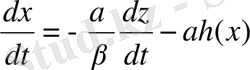 (1. 21)
(1. 21)
теңдеуінен Чуа генераторы физикалық жағынан өздігінен келісімді инерциялық қоздырғыш диссипативті осцилляторын көрсетеді.
Динамикалық жүйе (1. 21) үшөлшемді ортада R³ векторлық өрісін сипаттайды, бұл симметрияның қайта құрылуы біркелкі инвариантты:
(x, y, z) →(-x, -y, -z) (1. 22)
Жүйенің симметриясы h(x) бейсызық элементінің формалық сипаттамасымен келтірілген, ол фазалық кеңістікті үш аймаққа х=±1 жазықтықты қтармен бөле- ді:
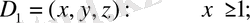
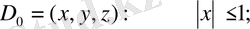 (1. 23)
(1. 23)
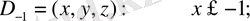
a және b параметрлері нөлден өзгеше деп шарт қойсақ қана. Әр қайсы аймақтың жүйесі
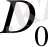 ,
,
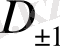 сызықты болып келеді. Осындай маңызды ерекшелікпен Чуа тізбегі аналитикалық жолмен нәтижелер қатарын ала алады.
сызықты болып келеді. Осындай маңызды ерекшелікпен Чуа тізбегі аналитикалық жолмен нәтижелер қатарын ала алады.
F жүйенің (1. 23) векторлық өрістегі дивергенциясын қарастырайық:
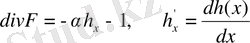 (1. 24)
(1. 24)
бұл жердегі, h'x=b үшін x∊
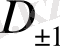 және h'x=a үшін x∊
және h'x=a үшін x∊
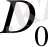 . h(x) сипаттамасы үшін келесі параметрлер мағынасын таңдаймыз: a=-0, 143, b=0, 286. (1. 23) теңдеуінен көрініп тұрғандай, а<0 шарты Ga>G білдіреді. Осы жағдайда кері өткізгіштің көзі көп болады, тізбектің активті өткізгіштігіне қарағанда b>0 шарты Gb<G және RLC-тізбегіндегі активті шығындар көп, тізбектің кіру көзіне қарағанда. Өшпейтін тербелістерді орнату үшін кері мен оң шығын арасындағы орташаландырылған баланс қажет. Демек, маңызды қорытынды жасауға болады: жүйенің (1. 23) әр фазалық траекториясы
. h(x) сипаттамасы үшін келесі параметрлер мағынасын таңдаймыз: a=-0, 143, b=0, 286. (1. 23) теңдеуінен көрініп тұрғандай, а<0 шарты Ga>G білдіреді. Осы жағдайда кері өткізгіштің көзі көп болады, тізбектің активті өткізгіштігіне қарағанда b>0 шарты Gb<G және RLC-тізбегіндегі активті шығындар көп, тізбектің кіру көзіне қарағанда. Өшпейтін тербелістерді орнату үшін кері мен оң шығын арасындағы орташаландырылған баланс қажет. Демек, маңызды қорытынды жасауға болады: жүйенің (1. 23) әр фазалық траекториясы
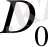 немесе
немесе
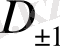 аймағында табыла алмайды. Фазалық траекториялар үш аймақтың
аймағында табыла алмайды. Фазалық траекториялар үш аймақтың
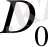 және
және
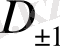 бәрін немесе екі аймаққа кіріп шыға алады:
бәрін немесе екі аймаққа кіріп шыға алады:
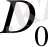 және
және
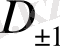 немесе
немесе
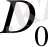 және
және
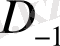 . Соңғы жағдайда симметриялық аттракторлардың үйлескен жұбы бақыланатын болады. Жоғарыда қарастырылған нәтижелер жүйенің кейбір бифуркациялық қасиеттерінің түсінігі үшін аса маңызды болады (1. 23) [17-19] .
. Соңғы жағдайда симметриялық аттракторлардың үйлескен жұбы бақыланатын болады. Жоғарыда қарастырылған нәтижелер жүйенің кейбір бифуркациялық қасиеттерінің түсінігі үшін аса маңызды болады (1. 23) [17-19] .
Чуа тізбегінде хаос белгілі аралықта болады.
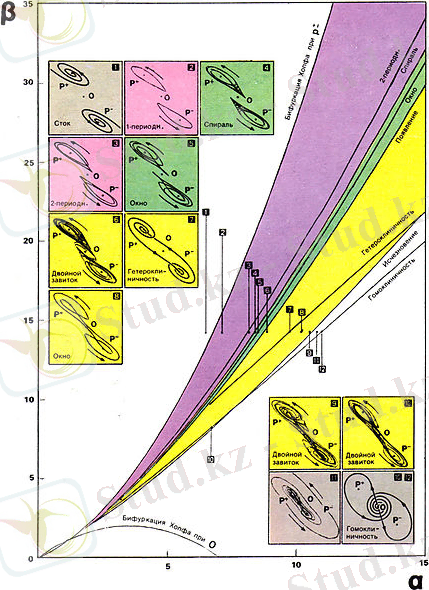
Сурет 1. 2. Чуа тізбегінің бифуркациялық диаграммасы
Осы диаграммадан есептеулерді мына аралықтарда орындаймыз:
 =[8. 5:0. 1:11] және
=[8. 5:0. 1:11] және
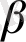 =[14. 9:0. 1:16. 5] .
=[14. 9:0. 1:16. 5] .
1. 2. 3 Анищенко-Астахов генераторы
Анищенко-Астахов генераторы - хаосты сигналдарды жүзеге асыратын бейсызықты күшейткіші бар генератор. Генератор инерциалды элементтен, күшейткіштен, конденсатордан, резистордан тұрады [14] .
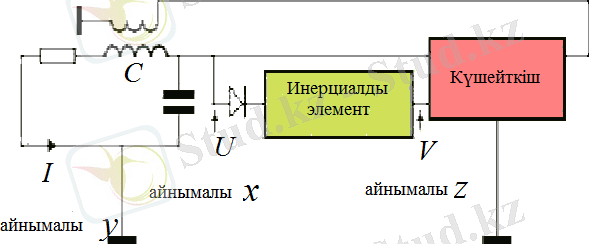
Сурет 1. 3. Анищенко-Астахов генераторының схемасы
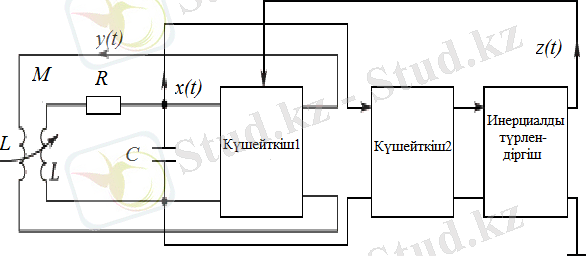
Сурет 1. 4. Инерциалды бейсызықты генератор схемасы [30]
Осы генератордың негізгі күшейткіші бейсызықты болатын болсын. Оның сипаттамасы:
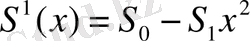 (1. 25)
(1. 25)
мұндағы,
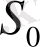 - күшейткіш сипаттамасының құламалығы. Инерциялық кері байланыстың әсерін ескерейік. Күшейткіш құламалығы:
- күшейткіш сипаттамасының құламалығы. Инерциялық кері байланыстың әсерін ескерейік. Күшейткіш құламалығы:
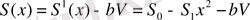 (1. 26)
(1. 26)
мұндағы, V=V(x) - инерциялық түрлендіргіштің шығысындағы кернеу, b-параметр. Инерциялық түрлендіргіш мына теңдеу арқылы жасалынатын болсын:
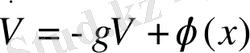 (1. 27)
(1. 27)
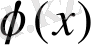 - қандайда бір бейсызық функция. Генератордың тербелмелі контурындағы ток теңдеуі:
- қандайда бір бейсызық функция. Генератордың тербелмелі контурындағы ток теңдеуі:
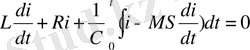 (1. 28)
(1. 28)
(1. 26) - (1. 28) теңдеулері тұйық жүйені алуға мүмкіндік береді. Ол өлшемсіз айнымалылар түрінде былай жазылады:
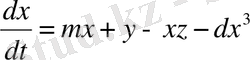 ,
,
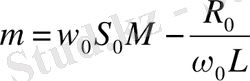
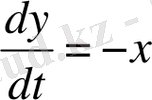 ,
,
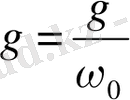 (1. 29)
(1. 29)
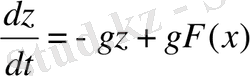
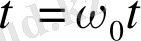
мұндағы,
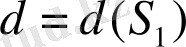 - негізгі күшейткіш сипаттамасының инерциалды бейсызықтығының әсер ету деңгейіне жауап беруші параметр, F(x) -инерциалды
- негізгі күшейткіш сипаттамасының инерциалды бейсызықтығының әсер ету деңгейіне жауап беруші параметр, F(x) -инерциалды
түрлендіргіштің бейсызықтық функциясы.
(1. 29) теңдеуден y айнымалысын ескермей теңдеу жазылса:
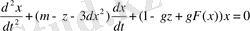
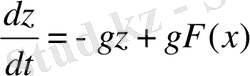 (1. 30)
(1. 30)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz