Термодинамикалық жүйелер, процестер және идеал газдардың жылу сыйымдылығы


әл-Фараби атындағы Қазақ Ұлттық университеті Биология және Биотехнология факультеті
Реферат
Тақырыбы: Негізгі термодинамикалық жүйелер
Орындаған: Сансызбаев Қасым
Қабылдаған: Құлбаева Маржан
2012 жыл
Жоспары:
- Кіріспе
- Негізгі бөлім
а. Термодинамика түсінігі
б. Көлем өзгерген кезде атқарылатын жүмыс
в. Ішкі энергия және энергияның бірдей таралу принципі
г. Идеал газдардың жылусыйымдылығының классикалық
теориясы
д. Газдың адиабаттық үлғаюы
е. Молекула-кинетикалық теорияның негіздері
ж. Химиялық термодинамика
III. Қорытынды
Термодинамикалық жүйе - бір-бірімен жэне сырткы ортамен энергия жэне зат алмаса алатын макроскопиялык денелер мен өрістердің жиынтығы
Термодинамикалық жүйенің жұмысы - термодинамикалык жүйе жағынан сыртқы денеге әсер етуші күштің жүмысы; жүйеден сырткы денеге берілген немесе одан алынған энергияға тең деп шамаланады.
Температура тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изотермиялық процесс деп атайды. Бұл процесс Бойль - Мариотт заңмен жазылады:
PV = const
Газ температурасын тұрақты ұстау үшiн, оның температурасын өзгертпейтiндей етiп жылуалмасып тұратын жүйе - термостат қажет. Әйтпесе, газ сығылғанда немесе созылғанда оның температурасының өзгерiсi елеулi. Изотермиялық процестiң ( P, V ) жазықтығындағы графигi, мзотерма деп аталатын, гиперболаны бередi
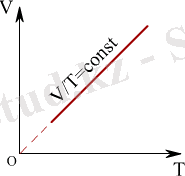
Қысым тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изобаралық процесс деп атайды. Егер ыдыста газ қысымы тұрақты болуы үшiн, оның қабырғалары жылжымалы (қозғалмалы) болуы керек. Изобаралық процестiң ( V, Т ) жазықтығындағы графигi, мзобара деп аталатын, түзу сызықты бередi (1. 11 - сурет) .
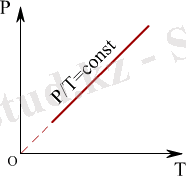
Көлем тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изохоралық процесс деп атайды. Егер газ герметикалық ыдыста болса, онда газ көлемi тұрақты болады. Изохоралық процестiң ( P, T ) жазықтығындағы графигi, мзохора деп аталатын, түзу сызықты бередi (1. 12 - сурет) .
Температуралары түрліше денелер бір-бірлерімен жанасқан кезде белгілі бір уақытган кейін олардың температураларыиың теңесетіндігін білеміз, осы кезде денелер жылулық тепе-теңдікте тұр дейді. Күнделікті өмір де, қойылған сансыз көп тәжірибелер де былай деген қорытындыға әкеледі:
Егер екі жүйе үшінші жүйемен жылулық тепе-теқдік күйде болатын болса, онда олар бір-бірлерімен жылулык тепе-теңдік күйде болады. Бүл постулатгы кейде термодинамиканьщ нөлдік бастамасы деп те атайды. Мұны бұлай атауға себеп болған термодинамиканың екі ұлы заңдары (басгамалары) аталып болғаннан кейін барып қана ғалымдардың осы постулаттаң көш басында болуы кажет екендігіне көз жеткізгендігінде болып отыр.
Сонынен, денелердің жылулық тепе-теңдіктегі куйге өтуі кезінде одардың арасында жылу (энергия) алмасу процесі өтеді.
Біз жылу дегеніміздің энергияның бір денеден екінші денеге олардың температураларының арасындағы айырымының арқасында берілу төсілі екендігіне кез жеткіздік. Бұлай қарағанда жылу жүмысқа өте ұқсас; механика бөлімінде біз жұмыстың энергияны бір денеден екінші денеге берудің механикалық төсілі екендігін көрдік. Жүмыстың бүл анықтамасын біз энергияны берудің жылудан басқа барлық түрлеріне таратамыз. Баскаша айтқанда, жүмыс дегеніміз энергияның температуралар айырымына тәуелсіз кезкелген берілу тәсілі.
Термодинамика энергияның жүмыс немесе жылу түрінде берілетін процестерімен істес болады. Біз көбіне нақты бір жүйені алып, сол жүйеге немесе сол жүйеден энергияның берілуін қарастырамыз.
Термодинамикалық жүйелердің бірнеше түрлерін қарастыруға болады. Тұйықталган жүйе-бұл массасы өзгеріссіз қалатын жүйе, Тұйық-талмағаи немесе ашық жүйе ~ бул массасы артып отыратын немесе массасы кеміп отыратын жүйе. Көп жағдайларда физикада идеалданған түйықталған жүйені қарастырады. Бірақ көптеген жүйелер ашык болады, оларға осімдіктерді, жан-жануарларды жатқызуға болады, олар сыртқы ортамен зат алмасып отырады (тамақ, оттегі жөне т. б, ) . Егер жүйенің шекаралары арқылы энергия ешбір түрде берілмейтін болса, онда жүйе туйықталган немесе оқшауланган деп, керісінше жағдайда оқшауланбаган деп аталады.
Жұмыс пен жылу күйді сипаттау үшін пайдаланылмайды. Белгілі күйдегі жүйенің белгілі жылу мөлшері немесе жұмысы болмайды. Жүйеге жұмыс атқарылған кезде (мысалы газ сығылады) немесе жүйеге жылу келІп немесе одан жылу шығарылатын болса, онда жүйенің күйі өзгереді. Сөйтіп, жүмыс пен жылу жүйені бір күйден екінші күйге еткізетін термодинамикалық процестерге кІреді екен, бірақ олар қысым, көлем, температура жөне масса тәрізді күйдІң өзінің сипаттамалары бола алмайды.
Көлем өзгерген кезде атқарылатын жүмыс
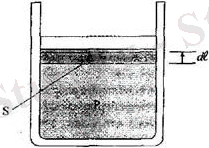 Енді жүмысты ең қарапайым жөне ең көп кездесетін термодинамикалық процесс - көлемнің өзгеруі, мысалға, газдың үлғаюы немесе сығылуы кезінде атқарылатын жүмысты есептеуден бастайық. Газдың қайсы-бір мөлшері жылжымалы поршенмен жабылған ци-линдр түріндегі ыдыстың ішінде болсын делік Әрқашан ең алдымен қарастырылып отырған системамыздың не екендігіне қатты назар аударуымыз керек. Біздің жағдайымызда система ретінде газды алып отырмыз: демек, ыдыстың қабырғасы жөне поршен қор-шаған ортаға жатады. Енді газдың
квазистатикалыц
(статикалық «дерлік») үлғаюы кезінде атқарылатын жүмысты есептеп шығарайық. Квазистатика-лық деп біз өте баяу отетін процесті - идеал жағдайда шексІз аз жылдамдық-пен өтетІн процесті түсінемІз; бүл - система шексіз жақын орналаскан тепе-тенді күйлер тізбегін өтсді дегенді білдіреді. Осы кезде системаның
р
қысы-мы мен
Т
температурасын кезкелген мезетте анықтауға болады. Поршеннің астындағы газ үлғаиып күш түсіреді, мүндағы
р -
газ
Енді жүмысты ең қарапайым жөне ең көп кездесетін термодинамикалық процесс - көлемнің өзгеруі, мысалға, газдың үлғаюы немесе сығылуы кезінде атқарылатын жүмысты есептеуден бастайық. Газдың қайсы-бір мөлшері жылжымалы поршенмен жабылған ци-линдр түріндегі ыдыстың ішінде болсын делік Әрқашан ең алдымен қарастырылып отырған системамыздың не екендігіне қатты назар аударуымыз керек. Біздің жағдайымызда система ретінде газды алып отырмыз: демек, ыдыстың қабырғасы жөне поршен қор-шаған ортаға жатады. Енді газдың
квазистатикалыц
(статикалық «дерлік») үлғаюы кезінде атқарылатын жүмысты есептеп шығарайық. Квазистатика-лық деп біз өте баяу отетін процесті - идеал жағдайда шексІз аз жылдамдық-пен өтетІн процесті түсінемІз; бүл - система шексіз жақын орналаскан тепе-тенді күйлер тізбегін өтсді дегенді білдіреді. Осы кезде системаның
р
қысы-мы мен
Т
температурасын кезкелген мезетте анықтауға болады. Поршеннің астындағы газ үлғаиып күш түсіреді, мүндағы
р -
газ
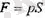 , поршенге дың қысымы, ал 5 поршенңщ ауданы. Газдың поршенді шексіз аз
қашықтыққа жылжытқан кезде атқаратын жүмысы мынандай өрнекпен берІледі:
, поршенге дың қысымы, ал 5 поршенңщ ауданы. Газдың поршенді шексіз аз
қашықтыққа жылжытқан кезде атқаратын жүмысы мынандай өрнекпен берІледі:
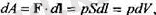 (2. 1. )
(2. 1. )
екендігін ескердік. біз бүл жерде көлемнің шексІз аз үлғаюының
Егер газ сығылған болса, онда сіі векторы газы бар ыдыстың ішіне қарай бағытталып, көлем азайған болар еді, яғни ^у < 0 болар еді. Бүл жағдайда поршеңді орын жылжыту бойынша атқарылған жүмыс теріс болып, бүл дегеніміз газга
оң жүмыс аткарылады дегенді білдірген болар еді. Көлемнің Ғ, мәннен
у
г
мәнге дейінгі аральтқта шекті озгерІсі кезінде газдың аткдрған жүмысы;
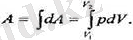 (2. 2)
(2. 2)
(2. 1) және (2. 2) өрнектер колемнің кезкелген өзгерістері кезінде, егер бүл озгерістер квазистатикалык болатын болса, газдың сүйықтың немесе қатты дененің атқаратын жүмысын сипаттайды. (2. 2) өрнектІ интегралдау үшін про-цесс кезінде қысымның қалай езге-ретіндігін білу керек, ал бүл процестің түріне тәуелді болады. Бізге идеал газдың белгілі мөлшерІ беріліп, оның көлемін V, -ден
У
2
-ге
дейін бастапқы және ақырғы температура бірдей болатындай етіп, яғни
Т
{
= Т
2
болатындай үлғайту керек болсын Мүны іске асыру үшін газға квази-статикалық түрде түрақты температура кезінде үлғаюға мүмкіндік беруіміз қажет. Мүндай процесс
изотермиялық
деп аталады. Бүл процесті
рУ
диаграммадағы I және 2 нүктелер арасындағы қисық түрінде өрнектеуге болады. Осы процесс кезінде атқарылатын жүмыс, (2. 2) өрнекке сай,
рУ
диаграммадағы процесс қисығы мен
V
осінің арасындағы ауданға тең болады. (2. 2) өрнектің оң жағындағы интегралды идеал газ үшін оның күйінің
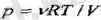 (2. 3)
(2. 3)
өрнегін пайдалана отырып есептеп шығаруға болады. Сонда атқарылған А жұмыс мына түрде жазылады
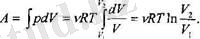
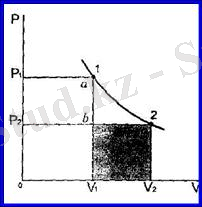
Енді I күйден 2 күйге өткізудің басқа жолын қарастырайық . Бүл үшін өуелі газдың көлемін өзгертпей, оның қысымын Р, -ден Р
2
-ге дейін төмендетіп содан кейін газғатүрақты
р
2
қысым кезінде V келемнен
V2
көлемге дейін ұлғаюға мүмкіндік береміз . Бірінші
аЬ
учаскеде газ жүмыс атқармайды, себебі колем өзгеріссіз қалады:
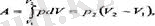
сөйлп, газдың аткарған жүмысы тағы да
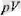 диаграммада
аһс
процесс қисығы мен
V
өсімен шектелген ауданға тең болады. Идеал газдын, кұй теңдеуін пайда-ланып, мынандай ернекке де келуге болады
диаграммада
аһс
процесс қисығы мен
V
өсімен шектелген ауданға тең болады. Идеал газдын, кұй теңдеуін пайда-ланып, мынандай ернекке де келуге болады
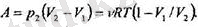 (2. 4)
(2. 4)
Осы алынған нәтижелерді салыстыра отырып, мынандай қорытындыға келеміз: система бір күйден екіншІ күйге еткен кезде атқарылатын жүмыс тек бастапқы және ақырғы күйлерге ғана емес, сонымен қатар процестің түріне де (немесе жүріп өтілген "жолдың" түріне де) тәуелді болады.
Бүл- жүмысты системанын, озше ғана тән қасиет деп қарастыруға болмай-тындығын тағы да дәлелдейді. Жылу жайлы да дөл осыны айтуға болады:
Система бір күйден екінші күйге өткен кезде алынатын немесе бері-летін жылу тек бастапқы жэне ақырғы күйлерге ғана емес, сонымен қатар процестің түріне де (немесе жүріп өтілген "жолдың" түріне де) тәуелді болады.
Ішкі энергия және энергияның бірдей таралу принципі
Идеал газдың ішкі энергиясы тек қана температураға тәуелді болады:
V = bТ, (2. 6)
мүндағы Ь- пропорционалдық коэффициентІ, ол температураның біршама кең интервалында тұрақты болып қалады.
Ішкі энергияда газдың алатын көлеміне төуелділіктің жоқтығы идеал газ нолекулаларының басым уақытын бір-бірімен озара өрекеттеспей өткізе-тіндігін көрсетеді.
Денснің температурасын бір кельвинге арттыру үшін оған берілетін жылу мөлшеріне тсң шама дененің жылу сыйымдылығы деп аталады.
Егер денеге берілген жылу молшері оның гемпературасын ΔТ шамасына ар ттыратын болса, онда анықтама бойынша, жылу сыйымдылық
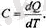 (2. 7)
(2. 7)
Бұл шама кельвинге бөлінген джоулдермен өлшенеді (Дж/К)
Молдік жылусиымдылық деп аталатын заттың молінің жылу сыйым-дылығын біз үлкен С өрпімен белгілейтін боламыз: С (Дж/мопъ. К)
Заттың бірлік массасының жылу сыйымдылығы меишікті жылу сыйым-дылық деп аталады. Оны кішкентай с өрпімен белгілейміз және оиың өлшем бірлігі ІДж/кг. К)
Бір ғана заттың молдік және меншікті жылу сыйымдылықтарының ара-сында мынандай қатынас бар:
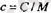 (2. 8)
(2. 8)
(М~ молдік масса) .
Жылу сыйымдылықтың мөлшері дененің қандай жағдайларда қьгздыры-лғанына тәуелді.
Тұрақты көлем кезіндегі жылу сыйымдылық (
С
у
) . Егер дене түрақты көлем кезінде қыздырылатын болса, дене сырт денелерге қатысты жүмыс атқармайды жөне
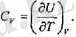 (2. 9)
(2. 9)
болады. Осыдан
Мүндайжазу V дегенді білдіреді. Идеал газ жағдайында V тек Т температураға ғана төуелді болатындықтан, (2. 9) ернекті төмендегіше жазуға болады:
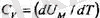
(молдік жылу сыйымдылықты алу үшін газдың бір молінің ішкі энергиясын алу керек) .
Газдардын, жылу сыйымдылығы қатгы денелер мен сүйықтарға қараған-да газдьің қандай процеске қатысатьшдығына күштірек тәуелді болады. Газ-дар үшін аса маңызды екі процесс бар, олар - көлем немесе қысьш түрақты болып қалатын процесс.
Газдар үшін С, - молдік жылу сыйымдылықпен катар С р жылу сыйым-
дылықты да енгізу керек. Сонда газдың у молін Д7* кельвинге қыздыруға қажетті жылу мөлшері былай жазылады:
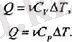
Мүндағы молдік жылу сыйымдылықтар мен меншікті жылу сыйымды-лыктар арасындағы байланыс мынандай:
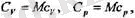
7 М - газдың молдік массасы.
Енді молекулалық-кинетикалық теорияны паидалана отырып, неліктен газдардың түрақты кысым кезінде өтетін процестері үшін жылу сыйымды-Аіқтың түрақты колем кезінде өтетін процестер кезіндегі жылу сыйымды-яықтан артық болатындығын анықтайық. Идеал газды өуелі гүрақты келем кезінде, сосын түрақты кьісым кезінде баяу қыздырылады деп алайық. Екі
ироцесс кезінде де температура бірдей АТ шамасына өзгеретін болсын делік. Түрақты көлем кезінде өтетін процесс кезінде ешкандай жүмыс атқарылмайды, себеб
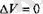
болады. Сонымен, термодинамиканың бірінші бастамаҖына сай, системаға берілетін
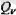 жылу мөлшері гүгелінен системаның ішкі энергиясын өзгертуге кетеді екен:
жылу мөлшері гүгелінен системаның ішкі энергиясын өзгертуге кетеді екен:
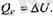
Түрақты қысымда ететін процесс кезінде система жүмыс та атқарады, язондықтан системаға берілген б
р
жылу молшері тек қана системаның ішкі эңергиясын езгертуте ғана емес, сонымен катар
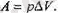 жүмыс атқаруға да шығындалады: Демек, бүл процесс кезінде бірінші процеске карағанда
жүмыс атқаруға да шығындалады: Демек, бүл процесс кезінде бірінші процеске карағанда
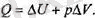
Екі процесс кезінде де ішкі энергияның өзгерісі бірдей болатындықтан
(екі жағдайда да ДГ бірдей) системаға жылуды кобірек беру керек, сонда термодинамиканың біршші ба-^№амасы бойынша:
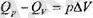
болады. Идеал газ үшін
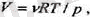
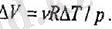
сондықтан түрақты қысым кезінде өтетін процесс үшін
. Осы өрнекті жоғарыдағы қатынасқа қойып, әрі (11. 6) қатынасты пайдалансақ, онда мынаған келеміз.
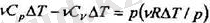
және
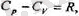 немесе
немесе
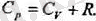 (2. 13. )
(2. 13. )
Сонымен, идеал газдың бір молінің температурасын түрақты қысым кезінде бір келышнге көтерген кезде атқаратын жүмысы Я газ түрақтысына тең болады екен. Бүл қатынас тек идеал газ үшін ғана орындалады.
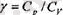 (2. 14. )
(2. 14. )
шамасы өрбір газ үшін белгілі мәні бар шама болып табылады. Бір атомдық газ үшш ол 5/3, екі атомдық газ үшін 7/5, ал уш атомдық газ үшін 4/3 жөне т. б. жөне газдың адиабаттыц көрсеткіші деп аталады. (2. 14) бойынша
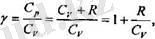
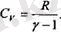
осыдан
Осы С у (11. 11) өрнегіне қойып,
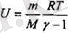
деп жазуға болады. Егер Клапейрон-Менделеев теңдеуін пайдалансақ, онда ішкі энергияның тағы бір орнегін аламыз:
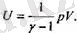
ЕндІ газдардың молекулалық-кинетикалық теориясын пайдаланып,
бір
атомдық газдың молдік жылу сыйымдылығын есептеп шығарайық. Әуелі түрақты көлем кезінде отетін процесті қарастырайық. Бүл кезде термодина-миканың бірінші бастамасы бойынша жүмыс атқарылмайтын болғандықтан, егер газға Җ) жылу мөлшері бегілген болса, онда оның ішкі энергиясы
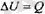
шамасына өзгереді. Бір атомдық идеал газдың II ішкі энергиясы барлық молекулалардың толық кинетикалық энергиясына тең болады жөне жоғары-да көрсеткендей, ол:
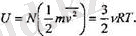
Енді (2. 6а) қатынасты пайдаланатын болсақ, онда былай деп жазуға болады:
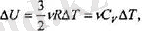
осыдан
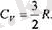
Табылған мән тожірибе нөтижесіне өте жуык-
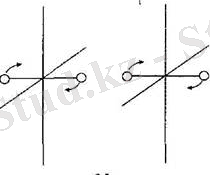 Екі атомдық (молекуласы екі атом-нан түрады) және үш атомдық (моле-куласы үш атомнан түрады) төрізді күрделірек газдардың өлшенілген жылу сыйымдылықтары молекуладағы атомдар саны артқан сайын артып оты-рады екен. Мүның себебі - ішкі энер-гия тек ілгермелі қозғалыстың кинети-калық энергиясынан ғана емес, соны-мен қатар энергияның басқа түрлері-нен де түратындығы. Мысалға екі атомдық газды алайық. 2. 5-суретте корсетілгендей, екі атом түрліше екі
Екі атомдық (молекуласы екі атом-нан түрады) және үш атомдық (моле-куласы үш атомнан түрады) төрізді күрделірек газдардың өлшенілген жылу сыйымдылықтары молекуладағы атомдар саны артқан сайын артып оты-рады екен. Мүның себебі - ішкі энер-гия тек ілгермелі қозғалыстың кинети-калық энергиясынан ғана емес, соны-мен қатар энергияның басқа түрлері-нен де түратындығы. Мысалға екі атомдық газды алайық. 2. 5-суретте корсетілгендей, екі атом түрліше екі
өске қатысты аЙнала алады (екі атом арқылы да өтетш оске қатысты айналыс энергияға онша үлес қоса алмайды, себебі молекуланың осы өске қатысты анықталған инерция моменті мардымсыз аз) . Сонымен, молекуланың Ілгері-лемелі қозғалыс кинетикалық энергиясымен қатар айналмалы қозғалыс ки-нетикалық энергиясы да болады. Бүл жағдайда еркіндік дәрежелері түсінігін енгізген қолайлы. Біздің жағдайымызда
еркіндік дәрежелері саны деп малекулаларга энергия берудің тәуелсіз тәсілдерініц санын түсінетін боламыз.
Мысалы, бір атомдық газдың үш еркіндік дөрежелері бар дейді, себебі атом
X, у
жәнс
Z,
өстері бойымен бағытталған -ды: осы остер бойымен қозғалыстар өзара тәуелсІз болып саналады, себебі олардың кез келгенінің қозғалыс параметрі басқаларына тәуелсіз болады. Екі атомдық молекуланың да бір атомдық молеқула тәрізді, ілгерілемелі козға-лыс кинетикалық энергиясымен байланысты болатын үш еркіндік дөреже-лері болады және сонымен қатар, айналмалы қозғалыс кинетикалык энерги-ясымен байланысты болатын тағы екі атомдық дөрежелері болады: сонда бар-лығы бес еркіндік дөрежесі шығады. Төжірибе көрсеткендей, екі атомдық газдың
Су
жылу сыйымдылғы бір атомдық газдың жылу сыйымдылығының 5/3 бөлігіндёй болады, яғни жылу сыйымдылықтар қатынасы еркіндік дорежелері сандары қатынасындай болады екен. Осы дерек он тоғызыншы ғасыр физиктерін аса маңызды энергияның бірдей таралу принципі деген принципке жетектеді. Бұл принцип бойынша, энергия молекуланың еркіндік дәрежелері арасында бірдей таралады және әрбір еркіндік дәрежесіне ор аша есеппен
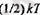 энергия келеді. Сонда. біратомдык газдын молекүласының орташа энергиясы
энергия келеді. Сонда. біратомдык газдын молекүласының орташа энергиясы
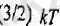 болу керек те, ал екі атомдық газ молекуласы үшін
болу керек те, ал екі атомдық газ молекуласы үшін
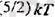 болу керек. Демек, екі атомдық газдың ішкі энергиясы
болу керек. Демек, екі атомдық газдың ішкі энергиясы
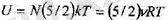 болады, мұндағы у-молдер саны. Осы айтылғандарға сүйеніп жылусыйымдылықтарға қатысты барлық шамаларды есептеп шығаруға болатын секілді еді. Бірақ, теменгі температуралар кезіңде екі атомдық газдың
болады, мұндағы у-молдер саны. Осы айтылғандарға сүйеніп жылусыйымдылықтарға қатысты барлық шамаларды есептеп шығаруға болатын секілді еді. Бірақ, теменгі температуралар кезіңде екі атомдық газдың
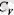 жылу сыйымдылығы бар болғаны
жылу сыйымдылығы бар болғаны
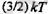 болып шықты, яғни молекуланың тек үш қана еркіндік дөрежелері бар секідді. Ал өте жоғары температуралар кезінде жылу сиымдылық шамамен(7/2) болып шықты, яғни газдың жеті еркіндік дәрежелері бар секілді. Бүлардың барлығы былайша түсіндіріледі:
өте төмен температуралар кезінде молекуланыц иегізінен тек ілгермелі цозгалыстың кинетикапық энергиясы гана болады;
басқаша айтқанда, айнымалы қозғалысқа энергия жұмсалмайды, тек үш еркіндік дәрежесі ғана жүмыста болады. Ал аса жоғары температуралар кез-інде барлық бес еркіндік дорежелері де іске қосылады және қосымша екі еркіндік дәрежелері пайда болады. Осы қосымша екі еркіңдік дөрежелерін
болып шықты, яғни молекуланың тек үш қана еркіндік дөрежелері бар секідді. Ал өте жоғары температуралар кезінде жылу сиымдылық шамамен(7/2) болып шықты, яғни газдың жеті еркіндік дәрежелері бар секілді. Бүлардың барлығы былайша түсіндіріледі:
өте төмен температуралар кезінде молекуланыц иегізінен тек ілгермелі цозгалыстың кинетикапық энергиясы гана болады;
басқаша айтқанда, айнымалы қозғалысқа энергия жұмсалмайды, тек үш еркіндік дәрежесі ғана жүмыста болады. Ал аса жоғары температуралар кез-інде барлық бес еркіндік дорежелері де іске қосылады және қосымша екі еркіндік дәрежелері пайда болады. Осы қосымша екі еркіңдік дөрежелерін
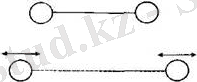 түсіндіругеболады, яғни серіппемен жалғасқан атомдардьщ тербелістері түрінде түсІңдіруге болады . Бір еркіңдік дэрежесі тербелмелі қозғалыстан кинетикалық энергиясынан ту са, екінші еркіндікк дәрежесі - тербелмелі қозғалыстың потенциалдық энергиясынан
түсіндіругеболады, яғни серіппемен жалғасқан атомдардьщ тербелістері түрінде түсІңдіруге болады . Бір еркіңдік дэрежесі тербелмелі қозғалыстан кинетикалық энергиясынан ту са, екінші еркіндікк дәрежесі - тербелмелі қозғалыстың потенциалдық энергиясынан
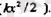
Идеал газдардың жылусыйымдылығының классикалық теориясы
1. Жылу сыйымдылықтың классикалық теориясы атом-молекулалық жүйелерге классикалыц ньютон мехаиикасының заңдарын қолдануға болады деген тоқтамға суйенеді. Шын мөнісінде ньютондык, механиканын. атом-молекулалык жүйелерге қолданылуы шектеулі. Осы себептен де классикалық теория жылу сыйымдылық мәселелерін толық қанағаттанарлықтай шеше алмады да, оны жалпыламырақ кванттық теориямен алмастыруға тура келді. Бірақ та кептеген жағдайларда классикалық теория тәжірибемен үйлесімділікке алып келеді. Мүның себебі калссикалық теория дегеніміз кванттық теорияның шектік жуықталуы болып табылады, сондықтан оиың күші жететін белгілі өз аумағы бар. Мүндай жағдайларда классикалық теорияның қорытындыларының кванттық теория қорытындыларынан еш айырмашылығы жоқ деуге болады. Сондықтан классикалық теорияға тоқталамыз, ол кванттық теорияға қарағанда қарапайым. Осы арқылы классикалық теория Бұның қиындықтарын анығырақ көріп, олардың шешімін кванттық теорияның қалай беретінін жеңіл қабылдай аламыз.
Классикалық жүйелер үшін кинетикалық энергияның еркіндік дәрежелері бойынша тең таралуы теоремесы орындалады. Осы теорияның негізінде газ-дар мен қатты денелердІң жылусыйымдылығының классикалық теориясын түзуге болады. Газдардьтң жылу сыйымдылығынан бастаймыз. Жоғарыда идеал газдар үшін
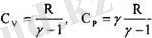
болатындығын керсеткенбіз. Осыдан керіп отырғанымыздай, у адиабатгық түрақты идеал газдың екі С р жөне С у жылусыйымдылықтарын да бірмәнділікпен анықтайды . Сондықтан теорияны төжірибемен салыстыру үшін тек / адиабаттық түрақтының ғана тәжірибелік және теориялық мәндерін озара салыстырсақ жеткілікті .
Газдың ішкі энергиясы молекулалар мен атомдардың шгерілемелі, айнал-малы және ішкі қозғалыстарының кинетикалық энергиясынан және олардың өзара әрекеттесуінің түрады. Молекулалық күштер ескерімсіз аз болатын идеал газдар үшін молекулалардың өзара әрекетгесу потенциалдық энергиясын ескермеуге болады.
Бірагпамдық газдардың жылусыйымдылыгы.
Біратомдық газдың моле-кулаларын материалдық нүктелер деп қарастыратын боламыз. Олар тек ілгер-мелі қозғалыстар ғана жасай алады. Газдың ішкі энергиясы дегеніміз атом-дардың ілгермелі қозғалысының кинетикалық энергиясына айналады. Бір ато-
мға шаққандағы орташа кинетикалық энергия болады. Газдың бір молІнІң ішкі энергиясы үшін сонда:
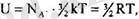
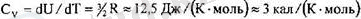
мүндағы Ы А - Авогадро саны. Осыдан тұрақты көлем кезіндегі молдік жы-лусыйымдылықты табамыз:
және түрақты қысым кезінде
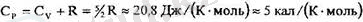
Адиабата корстекіші
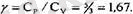
Бір атомдық газдар үшін тәжірибелік мәндері 1-кестеде келтІрілген. Төжірибемен үйлесімділік өте жақсы. тығы өзгеріссіз қалады дегенді білдіреді. Сонымен, тәуелсіз коорди-наттар саны бес болып шығады. Сөйтіп, біздің екі атомдық молекула-ның моделінің бес еркіндік дәрежесі болады екен.
Классикалық теория молекуланың конфигурациясын анықтайтын нақты координаттарды білуді қажет етпейді. Молекуланың түтастай алғандағы орташа
н§
Не
Ке Аг
527 Г290
\93
292 [288
[98
1, 666
1, 660 1, 673 1, 64
1, 65 1, 69
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz