Күрделі аттракторлы хаос генераторлары: модельдер мен радиобайланыстағы қолданылуы


КІРІСПЕ
Хаостық тербелістер - жақын арада ғана бейсызық динамикалық жүйелерде анықталған құбылыс. Мұндай қозғалыстар бұрынғы уақытта да бақыланған, алайда ол жақында ғана электрлік бейсызық жүйелерде анықталды. Хаостық тербелістердің төменгі ретті бейсызық детерминді жүйелерде пайда болу мүмкіндігі анықталды және ретсіз шуылдың пайда болу көзін түсінуге және оны басқара алу мүмкіндігінің үміті пайда болды. Хаос генераторлары - спектралды, статистикалық және басқа да қасиеттері бар хаостық тербелістерді беретін құрылғы. Қазіргі уақытта динамикалық хаос негізіндегі информациялық технологияларды ақпаратты жіберу, өңдеу, сақтау және қорғау үшін қолданылады. Динамикалық хаос - күрделі, периодсыз қозғалыс. Бұл қозғалыс сыртқы шуыл жоқ кезде пайда болуы мүмкін және толығымен детерминді динамикалық жүйенін өзінің қасиеттерімен анықталады. Сонымен қатар ол бейсызық жүйенің тәртібі. Автотербелмелі жүйелер диссипативті тербелмелі контурдан, контурдағы энергия шығынының орнын қалпына келтіріп тұратын қорек көзінен және қалпына келтірілген тербелісті кері байланыс тізбегінде реттейтін бейсызық құрылғыдан құралады. Автотербелмелі жүйеде егер бір период ішіндегі энергия шығыны аз болса, ал контурға периодты түрде түсіп тұратын энергия шығындарды өтеп, энергетикалық балансты қайта қалпына келтіретін болса, онда автотербелістердің формасы синусоидалы тербелістерге жақын болады (томсон типтес автогенерторлар) . Ал егерде, тербелмелі жүйедегі энергия период барысында толығымен шығындалса және оның орнын толтыру әр период сайын үлкен мөлшерлермен орындалса, онда тербелістердің формасы синусоидалыдан әлдеқайда ерекше болады. Яғни, кез-келген қарапайым автотербелмелі жүйе бейсызық элеметтен тұрады. Жүйеде пайда болатын автотербелістер бейсызық диссипативті жүйедегі сөнбейтін тербелістер. Бұл тербелістер уақыт өте келе фазалық траекторияда өзіне тартатын көптеген нүктелердің жиынтығына айналады, ол аттрактор деп аталады.
Қазіргі таңда аса жоғары жиілікті (АЖЖ) және кеңжолақты диапазондағы хаос генераторларын зерттеу өзекті тақырыптардың бірі болып табылады, солардың біріне күрделі аттракторлы хаос генераторлары жатады. Генератордың мұндай түрін қаныққын бейсызық функцияға негізделе отырып аламыз. Бұл жұмыста ұсынылып отырылған бейсызық элемент сатылы және көп сатылы (ступенчатый) қаныққан бейсызық функциямен сипатталады.
1. ХАОСТЫҚ ГЕНЕРАТОРЛАР ЖӘНЕ ОЛАРДЫҢ ҚОЛДАНЫС АЯСЫ
1. 1. Динамикалық хаос құбылысы
«Хаос» сөзі гректің «χαοζ» сөзінен тараған. Бастапқыда бұл сөз барлық басқа заттар пайда болғанға дейінгі шексіз кеңістік деген мағынаны білдірген. Кейін римдіктер хаос сөзінің түпнұсқасын дымқыл пішінсіз масса деп аударған және оған Жаратушы үйлесім мен реттілік берді деген. Қазіргі біздің қолданысымыздағы заманауи түсінік бойынша хаос дегеніміз ретсіз және тұрақсыз күй деген мағынаны білдіреді. Хаос теориясы-жеткілікті жас математикалық аймақ болып табылады. Хаос бейсызық динамикалық жүйелерде пайда болады.
Бейсызық жүйелерде ретсіз (хаосты) қозғалыстардың пайда болу аналогиясы бойынша динамикалық немесе детерминді хаос термині пайда болды. Хаостық тәртіп сыртқы шуыл көздерінен, еркіндік дәрежесінің үлкен санынан және кванттық механикамен байланысты анықталмағандықтан пайда болмайды, ол бейсызық детерминді жүйенің меншікті динамикасынан пайда болады. Фазалық кеңістікте мұндай тәртіп жүйесіне әуейі аттрактор сәйкес келеді.
Хаостық тербелістер - жақын арада ғана бейсызық динамикалық жүйелерде анықталған құбылыс. Мұндай қозғалыстар бұрынғы уақытта да гидродинамика саласында бақыланған, алайда ол жақында ғана электрлік бейсызық жүйелерде анықталды. Хаостық тербелістердің төменгі ретті бейсызық детерминді жүйелерде пайда болу мүмкіндігі анықталды және ретсіз шуылдың пайда болу көзін түсінуге және оны басқара алу мүмкіндігінің үміті пайда болды. Бейсызық динамиканың жаңалықтары физикалық жүйелерде хаостық тербелістердің жаңа идеяларының және регистрация әдістерінің пайда болуына алып келді және «детерминді шуылға» фракталды өлшем және Ляпунов көрсеткіші секілді өлшемдердің көмегімен сапалы анализ жасауға жаңа идеялар тудырды. Хаос теориясына ең үлкен үлесін метеоролог Эдвард Лоренц қосты [1] .
Динамикалық (детерминді) хаос - күрделі, периодсыз қозғалыс. Бұл қозғалыс сыртқы шуыл жоқ кезде пайда болуы мүмкін және толығымен детерминді динамикалық жүйенің өзінің қасиеттерімен анықталады. Динамикалық хаос кездейсоқ процесстердің көптеген қасиеттеріне ие (қуаттың тұтас спектрі, бәсеңдеуші корреляциялық функция) .
Сонымен қатар, динамикалық хаос - бейсызық жүйенің тәртібі ол детерминді заңдармен анықталатынына қарамастан бейсызық жүйе кездейсоқ болып көрінетін динамикалық жүйе теориясындағы құбылыс .
Хаостың пайда болу себебі бастапқы шарттарға және параметрлерге қатысты тұрақсыздық (сезімталдық) болып табылады: уақыт өте келе, бастапқы шарттың сәл де болсын өзгерісі жүйенің динамикасының үлкен өзгерістеріне алып келеді (траекторияның уақыт бойынша экспоненциалды таралуы, Ляпунов көрсеткіші) .
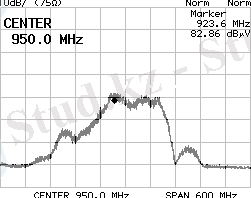
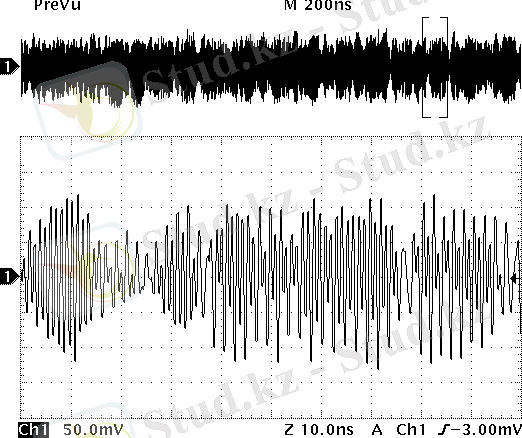
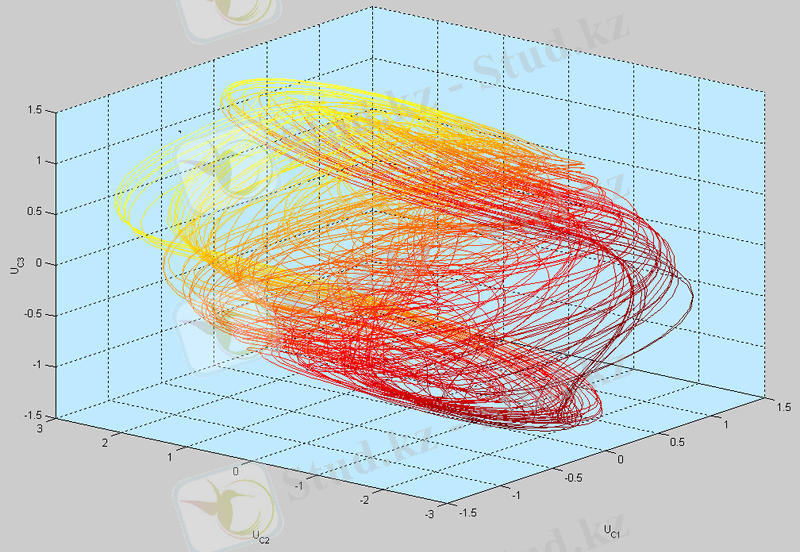


Детерминді (динамикалық) хаос режиміндегі жүйенің күй координаттарының уақыт бойынша тәуелділігі күрделі функциямен сипатталады. Оның қасиеттерін анықтау жаңа сандық сипаттамаларды енгізуді талап етеді, ол периодты немесе квазипериодты режим сипаттамаларынан ерекшеленуі керек [2] .
«Детерминді хаос» бүгінгі күндері көптеген үздік нәтижелер алынған зерттеудің активті аймағы болып табылады. Хаостың әртүрлі типтерінің классификация әдістері жасалынды және сыртқы басқарушы параметрді өзгерткен кезде көпшілік жүйелер тәртіптен хаосқа жақын ауысуларды көрсетті. Детерминді қозғалыс жеткілікті тұрақты және хаостық қозғалысқа жақын емес болады, себебі тізбектей жағдайында біреуі басқасынан үздіксіз дамиды. Алайда, біздің ғасырдың шегінде және өткен ғасырда математик А. Пуанкаре уақыт бойынша Гамильтон теңдеулерімен анықталатын кейбір механикалық жүйелерде хаостық қозғалыс болу мүмкін екендігін анықтаған. Өкінішке орай, метеоролог Е. Н. Лоренц тіпті бірінші ретті байланысқан үш дифференциалдық теңдеулерден жасалған қарапайым дифференциалдық жүйе хаостық траектория алып келетінін ашпайынша, көпшілік физиктердің тарапынан бұл әзіл ретінде қабылданды. Бүгінгі күні көпшіліктің растауына ие болған Лоренцтің жұмысы бірнеше жылдар бойы жарияланғаннан кейін де атағы аздау болып қала берді. Ол диссипативті жүйелердегі детерминді хаостың ең алғашқы мысалдарының бірін келтірді. Детерминді хаос сөзі бейсызық жүйелерден туындайтын тұрақсыз немесе хаостық қозғалыс дегенді білдіреді. Детерминді бейсызық диссипативті жүйелердегі хаостық процесстер - зерттеушілердің назарындағы заманауи жаратылыстану пәнінін фундаментті проблемаларының бірі болып табылады. Мұндай жүйелерде физикалық сипаттамалары бойынша шынайы кездейсоқ тербелістерден ерекшелене алмайтын күрделі тербелісті процесстердің генерациясы үлкен еркіндік дәреже санымен және флуктуацияның болуында емес, экспоненциалды тұрақсыздық режимдерінде болады. Қазіргі уақытта А. Пуанкаре идеясының дамуы детерминді жүйелердің хаостық динамикасының фундаментін жасауға алып келді. Дифференциалды жүйелердегі хаостың пайда болуының қажетті шарты N 3 болып табылады, бұл фазалық кеңістіктің өлшемділігі және сөнбейтін хаостық пульсациялардың туындауы еркіндік дәрежесі 1, 5-ке тең генераторларда мүмкін болады. Детерминизм толық бірмәнді болжаумен және қайта қалпына келумен, ал хаос толық болжаудың жоқтығымен және қайта қалпына келе алмауымен байланысты. Егер біз үш тәуелсіз айнымалымен сипатталатын (фазалық координаталар) динамикалық жүйені қарастырсақ, онда жағдай түбегейлі түрде өзгеруі мүмкін. Кеңістікте үш өлшемді жүзеге асыру үшін бізге ештеме кедергі болмайды. Траектория нүктеден спираль бойынша алыстап, үшөлшемді кеңістікке айналады. Кейбір мәндерге қол жеткізіп және бейсызық шектеудің қозғалыс механизмін көре отырып, траектория қайтадан бастапқы қалпының маңайына қайтып келеді. Ары қарай, тұрақсыздықдың әсерінен процесс қайталанып отырады. Осы кезде екі түрлі жағдай орын алуы мүмкін: траектория уақыт өткеннен кейін кейбір күрделі бірақ периодты процесті көрсете отырып тұйықталады; траектория, егер t кезінде тұйықтаулар болмаса қандай да бір апериодты процессті сипаттайды. Екінші жағдай детерминді хаос режиміне жауап береді. Шынымен де, детерминизмнің негізгі принципін көруге болады: болашақ бастапқы күймен бірмәнді анықталады. Алайда, жүйенің эволюция процесі күрделі және периодты емес. Сырттан қарағанда ол кездейсоқ процесстен айырмашылығы болмайды. Алайда, егежей-тегжейлі талдау кезінде бұл процесстің кездейсоқ процесстен маңызды ерекшелігі анықталады: бұл процесс қайта қалпына келетін процесс. Шынымен де, бастапқы күйді тағы да қайталау арқылы детерминдеу күшіне біз тағы оның күрделілігінің дәрежесінен тәуелсіз тура сондай траекторияны жүргізе аламыз. Яғни, бұл периодты емес процесс хаосты анықтау кезінде хаосты болып табылмайды. Себебі ол күрделі, кездейсоққа ұқсас, бірақ дегенмен де детерминді процесс. Бұл жердегі ең маңыздысы, ол тұрақсыздықпен сипатталады және бұл жағдай бізге детерминді хаостың тағы бір маңызды қасиетін түсінуге мүмкіндік береді, ол - араласу [3] .
1. 2 Хаостық генераторлар
Динамикалық хаосты радиобайланыста және радиолокацияда қолдану берілген статистикалық, спектралды және басқа да қасиеттері бар хаостық тербелістер көзін жасауды талап етеді. Мұндай қорек көздерін хаос генераторлары деп атаймыз. Электромагнитті хаос генераторларын жасау есебі өзіне генератор құрылысының жасалуын, математикалық моделін, жүйенің хаостық әрекетінің мүмкіндік фактін орнатуды, сол әрекетке алып келетін бифуркациялық құбылысты оқуды қосады. Хаос генераторларын жасау кезінде айтылып өткен есептермен қатар тиісті спектралды және статистикалық қасиеттерге ие бола алатындай шарттарды табу есебі шешілуі керек. Хаос көздерінің электронды құрылғылар түрінде жасалынатын көптеген сандарының ішінен кейбіреулерін қарапайым хаос генераторының прототипі ретінде де қарастыруға болмайды.
Біріншіден, олардың көпшілігі тұтас емес қуат спектрлері бар хаостық тербелістерді генерациялайды. Ал практида, типтік талаптардың бірі ол -генерациялау жолағындағы спектрлік тығыздықтың тең мөлшерде бөлісуі болып табылады.
Екіншіден, көптеген хаос көздері онда қолданылатын элементтердің ерекшеліктеріне байланысты электромагнитті спектрдің төменгі жиіліктік (10-100 МГц-ке дейін) аймағында ғана жүзеге асырылуы мүмкін. Технологиядағы прогресс жиілікті шекараны ақырындап үлкен жиіліктер жағына жылжытқанымен, бұл шектеулер қандай да бір орын алады.
Үшіншіден, практикалық жағынан хаостық генераторлардың «элементтік базасы» негізінен классикалық электронды компоненттерден тұру керек. Жиі жағдайда, активті элементтер ретінде биполярлы және өрістік транзисторларды қолданған жөн [4] .
Хаос генераторлары екі классқа жіктеледі: үздіксіз және дискретті. Үздіксіздік және дискреттілік ұғымдары хаостық жүйелердің математикалық модельдерінің уақыттық айнымалысына қатысты болады [5] .
Қазіргі уақытта динамикалық хаос негізіндегі информациялық технологияларда ақпаратты жіберу, өңдеу, сақтау және қорғау үшін қолданылады. Байланыс жүйесіндегі жаңа бағыттардың бірі ақпаратты турахаосты байланыс жүйелерінің көмегімен жүзеге асыру болып табылады. Турахаосты байланыс жүйелерінің негізгі ұғымы хаостық радиоимпульс түсінігі болып табылады. Мұндай импульстің жиілік жолағы хаос көзінен генерацияланатын шығыс хаостық сигналдың жиілік жолағымен анықталады. Маңыздысы, кең шекара кезінде импульс ұзақтығына тәуелді болмайды. Бұл хаостық радиоимпульсті классикалықтан ерекшелендіреді. Хаостық радиоимпульстер турахаосты байланыс жүйелерінде тасымалдаушы тербелістер ретінде ақпаратты тарату үшін қолданыла алады. Ақпарат хаос көзінің параметрлерін модуляциялау жолымен АЖЖ-диапазонында генерацияланатын хаостық сигналға енгізіледі, ал хаосты сигналдан аралық жиілікті қолданбау жолымен ажыратылады. Турахаосты байланыс жүйелерінің негізгі элементтері хаостық радиоимпульстер генераторлары болып табылады.
Қазіргі уақытта аса жоғары жиілікті (АЖЖ) диапазондағы хаос генераторларының ішіндегі ең көп таралғандарының қатарына активті элемент ретінде диод және өрісті транзисторларды қолданатын қатты денелі генераторлар жатады. Мұндай хаосты радиоимпульсті генераторлардың кемшілігі өте аз шығыс қуаты болып табылады, ол - бірнеше он милливатт болады.
Турахаосты байланыс жүйелерінің схемасында:
а. хаос генераторы хаостық тербелістерді берілген микротолқындық диапазон жиілігінде генерациялайды;
б. информациялы сигналды хаостыққа енгізу хаостық радиоимпульстерді формалау жолымен жүзеге асырылады;
в. ақпаратты АЖЖ сигналдан ажырату жиіліктің аралықты түрлендіруінсіз жүзеге асырылады [6-8] .
Лоренц моделі.
Әуейі аттракторы бар динамикалық жүйелердің алғашқыларының бірі 1963 жылы америкалық метеоролог Э. Лоренц ұсынды. Ғылым әлемінде бұл тақырып қызу талас тудырып, ғылыми зерттеулер мен жарыққа шыққан ғылыми еңбектер саны күннен-күнге артып келеді. Аталған модельге қызығушылықтың көбеюінің көп себептерінің бірі, Лоренцтің дифференциалдық теңдеулер жүйесінің шешімінің траекториясы хаостық сипатта болуы. Э. Лоренцтің дифференциалдық теңдеулер жүйесі - бұл үшөлшемді сызықты емес автономды бірінші ретті дифференциалдық теңдеулердің келесі түрдегі жүйесі [9] :
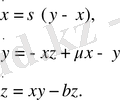 (1. 1)
(1. 1)
Лоренц моделінде үш тәуелсіз айнымалы бар: x(t), y(t) и z(t), сонымен қатар, бірнеше параметрлер болады. Біз үшін ең басты параметр ол μ. Бұл параметрдің өзгеруі кезінде динамикалық жүйе өзінің аттракторының типін өзгертеді. μ параметрінің бір мәндері кезінде жүйе тұрақты межелі нүктеге ие болады, ал μ-дың басқа мәндері кезінде, μ*-дың бифуркациялық үлкен мәнінде жүйе нанғысыз шешіміне ие болады.
Лоренц теңдеулер жүйесінің шешімі μ параметрі бифуркациялықтан асқанда, классикалық кездейсоқ процесс секілді болады. Қандай да бір мағынада, Лоренц аттракторы стохасты автотербелістер болып табылады, олар динамикалық жүйелерде сыртқы көздің есебінен қолдау алады. Фазалық кеңістікте әуейі аттрактор қандайда бір траектория топологиясына ие болады, оның шегінде екі аймақты ерекшелеп алуға болады. Уақыттың әр моментінде теңдеудің шешімі осы аймақтардың біреуінде болады.
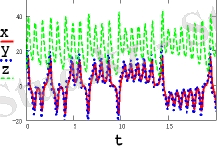
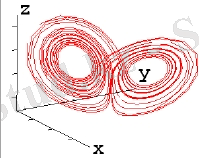
Әуейі аттракторлардың тағы бір тамаша қасиеті (жиі жағдайда Лоренц аттракторында) оның бастапқы шартқа деген сезімталдығы. Бұрындары зерттелген аттракторлар, қозғалмайтын нүктелер немесе шекті циклдер әртүрлі бастапқы шарттар үшін шешімдері бір асимптоталық мәніне келетіндігімен сипатталатын. Басқаша айтқанда, әртүрлі бастапқы шарттарға сәйкес келетін әртүрлі нүктелерден шыққан түрлі траекториялар t→∞ кезінде бір нүктеге келетін немесе жақын қисықтар түрінде болатын. Сондықтан да, қозғалмайтын нүктелерден құралған аттракторларға және шекті циклдерге ие қарапайым жүйелердің қозғалысы өте үлкен уақыт кезінде жақсы анықталады. Ал әуейі аттракторлармен барлығы олай емес. Қандай болсын жақын мәнді бастапқы шарттарды алсақ та, t→∞ кезінде шешім фазалық кеңістікте бір-бірінен кете отырып таралады. Нағыз есептерде бастапқы шарттар қандай да болсын ауытқулармен белгілі болса, жеткілікті үлкен t уақытында әуейі аттрактордың қозғалысын көрсету мүмкін емес, сондықтан да әуейі аттракторлармен сипатталатын жүйелердің қозғалысын айту мүмкін емес. Лоренцтің өзі айтып кеткендей динамикалық жүйе траекториясының дәл осы түрімен бірнеше апта бұрын ауа райын болжау мүмкін еместігі байланысты болуы мүмкін.
Э. Лоренцтің дифференциалдық теңдеулер жүйесін компьютерлік модельдеу және оны сандық есептеу нәтижесінде, Лоренц аттракторының барлығын және жүйенің траекториясының μ параметрінің өзгеруіне сәйкес спиральды тұзақ болатынын көрсету қажет [10] .
Ресслер моделі.
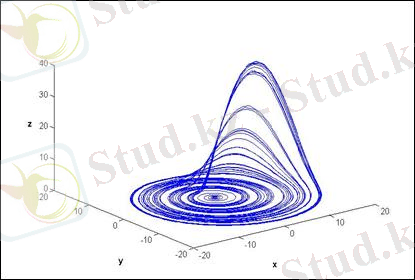
Келесі жүйені неміс зерттеушісі Ресслер 1976 жылы ұсынған. Бұл модель периодты және хаостық қозғалысты сипаттайды. Ол дифференциалды тедеудің төмендегідей автономды жүйесін ұсынды. Содан бері ол бейсызық динамиканың классикалық объектілерінің бірі болып қызмет етеді. Жүйенің түрі [11] :
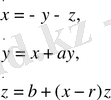 (1. 2)
(1. 2)
Бұл жердегі x, y, z - динамикалық айнымалылар , a, b, r - параметрлер.

Чуа тізбегі (схема) .
Чуа тізбегі - хаостық тербелістердің режимдерін демонстрациялайтын қарапайым электрлік тізбек. Бұл тізбекті Калифорния университетінің профессоры 1983 жылы Леон Чуа ұсынған. Тізбек екі конденсатордан, бір индуктивтілік катушкадан, сызықты резистордан және кері кедергісі бар бейсызық резистордан тұрады (әдетте Чуа диоды деп аталады) . Чуа тізбегі Лоренцтің электронды жүйе моделімен жасалынған сәтсіз тәжірибесінен кейін ойлап табылды. Лоренцтің де, Ресслердің де хаос пайда болу жүйелеріндегі негізгі механизмі - тепе-теңдіктің тұрақсыз жағдайының бірден көп болуы. (Лоренц үшін үш, Ресслер үшін екі), онда осы қасиеттерге ие қарапайым тізбекті құрауға болады [12] . Нәтижесінде сурет 1. 8-де көрсетілгендей схема шықты. Бұл қарапайым бифуркация ретін және хаосқа ауысуды демонстрациялайтын қарапайым тербелмелі тізбек. Тізбектің теңдеуі:
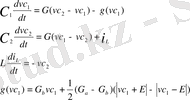 (1. 3)
(1. 3)
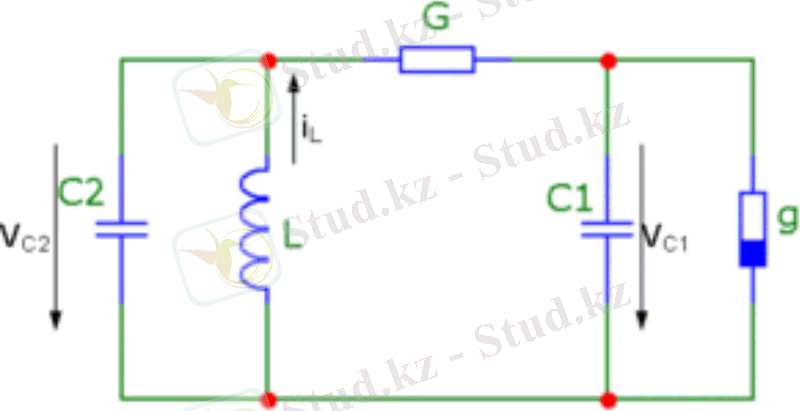
Бұл қатынас графикалық түрде сурет 1. 9-да келтірілген. Резистордың кедергісі N R , яғни Чуа диоды бейсызық функциямен оның шығысындағы кернеуден тәуелді болады [13] .
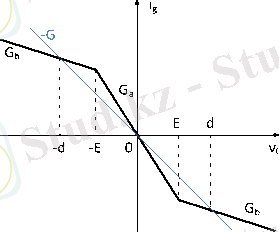
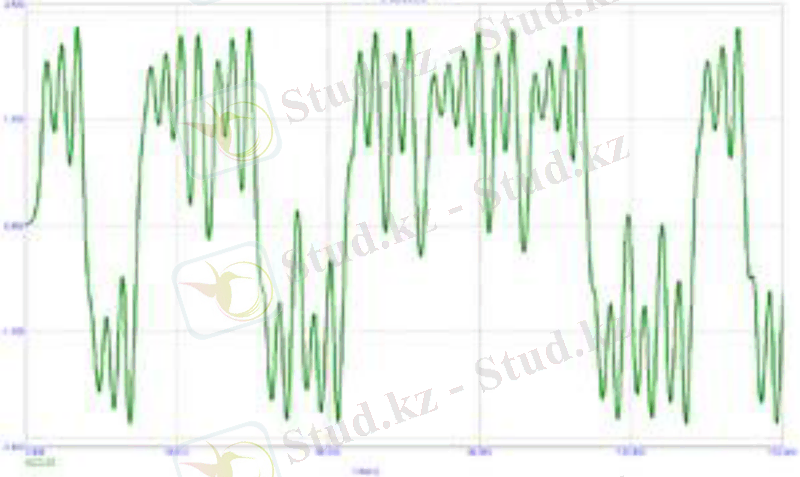
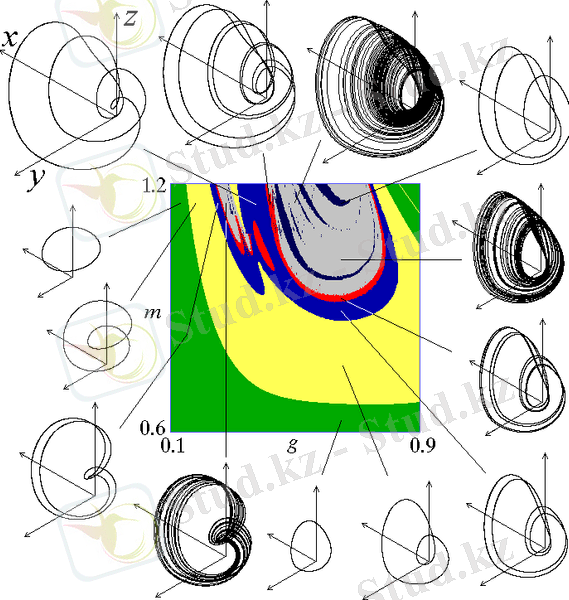
Чуа тізбегі параметрлердің жеткілікті тар аймағындағы тербелістердің хаостық режимдерін анықтайды. Сурет 1. 10-да тербелістердің негізгі режимдері келтірілген.
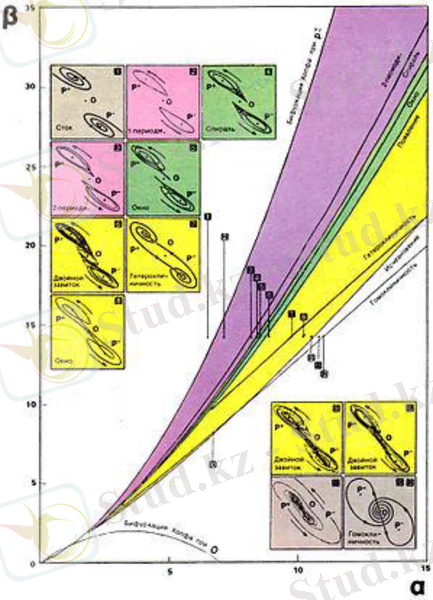
(а)

(б) (с)
Сурет 1. 10. m0=-8/7, m1=-5/7 кезіндегі режимдердің бифуркациялық диаграммасы (a), L=1/7Гн; G=0. 7См; C1=1/9Ф; C2=1Ф; Ga=-0. 8А/В; Gb=-0. 5А/В жағдайы үшін vC1 -дің уақыттық тәуелділігі(б), Қос айналым типіндегі аттрактор. L=1/7Гн; G=0. 7См; C1=1/9Ф; C2=1Ф; Ga=-0. 8А/В; Gb=-0. 5А/В кезіндегі Лиссажу фигурасы (c) [13]
Анищенко - Астахов генераторы.
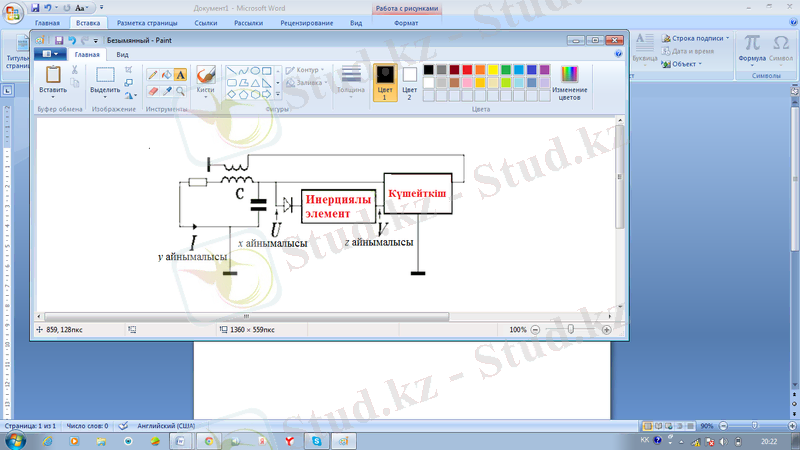
Электроникадағы детерминді хаостың классикалық моделі Анищенко-Астахов автогенераторы болып табылады. Бұл генератор 1981 жылы ұсынылды. Модельдеу процесі кезінде активті бейсызық элементтегі (активті кедергі) таралатын қуаттың ондағы тербеліс типінен тәуелділігі орнатылды. Төмендегі сурет 1. 11-де келтірілгендей жүйедегі автотербеліс контурға R(T) активті кедергіні орнату арқылы қамтамасыз етіледі, оның қасиеті бейсызық және инерциялық жолмен одан өтетін тоқтан тәуелді болады. Инерциялық бейсызыққа ие Анищенко-Астахов генераторының блок схемасы төменде көрсетілген [14] :
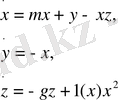 (1. 4)
(1. 4)
1. 3 Заманауи хаос генераторларының қолданыс аясы
Практикада хаостық тербелістер ақпаратты тарату және қорғау үшін қолданылады. Олардың шығыс сигналы генерация параметрлерінің өзгерістің кең аймағында болуын және кеңжолақтылық параметрлерін қанағаттандыру керек. Мәліметтерді жасырын тасымалдаудың көптеген әдістері бар. Солардың бірі хаостық маскировка болып саналады. Бұл информациялық сигналдың бейсызық араласуы, хаостық режимдердің ауысуы және басқарушы параметрлерді модульдеу және т. б. болып табылады.
Хаостық маскировка дегеніміз - мәліметтерді жіберуді жасырудың ең қарапайым және бірінші әдістерінің бірі болып табылады [15] . Бұл әдістің принципиалды схемасы сурет 1. 13-те келтірілген. m(t) информациялық сигнал таратқыш жағында сумматорда генерациялайтын x(t) хаостық таратқыш жүйенің тасушы сигналға қосылып, ары қарай байланыс каналы бойынша жіберіледі. Қабылдағышта қабылданатын сигналдың көмегімен u(t) хаостық генераторы бар толық синхронизация жүзеге асады. Нәтижесінде қабылдағыш генератордың динамикасы таратқыштың динамикасымен бірдей бола бастайды. Детектрленген сигнал қабылдағыштағы хаос генераторының синхронды белгісі және қабылданатын сигнал арасындағы айырым секілді азайтқыш құрылғыдан өткеннен кейін пайда болады.
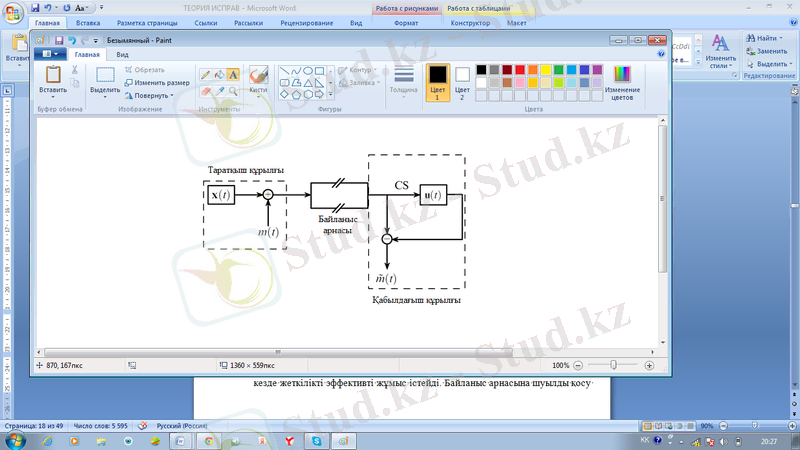
Ақпаратты жасырудың мұндай схемасы байланыс арнасында шуыл жоқ кезде жеткілікті эффективті жұмыс істейді. Байланыс арнасына шуылды қосу жіберілетін ақпарат сапасының күрт төмендеуіне, одан өзге, басқарушы параметрлерге өзгерістер енгізу шығысында қосымша шуылдардың пайда болуына алып келеді.
Хаостық синхронизация құбылысын қолдану арқылы ақпаратты тасымалдаудың әртүрлі әдістері жүзеге асады және олар радиотехникалық жүйелердің негізінде орындалады. Ақпаратты жасырын жіберудегі алғашқы схемалардың бірі хаостық маскировка схемасы болды. Сондықтан да көптеген эксперименттік жұмыстар осы схема негізінде жасалынды. Төменде сурет 1. 14-те келтірілген схеманың жұмыс жасау сипаттамасына тоқталсақ: m(t) тесттік информациялық сигнал биттердің тізбектілігін көрсетеді, бұл сигнал таратқыш генератордың параметрлерін және (t) қайта қалпына келтірілген сигналдың квадратын модуляциялайды. Сигналдың m=0 күйі қабылдағыш құрылғының толық синхронизациясына, m=1 - асинхронды динамикаға сәйкес келеді. Бұл жүйе цифрлы сигналды да тарату мүмкіндігі бар екенін көрсетеді [16] .

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz