Термодинамиканың І және ІІ заңдары: ішкі энергия мен энтальпия, Гесс заңы, энтропия және химиялық тепе-теңдік


1. Термодинамиканың І-ші заңы тұрғысынан ішкі энергия, жылу және жұмыс арасындағы байланысты сипаттаңыз, 1-ші заңның анықтамаларын келтіріңіз, ішкі энергия мен энтальпияның өзара байланысын көрсететін теңдеуді талдаңыз.
Термодинамика - температура мен жылудың және жылу мен жұмыстың өзара байланысын зерттейтін ғылым. Термодинамикада зерттелінетін негізгі құбылыстар:
1. Энергияның бір денеден екінші денеге және бір түрден екінші түрге ауысуы.
2. Әртүрлі жағдайларда өтетін физикалық және химиялық процестердің энергиялық эффектілері.
3. Процестің өтуі не өтпеуі, олардың бағыты және шегі. I ші термодинамиканың заңы М. В. Ломоносов 1748 ж. ашқан жалпы энергия сақталу заңының салдары болып келеді.
- Энергия жойылмайды, жоқтан пайда болмайды, ол тек қана бір түрден басқа түрге қатаң эквивалентті мөлшерде ауысады.
- Кез-келген оқшауланған жүйеде энергияның жалпы қоры тұрақты сақталады.
3. I ші текті мәңгілі қозғалтқыш болуы мүмкін емес. Кез-келген процесс үшін жүйенің ішкі энергиясының көбеуі ∆U=U 2 -U 1 жүйеге берілген жылу мөлшері мен жүйемен атқарылған жұмыс мөлшерінің (А) айырымына тең.
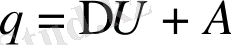 (1. 6)
(1. 6)
Шексіз аз мөлшерінде жүретін процестер үшін термодинамиканың I ші заңы келесі түрде жазылады:
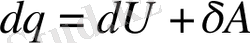
Термодинамиканың бірінші заңы энергияның сақталу заңының ж/е бір түрден екінші түрге өту заңының Термодинамикалық жүйе үшін біріктірілген түрі. Осылайша оны келесі түрде тұжырымдауға болады: оқшауланбаған термодинамикалық жүйенің ΔU ішкі энергиясының өзгерісі жүйеге берілген Q жылу мөлшерімен жүйенің сыртқы ортаға жасаған А жұмысының айырымына тең. ΔU= Q - A
Бұл теңдікті көбіне мына түрде жазады: Q = ΔU- A . Оны тұжырымдасақ: жүйенің сыртқы ортадан алған жылу мөлшері оның ішкі энергиясының өзгеруіне ж/е сыртқы ортаға кететін жұмысты өндіруге жұмсалады.
Осы заңға сйкес энергия жоқтан пайда болмайды ж/е жоққа жұмсалмайды; ол бір жүйеден екінші жүйге өтеді ж/е бір түрден екінші түрге кетеді. Бірінші заңның ең маңызды салдары бірінші текті мәңгі қозғалтқыш жасау мүмкін емес екендігі туралы тұжырым болып табылады. Ол дегеніміз сыртқы ортадан ешқандай энергия қабылдамай ж/е өзінің ішінде ешқандай өзгерістер жүрмей пайдалы жұмыс өндіретін машина жасау мүмкін емес. Бұндай машина жасау әрекеттері әрдайым сәтсіздіктермен аяқталған. Кез-келген машина А пайдалы жұмысты тек сыртқы ортадан Q жылу алу арқылы н/е ΔU ішкі энергияның кемуі есебінен жүзеге асырылады.
Енді термодинамиканың бірінші заңын идеал газдардағы изопроцестер үшін қолданайық:
- Изохоралық процестерде(V=const) газ жұмыс жасамайды А=0, сәйкес
Q = ΔU = U T1 - U T2
Бұндағы U T1 ж/е U T2 газдың бастапқы ж/е соңғы күйдегі ішкі энергиялары. Идеал газдардың ішкі энергиясы тек температураға тәуелді ( Джоуль заңы) . Изохоралық қыздыру кезінде газ жылуды жұтады(Q>0) ж/е оның ішкі энергиясы артады. Ал суытқан кезде(Q<0) жылу газдан сыртқа бетіледі, сәйкес ішкі энергия кемиді.
- Изобаралық процестерүшін (p=const) газдың жасайтын жұмысы былай өрнектеледі:
A = p (V 2 -V 1 ) = pΔV
Ал термодинамиканың бірінші заңы бұндай процесс үшін : Q = U T1 - U T2 + p (V2 -V1) = ΔU - pΔV
Изобаралық ұлғаю кезінде (Q>0) газ жылуды жұтып, оң жұмыс жасайды. Ал изобаралық сығылу кезінде (Q<0) жылу сыртқы ортадан газға беріледі. Нәтижесінде А<0 . Изобаралық сығылу кезінде газ температурасы кемиді Т 2 <Т 1 , ішкі энергия азаяды ΔU<0.
- Изотермиялық процестерде газтемпературасы өзгермейді, сәйкесінше ішкі энергияда өзгермейдіΔU =0. Изотермиялық процестер үшін термодинамиканың бірінші заңыкелесі теңдікпен беріледі : Q = A. Изотермиялық ұлғаю кезінде алынған жылу сыртқы ортаға жұмсалатын жұмысқа кетеді. Ал сығу кезінде газды сығуға кеткен күштер сыртқы ортаға берілетін жылуға айналады.
Термодинамикада изопроцестермен қатар адиабаталық процестер қарастырылады. Адиабаталық процес - сыртқы ортамен жылу алмасу болмайтын процесс. Оған адиабаталық ұлғаю және сығылу процестері жатады. Бұндай процестерде Q = 0, сондықтан термодинамиканың бірінші заңы былай өрнектеледі: A = - ΔU. Яғни газ ішкі энергиясының кемуі есебінен жұмыс жасайды. Адиабаталық ұлғаю кезінде газ оң жұмыс жасайды, сондықтан оның ішкі энергиясы кемиді, осыдан газ температурасы төмендейді. Нәтижесінде адиабаталық процесс кезінде изотермиялық процеске қарағанда қысым тезірек төмендейді.
Ішкі энерия - денені құратын бөлшектердің кинетикалық және потенциалдық энергияларының қосындысы. Кинетикалық энергия бөлшектердің хаосты жылу қозғалысының нәтижесі. Жылу қозғалысы температурамен байланысты. Дененің потенциалдық энергиясы бөлшектердің бір-бірімен әрекеттесуіне байланысты. Бөлшектер арасында тартылу ж/е тебісу күштері болады. Құрамы бір текті денелердің ішкі энергиясы оның массасына, бөлшектердің жалпы санына пропорционалды, яғни дененің энергиясы аддитивті шама. Толық әшкә энергияны беретін энергия түрлері молекула, атом, электрон, протон, т. б. элементарлы бөлщектердің өзара әсерлесуімен байланысты. Сондықтан дененің ішкі энергиясының абсолютті мәнін табуға болмайды.
Энтальпия н/е жылу эффектісі - жүйенің онда болған химиялық өзгерістер нәтижесінде сіңірген н/е бөліп шығарған жылу энергиясының мөлшері. Энтальпия Q р н/е ΔH пен белгіленеді (Q р = - ΔH) . Жылу бөлінетін реакциялар ( ΔH<0) - экзотермиялық, ал сіңіретін реакциялар ( ΔH>0) - эндотермиялық зеакцияларға жатады. Жылу эффектісі көрсетілген реакция теңдеуі термохимиялық болып табылады:
CH 4 + 2O 2 = CO 2 +2H 2 O + -ΔH.
Химиялық заттардың түзілу жылулары стандартты жағдайларда алынады. Стандартты түзілу энтальпиясы - стандартты жағдайда 1 атм. Қысымда, жай заттардан бір моль затты алу кеткен жылу мөлшері.
Енді оның ішкі энергиямен байланысын көрсету үшін термодинамиканың бірінші заңының өрнегін пайдаланымыз: Q = ΔU - pΔV → Q = U T1 - U T2 + p V 2 -рV 1 → Q =(U T2 + p V 2 ) - ( U T1 +рV 1 )
Бұндағы p ж/е V жүйені сипаттайтын параметрлер, ал U жүйенің күй функциясы. Олай болса, U+рV шамасы да күй функциясы, ал оның өзгеруі процестің жолына тәуелсіз болады, ол тек процестің бастапқы ж/е соңғы күйімен байланысты. Бұл Н =U + p V теңдігі энтальпияға тең.
H 2 - H 1 = ΔH = Q P ж/е U 2 - U 1 =ΔU = Q V. Яғни энтальпия ΔH = Q P тұрақты қысым кезіндегі жылу эффектісі, ал ішкі энергия ΔU = Q V тұрақты көлем кезіндегі жылу эффектісі.
Энтальпия өзгерісі тәжірибе жолымен оңай анықталады. Сол себепті бұл функцияны термодинамикада жиі қолданады. Ішкі энергияның да, энтальпияның да абсолют мәні табылмайды, оның тек соңғы өзгерісін ғана анықтауға болады. Екеуі де экстенсивті қасиеттерге жатады, яғни қосылады
2. Гесс заңын термодинамикалық тұрғыдан негіздеңіз, термохимиялық есептеулерде Гесс заңының салдары қалай қолданылатынын көрсетіңіз.
Гесс заңы химиялық реакцияның жылу эффектісін сипаттайды. Реакцияның жылу эффектісі - жүйенің онда болған химиялық өзгерістер нәтижесінде сіңірген н/е бөліп шығарған жылу энергиясының мөлшері. Жылу эффектісі Q н/е ΔH пен белгіленеді (Q= - ΔH) . Жылу бөлінетін реакциялар (Q>0, ΔH<0) - экзотермиялық, ал сіңіретін реакциялар (Q<0, ΔH>0) - эндотермиялық зеакцияларға жатады. Жылу эффектісі көрсетілген реакция теңдеуі термохимиялық болып табылады: CH 4 + 2O 2 = CO 2 +2H 2 O + Q (-ΔH) Термохимиялық есептеулердің негізінде Гесстің жылу мөлшерінің тұрақтылығы заңы жатыр: Процестің жылу эффектісі процестің өту жолына тәуелсіз, ол тек жүйенің бастапқы ж/е соңғы күйлерімен анықталады. Бұл заң термодинамиканың бірінші заңының тікелей салдары болып табылады. Бұл заңға сәйкес химиялық реакция жылуы реакция өнімдерінің түзілу жылуларының қосындысы мен бастапқы заттардың түзілу жылуларының қосындысының айырымына тең: Q реакц = Q түз. өнім - Q түз. б. з. Мұндағы Q түз - 1 моль қосылыстың стандартты жағдайларда ( T =298K, p = 1атм. ) жай заттардан түзілу жылуы. Q түз = -ΔН 0 дегеніміз заттың стандартты молярлық түзілу жылуы. Тұрақты модификациалы жай заттардың стандартты түзілу жылуы нөлге тең.
Гесс заңының орындалуы мынадай екі шартпен байланысты: 1- жүйеде тек көлем ұлғаю жұмысы жасалуы керек, ол сыртқы қысымға қарсы жұмсалатын жұмыс; 2 - процесс не қысым не көлем тұрақты жағдайда өтуі керек. Гесс заңына мысал ретінде аммоний хлоридінің судағы ерітіндісін алудың жолын қарастырайық. Бұл ерітіндіні екі жолмен алуға болады. Бірінші жол:
NH 3 (газ) + aq NH . 3 *aq + ΔH 1
HCl (газ) + aq HCl*aq + ΔH 2
NH . 3 *aq + HCl*aq NH 4 Cl*aq + ΔH 3
Екінші жол: NH 3 (газ) + HCl (газ) NH 4 Cl (қатты) + ΔH 4
NH 4 Cl (қатты) + aq NH 4 Cl*aq + ΔH 5
Гесс заңы бойынша ΔH 1 + ΔH 2 +ΔH 3 = ΔH 4 + ΔH 5 .
Гессзаңынан мынадай қорытындылар алуға болады:
- Заттың түзілу жылуының мәні оның алғашқы заттардан алыну жолына тәуелді емес;
- Заттың алғашқы заттарға ыдрайу жылуы оның осы заттардан түзілу жылуына тең, тек таңбалары қарама-қарсы.
- Екі түрлі жүйедегі өтетін процестердің нәтижесінде бірдей заттар түзілетін болса бұл процесстер жылуларының айырымдары біреуінің екінші күйге ауысу жылуына тің болады.
Гесс заңы - процестің жылу эффектісі процестің өту жолына тәуелсіз, ол тек жүйенің бастапқы ж/е соңғы күйлерімен анықталады. Бұл заңға сәйкес химиялық реакция жылуы реакция өнімдерінің түзілу жылуларының қосындысы мен бастапқы заттардың түзілу жылуларының қосындысының айырымына тең: Q реакц = Q түз. өнім - Q түз. б. з. .
Ал бұл заңнан шығатын салдар: 1- Заттың түзілу жылуының мәні оның алғашқы заттардан алыну жолына тәуелді емес; 2-Заттың алғашқы заттарға ыдрайу жылуы оның осы заттардан түзілу жылуына тең, тек таңбалары қарама-қарсы. 3- Екі түрлі жүйедегі өтетін процестердің нәтижесінде бірдей заттар түзілетін болса бұл процесстер жылуларының айырымдары біреуінің екінші күйге ауысу жылуына тең болады.
Гесс заңына негізделіп белгісіз реакциялардың, тіпті іс жүзінде жүрмейтін реакциялардың жылу эффектілерін есептеуге болады. Ол үшін келесі әдістерді пайдалануға болады:
а. Химиялық реакцияларды үйлестіру арқылы керекті реакцияның жылу эффектісін табу әдісі. Мысал қарастырайық. Берілген реакциялардың жылу эффектісі берілген дейік:
1. С (графит) + О 2 (газ) = СО 2 (газ) + ΔН 1
2. СО(газ) +1/2 О 2 = СО 2 + ΔН 2
Осы екі реакция арқылы
. С (графит) + 1/2О 2 (газ) = СО (газ) реакциясының жылу эффектісін табуға болады, ол үшін бірінші теңдеуден екінші теңдеуді алып тастаймыз: . С (графит) + О 2 (газ) - СО(газ) - 1/2 О 2 = СО 2 - СО 2
С (графит) + 1/2О 2 (газ) - СО(газ) = 0
С (графит) + 1/2О 2 (газ) = СО(газ) Сонда бұл реакцияның жылу эффектісі ΔН 3 =ΔН 1 - ΔН 2
ә. Реакцияға қатысқан заттардың жану жылуларының көмегімен реакцияның жылу эффектісін табу әдісі. Гесс заңынан шығатын салдар бойынша реакцияның жылу эффектісі реакцияға қатысатын заттардың жану жылуларының алгебралық қосындысына тең. Заттың жану жылуы деп осы заттың оттегімен әрекеттесіпжоғарғы оксидтер бергендегі реакцияның жылуы. Жану жылуы 1 моль затқа келтіріледі. Реакцияның жылу эффектісі реакцияға түскен заттардың ж/е реакция өнімдерінің жану жылуларының қосындысының айырымына тең. : ΔH r o = ΣΔ H С 0 , 298 , (түскен зат) - ΣΔН С 0 , 298 , (шыққын зат) . Мысал қарастырайық: ацителеннен 298К де бензолдың түзілу реакциясының жылу эффектісін табу керек. Ол үшін ацителеннің ж/е бензолдың жану жылуларын білу керек 3С 2 Н 2 (газ) = С 6 Н 6 (сұйық) Осы жерде ΔН r 0 , 298 , = 3 ΔН С 0 , 298 , (С 2 Н 2 ) - ΔН С 0 , 298 (С 6 Н 6 )
б. Реакцияға қатысатын заттардың түзілу жылуларының көмегімен реакцияның жылу эффектісін табу әдісі. Гесс заңынан шығатын тағы да бір салдар бойынша реакцияның жылу эффектісі реакцияға қатысатын заттардың түзілу жылуларының алгебралық қосындысына тең. Заттың түзілу жылуы деп жай заттардан 1 моль зат түзілгендегі жылуды аламыз. Анықтамалықтарда келтірілген заттардың түзілу жылулары стандартты жағдайларда алынады. Стандартты жағдайда ол ΔН f 0 , 298 деп белгіленеді. . Реакцияның жылу эффектісі реакция өнімдерінің ж/е реакцияға түскен заттардың жану жылуларының қосындысының айырымына тең. : ΔH r o = ΣΔ H f 0 , 298 , (шыққын зат) - ΣΔН С 0 , 298 , (түскен зат) . Мысал қарастырайық С 2 Н 4 (газ) + Н 2 О (газ) =С 2 Н 5 ОН (газ) , Осыдан этанолдың түзілу реакциясының жылу эффектісі ΔН r 0 , 298 , = ΔН f 0 , 298 , (С 2 Н 5 ОН) - {ΔН f 0 , 298 (С 2 Н 4 ) + ΔН f 0 , 298 (Н 2 О) }
3. Термодинамикалық ІІ-ші заңының анықтамалары мен теңдеулерін келтіріңіз. Энтропияны процесс бағытының критериі ретіде қолдануды көрсетіңіз.
Бағыты мен оның жүру шегін анықтауда терм-ң 1ші заңы жеткіліксіз б-ды. Бұл терм-ң 2ші заңының орнатылуына себеп болды. Терм-ң 2ші бастамасы оның 1ші бастамасы секілді постулат болып табылады. Яғни одан шығатын тұжырымдамалардың барлығы осы күнге дейін тәжірибеде дәлелденіп келеді. 1824ж С. Карно терм-ң 2ші бастамасының негізгі қағидасын орнатты. XIXғ ортасында Клаузиус, Томсон мен Максвелл терм-ң 2ші заңы табиғаттың жалпы заңдарының бірі екенін атап өтті.
Терм-ң 2ші заңының көптеген анықтамалары бар. Олардың барлығы бір-біріне тең шамалы ж/е логикалық түрде тұжырымдалады. Анықтамаларға тоқталсақ.
Клаузиус анықтамасы:жылу өздігінен, яғни ешқандай теңесусіз, суық денеден ыстық денеге ауыспайды. Ал ауысатын б-са, онда міндетті түрде жүйеде қосымша өзгерістер б-ды.
Томсон анық-сы:ешқандай процестердің арақатынасы тек жылудың жұмысқа өтуіне негізделмейді, ал жұмыстың жылуға айналуы процестердің жалғыз нәтижесі болуы мүмкін.
Оствальд анық-сы:Екінші текті мәңгілік қозғалтқтышты құру мүмкін емес. Екінші текті қозғалтқыш ретінде тек сыртқы ортадан берілетін жылу арқылы ғана жұмыс жасайтын машина қарастырылады.
Енді осы анықтамаларды мағынасын түсіндірсек. Негізінде жылудың жұмысқа өтуі мүмкін. Ол процес кез-келген жылулық машиналардың жұмысы кезінде өтеді. Яғни машина өз жұмысын белгілі бір жылубергіштен жылу сіңіруі арқ жасайды. Бірақ жұмыс денесі алатын q 1 жылуы жұмысқа толығымен айналмайды, оның бір бөлігі ғана А= q 1 - q 2 . Ал жылудың қалған бөлігі q 2 темп-сы төмен денеге өтеді(жылуқабылдағыш) . Қорыта айтқанда ондай машинаның жұмысы бірмезгілде жылубергіштен q 1 жылуын алып А жұмысын жасау мен белгілі бір q 2 жылуын темп-сы төмен жылуқабылдағышқа беруге негізделеді.
Жасалынған жұмыс мөлшерінің жұмыс денесіне жылубергіш 0берген q 1
жылу мөлшерінің қатынасы пайдалы әсер коэффиценті деп аталады. Осы шаманы қолдана отырып терм-ң 2ші заңына мынадай анықтама беруге болады:жылулық машинаның ПӘК-нің ең үлкен мәні жұмысқа қатысатын дене мен заттың табиғаты мен түріне тәуелді емес, ол тек қана жылубергіш пен жылуқабылдағыштың темп-на тәуелді.
Терм-ң 2ші заңын математиккалық түрде өрнектеу үшін Карно циклі деп аталатын термодинамикалық цикл қарастырылады. Терм-ң 2ші заңы Карно циклінің ПӘК-і тең болатынын қатаң түрде көрсетеді.
Қайтымсыз процестер үшін энтропияның өзгерісі процестің жылуымен мына теңсіздіктер арқ н/е (1)
(2)
ж/е T (3)
байланысқан. Сондықтан мәліметтер б-ша қайтымсыз процестердің энтропиясын есептеуге болмайды. Бірақ қайтымды ж/е қайтымсыз процестерде энтропия өзгерісі бірдей б/ды, өйт энтропия күй функциясы. Сонда реал қайтымсыз процестің энтрописын есептеу үшін процесті ойша қайтымды етіп жүргізіп, қайтымды процес үшін энтропия теңдеуімен оның өзгерісін есептеуге б-ды. Әртүрлі процестер үшін энтропия өзгерісін есептеу:
1. Кез-келген заттың изотермиялық процесі үшін(Т=const) . Ойша изотермиялық процесті қайтымды етіп жүргізіп, энтропия өзгерісін мына теңдікпен есептейміз:
2. Тұрақты көлемде кез келген затты Т 1 темп-дан Т 2 темп-ға қыздырған кезде. Бұл жағдайда процестің жылуы күй функциясының қасиеттеріне ие б/ды ж/е процес жолына тәуелсіз б/ды. теңдігендегі шамасын теңдігіне қойсақ мына теңдік шығады:
Егер = const деп жуықтасақ, онда тең болады.
3. Тұрақты қысым кезде(p=const) :
Егер = constб/са, онда
4. Идеал газдарға арналған әртүрлі процестер үшін энтропия өзгерісі мына теңдіктерден шығады:
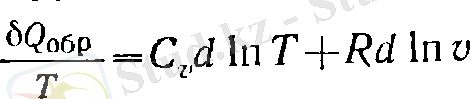 ж/е
ж/е
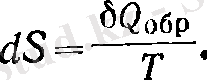
Сонда:
Егер = constб/са, онда
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz