Автотербелмелі жүйелер кластерінің сигнал өндіру режимдері және оларға шуыл мен флуктуациялардың әсерін тәжірибе жүзінде зерттеу

Пән: Автоматтандыру, Техника
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 41 бет
Таңдаулыға:

КІРІСПЕ

Осы жұмыста автотербелмелі жүйелер кластерінің сигнал өндіру режимдері және оларға шуыл мен флуктуациялардың әсері тәжірибе жүзінде зерттелді. Автотербелмелі жүйе ретінде ФитцХью-Нагумо [1] нейрон моделі таңдалды, ал кластер осы екі нейрон арасында сызықты-теріс байланыс арқылы құрылды. Нейрондар арасындағы байланыстың теріс болуы екі нейронның бір-біріне қарама-қарсы әсері арқылы сипатталады. Осыған байланысты бірінші нейрон екінші нейронға қоздырушы типті нейрон болса, екінші тежеуші қызметін атқарады.

Автотербелмелі жүйелер кластерінің динамикасын сипаттайтын дифференциалдық теңдеулер жүйесін аналитикалық шешімдерін тапқанда, жүйеде теңдеу орнықтылығының шекаралық шарты анықталды. Аталған шарт бойынша кластердің динамикасын сипаттайтын дифференциалдық теңдеулер жүйесінде берілген екі параметр мәндері арқылы жүйенің сигнал генерациялау режимдері басқарылады. Параметрлердің мәндерін өзгерту арқылы жүйенің орнықтылығын жоғалту шекарасында «қосжиілікті» Хопф [2] бифуркациясы анықталды. Сонымен қатар параметрлердің шекаралық шарттың кейбір кіші мәндерінде теорияда айтылмаған «bursting» [3] режимі анықталды. Теңдеу орнықтылығының шекаралық шартынан үлкен мәнінде тағы бір төртінші режим «тыныштық» деп аталатын режим анықталды.

Табиғатта және техникада бір-бірімен байланыста болатын және өзара әсерлесетін автотербелмелі жүйелер кең таралған. Осындай жүйелерде әрқашан шуылдар мен флуктуациялар болады. Осыған байланысты динамикалық жүйелерге шуылдардың әсерін зерттеу ғылыми маңызы зор болып табылады. Зерттеліп отырған автотербелмелі жүйелер кластеріне шуыл әсер еткенде, жүйеде қандай бифуркациялық құбылыстар орындалатыны осы жұмыста сандық және тәжірибе жүзінде зерттелді.

1. НЕЙРОН - АВТОТЕРБЕЛМЕЛІ ЖҮЙЕ

Нейрон динамикасын сипаттайтын математикалық модельдер

Жеке нейронның жұмысын атқаратын математикалық модельдерді жасау

алдыңғы ғасырдың ортасынан бастау алып келеді. Мұндай қызығушылық биологиялық қағидалар бойынша жұмыс істейтін, биологиялық тұрғыдан дәлме - дәл техникалық құрылғыларды жасауға болатын, биологиялық құрылымдарды математикалық модельдеу арқылы шешіледі.

Осы жұмыста барлық белгілі нейрондардың математикалық модельдерін сипаттау мақсаты қойылмаған. Аталған жұмыста орындалған жұмыстардың мазмұнына ең жақын болатын тек қана бірнеше нейрон модельдерін сипаттаймыз.

Қазіргі уақытта жеке нейрондардың көптеген математикалық модельдері жасалған. Ең алғашқы нейрон модельдерінің бірі 1907ж [4] «integrate-and-fire» ұсынылған Луи Лапиктің моделі болып табылады. Модель келесі теңдеулермен сипатталады:

\[I_{s y n}(t)=g\sum_{s p i t s}f(t-t_{s p i s})\]

\[f(t)=A[\exp(-\,t/t_{1})-\,\exp(-t/\tau_{2})]\]

(1. 1)

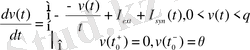мұндағы, V(t) - нейрондағы мембраналы потенциал; θ - спайктың өндірілу шегі; I _ext - синаптикалық токтардың қосындысы; τ ₁ және τ ₂ - синаптикалық токтарды сипаттайтын уақыттық константалар.

Нейрондағы мембраналы потенциал V(t) спайктың өндірілу шегіне θ жеткенде, импульс пайда болады. Осы импульстан кейін нейрон тыныштық күйіне қайтып келеді. Осы модельдің кемшілігі бар, ол кіріс токтың сызықты өсуіне байланысты жұмыс істеп кету жиілігінің шексіз үлкен сызықты өсуі болып табылады. Алайда, аталған модельді жақсарту мақсатында рефрактерлік период енгіземіз, ол әсер ету потенциалы пайда болғаннан кейін, белгілі бір уақыт аралығында жұмыс істеп кету жиілігін шектейді. Берілген модельдің үлкен жасанды нейрондық жүйелерді құруға қолайлы болатын жоғарғы есептеу тиімділігі бар. Әрине, осы модельдің негізгі кемшілігі де бар - импульс өндіру биофизикалық механизмдерін ескермеу болып табылады.

Аталған кемшілікті 1952 ж. Ходжкин және Хакслимен [5] ұсынылған математикалық модель шешеді. Модельдің негізгі ерекшеліктері бар, модель тәжірибелік мәліметтер бойынша құрастырылған, осыған байланысты нейрондағы пайда болатын импульстарды үлкен дәлдікпен сипаттауға болады. Модельде нейронның ішкі және сыртқы кеңістігі арасындағы потенциалдар айырымына (трансмембраналы потенциал) байланысты мембрана арқылы иондарды өткізу немесе өткізбеу мүмкіндігіне қарай иондық арналардың динамикасын ескеруге болады.

Ходжкин-Хаксли математикалық моделін нейрондағы сигналдарды өндіретін алғашқы аяқталған модель деп есептесе болады. Ходжкин-Хаксли моделінің теңдеулер жүйесі келесі түрде болады [5] :

(1. )

V айнымалысы мембраналы потенциалды сипаттайды, ал ол потенциалдың өзгерісі мембрана арқылы ағатын тоқтардық қосындысы арқылы анықталады. Мембранада екі түрлі тоқтар болады, біріншісі иондық арналар тогы (натрийлік жәен калийлік), екіншісі кету тогы (хлор иондары) . Иондық арналардағы мембраналық потенциалға қатысты өткізгіштігінің өзгерісі m, n, h айнымалылары арқылы анықталды, ал олардың динамикасы үш дифференциалдық теңдеулер арқылы сипатталады. Осы теңдеулердің оң жақ бөлігіне α(V) және β(V) бейсызық функциялар кіреді. g _Na , g _K , g _l параметрлері сәйкесінше келетін арналардың максималды өткізгіштіктерін анықтайды, V _Na , V _K және V _l - мәндері Нернст [6] теңдеуі арқылы анықталатын және мембрананың екі бетіндегі иондар концентрациясына тәуелді болатын, сәйкесінше ион типіне келетін теңөлшемді потенциалдар.

Ходжкин-Хаксли моделінің динамикалық режимдері потенциал өндірілуінің биофизикалық механизмдері және трансмембраналық тоқтардың ағу көзқарасы бойынша, сонымен қатар бейсызық физика және бифуркациялық теория көзқарасы бойынша да жан - жақты және толық зерттелген. Берілген модель нақты және тиянақты модельдеуге сай келеді, бірақ өзінің есептеп шығару қиындықтарына байланысты, ол жасанды нейрондардың көп санынан тұратын нейрондық жүйелердегі қиын жүйелік әсерлерді модельдеу үшін аз қолданылады.

Айтылып кеткен модель иондық механимздерді түсіндіру үшін негіз болды. Иондық механизмдер жүйке жасушасындағы мембрананың орталық және қосымша бөліктеріндегі қозуына немесе тежелуіне қатысады. Осы модель негізінде үлкен нейрондық жүйелерді құру және жүйелердің радиотехникалық жүзеге асыруын мақсатында жүйке жасушаларының көптеген математикалық модельдері жасалған [7-8] .

Ары қарай модельдің қолданысын арттыру мақсатында теңдеулер жүйесінің бірінші теңдеуінен, I _exc және I _inh синаптикалық тоқтарды қоса бастады. Одан басқа, әсерлерді сипаттау және мәліметтерді аппроксимациялау үшін, тәжірбиелік потенциал - тәуелді қисықтардың пішінін өзгеруі және жаңа тоқтардың қосылуы бар модельдер жасалған. Ходжкин-Хаксли модельдерінің түрлендірілген және классикалық түрлері динамикалық жүйелер теориясы мен бифуркациялық анализ әдістерінің негізгі зерттеу тақырыбы болып саналды [9-10] . Аталған модельдің бірінші қарапайым етіп жасалған моделі ретінде 1961 ж. [11] ұсынылған ФитцХью-Нагумо моделі болып табылады. Модель құрамына оң кері байланыс арқылы өзінқоздыруды жүзеге асыратын, дифференциалдық теңдеудің оң жақ бөлігінде кубтық бейсызықтықты сипаттайтын мембраналық потенциал және қалпына келу айнымалылары кіреді. Қалпына келу айнымалысы дифференциалдық теңдеуде сызықты оң жақ бөлігіндегі теріс кері байланысты қамтамасыз ететін айнымалы болып табылады. Модель келесі теңдеулермен сипатталады:

\[{\frac{d V}{d t}}=V\cdot V^{3}\cdot\ w+I_{w},\]

(1. )

мұндағы, V - мембраналық потенциалдың динамикасын сипаттайтын айнымалы, кіріс тогы I , қалпына келу w айнымалысы және тәжірбиелік түрде анықталатын a және b параметрлері .

Жасалған модельдердің ішіндегі қызықтыларының бірі түрлендірілген ФитцХью-Нагумо [12] генератор моделі болып табылады. Ол Ходжкин-Хаксли моделінің қарапайым, әрі кең таралған нұсқасы ретінде жасалған. Бұл модель сепаратристік шектік көптүрлілігі бар. Олар сигналды нейрондар арасында байланыс үшін шекасты тербелістерге және шекүсті қоздыру импульстеріне бөледі. Сонымен қатар модель шекті жүйелерге сәйкес келетін бір уақытта интегративті жауап қайтарулары және осцилляторлық жүйелер сияқты резонанстік сипаттамалары болады. Басқаша айтқанда, ақпаратты жиіліктік және фаза кодтаудың және декодтаудың мүмкіндігі бар.

Түрлендірілген ФитцХью-Нагумо генератор моделінің авторлары қоздыру шегінен төмен болатын, кенеттен периодты тербелістер өндіретін модель ұсынды. Мұндай нейрондар бұлшық еттердің жұмыс істеуінің әмбебап ырғағын беру кезінде бас миы арқылы қозғалыс координациясының мәселелерін шеше алатын нейрон болып табылады. Бұл модель белгілі динамикалық жүйелер негізінде жасалған және төртінші ретті дифференциалдық теңдеулер жүйесімен сипатталады [13, 14] . Сурет 1. 1-де модельдің функционладық сұлбасы келтірілген.

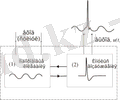
Сурет 1. 1. Қоздырылған элементтің шекасты тербелістері бар моделі. Функционалдық сұлба [14] .

Бірінші блок шекасты тербелістерді сипаттайды және қозудың жұмсақ режимі кезіндегі Ван дер Поль генераторы негізінде жасалады. Екінші блок импульстің пайда болуына жауап береді және ФитцХью-Нагумо қоздырылған элементі ретінде жүзеге асырылады. Блоктар арасында бейсызық байланысты орнатқанда, модель динамикасы келесі 4 - ретті жүйемен сипаттала алады:

\[\begin{array}{l}{{\mathrm{i}\ e_{\nu}\hat{\mathrm{k}}=f(u)-\nu-\enspace y;}}\\ {{\mathrm{i}\S=e_{2}(u+I),}}\\ {{\mathrm{i}\S=(g(1+a I+b u)-l x^{2})y-\omega_{o}^{2}x,}}\end{array}\]

(1. 4)

мұндағы, x және y айнымалылары бірінші блоктың динамикасын сипаттаса, ал u және v екінші блоктың динамикасын сипаттайды, f(u) - кубтық пішіндегі бейсызық функция, ε ₁ , ε ₂ - шамасы аз оң параметрлер, I - тұрақты сыртқы стимул, γ, β, l > 0, α < 0 - Ван дер Поль айнымалыларының динамикасын сипаттайтын және блоктар арасындағы байланысты көрсететін параметрлер.

Айта кетсек, модельдегі u айнымалының динамикасы нейронның мембраналы потенциалының сапалық эволюциясын көрсетеді, ал x, y, v айнымалылары - иондық тоқтардың динамикасын, I параметрі нейронның деполиризация деңгейін анықтайды. Жүйеде шамасы аз екі ε1, ε2 параметрлерді қосу блоктар арасындағы сипаттық уақыттық масштабтарды келістір үшін қажет (импульс ұзақтығы және шекасты тербелістердің периоды) . Модельде динамикалық қасиеттері әр түрлі екі бейсызық жүйелердің арасында байланыс орнатылғанын айта кеткен жөн. Блоктар арасында байланыс келесі түрде жүзеге асырылады: гармоникалық тербелістерге жақын бірінші блоктағы (x, y) екінші блоктағы тербелістерді u айнымалы арқылы күйін өзгертеді. Өз кезегінде шекасты тербелістердің амплитудасы мембраналық потенцил u мен сыртқы стимулға I қатысты тәуелді түрде өзгереді.

(а)

(а):

(б) (в)

(а):

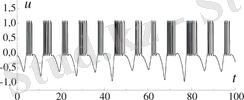
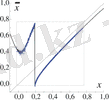
Сурет 1. 2. Модельдегі (1. 5) хаосты берсттық тербелістер

I=-0. 027. (а) Мембраналық потенциал эволюциясы. (б) ( x, u ) бетке проекциялағандағы фазалық траектория. (в) Хаостық аттракторға жауап беретін Пуанкаре көрінісі.

Модель блоктарының сипатттық уақыттық масштабтарының белгілі бір қатынасында тербелістер берсттық болып табылады. Берсттық тербелістер жүйелі түрде және хаостық болуы мүмкін. Сурет 1. 2-де хаостық тербелістердің уақыттық көрінісі және хаостық аттракторға сай келетін Пуанкаре көрінісі келтірілген.

1. 2 Жасанды нейрон торлары (ЖНТ) және олардың қолдануы

Интеллектуалды жүйелерді (SMART System) жасаудағы негізгі бағыттардың болып нейрон торлары табылады. Бүгінгі таңда жасанды нейрон торлары келісі мақсаттарда қолданылады [15-20] :

объекттерді, процестерді іріктеу (классификациялау) ;
бейнені тану/іріктеу/жіктеу/сараптау;
функцияны аппроксимациялау;
болжау;
оңтайландыру (оптимизация) мәселелерін шешу;
әлсіз детерминирленген ортада басқару мәселелерін шешу.

Көп жағдайда ЖНТ өзара байланысқан бірнеше жасанды нейрондар жүйесінен құралады. Жасанды нейрон биологиялық нейронның негізгі қасиеттерін қайталайды. Жасанды нейронның кірісіне көптеген сигналдар келіп түседі. Олардың әрқайсысы басқа нейронның шығысы болып табылады.

Жасанды нейрондар торының ең қарапайым моделі өлшенген сумматор болып табылады. Оның жалғыз шығысы бірнеше кірістері арқылы және салмақтар матрицасы арқылы анықталады:

\[y_{_{j}}=f(\sum_{i}w_{i j}x_{i}+w_{_{0}})\]

, (1. 6)

мұндағы,

\[{\mathit{V}}_{j}\]

- j - нейронның шығысы,

\[X_{i}\]

- i - нейронның кірісіндегі кіріс сигналы,

\[W_{i j}\]

- j -ші нейронның i - кірісіндегі синаптикалық салмақ,

\

- нейронның ығысу коэффициенті, ал f - белсендіру функциясы.

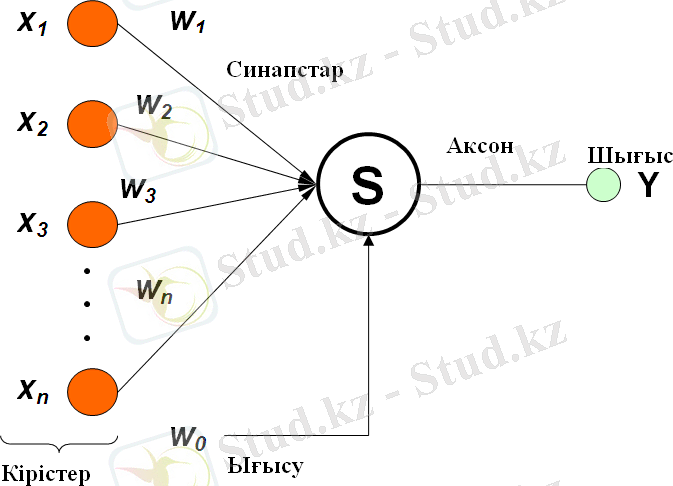
Сурет 1. 6. Қарапайым нейрон сұлбасы

Бұл суретте нейрондар векторы, олардың әрқайсысында кіріс мәліметтер векторы синапс салмақтарының векторына көбейтіліп жалғыз нейрон кірісіне беріледі, сонымен қатар, нейрон $x_{0}$ кірісіне $w_{0}$ бірлік кіріс салмағы беріледі. Бұл кіріс нейронда сезімталдылық шегін орнату үшін қажет. Нейрон шығысы өз күйінің функциясы болып табылады.

ЖНТ ғылым мен техниканың әр түрлі салаларында қолданыс табуда. Мысалы, жасанды зейінді оқыту тұрғысынан бейнені танудың, дискриминантты анализдің, іріктеудің және т. б. әдістерінің жеке жағдайы болып табылады. Ал математикалық тұрғыдан нейрон торларының бейімделуі (оқытылуы) - бейсызық оңтайландырудың (оптимизация) көппараметрлі есебі. Кибернетикада бейімделуші басқару және робототехникалық алгоритм ретінде қолданылады. Есептеуіш техника мен бағдарламалық бағытта нейрон торлары әсерлі параллелизмнің шешу әдісі ретінде қарастыруға болады. Жасанды зейін жасау бағытында да нейрон торлары табиғи зейінді мейлінше ұқсас етіп қалыптастыруда маңызы зор.

Атап өту керек болған негізгі жайт: нейрон торлары әдеттегі түсініктегідей бағдарланбайды, олар оқытылады. Оқытылу мүмкіндігінің болуы нейрон торларына дәстүрлі алгоритмдер алдында үлкен басымдылық береді. Техникалық тұрғыдан қарағанда, оқытылу дегеніміз нейрондар арасындағы байланыс коэффициетін табуды білдіреді. Оқытылу барысында нейрон торлары кіріс және шығыс мәліметтер арасындағы күрделі байланыстарды анықтап, оларды жинақтай алады. Яғни, нейрон торы сәтті оқытылған жағдайда, ол кіріс мәліметтің толық болмауы, бұрмалануы немесе шуылмен болғанына қарамастан дұрыс нәтиже қайтара алады.

Жалпы алғанда, нейрон торларын түрлі мәселелерді шешу барысында әр түрлі белгілеріне байланысты бөлуге болады:

Кіріс ақпараттың түріне байланысты жіктеу:

Аналогты нейрон торлары (ақпаратты нақты сандар түрінде қолданады) ;
Екілік нейрон торлары (екілік түрде белінген ақпаратты өңдейді) .

Оқытылу сипатына байланысты жіктеу:

Мұғаліммен оқытылу - нейрон торының шығыс мәлісеттер кеңістігі белгілі; Мұғалімсіз оқытылу - нейрон торлары шығыс мәліметтер кеңістігін тек кіріс мәліметтер негізінде қалыптастырады. Осындай торларды өздігінен ұйымдастырылатын деп аталады; Бекітумен оқытылу - сөгіс пен мақтау беретін жүйе арқылы оқыту.
Синапстарды баптау ерекшелігі бойынша жіктеу:Тұрақты байланысы бар торлар; Динамикалық байланысы бар торлар.
Байланыс сипаты бойынша жіктеу:Тікелей таралу торлары; Рекуррентті нейрон торлары; Радиалды-базисті; Өздігінен ұйымдастырылатын карталар.

1. 3 Динамикалық жүйелер

Динамикалық жүйелер дегеніміз кейбір, жеке қарастырғанда, қарапайым дифференциалдық теңдеулердің жүйесі (ҚДТ) үшін Коши есептерінде қарастырылатын, параметрдің уақыт бойынша тәуелділігін анықтауға байланысты есептер класын айтады. Динамикалық жүйелер деп

\[\hat{G}_{t}^{\scriptscriptstyle1}(t),\]

\[i=1,...N.\]

(1. 7)

тектес қарапайым дифференциалдық теңдеулер жүйесі болып саналады.

\[{f_{i}}\]

функциясы кез-келген

\[x_{i}(t)\]

тәуелді болуы мүмкін, яғни

\[{\dot{x}}(t)\]

векторлары, сондай-ақ одан басқа аргументтер жекелегенде t уақыт бойынша (осындай жағдайда теңдеулер динамикалық жүйесі автономды емес деп аталады) :

\[{\mathcal{R}}_{t}=f_{t}({\overset{.}{x}},t)\]

. (1. 8)

Көп жағдайда, динамикалық жүйелер теориясында t уақыты бойынша аргументіне анық түрде тәуелділік байқалмайтын автономды жүйелер қаралады (1. 7) .

Осыдан бөлек,

\[\ f_{i}\]

функциясының аргументі ретінде, тәжірибелік қызықты динамикалық жүйелердің көп бөлігіне тән, біз

\[{\frac{\mathbb{F}}{\hat{\theta}}}{\hat{\mathcal{I}}}.\]

векторымен белгілейтін әртүрлі параметрлер көп қатысады:

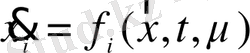. (1. 9)

Динамикалық жүйе параметрлік түрде осындай

\[\textstyle\int\!d\]

санынан бір, сонымен қатар екі немесе одан да көп болатын параметрлерден тәуелді болуы мүмкін. Жалпы жағдайда саны N-ге тең теңдеулерден бөлек, N бастапқы шарт қойылған болуы керек:

\[x_{i}(t)={\hat{a}}_{i}\]

. (1. 10)

Тәжірибеде,

\[{\dot{x}}(t)\]

- ның қарапайым шешімін іздеуден бөлек одан да маңызды, әрі қиын есептердің шешішім табу керек болады.

Көп кездесетін келесі мәселе:

\[{\dot{x}}(t)\]

-ның шешімі параметрлер немесе

\[{\frac{\mathbb{F}}{\hat{\theta}}}{\hat{\mathcal{I}}}.\]

параметрінің топтары өзгергенде не болады.

\[{\frac{\mathbb{F}}{\hat{\theta}}}{\hat{\mathcal{I}}}.\]

-дің өзгерісі кезінде шешім

\[{\frac{\mathbb{F}}{\hat{\theta}}}{\hat{\mathcal{I}}}.\]

-дің белгілі мәндеріне сәйкес танымастай сандық та, сапалық та жағынан өзгереді. Бұл байланыста

\[x_{i}(t)\]

функциясының құрылымын да білу емес, тек қана оның үлкен мәнді уақыттарда,

\[t~(\mathbb{S})~~\infty\]

болғандағы қасиетін білу қажет.

Есеп максималды түрінде кеңейюі мүмкін:

\[t~(\mathbb{S})~~\infty\]

болғанда еш шектеусіз бастапқы шартта шешім қандай болады. Демек, динамикалық жүйелерді зерттеу кезінде, тек жалғыз Коши есебінің шешімін ғана емес, сонымен қатар көптеген Коши есептерінің шешімдері болады екен.

Динамикалық жүйелер жайлы есептердің ерекшеліктерінен басқа, шешімді

\[{\dot{x}}(t)\]

графигі түрінде емес, фазалық кеңістікте салуға ыңғайлырақ болады. Егер біз N өлшемді кеңістікті қарастырсақ,

\[{\mathcal{X}}_{1}\left(t\right),{\mathcal{X}}_{2}\left(t\right)_{\gamma\circ\cdot\cdot\cdot\cdot}{\mathcal{X}}_{N}\left(t\right)\]

функцияларын әр координат остерінің бойына қоятын болсақ, онда фазалық кеңістік деп аталатын кеңістікті аламыз.

Мұндай жағдайларда

\[{\mathcal{X}}_{1}\left(t\right),{\mathcal{X}}_{2}\left(t\right)_{\gamma\circ\cdot\cdot\cdot\cdot}{\mathcal{X}}_{N}\left(t\right)\]

есептеу жағдайларында қалай байланысатындығын зерттейтін болғандықтан, уақыттан тәуелділік біркелкі параметрлік болып табылады. Бұдан кейбір ақпараттар, әдетте, жоғалып кетеді. Жеке етіп алғанда, біз

\[X_{i}\]

шешімінің t уақытпен динамикалық өзгерісін біле алмаймыз. Алайда, фазалық кеңістіктің графигінде бірнеше Коши есебінің шешімін есептеуге болады. Олардың әрбірі алғашқы шартпен анықталатын

\[{\dot{x}}(0)\]

алғашқы нүктесінде сәйкесінше қисық сызықпен беріледі.

Егер бар болғаны екі теңдеуден тұратын теңдеулер жүйесі қарастырылатын болса, онда N=2 және сәйкес келетін фазалық кеңістікте

\[x_{1}(t)\]

және

\[x_{2}(t)\]

шешімдері алынып, қойылатын қарапайым координаттық жазықтық болады. Егер теңдеулер саны N=3 болса, онда сәйкес келетін фазалық кеңістік үшөлшемнен тұратын кеңістік болып табылады. N>3 болған кезде, фазалық кеңістіктің көрінісі жоғалады. Осындай жағдайда фазалық кеңістіктің проекциясын жазықтыққа немесе үшөлшемді жазықтыққа құру қалыптасқан. Одан бөлек, қосымша Пуанкаре бейнесінің көрінісімен байланысты визуализациялау әдістері бар. Шектеулі емес бастапқы шарт пен кейінге қалдырылған фазалық жазықтық үшін алынған көптеген шешімдер динамикалық жүйенің фазалық портретін құрады. Есептеу жағынан қарағанда, фазалық портретті зерттеу есебі бастапқы шарт үшін ҚДТ шешімінің көшірмесіне қатты ұқсас болып келеді.

ҚДТ-дің шешімдерінің визуализациясы үшін фазалық портреттің маңыздылығын көрсете алатын мысал ретінде Бальтазар Ван дер Поль ұсынған осциллятордың классикалық модельдін қарастырайық:

\[{\frac{d^{2}x}{d t^{2}}}-\mu\left(1-\ x^{2}\right){\frac{d x}{d t}}+x=0.\]

(1. 11)

Келесі амалдарды қолданып, яғни дифференциалдық теңдеудің ретін төмендетсек, дифференциалдық теңдеулер жүйесін аламыз.

Келесі алмастыруды орындап:

\[y={\frac{d x}{d t}},\]

(1. 12)

осыдан бірінші ретті дифференциалдық теңдеулер жүйесін аламыз.

\[{\frac{d x}{d t}}=y,\]

\[{\frac{d y}{d t}}=\,\mu(1-\,x^{2}){\frac{d x}{d t}}-x,\]

(1. 13)

мұндағы, x-t уақытына тәуелді координата мәндері, µ - тербелістің сөнуін және бейсызықтығын көрсететін белгілі бір коэффициент. Сурет 1. 7-де көрстетілгендей

\[{\hat{\mathcal{I}}}{\hat{\mathcal{I}}}\]

= 0, 1 болған кезде, әр түрлі бастапқы шарттардан шыққан траекториялар фазалық кеңістіктегі шекті цикл деп аталатын тұйықталған қисыққа тартылады. Осыған байланысты x(t) және y(t) шешімдері автотербелістер деп аталатын осцилляциялар сипатына ие болады.

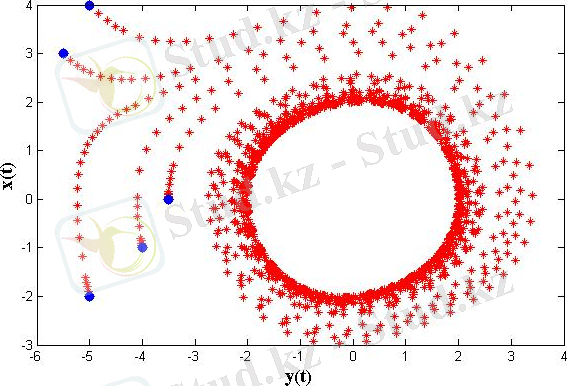
$C:\Users\Kuandyk\Desktop\Diss_Bekbolat\Graphics\VandPol.jpg$

Сурет 1. 7. Ван дер Поль осцилляторының µ = 0. 1 болғанда фазалық портреті

Жүйедегі µ шамасы аз болғанда периоды 2π болатын гармоникалық тербелістер пайда болады. Осы параметрдің шамасы үлкен мәндерінде тербелістер гармоникалық тербелістерге ұқсамайды, периоды 1. 614µ болытын релаксациялық тербелістер пайда болады.

Үлкен уақыт аралықтарындағы динамикалық жүйелердің өзгеру тәртібін зерттейік:

\[\widehat{\bf x_{\mathrm{r}}}=f_{i}({\dot{\bf x}},\alpha,{\dot{\mu}})\]

болғанда,

\[t\left(\mathbb{g}\right)\ \infty\]

. (1. 14)

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.