Синхронизация құбылысы

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

Синхронизация құбылысы

Синхронизация құбылысын 1665 жылы ұлы голландық физик Христиан Гюйгенс ашты. Ол екі маятникті сағатты бір қабырғаға жақын етіп іліп койғанда, біраз уақыттан кейін сағаттар толықтай синхронды қозғалатының байқаған. Ал сағаттарды бөлменің қарама қарсы қабырғаларға іліп қойғанда, синхронизация құбылысы байқалмады. Осы сағаттардың маятниктерінің тербелістерінің синхронизациясын, екеуінің бір-біріне қабырғанын көзге көрінбейтің вибрациясы арқылы әсер етенің түсіндіруге болатыны анық.

Синхронизация дегеніміз авторбермелі жүйелердің ритмдерің, арасындағы әлсіз өзара әрекеттесу арқылы реттеу болып табылады. Басқаша айтқанда, тербелістердің синхронизациясы деп өзара әрекеттесетің тербелмелі жүйелердің генерациялайтың жиілік, фаза немесе сигналдардың басқа да сипаттамаларының сәйкес келуін айтамыз.

Қарапайым жағдайда, бастапқыдан әртүрлі жиіліктер мен тәелсіз фазалы екі автотербелмелі жүйелер әлсіз байланысқан бола тұра, өздерінің ритмдерің сәйкестендіріп, бір жиілікте тербеле бастайды, оның үстіне осы екі осциляторладың фазалары арасында тұрақты қатынас пайда болады.

Ритм сипаттамалары: период және жиілік

Автотербелмелі жүйелер қарапайым, синусоидаға жақын және де қысқа импульстер сигнал қатарлары сияқты әр түрлі формалы ритмдерді ритмдерді көрсете алады. Осындай ритмдерді сипаттауды маятниктік сағат мысалында көрсетеік. Маятниктің тербелісі - периодты, және период T сағаттың басты сипаттамасы. Көбінесе ритмді бірлік уақыт ішіндегі тербеліс санымен немесе тербеліс жиілігімен сипаттау жеңіл болып келеді.

$f = \ \frac{1}{T}$

Тербелісті теориалық анализ кезінде бұрыштық жиілік $\omega = 2\pi f = 2\pi/T$ ретінде қолданған ыңғайлы.

Ритмдерді сәйкестендіру:фаза мен жиілік тусіру(ұстау)

Эксперименттер өзара әрекеттесу әлсіз болғанның өзінде де, екі маятниктік сағат синхрондалатының көрсетеді. Бұл дегеніміз, екі ұқсас емес сағат бөлек алынған кезде әртүрлі периодқа ие, ал егер арасында байланыс болғанда, өздерінің ритмдерің сәйкестендіреді және ортақ периодты тербелісті көрсете бастайды. Бұл құбылыс тусіру(ұстау) арқылы жиіліктерің сәйкестендіру деп аталады. Егер екі ұқсас емес, өздерінің жиіліктері бар осцилляторлар байланысса, онда олар ортақ жиілікпен тербеле бастауы мүмкін. Осцилляторлар синхрондалуы екі факторға тәуелді.

Байланыс күші

Бұл параметр өзара әрекеттесу қаншалықты әлсіз немесе күшті екенін сипаттайды. Маятниктік сағаттармен жасалған экспериментте ол күрделі түрде қабарғаның(балка(подвеса) ) қаншалықты қозғала алатынына тәуелді. Шынында, егер балка абсолютті қатан болса, онда маятниктер қозғалысы опора арқылы берілмейді, сәйкесінше сағаттар өзара әрекеттесе ете алмайды. Егер сағаттар өзара әрекеттеспесе, онда байланыс күші нолге тең. Егер балка қатан болмаса, онда бұнда өзара әрекеттесу орын алады

Автотербелмелі жүйелер

Автотербелмелі жүйелер ұғымын А. А. Андронов пен А. А. Витт енгізді. Дегенмен, Рэлей өзін-өзі қолдайтын және мәжбүр тербелістерді ажыратқан және де А. Пуанкаре шектік цикл ұғымын енгізген болғанымен, Андронов пен Витт қатаң математикалық әдістер мен физикалық идеяларды бірге қосты. Автотербелмелі жүйелер динамикалық жүйелер класының ішкі жиыны болып табылады.

Электрондық лампа негізіндегі радиожиіліктік генератор, маятниктік сағат, адам жүрегінің жиылуы және т. б. көптеген жүйелер сияқты әртүрлі осцилляторларда не ортақ ? егерде осы жүйелерді сыртқы ортадан оқшауласақ, онда олар өзінің ритмде тербелістерді генерациялауын жалғастыратын активті жүйе болып келуі, олардың негізгі универсалды қасиеті болып табылады. Бұл ритм толығымен жүйенің қасиеттерімен анықталады; ол жүйедегі дисспация орнын толтыратын, энергиянын ішкі көзі арқылы қамтамасыз етіледі. Осындай осциддяторлар автономды деп аталады. Олар физика мен бейсызық динамикада автотербелмелі жүйелер атымен белгілі, бейсызық моделдер класымен сипатталады.

Мысал ретінде, шығысында периодты процессты генерациялайтын осцилляторды қарастырсақ. $x(t)$ деп процесс мәнін белгілейік. Егер осциллятордың белгілі уақыт мезетіндегі күйін сипаттайтын болсақ, онда $x$ мәні білу бізге жеткіліксіз болып келеді. Себебі $x$ процессі уақыт өте өсуіде кемуіде мүмкін. Бұдан шығатыны, жүйе күйін анықтау үшін кемінде екі айнымалы болуы керек. Маятниктік сағат үшін бүл айнымалылар, маятниктің вертикалдан ауытқу бұрышы және бұрыштық жылдамдық ретінде қарастырса болады. Енді жүйенің күйін екі өлшемнің $(x, \ y)$ уақыт мезетіндегі эволюциясымен толық сипатталына алады ( 1 - сурет) . Бұл айнымалылар фазалық кеңістіктің координаттары, ал $y(t)$ -тің $x(t)$ -қа тәуелділігі жүйенің фазалық портреті деп аталады. Егер тербеліс периодты болса, яғни $T$ период сайын қайталанса, $x(t)$ шектік цикл деп аталатын, фазалық жазықтықтағы тұйық қисыққа сәйкес келеді (2-сурет) .

: 1-сурет. периодты тербеліс фазалық кеңістікте түйық қисықпен көрсетілген:

x(t)

және

x(t + T)

эквивалентті күйлері осы қисықтағы бір нүктеге сәйкес келеді. Керісінше,

x(t)

бірдей күйлерімен әр түрлі болады, егерде екінші координатты ескерсек.

: 2-сурет. (a) фазалық жазықтықтағы тұйық қисық өзінің айналасындағы барлық траекторияларды тарту себебіне байланысты шектік цикл деп аталады. Осы траекториялар (b) уақытқа тәуелді көрсетілген.

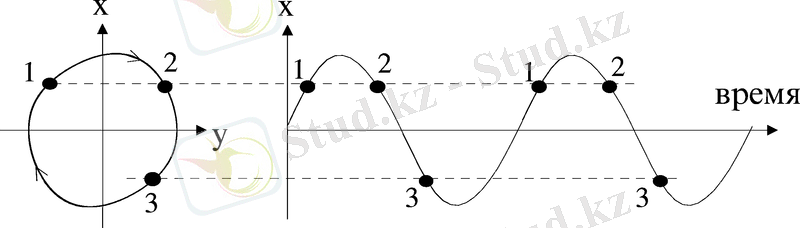
«Шектік цикл» терминінің шығуының түсіндіру ушін, ол фазалық жазықтықта басқа барлық траекториялардан немен ерекшеленетін тауып көрейік. Бұл мақсат үшін, цикл аймағындағы траектория жүрісін қарастырайық. Басқаша айтқанда, егер нүктені шектік циклдан итеріп жіберсек, не болатының көрейік. Бастапқы физикалық (немесе механикалық, биологиялық және т. б. ) жүйеге бұл дегеніміз, оның периодтық қозғалысын қалайда бұзу болып табылады. Біз автотербелмелі жүйелердің маңызды қасиетіне келдік: олардың тербелістерің бұзғаннан кейін жүйе озінің ритмін қалпына келтіреді, яғни фазалық нүкте шектік циклға қайтып келеді. Бұл қасиет, автотербеліс бастапқы шарттарға немесе жүйедегі қозғалыстың қалай пайда болғанына тәуелді емес екенін білдіреді. Фазалық жазықтық көрінісінде бұл біз фазалық нүктені басында жазықтыққа орналастыруға сәйкес келеді. 2 суреттен барлық траекториялардың циклға ұмтылысын көріп тұрмыз. Демек, өтпелі процесстен кейін, жүйеде фазалық нүктенің шектік цикл бойымен қозғалысына сәйкес, стационарлы тербеліс орнатылады.

Қорытындылай келе, автотербелісті фазалық кеңістіекте бейнесі-шектік цикл арқылы сипаттауға болады. Цикл формасы, сәйкесінше, тербеліс формасыда толығымен жүйенің ішкі параметрлерімен анықталады. Егер тербеліс формасы бойынша синусоидаға жақын болса, онда бұндай осциллятор квазисызықты (квазигармоникалық) деп аталады. Бұл жағдайда шекктік цикл щенбер ретінде көрсетілуі мүмкін.

Квазисызықты осциллятордың фаза мен амплитудасы

Квазисызықты осциллятордың шектік циклы шеңберге жақын, ал тербелістері синусоидалық, $x(t) = Asin(\omega_{0}t + \ \varphi_{0})$ , деп есептеуге болады. Мұндағы $\omega_{0}$ бұрыштық жиілікті білдіреді. Тербеліс интенсивтілігі олардың $A$ амплитудамен анықталады , ал $\varphi(t) = \ \omega_{0}t + \ \varphi_{0}\$ шамасы фаза деп аталады (3 сурет) .

: 3 - сурет. фазаны анықтау. Периодтық тербелістің фазасы уақыт бойынша біркелкі өседі және әр период сайын

2\pi

-ға үлкейеді.

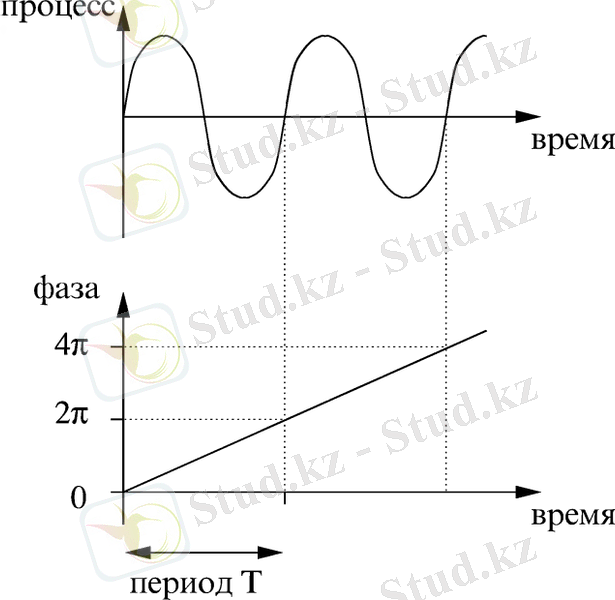
Тербеліс фазасы $\varphi(t)$ шектеусіз өседі, бірақ синус - периодтық функция болғандықтан, $sin\varphi = sin(\varphi\ + 2\pi)$ , онда $2\pi$ айырмашылы бар екі фаза бір физикалық күйге сәйкес келеді. Кейде ыңғайлы болу үшін щенберде (0 ден $2\pi$ -ге дейін) анықталатын циклдық фазаны қарастырады.

$\varphi_{0}$ - бастапқы фаза деп аталатын мүше болып келеді. Біз автотербелмелі жүйелер қосылған кезде, біраз өтпелі процесстен кейін, ол өзінің бастапқы күйіне тәуелсіз шектік циклға шығатының білеміз. Бұл тербеліс амплитудасы бастапқы шарттарға тәуелсіз екенің білдіреді.

Бастапқы фаза $\varphi_{0}$ , керісінше, соңғы күйге өтуіне тәуелді және де еркін бола алады, сәйкесінше, $\varphi_{0}$ барлық мәндері эквивалентті. Шынында, егерде біз тек орнатылған, стационарлы тербелісті қарастырсақ, онда біз бастапқы фазаны басқа уақыт есептеу нүктесін таңдау арқылы өзгерте аламыз.

Квазисызықты автотербеліске әлсіз әрекеттесу

Жоғарғы бөлімде біз автотербелмелі жүйелер туралы айтып кеттік. Енді біз әлсіз сыртқы әрекеттесу кезінде олармен не болатынын қарастырамыз. Мысал ретінде маятнигі магниттік материалдан жасалған сағат алып, оны айнымалы токпен қоректенетін электромагниттің жанына орналастырайық. Бұл жағдайда сағаттың автотербелісі әлсіз айнымалы магниттік өріспен ауытқиды.

Қарапайым көрсету үшін, автотербеліс квазисызықты, $x(t) = Asin(\omega_{0}t + \ \varphi_{0})$ , ал сыртқы күш - $\omega$ жиілігі бар гармоника, $\varepsilon cos(\omega t + \ {\overline{\varphi}}_{e})$ , мұндағы $\varphi_{e}(t) = \ \omega t + \ {\overline{\varphi}}_{e}$ - күш фазасы, ал $\varepsilon$ - оның амплитудасы болғандағы жағдайдан бастаймыз. Күш жиілігі $\omega$ жалпы жағдайда автотербеліс жиілігі $\omega_{0}$ - ден өзгеше, сәйкесінше соңғысы автономды жиілік деп атаймыз. Жиіліктер арасындағы айырым $\omega - \ \omega_{0}$ бұзу(расстройка) деп аталады. Жоғарыда айтылып кеткендей, амплитуда тұрақты, ал фаза нейтралды (тұрақты да, тұрақсыз емес) . Сондықтан әлсіз күш тек фазаны өзгерте алады (4 сурет) .

: 4-сурет. шектік циклдағы нүкте тұрақтылығы. (a) циклға перпендикулярлы бағытта нүкте тұрақты күйде орналасқан, амплитуда ауытқуы жылдам өшіп, тұрақты A мәнге ұмтылады. (b) цикл бойындағы фаза бойынша ауытқу өспейді де кемімейді. Фазаның тұрақты өсуі, бөлшектің көлбеу жазықтықпен сырғанауымен көрсетілуі мүмкін. Екі осындай бөлшек, ауытқымаған және ауытқыған фазаларға (● және ○ символдары) сәйкес, бір біріне қатысты тұрақты кідіріспен (задержка) сырғып келед. (c) айналмалы санау жүйесінде фаза тұрақты. Бұл бөлшектің горизонтальды жазықтықта орналасқанына сәйкес келеді. Үзік-үзік сызық фазаның

2\pi

-нің периодты айнымалы екенің көрсетеді.

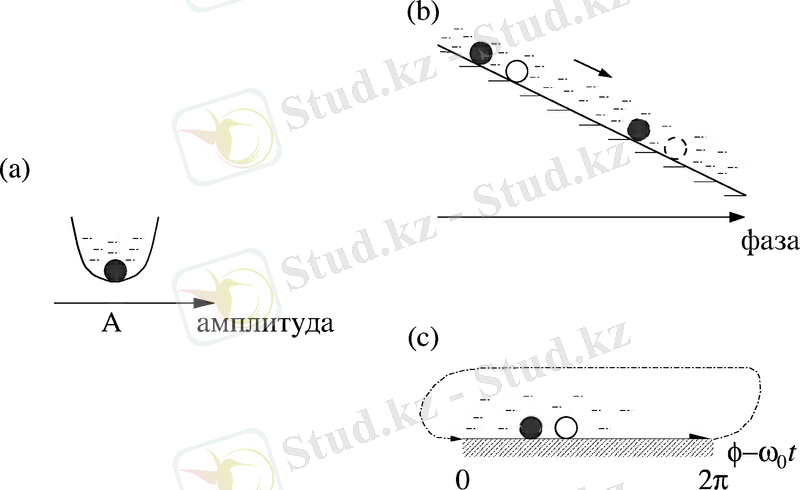
Бұзу(расстройка) болмағанда, $\omega_{0} = \ \omega$ , фазалық нүкте айналмалы жүйеде тыныштықта тұр; бұны бөлшектің горизонтальдық жазықтықта тыныш тұрғаны ретінде көрсетсе болады (4с-сурет) . Нольдік емес бұзу(расстройка), $\omega_{0} \neq \ \omega$ , кезіндегі фаза айырымының $\varphi - \varphi_{е}$ біркелкі өсуі немесе кемуін бөлшектің көлбеу жазықтықпен төмен сырғанауы ретінде қарастырса болады (4b-сурет) ; бұл жағдайда бөлшектің көлбеу потенциалда қозғалысы жиі айтылады. Бұл жағдайдын барлығы сыртқы күш нольге тең ( $\varepsilon = 0$ ) болған кезге сәйкес.

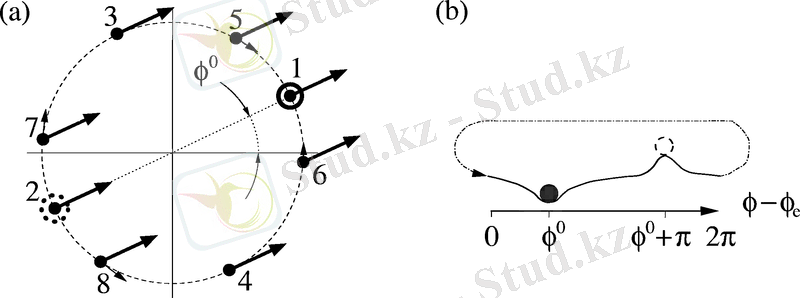
Енді сыртқы күшті қоссақ, яғни $\varepsilon \neq 0$ . Санау жүйесінде $\omega$ бұрыштық жылдамдықпен айналатын, $\omega$ жиілігімен осциллациялайтын $\varepsilon cos(\omega t + \ {\overline{\varphi}}_{e})$ күш, $\varphi^{0}$ әлдебір бұрышымен әсер ететін, $\varepsilon$ тұрақты ұзындық векторымен көрсетіледі. Күштін циклдегі фазалық нүктеге әсер нәтижесі $\varphi - \varphi_{е}$ фазалар айырымына тәуелді (5-сурет) . Шынында, 1 және 2 нүктесінде күш +фазасын жылжыта алмайды. 3 және 4 нүктелерінде әсер максималды, ал 5 - 8 нүктелерінде аралық(промежуточный ) эффект байқалады. Кейбір нүктелерде күш сағат тілі бағыты бойнша, ал басқаларында керісінше әсер етеді. Көріп тұрғандай, 1 және 2 нүктелері тепе-теңдіктің тұрақты және тұрақсыз күйіне жауап береді (5a - сурет) . Жеңіл бөлшектің жазықтықта қозғалу аналогиясын қолдана отырып, күш жазықтықтың қисаюына алып келетінің айтса болады, әрі минимум және максимум тепе-теңдіктің тұрақты және тұрақсыз күйге сәйкес келеді (5b-сурет) .

: 5-сурет. (a) Әлсіз сыртқы күш шектік циклда амплитуданы өзгерте алмайды, бірақ автотербелестің фазасын жылжыта алады. Күштің әсер етуі фазалар айырымына

\varphi - \varphi_{е}

тәуелді: 3 және 4 нүктелерінде әсер максималды, ал 1 және 2 нүктелерінде күш радиус бойынша әсер етеді және сондықтан цикл бойында фазалық нүктені жылжытпайды. 1 және 2 нүктелері тұрақты және тұрақсыз күйлерге сәйкес келеді. (b) суретте тепе-теңдік күйлері көрсетілген.

Глобальды байланысқан осцилляторлар ансамблі

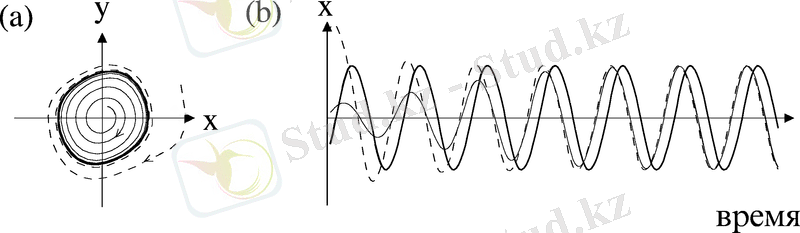
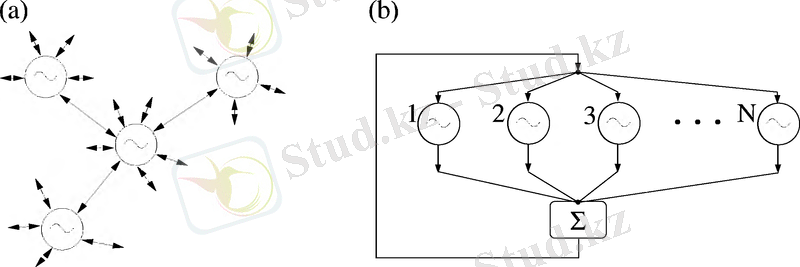
Бұл бөлімде біз әр елементтері басқаларының барлығымен өзара әрекеттесетің үлкен осцилляторлар ансамбліндегі синхронизация құбылысын зерттейміз (6a-сурет) . Бұндай байланысты әдетте глобальды немесе « әрқайсысы әрқасысымен (каждый с каждым) » типті байланыс деп атайды.

: 6-сурет. (a) Әр осциллятор үлкен популяцияда басқаларымен өзара әрекеттеседі. (b) эквивалентті көрінісі: ансаблдің әр элементі, барлық элементтермен жасалатын орта өріс әсеріне шалдығады.

Коллективті синхрондалу құбылысын түсіну үшін біз ұқсас емес осцилляторлар ансамблін қарастыру керекпіз. Біз бұзу(расстройка) өте үлкен болағанда жүйе синхрондалатының білеміз. Демек, синхронизация популяцияның барлық немесе оның үлкен бөлігін қамтуы мүмкін.

Қосалқы қадам ретінде 6a-суретті эквивалентті түрде 6b-суретте көрсетілгендей етіп сызып аламыз. Бұл жерде біз осцилляторға басқа осцилляторлар жағынан әсер ететін күштің қосындысын, толықтай ансамбль жағынан әсер ететін бір күшпен ауыстырдық. Шынында, әр осцилляторға ансамблдегі барлық осциллятордың тербелістерінің қосындысы пропорционалды екенін айтса болады.

Барлық осцилляторлардың жиілігі бір-біріне жақын болғанда және ортақ күш әсер еткенд, ол күш көп осцилляторларды қармып алуы мүмкін екенін білеміз. Бұндағы мәселе, глобальды байланыс болғанда, бұл күш немесе орта өріс бастапқыда белгіленбеген, ол ансамбльдегі өзара әрекеттесуден пайда болады. Бұл күш, жүйе синхрондалған ба екенің анықтайды, бірақ өзі олардың тербелістерінен тәуелді.

Бұл күштің пайда болуын түсіндіру үшін, алдымен орта өріс нольге тең деп есептейік. Онда ансамбльдың барлық элементтері тәуелсіз осцилляциялайды, және де олардың орта өріске үлесі компенсацияланады. Тіпті егер де бұл тербелістердің жиіліктері ұқсас болғанымен, фазалары тәуелсіз, ансамблдің барлық элементтері шығыстарынан орташасы, жалғыз осциллятор амплитудасымен салыстырғанда аз. Осылайша, нөлдік өріс кезіне асинхронды күй сәйкес келеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.