Логика алгебрасы

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 2 бет
Таңдаулыға:

2. Буль алгебра ұғымы. 3. Буль алгебрасының негізгі қасиеттері. Логика алгебра (Бульдік алгебра) - бұл ағылшын математигі Джордж Бульдің атымен аталатын ХІХ ғасырда пайда болған математика бөлімі. Басында буль алгебрасының ешқандай практикалық маңызы болған жоқ. Бірақ ХХ ғасырда ол әр түрлі электрондық сұлбаларды дайындауда және қызмет атқаруын сипаттауда үлкен маңызы болды. Логика алгебрасының заңдары мен аппараты компьютердің әр түрлі бөліктерін (жады, процессор) жобалауда пайдалана бастады. Әрине бұл осы ғылымды қолданудағы жалғыз сала емес. Логика алгебрасы нені білдіреді? Біріншіден, алгебралық әдістердің көмегімен күрделі логикалық айтылымдардың ақиқаттылығын немесе жалған екенін орнататын әдістерді қарастырады. Екіншіден, бұл күрделі логикалық айтылым буль алгебрасында есептеу нәтижесі не ақиқат, не жалған (1, немесе 0) болуы мүмкін функциямен сипатталады. Бұл жерде функция аргументтері (қарапайм айтылымдар) де тек қана 0 немесе 1 мәндерін қабылдай алады. Сонымен Буль алгебрасы деп екі бинарлық операциядан (конъюнкция, дизъюнкция), унарлық операциядан (теріске шығару) және екі ерекшелінген (0 немесе Жалған және 1 немесе Ақиқат) элементтерінен тұратын бос емес жиынды айтамыз. Қарапайым логикалық айтылым дегеніміз не? Мысал негізінде түсіндірейік. Екі сөйлемді қарастырамыз: «Екі бірден артық», «3, 14 - бүтін сан». Бірінші жаңдайда айтылым нәтижесі ақиқат, екінші жағдайда - жалған. Логикалық операциялар. Дизъюнкция, конъюнкция және терістеу. Күрделі айтылымдарға мысалдар: «осы аптада, немесе келесі аптады күн суытады», «мен сабақ оқып болғаннан кейін қыдырамын», «5 пен 7 өз ара тең емес» т. т. міне, осындай күнделікті өмірде кездесетін оқиғаларды математика аппаратына салып қатаң ережелер енгізіп бір мәнді нәтиже алатындай іске асырылатын болды. Жоғарыда келтірілген мысалдардағы «және», «немесе» одақтары логикалық амалдарға түрлендірілді. Логика алгебрасы логикалық операциялардың жиынын құрайды. Соның ішінде, әсіресе үш операцияға ерекше көңіл бөлінеді: конъюнкция (ЖӘНЕ), дизъюнкция (НЕМЕСЕ) және терістеу (ЕМЕС) . 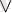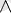Көбінесе конъюнкцияны $\lor$ немесе & , дизъюнкцияны - $\land$ немесе , ал терістеуді - $\neg$ немесе айнымалының үстінен сызықшақою арқылы белгіленеді. Басқа операциялар осы үш операция арқылы өрнектеледі.

Конъюнкцияда барлық қарапайым өрнек ақиқат болған жағдайда ғана күрделі өрнектің ақиқаттылығы алынады. Қалған жағдайда күрделі өрнек жалған болады.

Дизъюнкцияда қарастырып отырған күрделі өрнекке енетін бір немесе екі қарапайым өрнек ақиқат болған жағдайда күрделі өрнек ақиқат болады. Кей жағдайда күрделі өрнек үш немесе одан да көп қарапайым өрнектен тұруы мүмкін. Бұл жағдайда бір қарапайым өрнектің ақиқаттығы жеткілікті, сол кезде барлық айтылым ақиқат болады.

Терістеу - бір қарапайым өрнекке қатысты немесе күрделі өрнектің нәтижесіне қатысты орындалатындықтан унарлық операция болып табылады. Теріске шығару нәтижесінде бастапқы өрнекке қарама-қарсы жаңа айтылым алынады.

Логикалық операцияларды бастапқы қарапайым айтылымдардың әр түрлі мәндеріндегі күрделі айтылымдардың есептеулерінің нәтижелерін бейнелейтін ақиқаттылық кестесі деп аталатын кестемен симаттаған ыңғайлы. (Қарапайым айтылымдар айнымалылар арқылы белгіленеді, мысалы А және В)

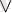A $\lor$ B

A: False

B: false

AB: false

A: True

B: false

AB: false

A: False

B: true

AB: false

A: True

B: true

AB: true

Конъюнкция. Конъюнкция үшін ақиқаттылық кестесі :

Қарапайымдылық үшін 0 және 1 цифрларын алыңыздар, ал 'ЖӘНЕ' - логикалық көбейту болғандықтан көбейтіп тексеріңіздер.

Дизъюнкция. Дизъюнкция үшін ақиқаттылық кестесі :

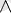A $\land$ B

A: False

B: false

AB: false

A: True

B: false

AB: true

A: False

B: true

AB: true

A: True

B: true

AB: true

Бұл жерде де түсінікті болу үшін цифрларды пайдаланыңыздар. 1+0 нәтижесі 1 болады, ол TRUE. Логикалық «Және» кезінде көбейту амалы орындалса «НЕМЕСЕ» жағдайында қосылады. Бұл ең қарапайым логикалық операция.

Қосжақтылық принципі.

Буль алгебрасында қосалқы тұжырымдар бар, олар не бір мезгілде ақиқат, не бір мезгілде жалған болады. Айталық, қандай да бір буль алгебрасындағы ақиқат формулада барлық конъюнкцияны дизъюнкцияға, 0-ді1-ге, ≤ таңбасын > таңбасына және керісінше ауыстырса онда осы буль алгебрасында ақиқат формула алынады.

Буль алгебрасының берілуі

Кез келген ақырлы буль алгебрасының элементтерінің саны екінің дәрежесі арқылы беріледі.

Буль функциялары

х айнымалысы тек қана 0 және 1 екі мәнін қабылдаса, онда х айнымалысы буль айнымалысы деп аталады. Түсіндіру мысалы ретінде қабырғада орналасатын екі жағдайы бар электр жарығын ажыратқышты қарастыруға болады. Бұл жерде 1 ауыстырғыштың жоғары қосылған жағдайы, 0-төмен орналасқан жағдайы.

Егер f(x ₁ , x ₂ , …, x _n ) функциясының барлық аргументтері бульдік болса, ал функцияның өзі тек қана 0 және 1 екі мәндерін қабылдаса, онда ол буль (немесе логикалық функция, немесе логика алгебрасының функциясы, немесе ауыстырғаш функция) функциясы деп аталады.

Буль функциясының берілу тәсілдері:

Буль функциясы да математика курсындағы функциялар сияқты тәсілдермен беріледі::

кестелік;
графикалық;
аналитикалық.

Компьютердің логикалық негіздері

ЭЕМ жұмысын логика алгебрасын сипаттайтын әр түрлі құрылғылар пайдаланылады. Осындай құрылғыларға ауыстырғыштар, триггерлер, қосындылауыштар (сумматор) жатады.

Сонымен қатар, бульдік алгебра мен компьютердің арасын ЭЕМ-да пайдаланылатын санау жүйесі байланыстырады. Ол белгілі екілік санау жүйесі. Сондықтан, компьютер компьютер құрылғыларында сандар мен қатар логикалық айнымалыларды да сақтауға және түрлендіруге болады.

Ауыстырғыш сұлбалар ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.